人教版七年级数学课件:6.1.1算术平方根课件(共20张PPT)
文档属性
| 名称 | 人教版七年级数学课件:6.1.1算术平方根课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 21:05:09 | ||
图片预览








文档简介
(共20张PPT)
6.1
平方根
细心,动脑,方法!
(第一课时)
教学目标:
1.了解算术平方根的概念,会用根号表示正
数的算术平方根,并了解算术平方根的非负性。
2.了解开方与乘方互为逆运算,会用平方运算求某些非负数的算术平方根。
问题1、旧知回顾——练一练
4
4
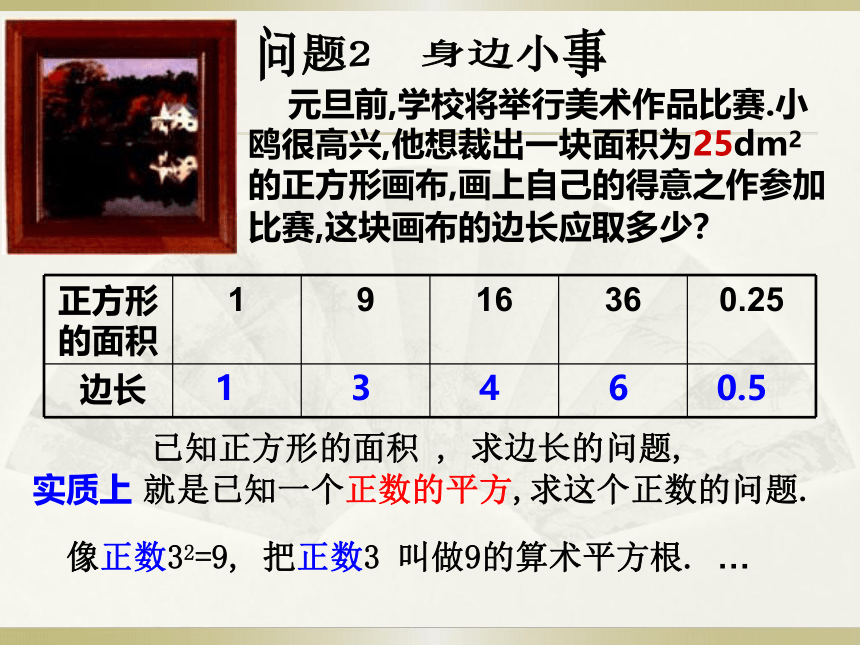
元旦前,学校将举行美术作品比赛.小鸥很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块画布的边长应取多少?
正方形的面积
1
9
16
36
0.25
边长
已知正方形的面积
,
求边长的问题,
实质上
就是已知一个正数的平方,求这个正数的问题.
1
3
4
6
0.5
像正数32=9,
把正数3
叫做9的算术平方根.
…
定义
一般地,如果一个正数
x
的平方等于
a(x2
=
a),
那么这个正数
x
就叫做
a
的
算术平方根
a
的算术平方根记作
读作
“
根号a
”
根号
被开方数
0的算术平方根等于0
如102
=
100
则100的算术平方根
算术平方根的性质
正数的算术平方根为正数,
0
有一个算术平方根——
0
,
负数没有算术平方根。
算术平方根具有双重非负性
求一个数的算数平方根与求一个正数的平方恰好是互逆的两个运算。
例1
求下列各数的算术平方根:
(1)900;(2)1;(3)
;(4)14.
解:(1)
因为302=900,所以900的算术平方根是30,
即
;
(2)因为12=1,所以1的算术平方根是1,即
;
(3)因为
,所以
的算术平方根是
,
即
;
(4)14的算术平方根是
.
在求a的算数平方根时,若a是有理数的平方,则a的算数平方根就不带根号;若a不是有理数的平方,则a的算数平方根就带根号,如
算数平方根是它本身的数只有0和1.
用含“
”的式子表示下列各数的算数平方根,并求出来。
学以致用
121
,
81
,49,36,0.81
规律:
被开方数越大,对应的算数平方根也越大。
11
~
20
的平方表
n
n2
n
n2
11
121
16
256
12
144
17
289
13
169
18
324
14
196
19
361
15
225
20
400
学以致用
带分数一般要化成假分数后再求它的算数平方根。
式子
的两层含义:
(1)
a≥0
;
(2)
≥0
.
训练(二)
细细辨别
若式子
在有理数范围内有意义,则x的取值范围是多少?
学以致用
小结:
财富大统计
1.谈谈你的收获……
2.从知识的角度讲,你还有哪些疑问?
(1)算术平方根的概念,式子
中的双重非负性:
一是a≥0,
二是
≥0.
(2)算术平方根的性质:
一个正数的算术平方根是一个正数;
0的算术平方根是0;
负数没有算术平方根.
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
作业:
(1)教科书P47
习题6.1的第1,2题.
(2)导学案P23
感谢各位领导、老师莅临
欢迎指正
6.1
平方根
细心,动脑,方法!
(第一课时)
教学目标:
1.了解算术平方根的概念,会用根号表示正
数的算术平方根,并了解算术平方根的非负性。
2.了解开方与乘方互为逆运算,会用平方运算求某些非负数的算术平方根。
问题1、旧知回顾——练一练
4
4
元旦前,学校将举行美术作品比赛.小鸥很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块画布的边长应取多少?
正方形的面积
1
9
16
36
0.25
边长
已知正方形的面积
,
求边长的问题,
实质上
就是已知一个正数的平方,求这个正数的问题.
1
3
4
6
0.5
像正数32=9,
把正数3
叫做9的算术平方根.
…
定义
一般地,如果一个正数
x
的平方等于
a(x2
=
a),
那么这个正数
x
就叫做
a
的
算术平方根
a
的算术平方根记作
读作
“
根号a
”
根号
被开方数
0的算术平方根等于0
如102
=
100
则100的算术平方根
算术平方根的性质
正数的算术平方根为正数,
0
有一个算术平方根——
0
,
负数没有算术平方根。
算术平方根具有双重非负性
求一个数的算数平方根与求一个正数的平方恰好是互逆的两个运算。
例1
求下列各数的算术平方根:
(1)900;(2)1;(3)
;(4)14.
解:(1)
因为302=900,所以900的算术平方根是30,
即
;
(2)因为12=1,所以1的算术平方根是1,即
;
(3)因为
,所以
的算术平方根是
,
即
;
(4)14的算术平方根是
.
在求a的算数平方根时,若a是有理数的平方,则a的算数平方根就不带根号;若a不是有理数的平方,则a的算数平方根就带根号,如
算数平方根是它本身的数只有0和1.
用含“
”的式子表示下列各数的算数平方根,并求出来。
学以致用
121
,
81
,49,36,0.81
规律:
被开方数越大,对应的算数平方根也越大。
11
~
20
的平方表
n
n2
n
n2
11
121
16
256
12
144
17
289
13
169
18
324
14
196
19
361
15
225
20
400
学以致用
带分数一般要化成假分数后再求它的算数平方根。
式子
的两层含义:
(1)
a≥0
;
(2)
≥0
.
训练(二)
细细辨别
若式子
在有理数范围内有意义,则x的取值范围是多少?
学以致用
小结:
财富大统计
1.谈谈你的收获……
2.从知识的角度讲,你还有哪些疑问?
(1)算术平方根的概念,式子
中的双重非负性:
一是a≥0,
二是
≥0.
(2)算术平方根的性质:
一个正数的算术平方根是一个正数;
0的算术平方根是0;
负数没有算术平方根.
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
作业:
(1)教科书P47
习题6.1的第1,2题.
(2)导学案P23
感谢各位领导、老师莅临
欢迎指正
