2020—2021年人教版数学七年下册 第7章 平面直角坐标系——平面直角坐标系中图形面积的求法 总结课件(共32张)
文档属性
| 名称 | 2020—2021年人教版数学七年下册 第7章 平面直角坐标系——平面直角坐标系中图形面积的求法 总结课件(共32张) |  | |
| 格式 | zip | ||
| 文件大小 | 547.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 08:54:56 | ||
图片预览



文档简介
(共32张PPT)
平面直角坐标系中图形面积的求法
在平面直角坐标系中描出下列各点,并求出线段的长度.
(1)若A(-1,0),B(5,0),则线段AB的长为____
(2)若C(0,3),D(0,-2),则线段CD的长为_____
(3)若E(-1,3),F(3,3),则线段EF的长为_____
(4)若M(-2,4),N(-2,-1),则线段MN的长为___
6
4
5
5
你发现了什么规律?
预备知识
预备知识
P(ɑ,b)
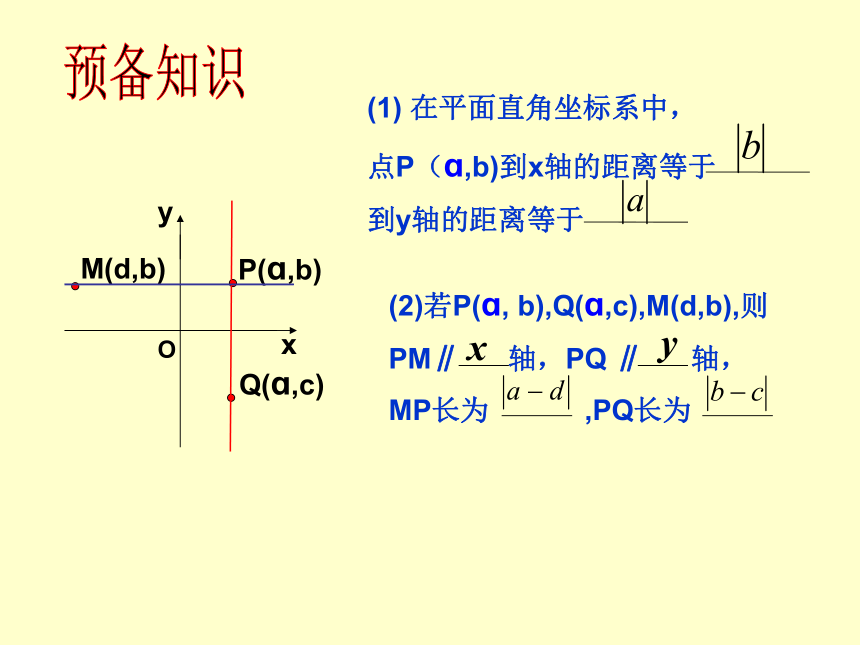
在平面直角坐标系中,
点P(ɑ,b)到x轴的距离等于
到y轴的距离等于
M(d,b)
Q(ɑ,c)
(2)若P(ɑ,
b),Q(ɑ,c),M(d,b),则
PM∥
轴,PQ
∥
轴,
MP长为
,PQ长为
x
y
x
y
O
二、探究规律
1.如图所示,△AOB的面积是
.
6
B(3,0)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
?
? A(0,4)
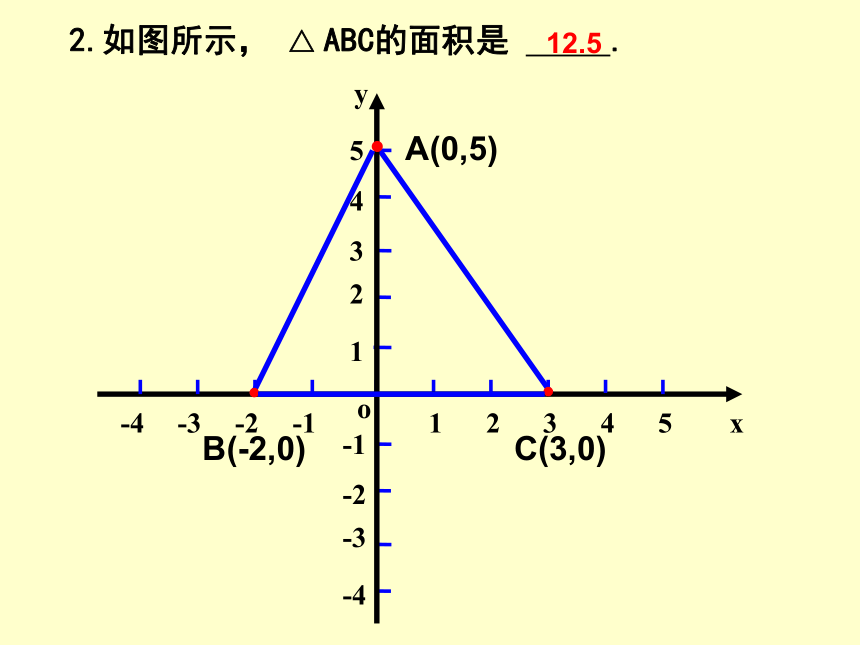
2.如图所示,
△
ABC的面积是
.
C(3,0)
B(-2,0)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
?
?
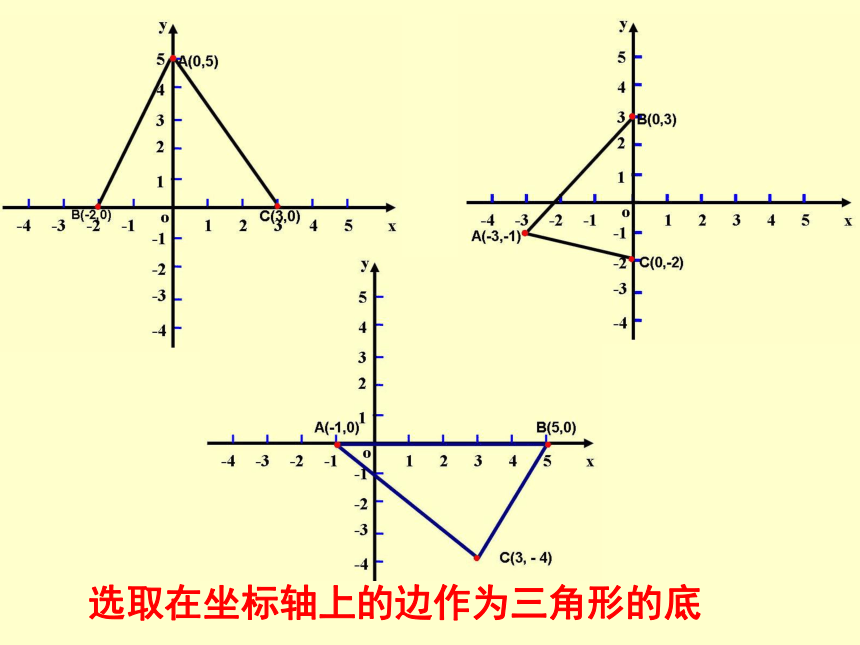
A(0,5)
12.5
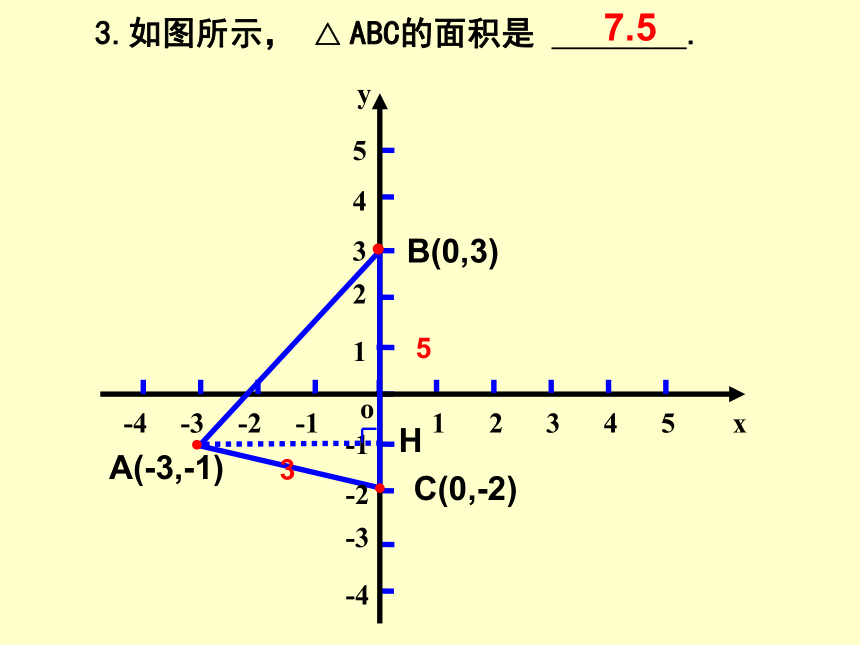
3.如图所示,
△
ABC的面积是
.
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
H
7.5
?
C(0,-2)
A(-3,-1)
?
?
B(0,3)
3
5
B(5,0)
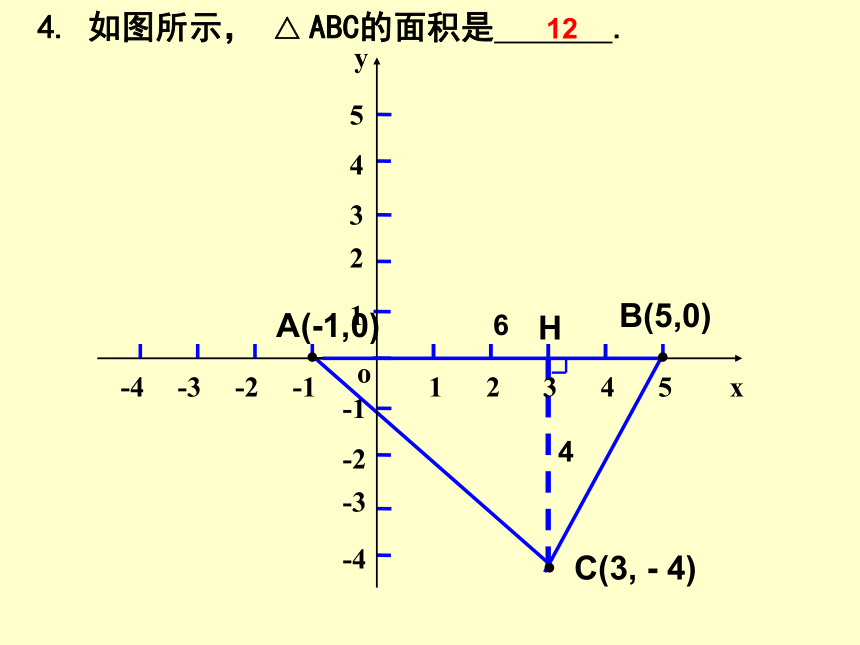
4.
如图所示,
△
ABC的面积是
.
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
C(3,
-
4)
H
A(-1,0)
?
?
12
6
4
选取在坐标轴上的边作为三角形的底
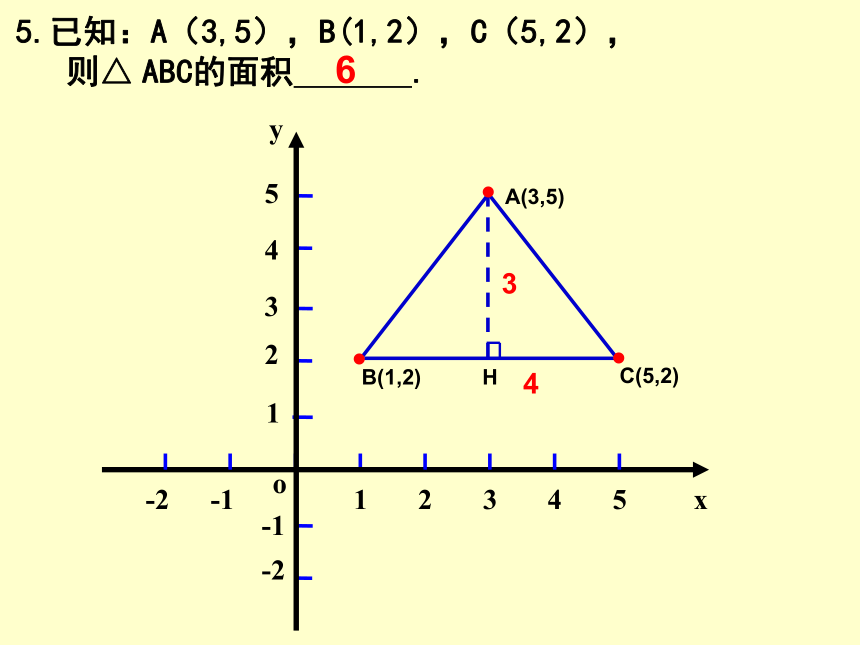
5.已知:A(3,5),B(1,2),C(5,2),
则△
ABC的面积
.
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
6
?
?
?
B(1,2)
A(3,5)
C(5,2)
H
4
3
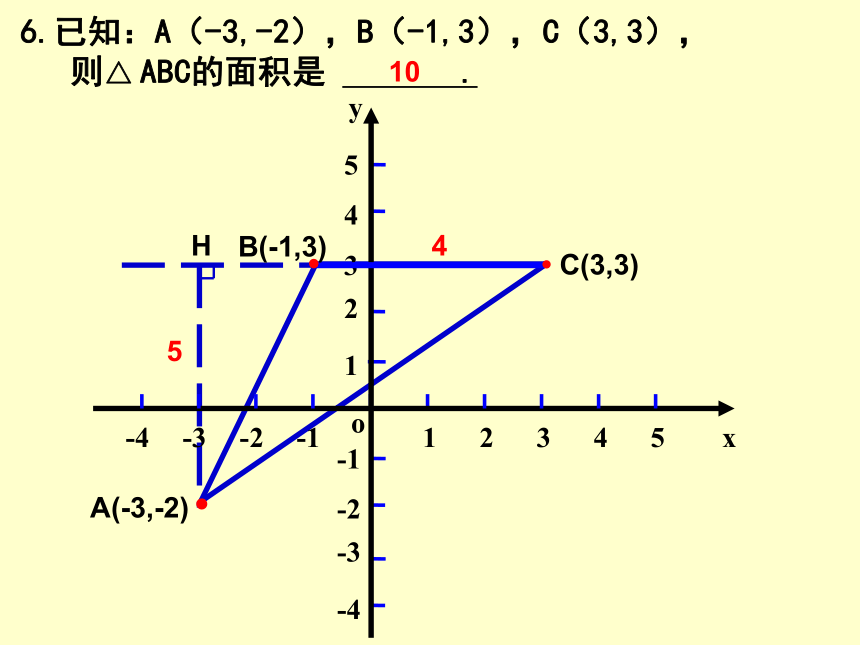
6.已知:A(-3,-2),B(-1,3),C(3,3),
则△
ABC的面积是
.
o
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
x
y
A(-3,-2)
?
?
?
C(3,3)
B(-1,3)
10
H
4
5
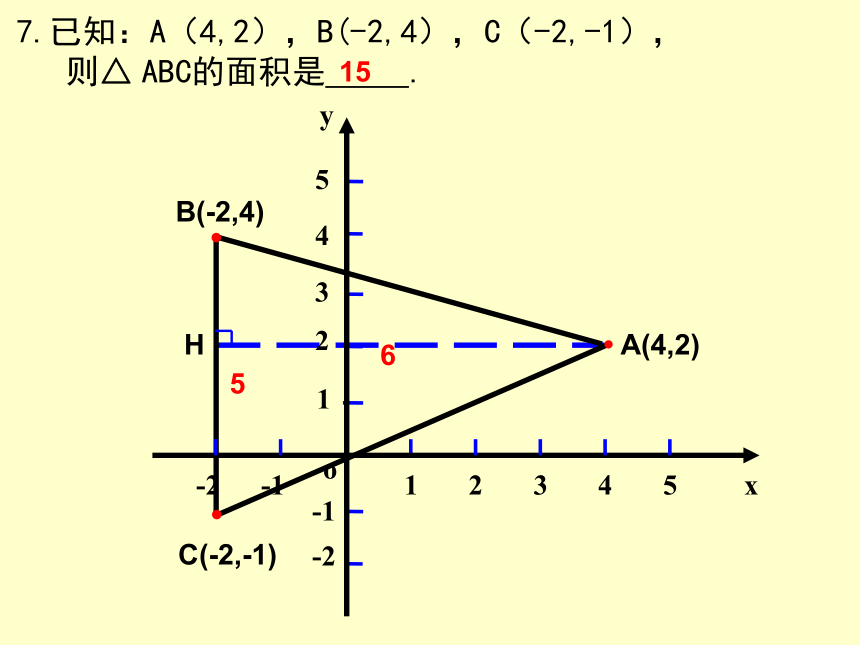
7.已知:A(4,2),B(-2,4),C(-2,-1),
则△
ABC的面积是
.
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
A(4,2)
?
?
C(-2,-1)
15
H
B(-2,4)
5
6
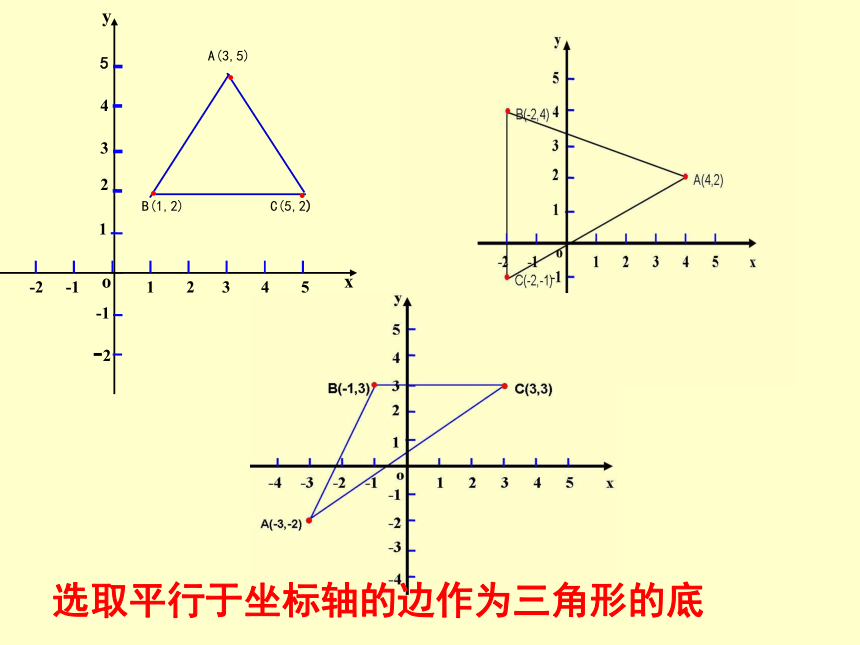
选取平行于坐标轴的边作为三角形的底
-2
y
o
1
-2
-1
3
4
2
5
1
2
3
4
5
-1
x
?
?
B(1,2)
A(3,5)
C(5,2)
?
在平面直角坐标系中,如果三角形有一条边在坐标轴上(或平行于坐标轴),可根据这条边的两个顶点的坐标求出这条边的长,再利用这条边所对的顶点的坐标求出该边上的高,从而求出三角形的面积.
归纳总结
8.如图所示,四边形ABCD的面积是
.
?
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
D(0,-1)
A(-2,0)
B(0,2)
C(3,0)
?
?
?
7.5
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
9.如图所示,△
OAB的面积是
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
利用现在所学过的知识你能确定M点的坐标吗?
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
利用现在所学过的知识你能确定M点的坐标吗?
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
N
M
S=S梯形OAMN–
S1
–S2
s1
s2
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
S=S梯形OPMB–
S1
–S2
P
s1
s2
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
N
M
S=S长方形OPMN–
S1
–
S2
–S3
P
s1
s2
s3
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
S=S
△
BOM+
S梯形BMPA–
S
△
AOP
P
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
9.如图所示,求△
OAB的面积。
S
△AOB=7
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
10.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
H
s1
s2
S=S1+S2
10.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
s1
s2
S=S1+S2
9.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
N
s1
S=S梯形NOBC
–
S1
9.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
N
M
s1
s2
S=S长方形NOBM–
S1
–S2
9.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
10.如图所示,则四边形AOBC的面积是
。
S
四边形AOBC=13
在平面直角坐标系中,若三角形无边在坐标轴上或平行于坐标轴,或不规则的多边形的面积不能直接求出时,可以利用“分割”或“补形”,将图形通过添辅助线转化为有边与坐标轴平行或在坐标轴上的图形进行计算.
归纳总结
1.等积变换
2.割补法求面积
谈谈我们的收获
化未知为已知
化复杂为简单
数学思想
数学方法
已知点O(0,0),B(1,2),点A在坐标轴上,且三角形OAB的面积为2,求满足条件的点A的坐标.
课后探究
A(2,0)
A(-2,0)
A(0,4)
A(0,-4)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
B(1,2)
-3
-4
平面直角坐标系中图形面积的求法
在平面直角坐标系中描出下列各点,并求出线段的长度.
(1)若A(-1,0),B(5,0),则线段AB的长为____
(2)若C(0,3),D(0,-2),则线段CD的长为_____
(3)若E(-1,3),F(3,3),则线段EF的长为_____
(4)若M(-2,4),N(-2,-1),则线段MN的长为___
6
4
5
5
你发现了什么规律?
预备知识
预备知识
P(ɑ,b)
在平面直角坐标系中,
点P(ɑ,b)到x轴的距离等于
到y轴的距离等于
M(d,b)
Q(ɑ,c)
(2)若P(ɑ,
b),Q(ɑ,c),M(d,b),则
PM∥
轴,PQ
∥
轴,
MP长为
,PQ长为
x
y
x
y
O
二、探究规律
1.如图所示,△AOB的面积是
.
6
B(3,0)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
?
? A(0,4)
2.如图所示,
△
ABC的面积是
.
C(3,0)
B(-2,0)
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
?
?
A(0,5)
12.5
3.如图所示,
△
ABC的面积是
.
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
H
7.5
?
C(0,-2)
A(-3,-1)
?
?
B(0,3)
3
5
B(5,0)
4.
如图所示,
△
ABC的面积是
.
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
?
C(3,
-
4)
H
A(-1,0)
?
?
12
6
4
选取在坐标轴上的边作为三角形的底
5.已知:A(3,5),B(1,2),C(5,2),
则△
ABC的面积
.
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
6
?
?
?
B(1,2)
A(3,5)
C(5,2)
H
4
3
6.已知:A(-3,-2),B(-1,3),C(3,3),
则△
ABC的面积是
.
o
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
x
y
A(-3,-2)
?
?
?
C(3,3)
B(-1,3)
10
H
4
5
7.已知:A(4,2),B(-2,4),C(-2,-1),
则△
ABC的面积是
.
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
A(4,2)
?
?
C(-2,-1)
15
H
B(-2,4)
5
6
选取平行于坐标轴的边作为三角形的底
-2
y
o
1
-2
-1
3
4
2
5
1
2
3
4
5
-1
x
?
?
B(1,2)
A(3,5)
C(5,2)
?
在平面直角坐标系中,如果三角形有一条边在坐标轴上(或平行于坐标轴),可根据这条边的两个顶点的坐标求出这条边的长,再利用这条边所对的顶点的坐标求出该边上的高,从而求出三角形的面积.
归纳总结
8.如图所示,四边形ABCD的面积是
.
?
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
D(0,-1)
A(-2,0)
B(0,2)
C(3,0)
?
?
?
7.5
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
9.如图所示,△
OAB的面积是
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
利用现在所学过的知识你能确定M点的坐标吗?
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
利用现在所学过的知识你能确定M点的坐标吗?
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
N
M
S=S梯形OAMN–
S1
–S2
s1
s2
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
S=S梯形OPMB–
S1
–S2
P
s1
s2
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
N
M
S=S长方形OPMN–
S1
–
S2
–S3
P
s1
s2
s3
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
M
S=S
△
BOM+
S梯形BMPA–
S
△
AOP
P
9.如图所示,求△
OAB的面积.
?
A(5,2)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
B(3,4)
?
9.如图所示,求△
OAB的面积。
S
△AOB=7
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
10.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
H
s1
s2
S=S1+S2
10.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
s1
s2
S=S1+S2
9.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
N
s1
S=S梯形NOBC
–
S1
9.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
N
M
s1
s2
S=S长方形NOBM–
S1
–S2
9.如图所示,则四边形AOBC的面积是
。
?
B(5,0)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
?
?
A(0,2)
C(3,4)
?
10.如图所示,则四边形AOBC的面积是
。
S
四边形AOBC=13
在平面直角坐标系中,若三角形无边在坐标轴上或平行于坐标轴,或不规则的多边形的面积不能直接求出时,可以利用“分割”或“补形”,将图形通过添辅助线转化为有边与坐标轴平行或在坐标轴上的图形进行计算.
归纳总结
1.等积变换
2.割补法求面积
谈谈我们的收获
化未知为已知
化复杂为简单
数学思想
数学方法
已知点O(0,0),B(1,2),点A在坐标轴上,且三角形OAB的面积为2,求满足条件的点A的坐标.
课后探究
A(2,0)
A(-2,0)
A(0,4)
A(0,-4)
1
-2
-1
3
4
2
5
1
2
3
4
5
-2
-1
x
y
o
B(1,2)
-3
-4
