2020-2021学年北师大版七年级数学下册第3章变量之间的关系经典好题优生辅导训练(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第3章变量之间的关系经典好题优生辅导训练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 00:00:00 | ||
图片预览



文档简介
2021年北师大版七年级数学下册第3章变量之间的关系经典好题优生辅导训练(附答案)
1.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
2.一辆客车从酒泉出发开往兰州,设客车出发t小时后与兰州的距离为s千米,下列图象能大致反映s与t之间的函数关系的是( )
A.
B.
C.
D.
3.如图1,在矩形MNPO中,动点R从点N出发,沿N→P→O→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPO的周长是( )
A.11
B.15
C.16
D.24
4.为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费a元;若超过10吨,则10吨水按每吨a元收费,超过10吨的部分按每吨b元收费,公司为居民绘制的水费y(元)与当月用水量x(吨)之间的函数图象如下,则下列结论错误的是( )
A.a=1.5
B.b=2
C.若小明家3月份用水14吨,则应缴水费23元
D.若小明家7月份缴水费30元,则该用户当月用水18.5吨
5.在某一阶段,某商品的销售量与销售价之间存在如表关系:
销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元,销售量为y件,估计:当x=127时,y的值为( )
A.63
B.59
C.53
D.43
6.某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是( )
A.每月上网不足25小时,选择A方式最省钱
B.每月上网时间为30小时,选择B方式最省钱
C.每月上网费用为60元,选择B方式比A方式时间长
D.每月上网时间超过70小时,选择C方式最省钱
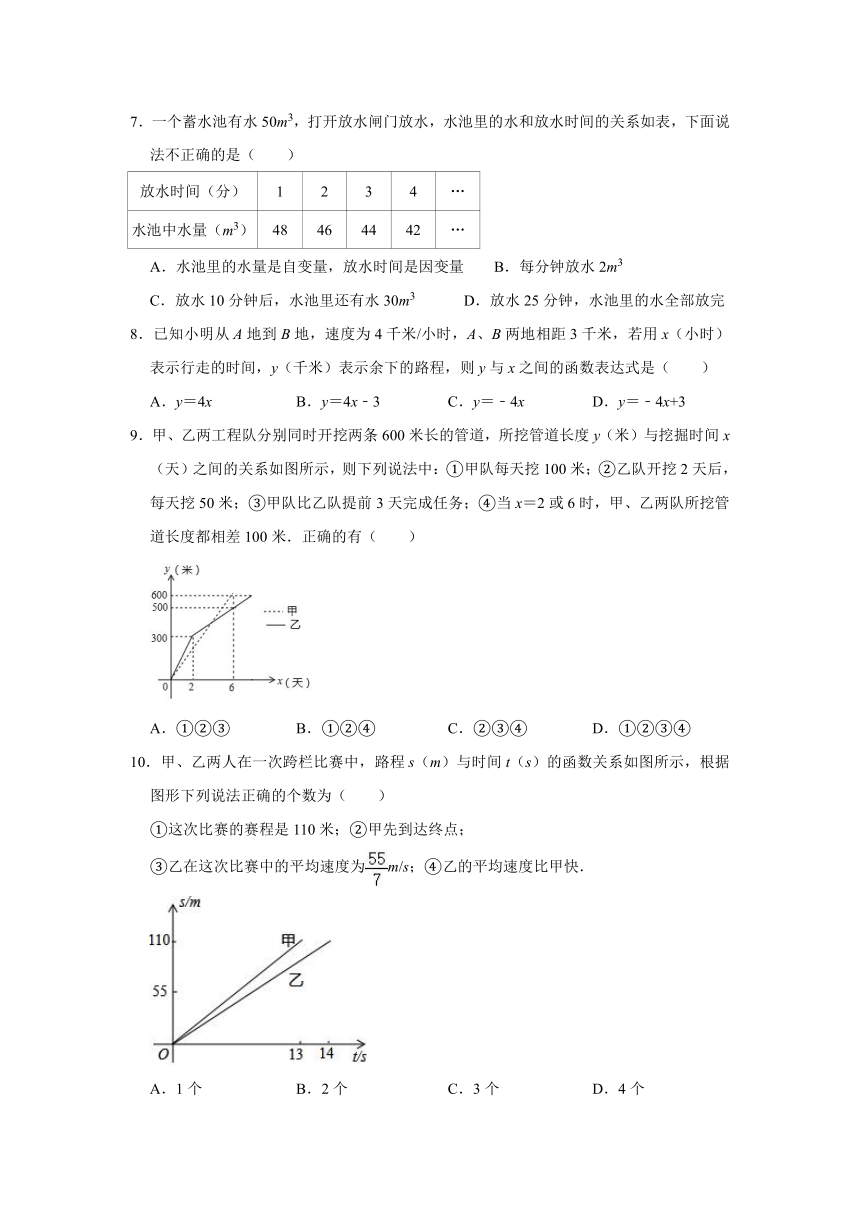
7.一个蓄水池有水50m3,打开放水闸门放水,水池里的水和放水时间的关系如表,下面说法不正确的是( )
放水时间(分)
1
2
3
4
…
水池中水量(m3)
48
46
44
42
…
A.水池里的水量是自变量,放水时间是因变量
B.每分钟放水2m3
C.放水10分钟后,水池里还有水30m3
D.放水25分钟,水池里的水全部放完
8.已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )
A.y=4x
B.y=4x﹣3
C.y=﹣4x
D.y=﹣4x+3
9.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖2天后,每天挖50米;③甲队比乙队提前3天完成任务;④当x=2或6时,甲、乙两队所挖管道长度都相差100米.正确的有( )
A.①②③
B.①②④
C.②③④
D.①②③④
10.甲、乙两人在一次跨栏比赛中,路程s(m)与时间t(s)的函数关系如图所示,根据图形下列说法正确的个数为( )
①这次比赛的赛程是110米;②甲先到达终点;
③乙在这次比赛中的平均速度为m/s;④乙的平均速度比甲快.
A.1个
B.2个
C.3个
D.4个
11.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离s(单位:米)与时间t(单位:分钟)的对应关系如图所示,则文具店与小张家的距离为
.
12.如果乘坐出租车所付款金额y(元)与乘坐距离x(千米)之间的函数图象由线段AB、线段BC和射线CD组成(如图所示),那么乘坐该出租车8(千米)需要支付的金额为
元.
13.如图,某学校组织团员举行防溺水宣传活动,从学校骑车出发,先上坡到达A地后,宣传8min;然后下坡到B地宣传8min返回,行程情况如图.若返回时,上、下坡的速度仍保持不变,那么他们直接从B地返回学校用的时间是
min.
14.学校举办庆元旦智力竞赛,竞赛的记分方法是:开始前,每位参赛者都有100分作为底分,竞赛中每答对一个问题加10分,答错或不答得0分.代表某班参赛的小亮答对问题为x个,小亮的竞赛总得分为y(分),那么y与x之间的关系式为
.
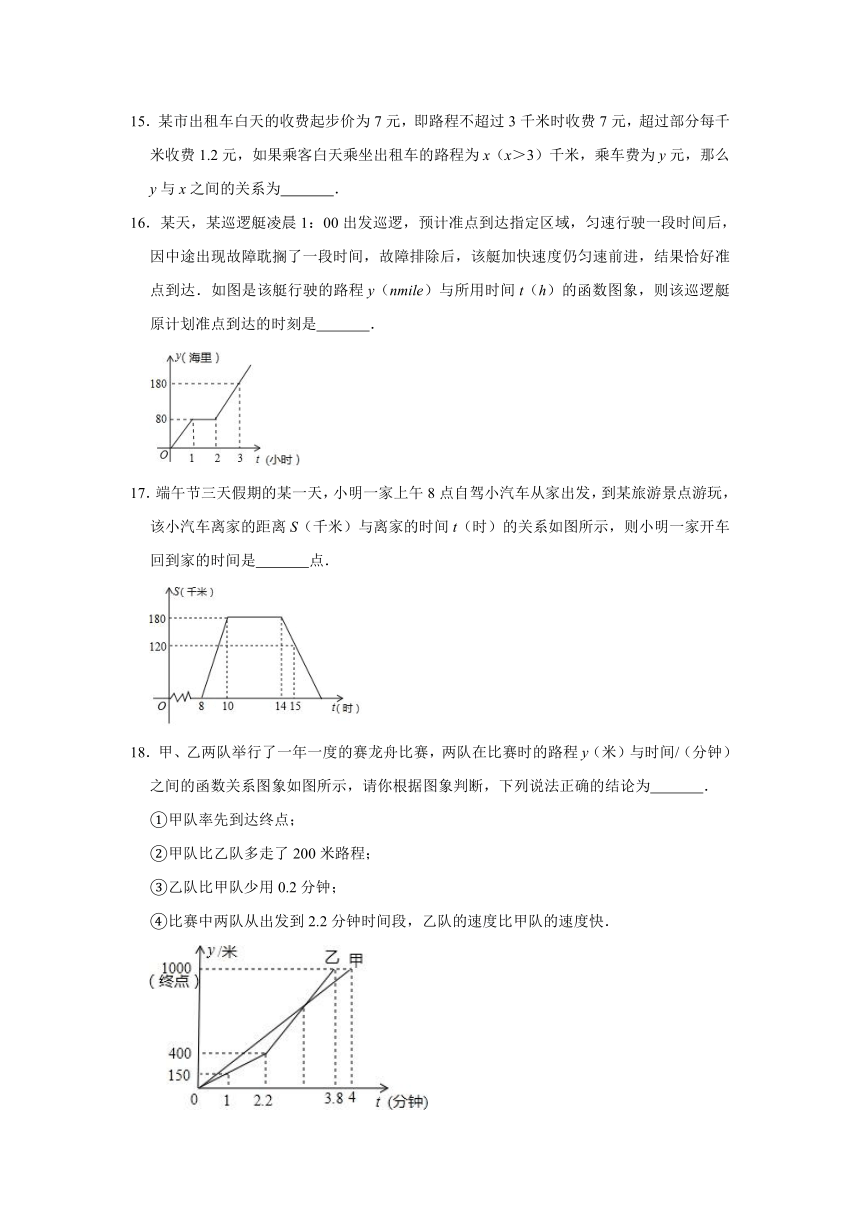
15.某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为
.
16.某天,某巡逻艇凌晨1:00出发巡逻,预计准点到达指定区域,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(nmile)与所用时间t(h)的函数图象,则该巡逻艇原计划准点到达的时刻是
.
17.端午节三天假期的某一天,小明一家上午8点自驾小汽车从家出发,到某旅游景点游玩,该小汽车离家的距离S(千米)与离家的时间t(时)的关系如图所示,则小明一家开车回到家的时间是
点.
18.甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程y(米)与时间/(分钟)之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的结论为
.
①甲队率先到达终点;
②甲队比乙队多走了200米路程;
③乙队比甲队少用0.2分钟;
④比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快.
19.甲骑自行车、乙骑摩托车沿相同路线匀速由A地到B地,行驶过程中路程与时间的函数关系如图所示.根据图象信息可知,乙在甲骑行
分钟时追上甲.
20.如图所示,甲、乙两车在某时间段内速度随时间变化的图象.下列结论:
①甲的速度始终保持不变;
②乙车第12秒时的速度为32米/秒;
③乙车前4秒行驶的总路程为48米.
其中正确的是
.(填序号)
21.某种车的油箱加满油后,油箱中的剩余油量y(升)与车行驶路程x(千米)之间的关系,如图所示,根据图象回答下列问题:
(1)这种车的油箱最多能装
升油.
(2)加满油后可供该车行驶
千米.
(3)该车每行驶200千米消耗汽油
升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶
千米后,车辆将自动报警?
22.某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
(1)学校离他家
米,从出发到学校,王老师共用了
分钟;王老师吃早餐用了
分钟?
(2)观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?
23.由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.蓄水量y(万立方米)与干旱时间t(天)之间的关系如图所示,回答下列问题:
(1)干旱持续到第10天,水库的蓄水量为
万立方米.
(2)若水库的蓄水量小于360万立方米时,将发生严重干旱警报,那么多少天后将发生严重干旱警报?
(3)在(2)的条件下,照这样干旱下去,预计再持续多少天时,水库将干涸.
24.琳琳通过新闻了解到,近来意大利“新冠肺炎”疫情愈发严重,决定给意大利的网友Carlo邮寄一批防疫用品.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后再走回家.琳琳离家的距离y与时间x之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为
km.
(2)琳琳邮寄物品用了
min.
(3)琳琳两段步行的速度分别是多少?
(4)图中点P的意义是
.
25.新冠病毒防疫期间,草莓摊主小钱为避免交叉感染的风险,建议顾客选择微信支付,尽量不使用现金,早上开始营业前,他查看了自己的微信零钱;销售完20kg后,他又一次查看了微信零钱,由于草莓所剩不多,他想早点卖完回家,于是每千克降价10元销售,很快销售一空,小钱弟弟根据小钱的微信零钱(元)与销售草莓数量(kg)之间的关系绘制了下列图象,请你根据以上信息回答下列问题:
(1)图象中A点表示的意义是什么?
(2)降价前草莓每千克售价多少元?
(3)小钱卖完所有草莓微信零钱应有多少元?
26.甲、乙两人沿相同的路线骑行由A地到B地,骑行过程中路程与时间关系的图象如图所示.根据图象解答下列问题:
(1)甲、乙两人谁先到达终点?先到多长时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中?(不包括起点和终点)
(4)当甲、乙两人途中相遇时,直接写出相遇地与A地的距离.
27.某地举行龙舟赛,甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:
(1)最先到达终点的是
队,比另一队领先
分钟到达;
(2)在比赛过程中,甲队的速度始终保持为
米/分;而乙队在第
分钟后第一次加速,速度变为
米/分,在第
分钟后第二次加速;
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
参考答案
1.解:由图象可知,小华和小明的家离学校1200米,故A正确;
根据图象,小华乘公共汽车,从出发到到达学校共用了13﹣8=5(分钟),所以公共汽车的速度为1200÷5=240(米/分),故B正确;
小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是8+480÷240=10(分钟),即7:50相遇,故C正确;
小明从家到学校的时间为20分钟,所以小明的平均速度为1200÷20=60(米/分),故D错误.
故选:D.
2.解:根据出发时与终点这两个特殊点的意义,象能大致反映s与t之间的函数关系的是应选A.
故选:A.
3.解:∵x=3时,及R从N到达点P时,面积开始不变,
∴PN=3,
同理可得OP=5,
∴矩形的周长为2(3+5)=16.
故选:C.
4.解:由图象可知,a=15÷10=1.5;
b==2;
用水14吨,则应缴水费:1.5×10+2×(14﹣10)=15+8=23(元);
缴水费30元,则该用户当月用水为:10+(30﹣15)÷2=17.5(吨).
故结论错误的是选项D.
故选:D.
5.解:由图表可以看出y与x符合一次函数关系,设y=kx+b(k≠0),
把x=90,y=90和x=100,y=80代入得,
,
解得:,
则y=﹣x+180,
当x=127时,y=﹣127+180=53.
故选:C.
6.解:由题意可知:
A、每月上网不足25小时,选择A方式最省钱,故本选项不合题意;
B、每月上网时间为30小时,选择A方式的费用为:30+5×[(120﹣30)÷(50﹣25)]=48(元),B方式为50元,C方式为120元,所以选择A方式最省钱,故本选项符合题意;
C、每月上网费用为60元,选择B方式比A方式时间长,故本选项不合题意;
D、每月上网时间超过70小时,选择C方式最省钱,故本选项不合题意;
故选:B.
7.解:设蓄水量为y,时间为t,
则可得y=50﹣2t,
A、放水时间是自变量,水池里的水量是因变量,故本选项符合题意;
B、蓄水池每分钟放水2m3,故本选项不合题意;
C、放水10分钟后,水池中水量为:y=50﹣2×10=30m3,故本选项不合题意;
D、蓄水池一共可以放水25分钟,故本选项不合题意;
故选:A.
8.解:用x(小时)表示行走的时间,y(千米)表示余下的路程,
则y与x之间的函数表达式是:y=3﹣4x=﹣4x+3.
故选:D.
9.解:①根据函数图象得:
甲队的工作效率为:600÷6=100(米/天),故正确;
②根据函数图象,
得乙队开挖两天后的工作效率为:(500﹣300)÷(6﹣2)=50(米/天),故正确;
③乙队完成任务的时间为:2+(600﹣300)÷50=8(天),
∴甲队提前的时间为:8﹣6=2(天).
∵2≠3,
∴③错误;
④当x=2时,甲队完成的工作量为:2×100=200(米),
乙队完成的工作量为:300米.
当x=6时,甲队完成的工作量为600米,乙队完成的工作量为500米.
∵300﹣200=600﹣500=100(米),
∴当x=2或6时,甲乙两队所挖管道长度都相差100米.故正确.
正确的有:①②④.
故选:B.
10.解:由图象可知,
这次比赛的赛程是110米,故①说法正确;
甲先到达终点,故②说法正确;
乙在这次比赛中的平均速度为:(m/s),故③说法正确;
甲的平均速度比乙快,故④说法错误.
所以正确的个数为3个.
故选:C.
11.解:小张骑车的速度=1500÷(6﹣1)=300米/分钟.
文具店与小张家的距离=1500﹣300×2=900米.
故答案为:900米.
12.解:乘坐该出租车8(千米)需要支付的金额为:14+(30.8﹣14)÷(10﹣3)×(8﹣3)=26(元).
故答案为:26.
13.解:如图,
由题意可得,OA段为上坡,上坡的速度为:,
CB段为下坡,下坡的速度为:,
返回时,先上坡,再下坡;
上坡时间:,
上坡时间:min,
返回时所用时间为:30+7.2=37.2min.
故答案为:37.2.
14.解:根据题意得:
y=10x+100.
故答案为:y=10x+100.
15.解:依据题意得:y=7+1.2(x﹣3)=1.2x+3.4,
故答案为:y=1.2x+3.4,
16.解:设原计划行驶的时间为t小时,
根据题意得,80t=80+100(t﹣2),
解得:t=6,
故计划准点到达的时刻为:7:00.
故答案为:7:00.
17.解:由图象可得,景点离小明家180千米;
小明从景点回家的行驶速度为:(千米/时),
所以小明一家开车回到家的时间是:14+180÷60=17(时).
故答案为:17.
18.解:①从图象看,乙先到达终点,故原说法错误;
②从图象看,甲乙走的距离都是1000米,故原说法错误;
③从图象看,乙队比甲队少用0.2分钟,故原说法正确;
④从图象看,比赛中两队从出发到2.2分钟时间段,甲队的速度比乙队的速度快,故原说法错误;
故答案为:③.
19.解:由题意得:
甲的速度为:(km/min),
乙的速度为:(km/min),
设乙在甲骑行x分钟时追上甲,根据题意得:
0.2x=0.4(x﹣10),
解得x=20.
所以乙在甲骑行20分钟时追上甲.
故答案为:20.
20.解:由图象可知,
甲的速度逐渐增大,故①说法错误;
乙车第12秒时的速度为32米/秒,故②说法正确;
乙车前4秒行驶的总路程为:12×4=48(米),故③说法正确.
故答案为:②③.
21.解:(1)这种车的油箱最多能装50升油.
(2)加满油后可供该车行驶1000千米.
(3)该车每行驶200千米消耗汽油10升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶800千米后,车辆将自动报警.
故答案为:(1)50;(2)1000;(3)10;(4)800.
22.解:(1)由图象可知,学校离他家1000米,从出发到学校,王老师共用了25分钟;王老师吃早餐用了20﹣10=10(分钟),
故答案为:1000,25,10;
(2)根据图象可得:王老师吃早餐以前的速度为:(米/分),吃完早餐以后的速度为:(米/分),
50<100,
答:吃完早餐以后的速度快.
23.解:(1)由图象可知,干旱持续到第10天,水库的蓄水量为1200万立方米.
故答案为:1200;
(2)(1500﹣1200)÷10=30(万立方米),
(1500﹣360)÷30=38(天),
答:38天后将发生严重干旱警报;
(3)1500÷30﹣38=12(天),
答:照这样干旱下去,预计再持续12天时,水库将干涸.
24.解:(1)由图象可知,琳琳家离药店的距离为2.5km.
故答案为:2.5;
(2)由图象可知,琳琳邮寄物品用了:65﹣45=20(分钟),
故答案为:20;
(3)从药店步行到邮局的路程为1km,时间为15min,所以速度为km/min;
从邮局步行回家的路程为1.5km,时间为25min,所以速度为:(km/min);
(4)图中点P的意义是:离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.
故答案为:离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.
25.解:(1)由图象可知,小钱开始营业前微信零钱有50元;
(2)由图象可知,销售草莓20kg后,小钱的微信零钱为650元,
∴销售草莓20kg,销售收入为650﹣50=600元,
∴降价前草莓每千克售价为:600÷20=30(元);
(3)降价后草莓每千克售价为:30﹣10=20元,
∴小钱卖完所有草莓微信零钱为:650+5×20=750(元),
答:小钱卖完所有草莓微信零钱应该有750元.
26.解:由图象可知:
(1)甲先到达终点,先到5分钟;
(2)甲的行驶速度为:6÷(25﹣5)=0.3(千米/分);
乙的行驶速度为:6÷30=0.2(千米/分);
(3)在乙出发后5分钟到25分钟,两人均行驶在途中;
(4)当甲、乙两人途中相遇时,相遇地与A地的距离为3千米.
27.解:(1)由函数图象得:
最先到达终点的是乙队,比另一队领先6﹣5=1分钟到达.
故答案为:乙,1;
(2)由函数图象得:
甲的速度为:900÷6=150米/分,而乙队在第2分钟后第一次加速,其速度为(500﹣200)÷2=150米/分,第4分钟后第二次加速.
故答案为:150,2,150,4;
(3)乙队在第一次加速后,始终保持这个速度继续前进走完余下路程需要的时间为
700÷150=,
∴乙队走完全程的时间为分钟.
∵甲队行驶完全程需要的时间是6分钟.,
∴甲先到达终点
1.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
2.一辆客车从酒泉出发开往兰州,设客车出发t小时后与兰州的距离为s千米,下列图象能大致反映s与t之间的函数关系的是( )
A.
B.
C.
D.
3.如图1,在矩形MNPO中,动点R从点N出发,沿N→P→O→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPO的周长是( )
A.11
B.15
C.16
D.24
4.为增强居民节水意识,我市自来水公司采用以户为单位分段计费办法收费,即每月用水不超过10吨,每吨收费a元;若超过10吨,则10吨水按每吨a元收费,超过10吨的部分按每吨b元收费,公司为居民绘制的水费y(元)与当月用水量x(吨)之间的函数图象如下,则下列结论错误的是( )
A.a=1.5
B.b=2
C.若小明家3月份用水14吨,则应缴水费23元
D.若小明家7月份缴水费30元,则该用户当月用水18.5吨
5.在某一阶段,某商品的销售量与销售价之间存在如表关系:
销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元,销售量为y件,估计:当x=127时,y的值为( )
A.63
B.59
C.53
D.43
6.某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是( )
A.每月上网不足25小时,选择A方式最省钱
B.每月上网时间为30小时,选择B方式最省钱
C.每月上网费用为60元,选择B方式比A方式时间长
D.每月上网时间超过70小时,选择C方式最省钱
7.一个蓄水池有水50m3,打开放水闸门放水,水池里的水和放水时间的关系如表,下面说法不正确的是( )
放水时间(分)
1
2
3
4
…
水池中水量(m3)
48
46
44
42
…
A.水池里的水量是自变量,放水时间是因变量
B.每分钟放水2m3
C.放水10分钟后,水池里还有水30m3
D.放水25分钟,水池里的水全部放完
8.已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )
A.y=4x
B.y=4x﹣3
C.y=﹣4x
D.y=﹣4x+3
9.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖2天后,每天挖50米;③甲队比乙队提前3天完成任务;④当x=2或6时,甲、乙两队所挖管道长度都相差100米.正确的有( )
A.①②③
B.①②④
C.②③④
D.①②③④
10.甲、乙两人在一次跨栏比赛中,路程s(m)与时间t(s)的函数关系如图所示,根据图形下列说法正确的个数为( )
①这次比赛的赛程是110米;②甲先到达终点;
③乙在这次比赛中的平均速度为m/s;④乙的平均速度比甲快.
A.1个
B.2个
C.3个
D.4个
11.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离s(单位:米)与时间t(单位:分钟)的对应关系如图所示,则文具店与小张家的距离为
.
12.如果乘坐出租车所付款金额y(元)与乘坐距离x(千米)之间的函数图象由线段AB、线段BC和射线CD组成(如图所示),那么乘坐该出租车8(千米)需要支付的金额为
元.
13.如图,某学校组织团员举行防溺水宣传活动,从学校骑车出发,先上坡到达A地后,宣传8min;然后下坡到B地宣传8min返回,行程情况如图.若返回时,上、下坡的速度仍保持不变,那么他们直接从B地返回学校用的时间是
min.
14.学校举办庆元旦智力竞赛,竞赛的记分方法是:开始前,每位参赛者都有100分作为底分,竞赛中每答对一个问题加10分,答错或不答得0分.代表某班参赛的小亮答对问题为x个,小亮的竞赛总得分为y(分),那么y与x之间的关系式为
.
15.某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为
.
16.某天,某巡逻艇凌晨1:00出发巡逻,预计准点到达指定区域,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(nmile)与所用时间t(h)的函数图象,则该巡逻艇原计划准点到达的时刻是
.
17.端午节三天假期的某一天,小明一家上午8点自驾小汽车从家出发,到某旅游景点游玩,该小汽车离家的距离S(千米)与离家的时间t(时)的关系如图所示,则小明一家开车回到家的时间是
点.
18.甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程y(米)与时间/(分钟)之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的结论为
.
①甲队率先到达终点;
②甲队比乙队多走了200米路程;
③乙队比甲队少用0.2分钟;
④比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快.
19.甲骑自行车、乙骑摩托车沿相同路线匀速由A地到B地,行驶过程中路程与时间的函数关系如图所示.根据图象信息可知,乙在甲骑行
分钟时追上甲.
20.如图所示,甲、乙两车在某时间段内速度随时间变化的图象.下列结论:
①甲的速度始终保持不变;
②乙车第12秒时的速度为32米/秒;
③乙车前4秒行驶的总路程为48米.
其中正确的是
.(填序号)
21.某种车的油箱加满油后,油箱中的剩余油量y(升)与车行驶路程x(千米)之间的关系,如图所示,根据图象回答下列问题:
(1)这种车的油箱最多能装
升油.
(2)加满油后可供该车行驶
千米.
(3)该车每行驶200千米消耗汽油
升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶
千米后,车辆将自动报警?
22.某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
(1)学校离他家
米,从出发到学校,王老师共用了
分钟;王老师吃早餐用了
分钟?
(2)观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?
23.由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.蓄水量y(万立方米)与干旱时间t(天)之间的关系如图所示,回答下列问题:
(1)干旱持续到第10天,水库的蓄水量为
万立方米.
(2)若水库的蓄水量小于360万立方米时,将发生严重干旱警报,那么多少天后将发生严重干旱警报?
(3)在(2)的条件下,照这样干旱下去,预计再持续多少天时,水库将干涸.
24.琳琳通过新闻了解到,近来意大利“新冠肺炎”疫情愈发严重,决定给意大利的网友Carlo邮寄一批防疫用品.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后再走回家.琳琳离家的距离y与时间x之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为
km.
(2)琳琳邮寄物品用了
min.
(3)琳琳两段步行的速度分别是多少?
(4)图中点P的意义是
.
25.新冠病毒防疫期间,草莓摊主小钱为避免交叉感染的风险,建议顾客选择微信支付,尽量不使用现金,早上开始营业前,他查看了自己的微信零钱;销售完20kg后,他又一次查看了微信零钱,由于草莓所剩不多,他想早点卖完回家,于是每千克降价10元销售,很快销售一空,小钱弟弟根据小钱的微信零钱(元)与销售草莓数量(kg)之间的关系绘制了下列图象,请你根据以上信息回答下列问题:
(1)图象中A点表示的意义是什么?
(2)降价前草莓每千克售价多少元?
(3)小钱卖完所有草莓微信零钱应有多少元?
26.甲、乙两人沿相同的路线骑行由A地到B地,骑行过程中路程与时间关系的图象如图所示.根据图象解答下列问题:
(1)甲、乙两人谁先到达终点?先到多长时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中?(不包括起点和终点)
(4)当甲、乙两人途中相遇时,直接写出相遇地与A地的距离.
27.某地举行龙舟赛,甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图象如图所示,根据函数图象填空和解答问题:
(1)最先到达终点的是
队,比另一队领先
分钟到达;
(2)在比赛过程中,甲队的速度始终保持为
米/分;而乙队在第
分钟后第一次加速,速度变为
米/分,在第
分钟后第二次加速;
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
参考答案
1.解:由图象可知,小华和小明的家离学校1200米,故A正确;
根据图象,小华乘公共汽车,从出发到到达学校共用了13﹣8=5(分钟),所以公共汽车的速度为1200÷5=240(米/分),故B正确;
小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是8+480÷240=10(分钟),即7:50相遇,故C正确;
小明从家到学校的时间为20分钟,所以小明的平均速度为1200÷20=60(米/分),故D错误.
故选:D.
2.解:根据出发时与终点这两个特殊点的意义,象能大致反映s与t之间的函数关系的是应选A.
故选:A.
3.解:∵x=3时,及R从N到达点P时,面积开始不变,
∴PN=3,
同理可得OP=5,
∴矩形的周长为2(3+5)=16.
故选:C.
4.解:由图象可知,a=15÷10=1.5;
b==2;
用水14吨,则应缴水费:1.5×10+2×(14﹣10)=15+8=23(元);
缴水费30元,则该用户当月用水为:10+(30﹣15)÷2=17.5(吨).
故结论错误的是选项D.
故选:D.
5.解:由图表可以看出y与x符合一次函数关系,设y=kx+b(k≠0),
把x=90,y=90和x=100,y=80代入得,
,
解得:,
则y=﹣x+180,
当x=127时,y=﹣127+180=53.
故选:C.
6.解:由题意可知:
A、每月上网不足25小时,选择A方式最省钱,故本选项不合题意;
B、每月上网时间为30小时,选择A方式的费用为:30+5×[(120﹣30)÷(50﹣25)]=48(元),B方式为50元,C方式为120元,所以选择A方式最省钱,故本选项符合题意;
C、每月上网费用为60元,选择B方式比A方式时间长,故本选项不合题意;
D、每月上网时间超过70小时,选择C方式最省钱,故本选项不合题意;
故选:B.
7.解:设蓄水量为y,时间为t,
则可得y=50﹣2t,
A、放水时间是自变量,水池里的水量是因变量,故本选项符合题意;
B、蓄水池每分钟放水2m3,故本选项不合题意;
C、放水10分钟后,水池中水量为:y=50﹣2×10=30m3,故本选项不合题意;
D、蓄水池一共可以放水25分钟,故本选项不合题意;
故选:A.
8.解:用x(小时)表示行走的时间,y(千米)表示余下的路程,
则y与x之间的函数表达式是:y=3﹣4x=﹣4x+3.
故选:D.
9.解:①根据函数图象得:
甲队的工作效率为:600÷6=100(米/天),故正确;
②根据函数图象,
得乙队开挖两天后的工作效率为:(500﹣300)÷(6﹣2)=50(米/天),故正确;
③乙队完成任务的时间为:2+(600﹣300)÷50=8(天),
∴甲队提前的时间为:8﹣6=2(天).
∵2≠3,
∴③错误;
④当x=2时,甲队完成的工作量为:2×100=200(米),
乙队完成的工作量为:300米.
当x=6时,甲队完成的工作量为600米,乙队完成的工作量为500米.
∵300﹣200=600﹣500=100(米),
∴当x=2或6时,甲乙两队所挖管道长度都相差100米.故正确.
正确的有:①②④.
故选:B.
10.解:由图象可知,
这次比赛的赛程是110米,故①说法正确;
甲先到达终点,故②说法正确;
乙在这次比赛中的平均速度为:(m/s),故③说法正确;
甲的平均速度比乙快,故④说法错误.
所以正确的个数为3个.
故选:C.
11.解:小张骑车的速度=1500÷(6﹣1)=300米/分钟.
文具店与小张家的距离=1500﹣300×2=900米.
故答案为:900米.
12.解:乘坐该出租车8(千米)需要支付的金额为:14+(30.8﹣14)÷(10﹣3)×(8﹣3)=26(元).
故答案为:26.
13.解:如图,
由题意可得,OA段为上坡,上坡的速度为:,
CB段为下坡,下坡的速度为:,
返回时,先上坡,再下坡;
上坡时间:,
上坡时间:min,
返回时所用时间为:30+7.2=37.2min.
故答案为:37.2.
14.解:根据题意得:
y=10x+100.
故答案为:y=10x+100.
15.解:依据题意得:y=7+1.2(x﹣3)=1.2x+3.4,
故答案为:y=1.2x+3.4,
16.解:设原计划行驶的时间为t小时,
根据题意得,80t=80+100(t﹣2),
解得:t=6,
故计划准点到达的时刻为:7:00.
故答案为:7:00.
17.解:由图象可得,景点离小明家180千米;
小明从景点回家的行驶速度为:(千米/时),
所以小明一家开车回到家的时间是:14+180÷60=17(时).
故答案为:17.
18.解:①从图象看,乙先到达终点,故原说法错误;
②从图象看,甲乙走的距离都是1000米,故原说法错误;
③从图象看,乙队比甲队少用0.2分钟,故原说法正确;
④从图象看,比赛中两队从出发到2.2分钟时间段,甲队的速度比乙队的速度快,故原说法错误;
故答案为:③.
19.解:由题意得:
甲的速度为:(km/min),
乙的速度为:(km/min),
设乙在甲骑行x分钟时追上甲,根据题意得:
0.2x=0.4(x﹣10),
解得x=20.
所以乙在甲骑行20分钟时追上甲.
故答案为:20.
20.解:由图象可知,
甲的速度逐渐增大,故①说法错误;
乙车第12秒时的速度为32米/秒,故②说法正确;
乙车前4秒行驶的总路程为:12×4=48(米),故③说法正确.
故答案为:②③.
21.解:(1)这种车的油箱最多能装50升油.
(2)加满油后可供该车行驶1000千米.
(3)该车每行驶200千米消耗汽油10升.
(4)油箱中的剩余油量小于10升时,车辆将自动报警,行驶800千米后,车辆将自动报警.
故答案为:(1)50;(2)1000;(3)10;(4)800.
22.解:(1)由图象可知,学校离他家1000米,从出发到学校,王老师共用了25分钟;王老师吃早餐用了20﹣10=10(分钟),
故答案为:1000,25,10;
(2)根据图象可得:王老师吃早餐以前的速度为:(米/分),吃完早餐以后的速度为:(米/分),
50<100,
答:吃完早餐以后的速度快.
23.解:(1)由图象可知,干旱持续到第10天,水库的蓄水量为1200万立方米.
故答案为:1200;
(2)(1500﹣1200)÷10=30(万立方米),
(1500﹣360)÷30=38(天),
答:38天后将发生严重干旱警报;
(3)1500÷30﹣38=12(天),
答:照这样干旱下去,预计再持续12天时,水库将干涸.
24.解:(1)由图象可知,琳琳家离药店的距离为2.5km.
故答案为:2.5;
(2)由图象可知,琳琳邮寄物品用了:65﹣45=20(分钟),
故答案为:20;
(3)从药店步行到邮局的路程为1km,时间为15min,所以速度为km/min;
从邮局步行回家的路程为1.5km,时间为25min,所以速度为:(km/min);
(4)图中点P的意义是:离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.
故答案为:离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.
25.解:(1)由图象可知,小钱开始营业前微信零钱有50元;
(2)由图象可知,销售草莓20kg后,小钱的微信零钱为650元,
∴销售草莓20kg,销售收入为650﹣50=600元,
∴降价前草莓每千克售价为:600÷20=30(元);
(3)降价后草莓每千克售价为:30﹣10=20元,
∴小钱卖完所有草莓微信零钱为:650+5×20=750(元),
答:小钱卖完所有草莓微信零钱应该有750元.
26.解:由图象可知:
(1)甲先到达终点,先到5分钟;
(2)甲的行驶速度为:6÷(25﹣5)=0.3(千米/分);
乙的行驶速度为:6÷30=0.2(千米/分);
(3)在乙出发后5分钟到25分钟,两人均行驶在途中;
(4)当甲、乙两人途中相遇时,相遇地与A地的距离为3千米.
27.解:(1)由函数图象得:
最先到达终点的是乙队,比另一队领先6﹣5=1分钟到达.
故答案为:乙,1;
(2)由函数图象得:
甲的速度为:900÷6=150米/分,而乙队在第2分钟后第一次加速,其速度为(500﹣200)÷2=150米/分,第4分钟后第二次加速.
故答案为:150,2,150,4;
(3)乙队在第一次加速后,始终保持这个速度继续前进走完余下路程需要的时间为
700÷150=,
∴乙队走完全程的时间为分钟.
∵甲队行驶完全程需要的时间是6分钟.,
∴甲先到达终点
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
