2020-2021学年七年级数学青岛版下册《第8章 角》单元综合能力提升训练(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学青岛版下册《第8章 角》单元综合能力提升训练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 190.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 10:10:28 | ||
图片预览




文档简介
2020-2021年度青岛版七年级数学下册《第8章
角》单元综合能力提升训练(附答案)
1.以下四个语句中,正确的有( )
①如果线段AB=BC,则B是线段AC的中点;
②两点之间直线最短;
③大于直角的角是钝角;
④如图,∠ABD也可用∠B表示.
A.0个
B.1个
C.2个
D.3个
2.上午8点整时,钟表表面的时针与分针的夹角是( )
A.30°
B.45°
C.90°
D.120°
3.钟表上2时25分时,时针与分针所成的角是( )
A.77.5°
B.77°5′
C.75°
D.以上答案都不对
4.如图,某边防战士驾驶摩托艇外出巡逻,先从港口A点沿北偏东60°的方向行驶30海里到达B点,再从B点沿北偏西30°方向行驶30海里到C点,要想从C点直接回到港口A,行驶的方向应是( )
A.南偏西15°方向
B.南偏西60°方向
C.南偏西30°方向
D.南偏西45°方向
5.如图∠AOB=60°,射线OC平分∠AOB,以OC为一边作∠COP=15°,则∠BOP=( )
A.15°
B.45°
C.15°或30°
D.15°或45°
6.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为( )
A.5
B.4
C.5或23
D.4或22
7.将两个完全相同的直角三角板按如图所示的方式放置,若∠BCD=28°30',则下列结论错误的是( )
A.∠ACD=118°30'
B.∠ACD=∠BCE
C.∠ACE=151°30'
D.∠ACE﹣∠BCD=120°
8.如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )
A.∠AOD+∠BOE=60°
B.∠AOD=∠EOC
C.∠BOE=2∠COD
D.∠DOE的度数不能确定
9.如图,∠AOB=∠COD=90°,∠COB=58°,则∠DOA的度数是( )
A.102°
B.112°
C.122°
D.142°
10.在∠AOB的内部任取一点C,作射线OC,则一定存在( )
A.∠AOB>∠AOC
B.∠AOB<∠BOC
C.∠BOC>∠AOC
D.∠AOC>∠BOC
11.现在的时间是9时20分,此时钟面上时针与分针夹角的度数是
度.
12.计算:48°39′+67°31′=
.
13.如图,点A、O、B在一条直线上,∠AOC=130°,OD是∠BOC的平分线,则∠COD=
度.
14.如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=50°,∠BOE=∠BOC,∠BOD=∠AOB,则∠DOE=
°(用含n的代数式表示).
15.已知∠α=32°,则∠α的补角为
度.
16.比较大小:52°52′
52.52°.(填“>”、“<”或“=”)
17.观察图形,并阅读相关的文字,回答:10条直线相交,最多有
交点.
18.如图,∠AOC为平角,已知OE平分∠AOB,OF平分∠BOC,AC与DF相交于点O,∠AOD=25°,则∠BOE的度数为
.
19.如图,直线AB,CD相交于点O,EO⊥AB于点O,若∠AOD=132°,则∠EOC=
°.
20.如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是
.
21.点O是直线AB上一点,以O为端点画射线OC,OD,使∠AOC=60°,∠COD=90°,画出符合题意的两个图形,再求∠BOD的度数.
22.填空,完成下列说理过程
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
23.在∠AOB和∠COD中,
(1)如图1,已知∠AOB=∠COD=90°,当∠BOD=40°时,求∠AOC的度数;
(2)如图2,已知∠AOB=82°,∠COD=110°,且∠AOC=2∠BOD时,请直接写出∠BOD的度数;
(3)如图3,当∠AOB=α,∠COD=β,且∠AOC=n∠BOD(n>1)时,请直接用含有α,β,n的代数式表示∠BOD的值.
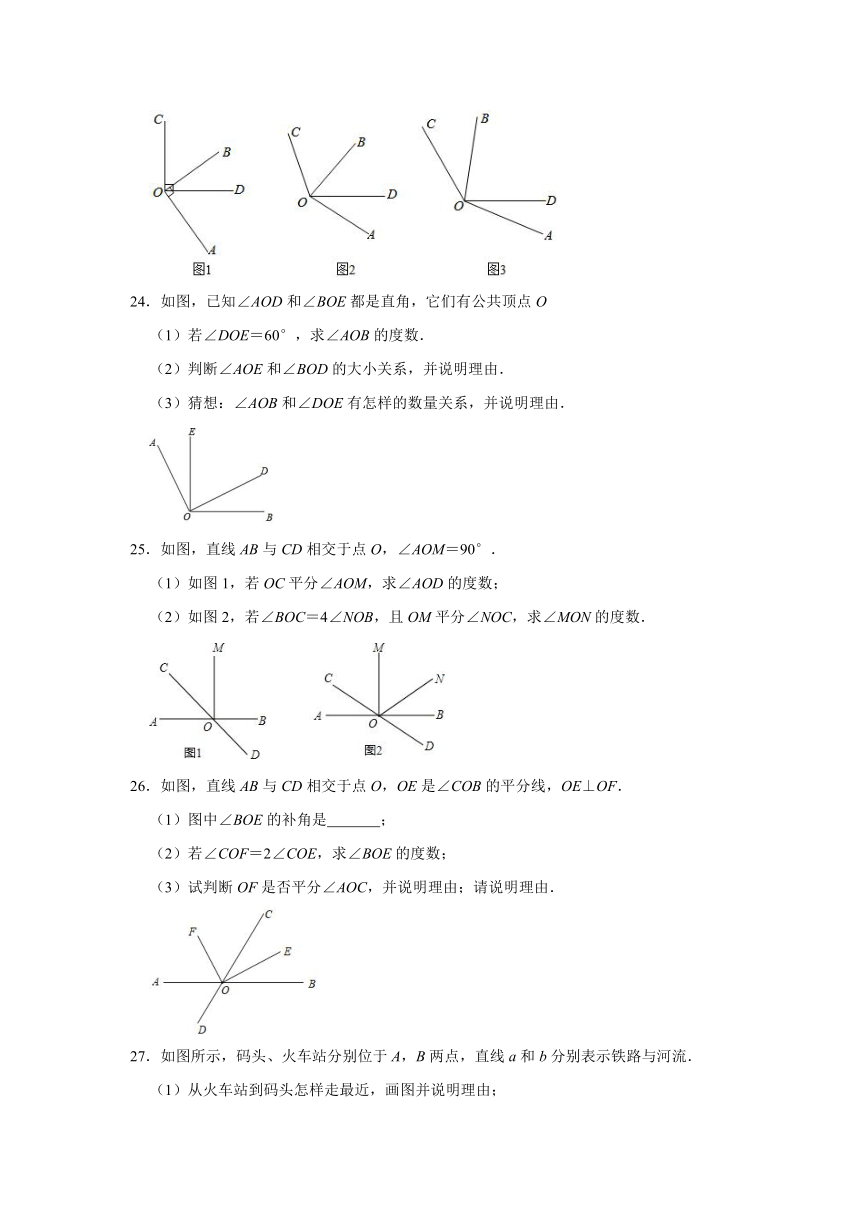
24.如图,已知∠AOD和∠BOE都是直角,它们有公共顶点O
(1)若∠DOE=60°,求∠AOB的度数.
(2)判断∠AOE和∠BOD的大小关系,并说明理由.
(3)猜想:∠AOB和∠DOE有怎样的数量关系,并说明理由.
25.如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
26.如图,直线AB与CD相交于点O,OE是∠COB的平分线,OE⊥OF.
(1)图中∠BOE的补角是
;
(2)若∠COF=2∠COE,求∠BOE的度数;
(3)试判断OF是否平分∠AOC,并说明理由;请说明理由.
27.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
参考答案
1.解:①如果线段AB=BC,则B是线段AC的中点,说法错误,必须说明A、B、C三点共线时;
②两点之间直线最短,说法错误,应是两点之间线段最短;
③大于直角的角是钝角说法错误,应该是大于直角小于平角的角是钝角;
④如图,∠ABD也可用∠B表示,说法错误,以B为顶点的角不是一个,故不能用∠B表示,
故选:A.
2.解:如图,上午8点整时,钟表表面的时针与分针的夹角是4×30°=120°
故选:D.
3.解:我们把时针指向2,分针指向12作为起始位置,
当分针指向25时,他转了25×6°=150°,
此时时针转动了150°×=12.5°,
则时针和3之间还有30°﹣12.5°=17.5°,
故时针和分针之间夹角为30°×2+17.5°=77.5°.
故选:A.
4.解:如图,由题可得,∠BAF=60°,∠CBE=30°,AF∥BE,
∴∠ABC=90°,
又∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠BCA=45°,
又∵∠BCD=∠CBE=30°,
∴∠ACD=15°,
∴从C点直接回到港口A,行驶的方向应是南偏西15°方向,
故选:A.
5.解:∵∠AOB=60°,射线OC平分∠AOB,
∴∠AOC=∠BOC=AOB=30°,
又∠COP=15°
①当OP在∠BOC内,
∠BOP=∠BOC﹣∠COP=30°﹣15°=15°,
②当OP在∠AOC内,
∠BOP=∠BOC+∠COP=30°+15°=45°,
综上所述:∠BOP=15°或45°.
故选:D.
6.解:∵∠BOC=100°,
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,如下图:
∠BON=∠AOC=40°,
此时,三角板旋转的角度为90°﹣40°=50°,
∴t=50°÷10°=5;
当ON在∠AOC的内部时,如下图:
三角板旋转的角度为360°﹣90°﹣40°=230°,
∴t=230°÷10°=23;
∴t的值为:5或23.
故选:C.
7.解:A.因为∠ACD=∠ACB+∠BCD=90°+28°30′=118°30′,
所以选项A不符合题意;
B.因为∠ACD=∠ACB+∠BCD=90°+28°30′=118°30′,
∠BCE=∠DCE+∠BCD=90°+28°30′=118°30′,
所以∠ACD=∠BCE,
所以B选项不符合题意;
C.因为∠ACE=360°﹣90°﹣90°﹣28°30′=151°30',
所以C选项不符合题意;
D.因为∠ACE﹣∠BCD=151°30′﹣28°30′=122°,
所以D选项错误,符合题意.
故选:D.
8.解:如图所示:
∵OD,OE分别是∠AOC,∠BOC的角平分线,
∴∠AOD=∠DOC=,
∠COE=∠BOE=,
又∵∠AOB=∠AOC+∠BOC=120°,
∴∠AOD+∠BOE=60°,
故选:A.
9.解:∵∠AOB=∠COD=90°,∠COB=58°,
∴∠BOD=∠COA=90°﹣58°=32°,
∴∠DOA=∠AOB+∠DOB=90°+32°=122°.
故选:C.
10.解:射线OC在∠AOB的内部,那么∠AOC在∠AOB的内部,且有一公共边;
则一定存在∠AOB>∠AOC.
故选:A.
11.解:∵“4”至“9”的夹角为30°×5=150°,时针偏离“9”的度数为30°×=10°,
∴时针与分针的夹角应为150°+10°=160°.
12.解:39′+31′=70′=1°10′,
故48°39′+67°31′=116°10'.
故答案为:116°10'.
13.解:∵点A、O、B在一条直线上,∠AOC=130°,
∴∠COB=180°﹣130°=50°,
∵OD是∠BOC的平分线,
∴∠COD=∠BOC=25°.
故答案为:25.
14.解:∵∠BOE=∠BOC,
∴∠BOC=n∠BOE,
∴∠AOB=∠AOC+∠BOC=50°+n∠BOE,
∴∠BOD=∠AOB=+∠BOE,
∴∠DOE=∠BOD﹣∠BOE=,
故答案为:.
15.解:∵∠α=32°,
∴∠α的补角为:180°﹣32°=148°.
故答案为:148.
16.解:∵0.52×60=31.2,0.2×60=12,
∴52.52°=52°31′12″,
52°52′>52°31′12″,
故答案为:>.
17.解:∵10条直线两两相交:3条直线相交最多有3个交点,4条直线相交最多有6个交点,
5条直线相交最多有10个交点,而3=×2×3,6=×3×4,10=1+2+3+4=×4×5,
∴十条直线相交最多有交点的个数是:n(n﹣1)=×10×9=45.
故答案为:45.
18.解:∵OE平分∠AOB,OF平分∠BOC,
∴∠AOE=∠EOB=∠AOB,∠COF=∠BOF=∠BOC,
∵∠AOC为平角,
∴∠AOB+∠BOC=180°
∴∠EOB+∠BOF=∠EOF=90°
∵∠AOD=25°=∠COF,
∴∠BOE=90°﹣25°=65°,
故答案为:65°.
19.解:∵∠AOD=132°,
∴∠COB=132°,
∵EO⊥AB,
∴∠EOB=90°,
∴∠COE=132°﹣90°=42°,
故答案为:42.
20.解:先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短;
故答案为:垂线段最短.
21.解:满足题意的情况有两种:
①当OC,OD在AB的同侧时,如图,∠BOD=180°﹣∠AOC﹣∠COD=30°;
②当OC,OD在AB的异侧时,如图,∠BOD=180°﹣(∠COD﹣∠AOC)=150°;
22.解:(1)如图,∵OD是∠AOC的平分线,
∴∠COD=∠AOC.
∵OE是∠BOC的平分线,
∴∠COE=∠BOC.
所以∠DOE=∠COD+∠COE=(∠AOC+∠BOC)=∠AOB=90°.
(2)由(1)可知:
∠BOE=∠COE=90°﹣∠COD=25°.
所以∠AOE=180°﹣∠BOE=155°.
23.解:(1)如图1,∵∠AOB=∠COD=90°,∠BOD=40°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣40°=140°,
答:∠AOC的度数为140°;
(2)如图2,∵∠AOB=82°,∠COD=110°,
∴∠AOC=∠AOB+∠COD﹣∠BOD
=82°+110°﹣∠BOD,
又∵∠AOC=2∠BOD,
∴2∠BOD=82°+110°﹣∠BOD,
∴∠BOD==64°,
答:∠BOD的度数为64°;
(3)如图3,∵∠AOB=α,∠COD=β,
∴∠AOC=∠AOB+∠COD﹣∠BOD
=α+β﹣∠BOD,
又∵∠AOC=n∠BOD,
∴n∠BOD=α+β﹣∠BOD,
∴∠BOD=,
答:∠BOD=.
24.解:(1)因为∠AOD和∠BOE都是直角
∠DOE=60°,
所以∠AOE=∠AOD﹣∠DOE=90°﹣60°=30°
所以∠AOB=∠AOE+∠BOE=30°+90°=120°
答:∠AOB的度数为120°.
(2)∠AOE和∠BOD的大小关系是相等,理由如下:
因为∠AOD和∠BOE都是直角
所以∠AOE=∠AOD﹣∠DOE=90°﹣∠DOE
∠BOD=∠BOE﹣∠DOE=90°﹣∠DOE
所以∠AOE=∠BOD.
(3)∠AOB+∠DOE=180°.理由如下:
因为∠AOB=∠AOD+∠DOB=90°+∠DOB
所以∠DOB=∠AOB﹣90°
因为∠DOE=∠BOE﹣∠DOB=90°﹣∠DOB
所以∠DOB=90°﹣∠DOE
所以∠AOB﹣90°=90°﹣∠DOE
所以∠AOB+∠DOE=180°.
25.解(1)∵∠AOM=90°,OC平分∠AOM,
∴∠AOC=∠AOM=×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°﹣∠AOC=180°﹣45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB﹣∠BON=4x°﹣x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=∠CON=x°,
∵∠BOM=x+x=90°,
∴x=36°,
∴∠MON=x°=×36°=54°,
即∠MON的度数为54°.
26.解:(1)∵∠AOE+∠BOE=∠AOB=180°,∠COE+∠DOE=∠COD=180°,∠COE=∠BOE
∴∠BOE的补角是∠AOE,∠DOE
故答案为:∠AOE或∠DOE;
(2)∵OE⊥OF.∠COF=2∠COE,
∴∠COF=×90°=60°,∠COE=×90°=30°,
∵OE是∠COB的平分线,
∴∠BOE=∠COE=30°;
(3)OF平分∠AOC,
∵OE是∠COB的平分线,OE⊥OF.
∴∠BOE=∠COE,∠COE+∠COF=90°,
∵∠BOE+∠EOC+∠COF+∠FOA=180°,
∴∠COE+∠FOA=90°,
∴∠FOA=∠COF,
即,OF平分∠AOC.
27.解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
角》单元综合能力提升训练(附答案)
1.以下四个语句中,正确的有( )
①如果线段AB=BC,则B是线段AC的中点;
②两点之间直线最短;
③大于直角的角是钝角;
④如图,∠ABD也可用∠B表示.
A.0个
B.1个
C.2个
D.3个
2.上午8点整时,钟表表面的时针与分针的夹角是( )
A.30°
B.45°
C.90°
D.120°
3.钟表上2时25分时,时针与分针所成的角是( )
A.77.5°
B.77°5′
C.75°
D.以上答案都不对
4.如图,某边防战士驾驶摩托艇外出巡逻,先从港口A点沿北偏东60°的方向行驶30海里到达B点,再从B点沿北偏西30°方向行驶30海里到C点,要想从C点直接回到港口A,行驶的方向应是( )
A.南偏西15°方向
B.南偏西60°方向
C.南偏西30°方向
D.南偏西45°方向
5.如图∠AOB=60°,射线OC平分∠AOB,以OC为一边作∠COP=15°,则∠BOP=( )
A.15°
B.45°
C.15°或30°
D.15°或45°
6.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为( )
A.5
B.4
C.5或23
D.4或22
7.将两个完全相同的直角三角板按如图所示的方式放置,若∠BCD=28°30',则下列结论错误的是( )
A.∠ACD=118°30'
B.∠ACD=∠BCE
C.∠ACE=151°30'
D.∠ACE﹣∠BCD=120°
8.如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )
A.∠AOD+∠BOE=60°
B.∠AOD=∠EOC
C.∠BOE=2∠COD
D.∠DOE的度数不能确定
9.如图,∠AOB=∠COD=90°,∠COB=58°,则∠DOA的度数是( )
A.102°
B.112°
C.122°
D.142°
10.在∠AOB的内部任取一点C,作射线OC,则一定存在( )
A.∠AOB>∠AOC
B.∠AOB<∠BOC
C.∠BOC>∠AOC
D.∠AOC>∠BOC
11.现在的时间是9时20分,此时钟面上时针与分针夹角的度数是
度.
12.计算:48°39′+67°31′=
.
13.如图,点A、O、B在一条直线上,∠AOC=130°,OD是∠BOC的平分线,则∠COD=
度.
14.如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=50°,∠BOE=∠BOC,∠BOD=∠AOB,则∠DOE=
°(用含n的代数式表示).
15.已知∠α=32°,则∠α的补角为
度.
16.比较大小:52°52′
52.52°.(填“>”、“<”或“=”)
17.观察图形,并阅读相关的文字,回答:10条直线相交,最多有
交点.
18.如图,∠AOC为平角,已知OE平分∠AOB,OF平分∠BOC,AC与DF相交于点O,∠AOD=25°,则∠BOE的度数为
.
19.如图,直线AB,CD相交于点O,EO⊥AB于点O,若∠AOD=132°,则∠EOC=
°.
20.如图,计划把水从河中引到水池A中,先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是
.
21.点O是直线AB上一点,以O为端点画射线OC,OD,使∠AOC=60°,∠COD=90°,画出符合题意的两个图形,再求∠BOD的度数.
22.填空,完成下列说理过程
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
23.在∠AOB和∠COD中,
(1)如图1,已知∠AOB=∠COD=90°,当∠BOD=40°时,求∠AOC的度数;
(2)如图2,已知∠AOB=82°,∠COD=110°,且∠AOC=2∠BOD时,请直接写出∠BOD的度数;
(3)如图3,当∠AOB=α,∠COD=β,且∠AOC=n∠BOD(n>1)时,请直接用含有α,β,n的代数式表示∠BOD的值.
24.如图,已知∠AOD和∠BOE都是直角,它们有公共顶点O
(1)若∠DOE=60°,求∠AOB的度数.
(2)判断∠AOE和∠BOD的大小关系,并说明理由.
(3)猜想:∠AOB和∠DOE有怎样的数量关系,并说明理由.
25.如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
26.如图,直线AB与CD相交于点O,OE是∠COB的平分线,OE⊥OF.
(1)图中∠BOE的补角是
;
(2)若∠COF=2∠COE,求∠BOE的度数;
(3)试判断OF是否平分∠AOC,并说明理由;请说明理由.
27.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
参考答案
1.解:①如果线段AB=BC,则B是线段AC的中点,说法错误,必须说明A、B、C三点共线时;
②两点之间直线最短,说法错误,应是两点之间线段最短;
③大于直角的角是钝角说法错误,应该是大于直角小于平角的角是钝角;
④如图,∠ABD也可用∠B表示,说法错误,以B为顶点的角不是一个,故不能用∠B表示,
故选:A.
2.解:如图,上午8点整时,钟表表面的时针与分针的夹角是4×30°=120°
故选:D.
3.解:我们把时针指向2,分针指向12作为起始位置,
当分针指向25时,他转了25×6°=150°,
此时时针转动了150°×=12.5°,
则时针和3之间还有30°﹣12.5°=17.5°,
故时针和分针之间夹角为30°×2+17.5°=77.5°.
故选:A.
4.解:如图,由题可得,∠BAF=60°,∠CBE=30°,AF∥BE,
∴∠ABC=90°,
又∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠BCA=45°,
又∵∠BCD=∠CBE=30°,
∴∠ACD=15°,
∴从C点直接回到港口A,行驶的方向应是南偏西15°方向,
故选:A.
5.解:∵∠AOB=60°,射线OC平分∠AOB,
∴∠AOC=∠BOC=AOB=30°,
又∠COP=15°
①当OP在∠BOC内,
∠BOP=∠BOC﹣∠COP=30°﹣15°=15°,
②当OP在∠AOC内,
∠BOP=∠BOC+∠COP=30°+15°=45°,
综上所述:∠BOP=15°或45°.
故选:D.
6.解:∵∠BOC=100°,
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,如下图:
∠BON=∠AOC=40°,
此时,三角板旋转的角度为90°﹣40°=50°,
∴t=50°÷10°=5;
当ON在∠AOC的内部时,如下图:
三角板旋转的角度为360°﹣90°﹣40°=230°,
∴t=230°÷10°=23;
∴t的值为:5或23.
故选:C.
7.解:A.因为∠ACD=∠ACB+∠BCD=90°+28°30′=118°30′,
所以选项A不符合题意;
B.因为∠ACD=∠ACB+∠BCD=90°+28°30′=118°30′,
∠BCE=∠DCE+∠BCD=90°+28°30′=118°30′,
所以∠ACD=∠BCE,
所以B选项不符合题意;
C.因为∠ACE=360°﹣90°﹣90°﹣28°30′=151°30',
所以C选项不符合题意;
D.因为∠ACE﹣∠BCD=151°30′﹣28°30′=122°,
所以D选项错误,符合题意.
故选:D.
8.解:如图所示:
∵OD,OE分别是∠AOC,∠BOC的角平分线,
∴∠AOD=∠DOC=,
∠COE=∠BOE=,
又∵∠AOB=∠AOC+∠BOC=120°,
∴∠AOD+∠BOE=60°,
故选:A.
9.解:∵∠AOB=∠COD=90°,∠COB=58°,
∴∠BOD=∠COA=90°﹣58°=32°,
∴∠DOA=∠AOB+∠DOB=90°+32°=122°.
故选:C.
10.解:射线OC在∠AOB的内部,那么∠AOC在∠AOB的内部,且有一公共边;
则一定存在∠AOB>∠AOC.
故选:A.
11.解:∵“4”至“9”的夹角为30°×5=150°,时针偏离“9”的度数为30°×=10°,
∴时针与分针的夹角应为150°+10°=160°.
12.解:39′+31′=70′=1°10′,
故48°39′+67°31′=116°10'.
故答案为:116°10'.
13.解:∵点A、O、B在一条直线上,∠AOC=130°,
∴∠COB=180°﹣130°=50°,
∵OD是∠BOC的平分线,
∴∠COD=∠BOC=25°.
故答案为:25.
14.解:∵∠BOE=∠BOC,
∴∠BOC=n∠BOE,
∴∠AOB=∠AOC+∠BOC=50°+n∠BOE,
∴∠BOD=∠AOB=+∠BOE,
∴∠DOE=∠BOD﹣∠BOE=,
故答案为:.
15.解:∵∠α=32°,
∴∠α的补角为:180°﹣32°=148°.
故答案为:148.
16.解:∵0.52×60=31.2,0.2×60=12,
∴52.52°=52°31′12″,
52°52′>52°31′12″,
故答案为:>.
17.解:∵10条直线两两相交:3条直线相交最多有3个交点,4条直线相交最多有6个交点,
5条直线相交最多有10个交点,而3=×2×3,6=×3×4,10=1+2+3+4=×4×5,
∴十条直线相交最多有交点的个数是:n(n﹣1)=×10×9=45.
故答案为:45.
18.解:∵OE平分∠AOB,OF平分∠BOC,
∴∠AOE=∠EOB=∠AOB,∠COF=∠BOF=∠BOC,
∵∠AOC为平角,
∴∠AOB+∠BOC=180°
∴∠EOB+∠BOF=∠EOF=90°
∵∠AOD=25°=∠COF,
∴∠BOE=90°﹣25°=65°,
故答案为:65°.
19.解:∵∠AOD=132°,
∴∠COB=132°,
∵EO⊥AB,
∴∠EOB=90°,
∴∠COE=132°﹣90°=42°,
故答案为:42.
20.解:先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短;
故答案为:垂线段最短.
21.解:满足题意的情况有两种:
①当OC,OD在AB的同侧时,如图,∠BOD=180°﹣∠AOC﹣∠COD=30°;
②当OC,OD在AB的异侧时,如图,∠BOD=180°﹣(∠COD﹣∠AOC)=150°;
22.解:(1)如图,∵OD是∠AOC的平分线,
∴∠COD=∠AOC.
∵OE是∠BOC的平分线,
∴∠COE=∠BOC.
所以∠DOE=∠COD+∠COE=(∠AOC+∠BOC)=∠AOB=90°.
(2)由(1)可知:
∠BOE=∠COE=90°﹣∠COD=25°.
所以∠AOE=180°﹣∠BOE=155°.
23.解:(1)如图1,∵∠AOB=∠COD=90°,∠BOD=40°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣40°=140°,
答:∠AOC的度数为140°;
(2)如图2,∵∠AOB=82°,∠COD=110°,
∴∠AOC=∠AOB+∠COD﹣∠BOD
=82°+110°﹣∠BOD,
又∵∠AOC=2∠BOD,
∴2∠BOD=82°+110°﹣∠BOD,
∴∠BOD==64°,
答:∠BOD的度数为64°;
(3)如图3,∵∠AOB=α,∠COD=β,
∴∠AOC=∠AOB+∠COD﹣∠BOD
=α+β﹣∠BOD,
又∵∠AOC=n∠BOD,
∴n∠BOD=α+β﹣∠BOD,
∴∠BOD=,
答:∠BOD=.
24.解:(1)因为∠AOD和∠BOE都是直角
∠DOE=60°,
所以∠AOE=∠AOD﹣∠DOE=90°﹣60°=30°
所以∠AOB=∠AOE+∠BOE=30°+90°=120°
答:∠AOB的度数为120°.
(2)∠AOE和∠BOD的大小关系是相等,理由如下:
因为∠AOD和∠BOE都是直角
所以∠AOE=∠AOD﹣∠DOE=90°﹣∠DOE
∠BOD=∠BOE﹣∠DOE=90°﹣∠DOE
所以∠AOE=∠BOD.
(3)∠AOB+∠DOE=180°.理由如下:
因为∠AOB=∠AOD+∠DOB=90°+∠DOB
所以∠DOB=∠AOB﹣90°
因为∠DOE=∠BOE﹣∠DOB=90°﹣∠DOB
所以∠DOB=90°﹣∠DOE
所以∠AOB﹣90°=90°﹣∠DOE
所以∠AOB+∠DOE=180°.
25.解(1)∵∠AOM=90°,OC平分∠AOM,
∴∠AOC=∠AOM=×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°﹣∠AOC=180°﹣45°=135°,
即∠AOD的度数为135°;
(2)∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°,
∴∠CON=∠COB﹣∠BON=4x°﹣x°=3x°,
∵OM平分∠CON,
∴∠COM=∠MON=∠CON=x°,
∵∠BOM=x+x=90°,
∴x=36°,
∴∠MON=x°=×36°=54°,
即∠MON的度数为54°.
26.解:(1)∵∠AOE+∠BOE=∠AOB=180°,∠COE+∠DOE=∠COD=180°,∠COE=∠BOE
∴∠BOE的补角是∠AOE,∠DOE
故答案为:∠AOE或∠DOE;
(2)∵OE⊥OF.∠COF=2∠COE,
∴∠COF=×90°=60°,∠COE=×90°=30°,
∵OE是∠COB的平分线,
∴∠BOE=∠COE=30°;
(3)OF平分∠AOC,
∵OE是∠COB的平分线,OE⊥OF.
∴∠BOE=∠COE,∠COE+∠COF=90°,
∵∠BOE+∠EOC+∠COF+∠FOA=180°,
∴∠COE+∠FOA=90°,
∴∠FOA=∠COF,
即,OF平分∠AOC.
27.解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
