2020-2021学年人教版八年级数学下册:18.1.2平行四边形的判定 课件(共20张ppt)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册:18.1.2平行四边形的判定 课件(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 910.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 20:40:20 | ||
图片预览



文档简介
(共20张PPT)
平行四边形的判定
B
D
C
A
2、什么样的四边形是平行四边形?
1、平行四边形的性质有哪些?
回顾与思考
学习目标
能够证明平行四边形的判定定理.
体会在证明过程中所运用的类比、转化、归纳等数学思想方法.
自主学习
1、自学课本内容
2、四人一组合作完成四个定理的证明
平行四边形的判定
定理:两组对边分别相等的四边形是平行四边形.
B
D
C
A
已知:如图,在四边形ABCD中,AB=CD,BC=DA..
求证:四边形ABCD是平行四边形.
自我展示1
B
D
C
A
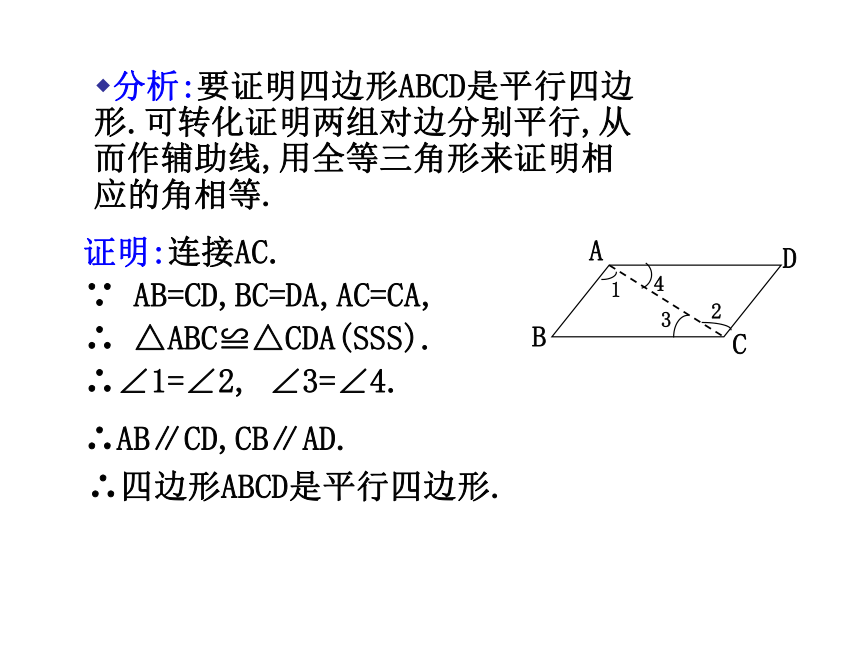
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行,从而作辅助线,用全等三角形来证明相应的角相等.
证明:连接AC.
∵
AB=CD,BC=DA,AC=CA,
∴
△ABC≌△CDA(SSS).
∴∠1=∠2,
∠3=∠4.
∴AB∥CD,CB∥AD.
∴四边形ABCD是平行四边形.
1
2
3
4
定理:一组对边平行且相等的四边形是平行四边形.
已知:如图,在四边形ABCD中
AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
B
D
C
A
自我展示2
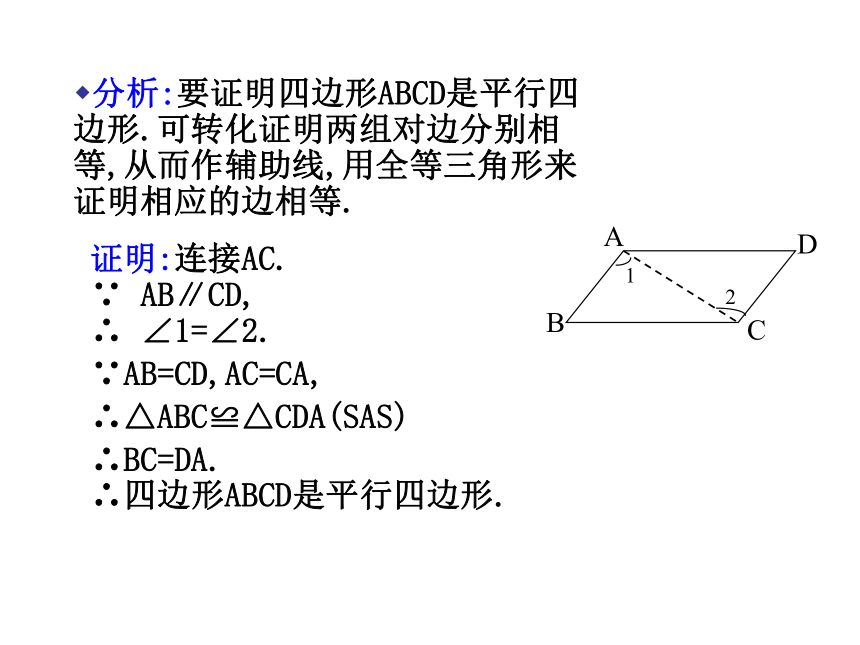
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别相等,从而作辅助线,用全等三角形来证明相应的边相等.
证明:连接AC.
∵
AB∥CD,
∴
∠1=∠2.
∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS)
∴四边形ABCD是平行四边形.
∴BC=DA.
B
D
C
A
1
2
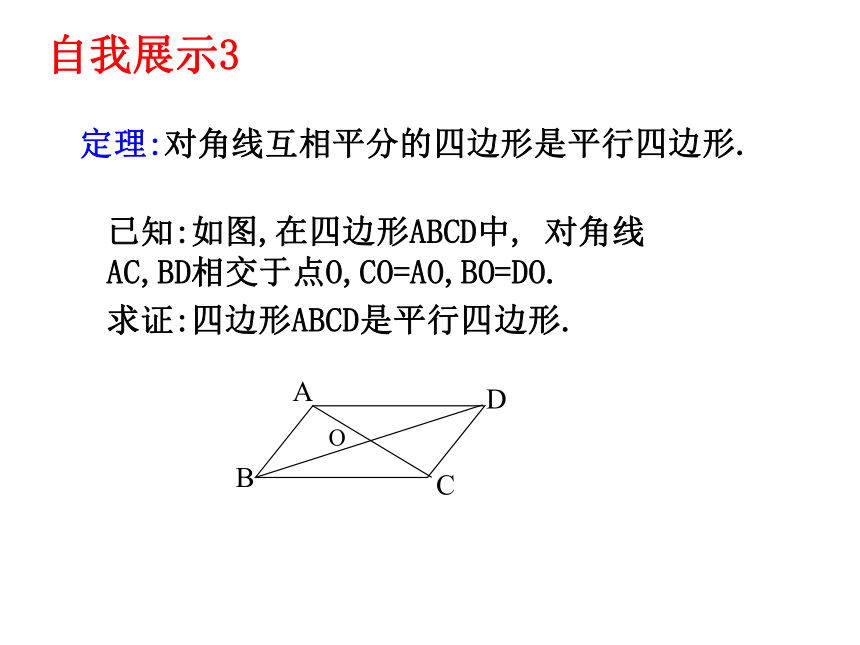
定理:对角线互相平分的四边形是平行四边形.
已知:如图,在四边形ABCD中,
对角线AC,BD相交于点O,CO=AO,BO=DO.
求证:四边形ABCD是平行四边形.
B
D
C
A
O
自我展示3
证明:
∵CO=AO,BO=DO,∠1=∠2,
∴△AOD≌△COB(SAS).
∴∠3=∠4.
∴AD∥CB.
同理,AB∥CD.
∴四边形ABCD是平行四边形.
B
D
C
A
O
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行,从而用全等三角形来证明相应的角相等.
4
3
2
1
定理:两组对角分别相等的四边形是平行四边形的.
已知:如图,在四边形ABCD中∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
B
D
C
A
自我展示4
①有一组对边平行的四边形是平行四边形。
②有两条边相等,并且另外的两条边也相等的四边形一定
是平行四边形。
③对角线相等的四边形是平行四边形。
④一条对角线平分另一条对角线的四边形是平行四边形。
1.判断
2.
任选教室里不坐在同一直线上的三个同学作为一个平行四边形的三个顶点,那么第四个顶点是哪个座位的同学,请你站起来。
全体总动员
1.已知:如图
求证:四边形MNOP是平行四边形.
分析:这是一道综合性题目,利用勾股定理,方程和平行四边形的判定进行计算性推理可获证.
证明:
O
M
N
P
4
5
x-3
11-x
x-5
∴四边形MNPO是平行四边形.
试一试
判定
文字语言
图形语言
符号语言
方法1
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是…
方法2
两组对边分别相等的四边形是平行四边形
∵AB=CD,
AD=
BC
∴…是…
方法3
一组对边平行且相等的四边形是平行四边形
∵AB=CD
AB∥CD,
∴…是…
方法4
对角线互相平分的四边形是平行四边形
∵AC、BD交于点,OA=OC,
OB=OD
∴…是…
方法5
两组对角分别相等的四边形是平行四边形
∵∠A=∠C,
∠B=∠D
∴…是…
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
谈谈本节课你有哪些收获?
课堂小结
1.如图,在□ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.
链接中考
2.已知:如图,在□ABCD中,∠ABC的平分线与AD相交于点P.
求证:PD+CD=BC.
D
B
C
A
P
分析:要证明两条线段的和等于另一条线段,可以将BC分割为两部分,来证明相应的线段相等.如将CD平移(过P作CD的平行线)到PE的位置,则可利用等角对等边来证明PE=BE,从而问题得证.
证明:过点P作PE∥CD,交BC于点E.
∵四边形ABCD是平行四边形,
∴PE∥CD∥AB,
∴
∠1=∠3,
四边形PDCE是平行四边形.
∵
∠1=∠2.
∴∠3=∠2.
∴PE=BE.
∴AB∥CD,AD∥BC.
∴PD+CD=BE+EC=BC.
D
B
C
A
P
3
1
E
1
2
∴
PD=EC,PE=CD.
【证明】∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD,
∴∠BAE=∠DCF,
∵AE=CF,
∴△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形BEDF是平行四边形,
∴∠EBF=∠FDE.
平行四边形的判定
B
D
C
A
2、什么样的四边形是平行四边形?
1、平行四边形的性质有哪些?
回顾与思考
学习目标
能够证明平行四边形的判定定理.
体会在证明过程中所运用的类比、转化、归纳等数学思想方法.
自主学习
1、自学课本内容
2、四人一组合作完成四个定理的证明
平行四边形的判定
定理:两组对边分别相等的四边形是平行四边形.
B
D
C
A
已知:如图,在四边形ABCD中,AB=CD,BC=DA..
求证:四边形ABCD是平行四边形.
自我展示1
B
D
C
A
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行,从而作辅助线,用全等三角形来证明相应的角相等.
证明:连接AC.
∵
AB=CD,BC=DA,AC=CA,
∴
△ABC≌△CDA(SSS).
∴∠1=∠2,
∠3=∠4.
∴AB∥CD,CB∥AD.
∴四边形ABCD是平行四边形.
1
2
3
4
定理:一组对边平行且相等的四边形是平行四边形.
已知:如图,在四边形ABCD中
AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
B
D
C
A
自我展示2
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别相等,从而作辅助线,用全等三角形来证明相应的边相等.
证明:连接AC.
∵
AB∥CD,
∴
∠1=∠2.
∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS)
∴四边形ABCD是平行四边形.
∴BC=DA.
B
D
C
A
1
2
定理:对角线互相平分的四边形是平行四边形.
已知:如图,在四边形ABCD中,
对角线AC,BD相交于点O,CO=AO,BO=DO.
求证:四边形ABCD是平行四边形.
B
D
C
A
O
自我展示3
证明:
∵CO=AO,BO=DO,∠1=∠2,
∴△AOD≌△COB(SAS).
∴∠3=∠4.
∴AD∥CB.
同理,AB∥CD.
∴四边形ABCD是平行四边形.
B
D
C
A
O
分析:要证明四边形ABCD是平行四边形.可转化证明两组对边分别平行,从而用全等三角形来证明相应的角相等.
4
3
2
1
定理:两组对角分别相等的四边形是平行四边形的.
已知:如图,在四边形ABCD中∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
B
D
C
A
自我展示4
①有一组对边平行的四边形是平行四边形。
②有两条边相等,并且另外的两条边也相等的四边形一定
是平行四边形。
③对角线相等的四边形是平行四边形。
④一条对角线平分另一条对角线的四边形是平行四边形。
1.判断
2.
任选教室里不坐在同一直线上的三个同学作为一个平行四边形的三个顶点,那么第四个顶点是哪个座位的同学,请你站起来。
全体总动员
1.已知:如图
求证:四边形MNOP是平行四边形.
分析:这是一道综合性题目,利用勾股定理,方程和平行四边形的判定进行计算性推理可获证.
证明:
O
M
N
P
4
5
x-3
11-x
x-5
∴四边形MNPO是平行四边形.
试一试
判定
文字语言
图形语言
符号语言
方法1
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是…
方法2
两组对边分别相等的四边形是平行四边形
∵AB=CD,
AD=
BC
∴…是…
方法3
一组对边平行且相等的四边形是平行四边形
∵AB=CD
AB∥CD,
∴…是…
方法4
对角线互相平分的四边形是平行四边形
∵AC、BD交于点,OA=OC,
OB=OD
∴…是…
方法5
两组对角分别相等的四边形是平行四边形
∵∠A=∠C,
∠B=∠D
∴…是…
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
谈谈本节课你有哪些收获?
课堂小结
1.如图,在□ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.
链接中考
2.已知:如图,在□ABCD中,∠ABC的平分线与AD相交于点P.
求证:PD+CD=BC.
D
B
C
A
P
分析:要证明两条线段的和等于另一条线段,可以将BC分割为两部分,来证明相应的线段相等.如将CD平移(过P作CD的平行线)到PE的位置,则可利用等角对等边来证明PE=BE,从而问题得证.
证明:过点P作PE∥CD,交BC于点E.
∵四边形ABCD是平行四边形,
∴PE∥CD∥AB,
∴
∠1=∠3,
四边形PDCE是平行四边形.
∵
∠1=∠2.
∴∠3=∠2.
∴PE=BE.
∴AB∥CD,AD∥BC.
∴PD+CD=BE+EC=BC.
D
B
C
A
P
3
1
E
1
2
∴
PD=EC,PE=CD.
【证明】∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD,
∴∠BAE=∠DCF,
∵AE=CF,
∴△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形BEDF是平行四边形,
∴∠EBF=∠FDE.
