2020-2021学年人教版八年级数学下册第十八章平行四边形综合训练(Word版,含答案解析)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册第十八章平行四边形综合训练(Word版,含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 697.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 23:08:18 | ||
图片预览


文档简介
人教版
八年级数学下册
第十八章
平行四边形
综合训练
一、选择题
1.
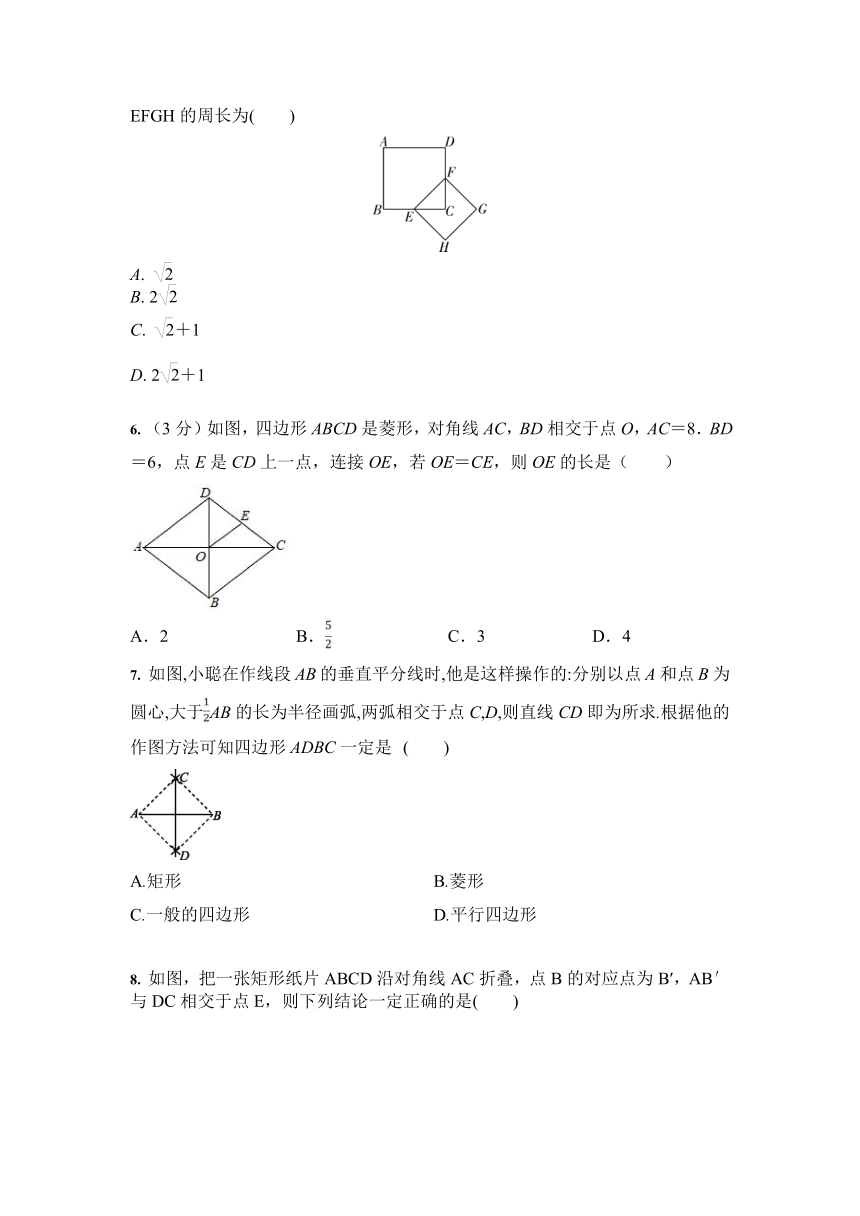
如图,若要使?ABCD成为菱形,则可添加的条件是
( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
2.
如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A.
7
B.
9
C.
10
D.
11
3.
(2020·抚顺本溪辽阳)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,AC=8,BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2
B.
C.3
D.4
4.
(2020·四川甘孜州)如图,菱形ABCD中,对角线AC,BD相交于点O,
E为AB的中点.若菱形ABCD的周长为32,则OE的长为(
)
A.3
B.4
C.5
D.6
5.
如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )
A.
B.
2
C.
+1
D.
2+1
6.
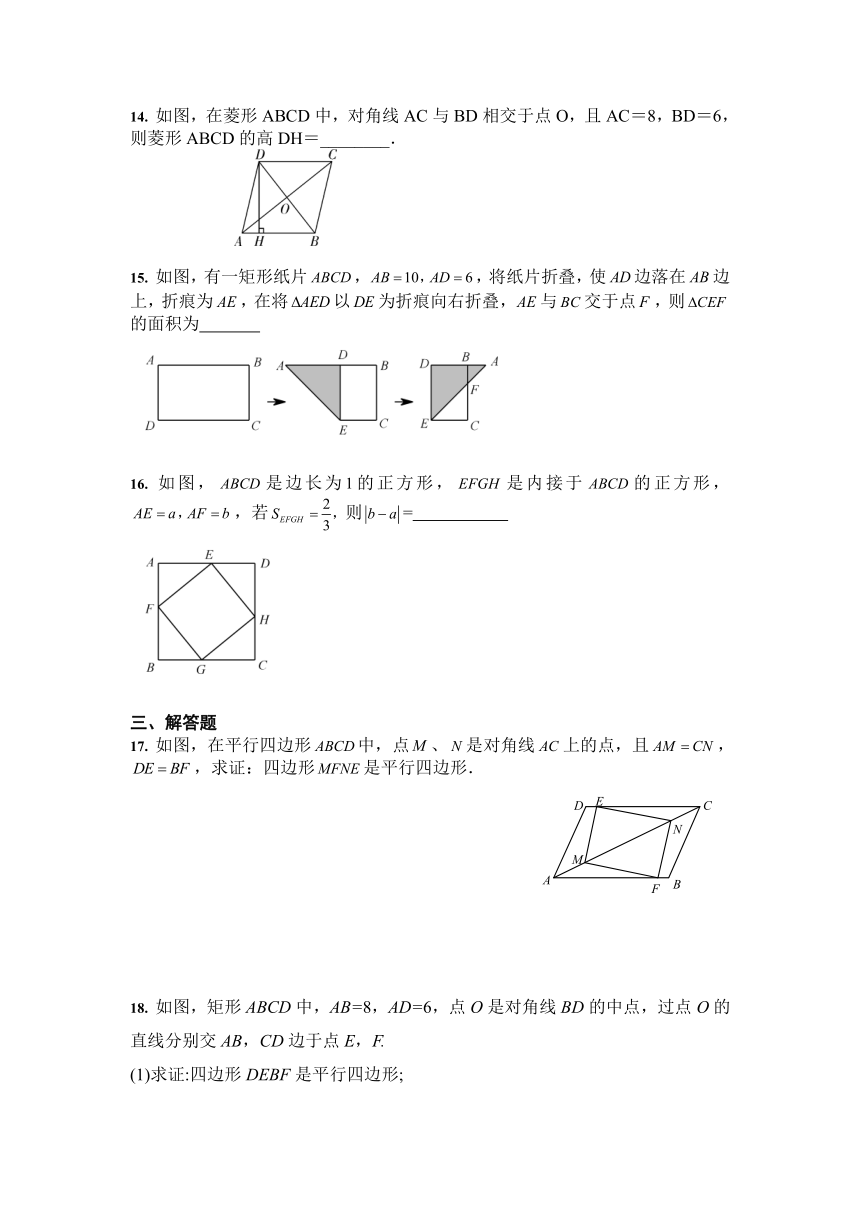
(3分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2
B.
C.3
D.4
7.
如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是
( )
A.矩形
B.菱形
C.一般的四边形
D.平行四边形
8.
如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
二、填空题
9.
在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是
10.
在矩形中,点为的中点,为上任意一点,交于点,交于点,当满足条件
时,四边形是矩形
11.
如图,在平行四边形中,与相交于点,图中共有
个平行四边形
12.
如图,矩形中,相交于点,平分交于,若,求=
13.
如图,已知、分别是正方形的边、上的点,、分别与对角线相交于、,若,则
.
14.
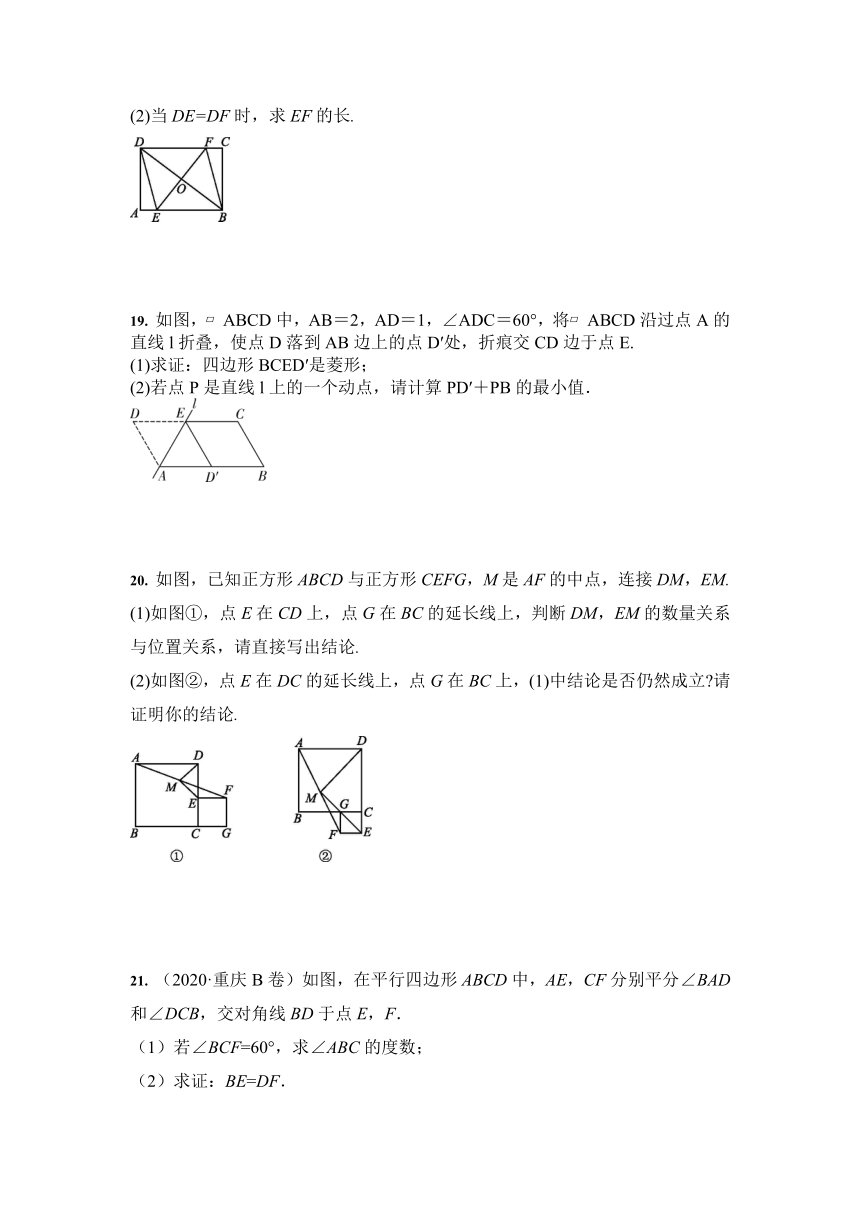
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.
15.
如图,有一矩形纸片,,将纸片折叠,使边落在边上,折痕为,在将以为折痕向右折叠,与交于点,则的面积为
16.
如图,是边长为的正方形,是内接于的正方形,,若则=
三、解答题
17.
如图,在平行四边形中,点、是对角线上的点,且,,求证:四边形是平行四边形.
18.
如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求EF的长.
19.
如图,?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.
20.
如图,已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图①,点E在CD上,点G在BC的延长线上,判断DM,EM的数量关系与位置关系,请直接写出结论.
(2)如图②,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.
21.
(2020·重庆B卷)如图,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠DCB,交对角线BD于点E,F.
(1)若∠BCF=60°,求∠ABC的度数;
(2)求证:BE=DF.
22.
如图,点分别在正方形的边上,已知的周长等于正方形周长的一半,求的度数
23.
如图所示,在正方形中,、是内的两条射线,,,,,求证,.
24.
如图,是平行四边形较长的一条对角线,点是内部一点,于点,于点,于点,求证:.
人教版
八年级数学下册
第十八章
平行四边形
综合训练-答案
一、选择题
1.
【答案】C
2.
【答案】D 【解析】本题考查勾股定理、三角形的中位线定理和四边形的周长
.
解题思路:
?四边形EFGH的周长=EF+FG+HG+EH=11.
3.
【答案】B
【解析】根据菱形对角线互相垂直平分,求出菱形的边长,再结合等腰三角形的性质及判定得出OE=CE=DE,从而求出.∵四边形ABCD是菱形,∴OC=AC=4,
OD=BD=3,
AC⊥DB.∵OE=CE,∴∠EOC=OE∠DCO.∵∠DOE+∠EOC=∠ODC+∠ECO=90°,∴∠DOE=∠ODC,∴OE=DE,∴OE=DC.在Rt△DOC中,CD==5,∴OE=DC=.故选项B正确.
4.
【答案】B
【解析】本题考查了菱形的性质和直角三角形斜边上的中线性质.∵四边形ABCD是菱形,∴AB=BC=CD=DA.∵菱形ABCD的周长为32,∴AB=8.∵AC⊥BD,E为AB的中点,∴OE=AB=4.故选B.
5.
【答案】B 【解析】∵正方形ABCD的面积为1,∴BC=CD=1,∵E、F是边的中点,∴CE=CF=,∴EF==,则正方形EFGH的周长为4×=2.
6.
【答案】B
【解析】根据菱形的对角线互相垂直平分求出OB,OC,AC⊥BD,然后利用勾股定理列式求出BC,最后根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
∵菱形ABCD的对角线AC、BD相交于点O,
∴OBBD6=3,OA=OCAC8=4,AC⊥BD,
由勾股定理得,BC5,
∴AD=5,
∵OE=CE,
∴∠DCA=∠EOC,
∵四边形ABCD是菱形,
∴∠DCA=∠DAC,
∴∠DAC=∠EOC,
∴OE∥AD,
∵AO=OC,
∴OE是△ADC的中位线,
∴OEAD=2.5.
7.
【答案】B
8.
【答案】D 【解析】∵四边形ABCD为矩形,∴AB∥CD,∴∠ACD=∠BAC,由折叠的性质可得∠BAC
=∠EAC,
∴∠ACD=∠EAC,∴AE=CE.
二、填空题
9.
【答案】
【解析】根据菱形的性质可知:应当旋转至少
10.
【答案】
11.
【答案】个
12.
【答案】.
【解析】∵四边形是矩形
∴
∵平分,所以
∴
∵
所以为等边三角形
∴所以
∴
13.
【答案】
【解析】如图,连结.
14.
【答案】4.8 【解析】∵S菱形=AC·BD=2AB·DH,∴AC·BD=2AB·DH.∵四边形ABCD是菱形,∴∠AOB=90°,AO=AC=4,BO=BD=3,∴在Rt△AOB中,AB==5,∴DH==4.8.
15.
【答案】
【解析】,所以可得面积为
16.
【答案】
【解析】,则,所以得到
三、解答题
17.
【答案】
∵四边形是平行四边形
∴,
∴
又∵
∴
又∵
显然
∴且
∴
∴四边形是平行四边形.
18.
【答案】
解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DFO=∠BEO.
又∵∠DOF=∠BOE,OD=OB,
∴△DOF≌△BOE(AAS),
∴DF=BE,
又∵DF∥BE,
∴四边形DEBF是平行四边形.
(2)∵DE=DF,四边形BEDF是平行四边形,
∴四边形BEDF是菱形,
∴DE=BE,EF⊥BD,OE=OF,
设AE=x,则DE=BE=8-x,
在Rt△ADE中,根据勾股定理,
得AE2+AD2=DE2,
∴x2+62=(8-x)2,
解得:x=,
∴DE=8-=.
在Rt△ABD中,根据勾股定理,
得AB2+AD2=BD2,
∴BD==10,
∴OD=BD=5,
在Rt△DOE中,根据勾股定理,得
DE2-OD2=OE2,
∴OE==,
∴EF=2OE=.
19.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,
由折叠性质可知,∠D=∠AD′E=60°,
∴∠AD′E=∠B=60°,
∴ED′∥BC,
又∵EC∥D′B,
∴四边形BCED′是平行四边形,(4分)
∴ED′=BC=AD=1,
∴DE=ED′=1,
又DC=AB=2,
∴EC=1,
∴EC=ED′,
∴四边形BCED′是菱形.(6分)
(2)
解图
解:如解图所示,由折叠性质PD′=PD,BD之长即为所求,(8分)
作DG⊥BA的延长线于点G,
∵∠DAB=120°,
∴∠DAG=60°,
∵∠G=90°,
∴∠ADG=30°,
在Rt△ADG中,AD=1,
∴AG=,DG=,(9分)
∵AB=2,
∴BG=,
在Rt△BDG中,由勾股定理得:BD2=BG2+DG2=7,
∴BD=,
即PD′+PB的最小值为.(10分)
20.
【答案】
解:(1)结论:DM⊥EM,DM=EM.
[解析]延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
(2)结论不变.DM⊥EM,DM=EM.
证明:延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
21.
【答案】
(1)解:
∵CF平分∠BCD,∴∠BCD=2∠BCF.
∵∠BCF=60°,∴∠BCD=2×60°=120°.
∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABC+∠BCD=180°.
∴∠ABC=180°-120°=60°.
(2)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∠BAD=∠DCB.
∴∠ABE=∠CDF.
∵AE,CF分别平分∠BAD和∠DCB,∴∠BAE=∠BAD=∠DCB=∠DCF.
在△ABE和△CDF中,∵∠ABE=∠CDF,AB=CD,∠BAE=∠DCF,
∴△ABE≌△CDF.
∴BE=DF.
22.
【答案】
,延长至,使,证明,测得
23.
【答案】
本题中存在两组“三垂直”,即图形与,与,从而可知,,,,从而,故≌,故,.又,从而.
24.
【答案】
如图所示,,分别过点、、作直线的垂线,、、为垂足;分别过、作的垂线,、为垂足.
显然,、、、、五点共圆,是直径.
由,,,且可知.
已知,,
则
故.
点评:类型的问题一般要转化为型的问题(当然,如果能够使用勾股定理、余弦定理等,大家也可以踊跃尝试),把握了这一点,就能及时调整思路,确保解题不会误入歧途.
八年级数学下册
第十八章
平行四边形
综合训练
一、选择题
1.
如图,若要使?ABCD成为菱形,则可添加的条件是
( )
A.AB=CD
B.AD=BC
C.AB=BC
D.AC=BD
2.
如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A.
7
B.
9
C.
10
D.
11
3.
(2020·抚顺本溪辽阳)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,AC=8,BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2
B.
C.3
D.4
4.
(2020·四川甘孜州)如图,菱形ABCD中,对角线AC,BD相交于点O,
E为AB的中点.若菱形ABCD的周长为32,则OE的长为(
)
A.3
B.4
C.5
D.6
5.
如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )
A.
B.
2
C.
+1
D.
2+1
6.
(3分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2
B.
C.3
D.4
7.
如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是
( )
A.矩形
B.菱形
C.一般的四边形
D.平行四边形
8.
如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
二、填空题
9.
在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是
10.
在矩形中,点为的中点,为上任意一点,交于点,交于点,当满足条件
时,四边形是矩形
11.
如图,在平行四边形中,与相交于点,图中共有
个平行四边形
12.
如图,矩形中,相交于点,平分交于,若,求=
13.
如图,已知、分别是正方形的边、上的点,、分别与对角线相交于、,若,则
.
14.
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.
15.
如图,有一矩形纸片,,将纸片折叠,使边落在边上,折痕为,在将以为折痕向右折叠,与交于点,则的面积为
16.
如图,是边长为的正方形,是内接于的正方形,,若则=
三、解答题
17.
如图,在平行四边形中,点、是对角线上的点,且,,求证:四边形是平行四边形.
18.
如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求EF的长.
19.
如图,?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P是直线l上的一个动点,请计算PD′+PB的最小值.
20.
如图,已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图①,点E在CD上,点G在BC的延长线上,判断DM,EM的数量关系与位置关系,请直接写出结论.
(2)如图②,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.
21.
(2020·重庆B卷)如图,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠DCB,交对角线BD于点E,F.
(1)若∠BCF=60°,求∠ABC的度数;
(2)求证:BE=DF.
22.
如图,点分别在正方形的边上,已知的周长等于正方形周长的一半,求的度数
23.
如图所示,在正方形中,、是内的两条射线,,,,,求证,.
24.
如图,是平行四边形较长的一条对角线,点是内部一点,于点,于点,于点,求证:.
人教版
八年级数学下册
第十八章
平行四边形
综合训练-答案
一、选择题
1.
【答案】C
2.
【答案】D 【解析】本题考查勾股定理、三角形的中位线定理和四边形的周长
.
解题思路:
?四边形EFGH的周长=EF+FG+HG+EH=11.
3.
【答案】B
【解析】根据菱形对角线互相垂直平分,求出菱形的边长,再结合等腰三角形的性质及判定得出OE=CE=DE,从而求出.∵四边形ABCD是菱形,∴OC=AC=4,
OD=BD=3,
AC⊥DB.∵OE=CE,∴∠EOC=OE∠DCO.∵∠DOE+∠EOC=∠ODC+∠ECO=90°,∴∠DOE=∠ODC,∴OE=DE,∴OE=DC.在Rt△DOC中,CD==5,∴OE=DC=.故选项B正确.
4.
【答案】B
【解析】本题考查了菱形的性质和直角三角形斜边上的中线性质.∵四边形ABCD是菱形,∴AB=BC=CD=DA.∵菱形ABCD的周长为32,∴AB=8.∵AC⊥BD,E为AB的中点,∴OE=AB=4.故选B.
5.
【答案】B 【解析】∵正方形ABCD的面积为1,∴BC=CD=1,∵E、F是边的中点,∴CE=CF=,∴EF==,则正方形EFGH的周长为4×=2.
6.
【答案】B
【解析】根据菱形的对角线互相垂直平分求出OB,OC,AC⊥BD,然后利用勾股定理列式求出BC,最后根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
∵菱形ABCD的对角线AC、BD相交于点O,
∴OBBD6=3,OA=OCAC8=4,AC⊥BD,
由勾股定理得,BC5,
∴AD=5,
∵OE=CE,
∴∠DCA=∠EOC,
∵四边形ABCD是菱形,
∴∠DCA=∠DAC,
∴∠DAC=∠EOC,
∴OE∥AD,
∵AO=OC,
∴OE是△ADC的中位线,
∴OEAD=2.5.
7.
【答案】B
8.
【答案】D 【解析】∵四边形ABCD为矩形,∴AB∥CD,∴∠ACD=∠BAC,由折叠的性质可得∠BAC
=∠EAC,
∴∠ACD=∠EAC,∴AE=CE.
二、填空题
9.
【答案】
【解析】根据菱形的性质可知:应当旋转至少
10.
【答案】
11.
【答案】个
12.
【答案】.
【解析】∵四边形是矩形
∴
∵平分,所以
∴
∵
所以为等边三角形
∴所以
∴
13.
【答案】
【解析】如图,连结.
14.
【答案】4.8 【解析】∵S菱形=AC·BD=2AB·DH,∴AC·BD=2AB·DH.∵四边形ABCD是菱形,∴∠AOB=90°,AO=AC=4,BO=BD=3,∴在Rt△AOB中,AB==5,∴DH==4.8.
15.
【答案】
【解析】,所以可得面积为
16.
【答案】
【解析】,则,所以得到
三、解答题
17.
【答案】
∵四边形是平行四边形
∴,
∴
又∵
∴
又∵
显然
∴且
∴
∴四边形是平行四边形.
18.
【答案】
解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DFO=∠BEO.
又∵∠DOF=∠BOE,OD=OB,
∴△DOF≌△BOE(AAS),
∴DF=BE,
又∵DF∥BE,
∴四边形DEBF是平行四边形.
(2)∵DE=DF,四边形BEDF是平行四边形,
∴四边形BEDF是菱形,
∴DE=BE,EF⊥BD,OE=OF,
设AE=x,则DE=BE=8-x,
在Rt△ADE中,根据勾股定理,
得AE2+AD2=DE2,
∴x2+62=(8-x)2,
解得:x=,
∴DE=8-=.
在Rt△ABD中,根据勾股定理,
得AB2+AD2=BD2,
∴BD==10,
∴OD=BD=5,
在Rt△DOE中,根据勾股定理,得
DE2-OD2=OE2,
∴OE==,
∴EF=2OE=.
19.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,
由折叠性质可知,∠D=∠AD′E=60°,
∴∠AD′E=∠B=60°,
∴ED′∥BC,
又∵EC∥D′B,
∴四边形BCED′是平行四边形,(4分)
∴ED′=BC=AD=1,
∴DE=ED′=1,
又DC=AB=2,
∴EC=1,
∴EC=ED′,
∴四边形BCED′是菱形.(6分)
(2)
解图
解:如解图所示,由折叠性质PD′=PD,BD之长即为所求,(8分)
作DG⊥BA的延长线于点G,
∵∠DAB=120°,
∴∠DAG=60°,
∵∠G=90°,
∴∠ADG=30°,
在Rt△ADG中,AD=1,
∴AG=,DG=,(9分)
∵AB=2,
∴BG=,
在Rt△BDG中,由勾股定理得:BD2=BG2+DG2=7,
∴BD=,
即PD′+PB的最小值为.(10分)
20.
【答案】
解:(1)结论:DM⊥EM,DM=EM.
[解析]延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
(2)结论不变.DM⊥EM,DM=EM.
证明:延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,
AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.
21.
【答案】
(1)解:
∵CF平分∠BCD,∴∠BCD=2∠BCF.
∵∠BCF=60°,∴∠BCD=2×60°=120°.
∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABC+∠BCD=180°.
∴∠ABC=180°-120°=60°.
(2)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∠BAD=∠DCB.
∴∠ABE=∠CDF.
∵AE,CF分别平分∠BAD和∠DCB,∴∠BAE=∠BAD=∠DCB=∠DCF.
在△ABE和△CDF中,∵∠ABE=∠CDF,AB=CD,∠BAE=∠DCF,
∴△ABE≌△CDF.
∴BE=DF.
22.
【答案】
,延长至,使,证明,测得
23.
【答案】
本题中存在两组“三垂直”,即图形与,与,从而可知,,,,从而,故≌,故,.又,从而.
24.
【答案】
如图所示,,分别过点、、作直线的垂线,、、为垂足;分别过、作的垂线,、为垂足.
显然,、、、、五点共圆,是直径.
由,,,且可知.
已知,,
则
故.
点评:类型的问题一般要转化为型的问题(当然,如果能够使用勾股定理、余弦定理等,大家也可以踊跃尝试),把握了这一点,就能及时调整思路,确保解题不会误入歧途.
