2020-2021学年人教版数学八年级下册:第十八章 平行四边形 解答题专题练习试卷(Word版含答案提升篇)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册:第十八章 平行四边形 解答题专题练习试卷(Word版含答案提升篇) |
|
|
| 格式 | docx | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 00:00:00 | ||
图片预览


文档简介
人教版数学八年级下册:第十八章
平行四边形
解答题专题练习(提升篇)
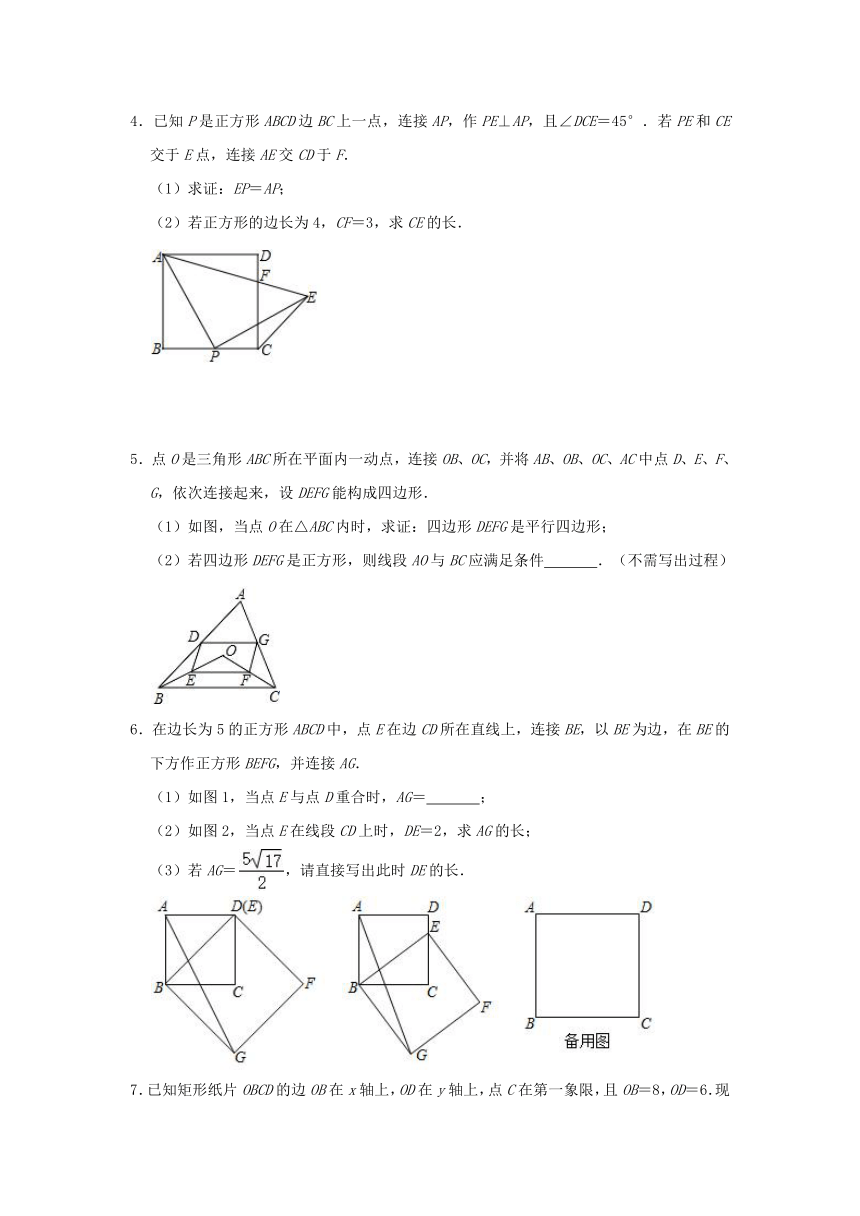
1.如图,在?ABCD中,点E是边CD的中点,连接BE并延长,交AD延长线于点F,连接BD、CF.
(1)求证:△CEB≌△DEF;
(2)若AB=BF,试判断四边形BCFD的形状,并证明.
2.已知,如图,在Rt△ABC中,E是两锐角平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.
3.如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
(1)求证:四边形ABCD是菱形;
(2)若∠EAF=60°,CF=2,求AF的长.
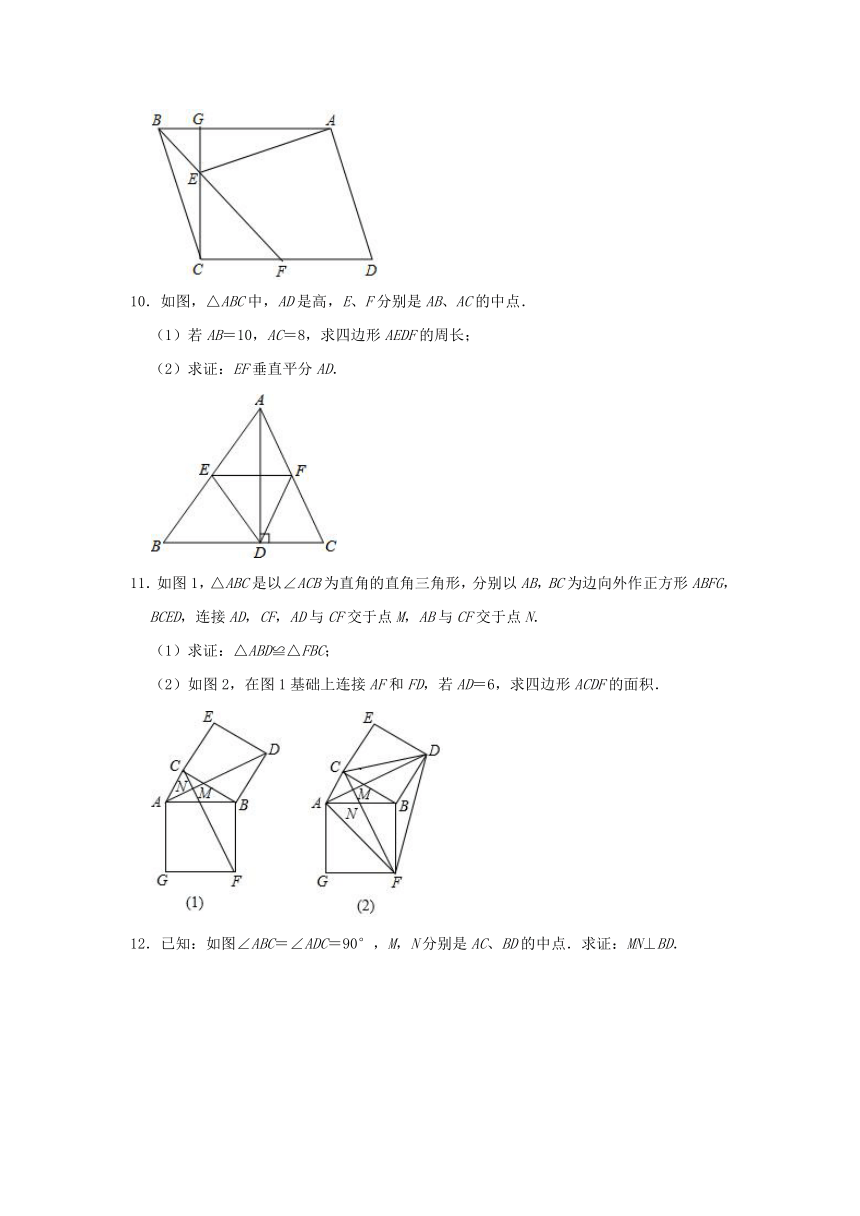
4.已知P是正方形ABCD边BC上一点,连接AP,作PE⊥AP,且∠DCE=45°.若PE和CE交于E点,连接AE交CD于F.
(1)求证:EP=AP;
(2)若正方形的边长为4,CF=3,求CE的长.
5.点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.
(1)如图,当点O在△ABC内时,求证:四边形DEFG是平行四边形;
(2)若四边形DEFG是正方形,则线段AO与BC应满足条件
.(不需写出过程)
6.在边长为5的正方形ABCD中,点E在边CD所在直线上,连接BE,以BE为边,在BE的下方作正方形BEFG,并连接AG.
(1)如图1,当点E与点D重合时,AG=
;
(2)如图2,当点E在线段CD上时,DE=2,求AG的长;
(3)若AG=,请直接写出此时DE的长.
7.已知矩形纸片OBCD的边OB在x轴上,OD在y轴上,点C在第一象限,且OB=8,OD=6.现将纸片折叠,折痕为EF
(点E、F是折痕与矩形的边的交点),点P为点D的对应点,再将纸片还原.
(Ⅰ)若点P落在矩形OBCD的边OB上,
①如图①,当点E与点O重合时,求点F的坐标;
②如图②,当点E在OB上,点F在DC上时,EF与DP交于点G,若OP=7,求点F的坐标;
(Ⅱ)若点P落在矩形OBCD的内部,且点E,F分别在边OD,边DC上,当OP取最小值时,求点P的坐标(直接写出结果即可).
8.如图,△ABC中,点O是边AC上一个动点(不与A、C重合),过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
(1)若CE=8,CF=6,求OC的长;
(2)当点O在边AC上运动到何处且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
9.如图,?ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CG于点E,连接AE,AE⊥AD.
(1)若BG=1,BC=,求EF的长度;
(2)求证:AB﹣BE=CF.
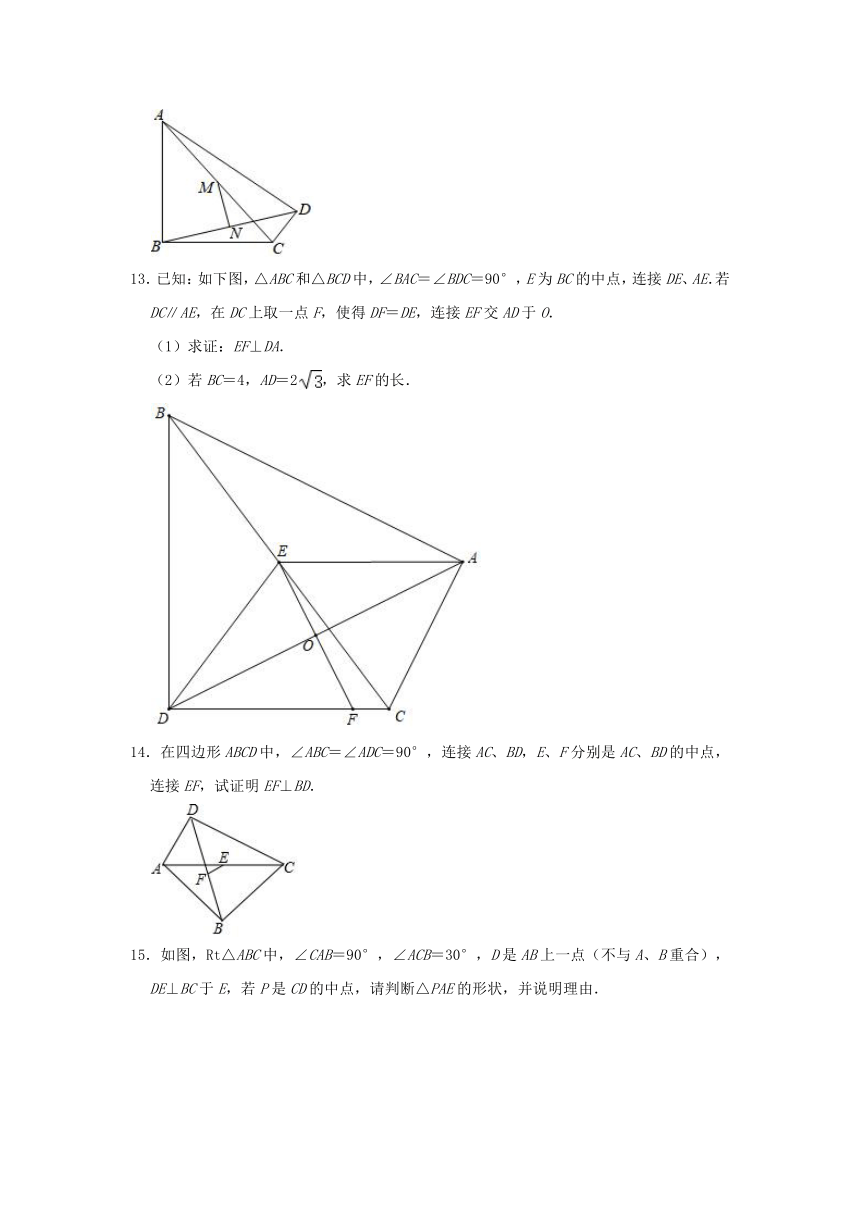
10.如图,△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
11.如图1,△ABC是以∠ACB为直角的直角三角形,分别以AB,BC为边向外作正方形ABFG,BCED,连接AD,CF,AD与CF交于点M,AB与CF交于点N.
(1)求证:△ABD≌△FBC;
(2)如图2,在图1基础上连接AF和FD,若AD=6,求四边形ACDF的面积.
12.已知:如图∠ABC=∠ADC=90°,M,N分别是AC、BD的中点.求证:MN⊥BD.
13.已知:如下图,△ABC和△BCD中,∠BAC=∠BDC=90°,E为BC的中点,连接DE、AE.若DC∥AE,在DC上取一点F,使得DF=DE,连接EF交AD于O.
(1)求证:EF⊥DA.
(2)若BC=4,AD=2,求EF的长.
14.在四边形ABCD中,∠ABC=∠ADC=90°,连接AC、BD,E、F分别是AC、BD的中点,连接EF,试证明EF⊥BD.
15.如图,Rt△ABC中,∠CAB=90°,∠ACB=30°,D是AB上一点(不与A、B重合),DE⊥BC于E,若P是CD的中点,请判断△PAE的形状,并说明理由.
参考答案
1.(1)证明:∵四边形ABCD是平行四边形
∴AF∥BC,
∴∠AFB=∠CBF,∠FDC=∠DCB,
∵点E是CD的中点,
∴BE=EF,
∴△CEB≌△DEF.
(2)解:结论:四边形BCFD是矩形,
理由:∵△CEB≌△DEF,
∴CE=DE,
∵BE=EF,
∴四边形BCFD是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵AB=BF,
∴BF=CD,
∴?BCFD为矩形.
2.证明:过E作EM⊥AB,
∵AE平分∠CAB,
∴EF=EM,
∵EB平分∠CBA,
∴EM=ED,
∴EF=ED,
∵ED⊥BC,EF⊥AC,△ABC是直角三角形,
∴∠CFE=∠CDE=∠C=90°,
∴四边形EFDC是矩形,
∵EF=ED,
∴四边形CDEF是正方形.
3.(1)证法一:连接AC,如图.
∵AE⊥BC,AF⊥DC,AE=AF,
∴∠ACF=∠ACE,
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAC=∠ACB.
∴∠DAC=∠DCA,
∴DA=DC,
∴四边形ABCD是菱形.
证法二:如图,
∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥DC,
∴∠AEB=∠AFD=90°,
又∵AE=AF,
∴△AEB≌△AFD.
∴AB=AD,
∴四边形ABCD是菱形.
(2)连接AC,如图.
∵AE⊥BC,AF⊥DC,∠EAF=60°,
∴∠ECF=120°,
∵四边形ABCD是菱形,
∴∠ACF=60°,
在Rt△CFA中,AF=CF?tan∠ACF=2.
4.(1)证明:连接AC,过P点作PG⊥BC交AC于G点,
∵四边形ABCD是正方形,
∴∠ACB=45°,∠BCD=90°,
∵PG⊥BC,
∴∠GPC=90°,
∴∠PGC=45°,
∴PG=PC,
∵∠DCE=45°,
∴∠AGP=∠ECP=90°+45°=135°,
∵AP⊥PE,
∴∠APE=∠GPC=90°,
∴∠APG=∠EPC=90°﹣∠GPE,
在△PAG和△PEC中
∴△PAG≌△PEC(ASA),
∴PE=PA;
(2)解:延长CB到Q,使BQ=DF,过E作EH⊥BC,EH交BC延长线于H,连接AQ,PF,
∵四边形ABCD是正方形,
∴∠D=∠DAB=∠ABC=90°,AD=AB,
∴∠ABQ=∠D=90°,
在△ABQ和△ADF中
∴△ABQ≌△ADF(SAS),
∴AQ=AF,∠DAF=∠QAB,
∵∠APE=90°,AP=PE,
∴∠PAE=∠AEP=45°,
∴∠AQP=∠QAB+∠BAP=∠DAF+∠BAP=∠DAB﹣∠PAE=90°﹣45°=45°=∠PAE,
在△QAP和△FAP中
∴△QAP≌△FAP(SAS),
∴QP=PE,
∵EH⊥BC,∠ABP=90°,∠APE=90°,
∴∠ABP=∠H=90°,∠APB=∠PEH=90°﹣∠EPH,
在△PEH和△APB中
∴△PEH≌△APB(AAS),
∴BP=EH,
∵∠H=90°,∠DCE=45°,
∴∠ECH=45°=∠CEH,
∴CH=EH=BP,
设EH=CH=BP=x,
∴PC=4﹣x,PF=BQ+BP=DF+BP=4﹣3+x=1+x,
在Rt△PCF中,由勾股定理得:(1+x)2=(4﹣x)2+32,
解之得:x=,
即CH=EH=,
∴在Rt△CHE中,由勾股定理得:CE=CH=.
5.(1)证明:∵AB、OB、OC、AC的中点分别为D、E、F、G,
∴DG∥BC,DG=BC,EF∥BC,EF=BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:∵D、E分别是AB、OB的中点,
∴DE∥OA,DE=OA,
∵四边形DEFG是正方形,
∴DE⊥EF,DE=EF,
∴AO与BC垂直且相等.
故答案为:垂直且相等.
6.解:(1)如图1,连接CG,
∵四边形ABCD和四边形EBGF是正方形,
∴∠CDB=∠CBD=45°,∠DBG=90°,BD=BG,
∴∠CBG=45°,
∴∠CBG=∠CBD,
∵BC=BC,
∴△CBD≌△CBG(SAS),
∴∠DCB=∠BCG=90°,DC=CG=5,
∴G,C,D三点共线,
∴AG===5;
故答案为:5;
(2)如图2,过点G作GK⊥AB,交AB的延长线于K,
∵DE=2,DC=5,
∴CE=3,
∵∠EBG=∠EBC+∠CBG=90°,∠CBG+∠GBK=90°,
∴∠EBC=∠GBK,
∵BE=BG,∠K=∠BCE=90°,
∴△BCE≌△BKG(AAS),
∴CE=KG=3,BC=BK=5,
∴AK=10,
由勾股定理得:AG==;
(3)分三种情况:
①当点E在CD的延长线上时,如图3,同理知△BCE≌△BKG(AAS),
∴BC=BK=5,
∵AG=,
由勾股定理得:KG==,
∴CE=KG=,此种情况不成立;
②当点E在边CD上时,如图4,
同理得:DE=;
③当点E在DC的延长线上时,如图5,
同理得CE=GK=,
∴DE=5+=,
综上,DE的长是或.
7.解:(Ⅰ)①∵折痕为EF,点P为点D的对应点,
∴△DOF≌△POF.
∴∠DOF=∠POF=45°.
∵四边形OBCD是矩形,
∴∠ODF=90°.
∴∠DFO=∠DOF=45°.
∴DF=DO=6.
∴点F的坐标为(6,6);
②∵折痕为EF,点P为点D的对应点,
∴DG=PG,EF⊥PD.
∵四边形OBCD是矩形,
∴DC∥OB,
∴∠FDG=∠EPG.
∵∠DGF=∠PGE,
∴△DGF≌△PGE(ASA).
∴DF=PE.
∵DF∥PE,
∴四边形DEPF是平行四边形.
∵EF⊥PD,
∴?DEPF是菱形,
设菱形的边长为x,则DE=EP=x.
∵OP=7,
∴OE=7﹣x,
在Rt△ODE中,由勾股定理得OD2+OE2=DE2.
∴62+(7﹣x)2=x2,
解得.
∴,
∴点F的坐标为(,6);
(Ⅱ)P(,).
8.解:(1)∵OF是∠BCA的外角平分线,
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠FCD,
∴∠OFC=∠OCF,
∴OF=OC,
∴OE=OF;
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
∴∠ECF=90°,
∵CE=8,CF=6,
∴EF==10,
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∴CO是△ECF上的中线,
∴CO=EF=5;
(2)点O是AC的中点且∠ACB=90°,
理由:∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴四边形AECF为平行四边形;
∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,
∴∠2+∠5=90°,即∠ECF=90°,
∴?AECF为矩形,
又∵AC⊥EF.
∴?AECF是正方形.
∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
9.解:(1)∵CG⊥AB,BG=1,,
∴.
∵∠ABF=45°,
∴△BGE是等腰直角三角形,
∴EG=BG=1,
∴EC=CG﹣EG=3﹣1=2,
∵在平行四边形ABCD中,AB∥CD,∠ABF=45°,CG⊥AB,
∴∠CFE=∠ABF=45°,∠FCE=∠BGE=90°,
∴△ECF是等腰直角三角形,
∴EF==2;
(2)证明:过E作EH⊥BE交AB于H,
∵∠ABF=45°,∠BEH=90°,
∴△BEH是等腰直角三角形,
∴,BE=HE,
∴∠BHE=45°,
∴∠AHE=180°﹣∠BHE=180°﹣45°=135°,
由(1)知,△BGE和△ECF都是等腰直角三角形,
∴∠BEG=45°,CE=CF,
∴∠BEC=180°﹣∠BEG=180°﹣45°=135°,
∴∠AHE=∠CEB,
∵AE⊥AD,
∴∠DAE=90°,
∴∠BAD=∠DAE+∠EAB=90°+∠EAB,
由(1)知,∠FCE=90°,
∴∠BCD=∠FCE+∠BCG=90°+∠BCG,
∵在平行四边形ABCD中,∠BAD=∠BCD,
∴90°+∠EAB=90°+∠BCG,
∴∠EAB=∠BCG,
即∠EAH=∠BCE,
在△△EAH和△BCE中,
∴△EAH≌△BCE(AAS),
∴AH=CE=CF,
∴AB﹣BE=AB﹣BH=AH=CF,
即AB﹣BE=CF.
10.(1)解:∵AD是高,E、F分别是AB、AC的中点,
∴DE=AE=AB=×10=5,DF=AF=AC=×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)证明:∵DE=AE,DF=AF,
∴EF垂直平分AD.
11.(1)证明:∵四边形ABFG和四边形BCED是正方形,
∴BC=BD,AB=BF,∠CBD=∠ABF=90°,
∴∠CBD+∠ABC=∠ABF+∠ABC,
∴∠ABD=∠CBF,
在△ABD和△FBC中
,
∴△ABD≌△FBC(SAS);
(2)解:∵△ABD≌△FBC,
∴∠BAD=∠BFC,AD=FC=6,
∴∠AMF=180°﹣(∠BAD+∠ANM)
=180°﹣(∠BFC+∠BNM)
=180°﹣(180°﹣∠ABF)
=180°﹣(180°﹣90°)
=90°,
即AD⊥CF,
∴四边形ACDF的面积S=S△ACD+S△ADF
=+
=
=
=18.
12.证明:如图,连接BM、DM,
∵∠ABC=∠ADC=90°,M是AC的中点,
∴BM=DM=AC,
∵点N是BD的中点,
∴MN⊥BD.
13.解:(1)∵△ABC和△BCD中,∠BAC=∠BDC=90°,E为BC的中点,
∴DE=AE=BC,
∴∠EDA=∠EAD,
∵DC∥AE,
∴∠ADC=∠EAD,
∴∠ADC=∠EDA,
∵DF=DE,
∴EF⊥DA;
(2)∵BC=4,
∴DE=BC=2,
∵DE=AE,,
∴DO=AD=,
在Rt△DEO中,EO==1,
∵DF=DE,
∴EF=2EO=2.
14.证明:如图,连接BE、DE,
∵∠ABC=∠ADC=90°,E是AC的中点,
∴BE=DE=AC,
∵F是BD的中点,
∴EF⊥BD.
15.解:△PAE的形状为等边三角形;理由如下:
∵在Rt△CAD中,∠CAD=90°,P是斜边CD的中点,
∴PA=PC=CD,
∴∠ACD=∠PAC,
∴∠APD=∠ACD+∠PAC=2∠ACD,
同理:在Rt△CED中,PE=PC=CD,∠DPE=2∠DCB,
∴PA=PE,即△PAE是等腰三角形,
∴∠APE=2∠ACB=2×30°=60°,
∴△PAE是等边三角形.
平行四边形
解答题专题练习(提升篇)
1.如图,在?ABCD中,点E是边CD的中点,连接BE并延长,交AD延长线于点F,连接BD、CF.
(1)求证:△CEB≌△DEF;
(2)若AB=BF,试判断四边形BCFD的形状,并证明.
2.已知,如图,在Rt△ABC中,E是两锐角平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.
3.如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
(1)求证:四边形ABCD是菱形;
(2)若∠EAF=60°,CF=2,求AF的长.
4.已知P是正方形ABCD边BC上一点,连接AP,作PE⊥AP,且∠DCE=45°.若PE和CE交于E点,连接AE交CD于F.
(1)求证:EP=AP;
(2)若正方形的边长为4,CF=3,求CE的长.
5.点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.
(1)如图,当点O在△ABC内时,求证:四边形DEFG是平行四边形;
(2)若四边形DEFG是正方形,则线段AO与BC应满足条件
.(不需写出过程)
6.在边长为5的正方形ABCD中,点E在边CD所在直线上,连接BE,以BE为边,在BE的下方作正方形BEFG,并连接AG.
(1)如图1,当点E与点D重合时,AG=
;
(2)如图2,当点E在线段CD上时,DE=2,求AG的长;
(3)若AG=,请直接写出此时DE的长.
7.已知矩形纸片OBCD的边OB在x轴上,OD在y轴上,点C在第一象限,且OB=8,OD=6.现将纸片折叠,折痕为EF
(点E、F是折痕与矩形的边的交点),点P为点D的对应点,再将纸片还原.
(Ⅰ)若点P落在矩形OBCD的边OB上,
①如图①,当点E与点O重合时,求点F的坐标;
②如图②,当点E在OB上,点F在DC上时,EF与DP交于点G,若OP=7,求点F的坐标;
(Ⅱ)若点P落在矩形OBCD的内部,且点E,F分别在边OD,边DC上,当OP取最小值时,求点P的坐标(直接写出结果即可).
8.如图,△ABC中,点O是边AC上一个动点(不与A、C重合),过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
(1)若CE=8,CF=6,求OC的长;
(2)当点O在边AC上运动到何处且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
9.如图,?ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CG于点E,连接AE,AE⊥AD.
(1)若BG=1,BC=,求EF的长度;
(2)求证:AB﹣BE=CF.
10.如图,△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
11.如图1,△ABC是以∠ACB为直角的直角三角形,分别以AB,BC为边向外作正方形ABFG,BCED,连接AD,CF,AD与CF交于点M,AB与CF交于点N.
(1)求证:△ABD≌△FBC;
(2)如图2,在图1基础上连接AF和FD,若AD=6,求四边形ACDF的面积.
12.已知:如图∠ABC=∠ADC=90°,M,N分别是AC、BD的中点.求证:MN⊥BD.
13.已知:如下图,△ABC和△BCD中,∠BAC=∠BDC=90°,E为BC的中点,连接DE、AE.若DC∥AE,在DC上取一点F,使得DF=DE,连接EF交AD于O.
(1)求证:EF⊥DA.
(2)若BC=4,AD=2,求EF的长.
14.在四边形ABCD中,∠ABC=∠ADC=90°,连接AC、BD,E、F分别是AC、BD的中点,连接EF,试证明EF⊥BD.
15.如图,Rt△ABC中,∠CAB=90°,∠ACB=30°,D是AB上一点(不与A、B重合),DE⊥BC于E,若P是CD的中点,请判断△PAE的形状,并说明理由.
参考答案
1.(1)证明:∵四边形ABCD是平行四边形
∴AF∥BC,
∴∠AFB=∠CBF,∠FDC=∠DCB,
∵点E是CD的中点,
∴BE=EF,
∴△CEB≌△DEF.
(2)解:结论:四边形BCFD是矩形,
理由:∵△CEB≌△DEF,
∴CE=DE,
∵BE=EF,
∴四边形BCFD是平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵AB=BF,
∴BF=CD,
∴?BCFD为矩形.
2.证明:过E作EM⊥AB,
∵AE平分∠CAB,
∴EF=EM,
∵EB平分∠CBA,
∴EM=ED,
∴EF=ED,
∵ED⊥BC,EF⊥AC,△ABC是直角三角形,
∴∠CFE=∠CDE=∠C=90°,
∴四边形EFDC是矩形,
∵EF=ED,
∴四边形CDEF是正方形.
3.(1)证法一:连接AC,如图.
∵AE⊥BC,AF⊥DC,AE=AF,
∴∠ACF=∠ACE,
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAC=∠ACB.
∴∠DAC=∠DCA,
∴DA=DC,
∴四边形ABCD是菱形.
证法二:如图,
∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥DC,
∴∠AEB=∠AFD=90°,
又∵AE=AF,
∴△AEB≌△AFD.
∴AB=AD,
∴四边形ABCD是菱形.
(2)连接AC,如图.
∵AE⊥BC,AF⊥DC,∠EAF=60°,
∴∠ECF=120°,
∵四边形ABCD是菱形,
∴∠ACF=60°,
在Rt△CFA中,AF=CF?tan∠ACF=2.
4.(1)证明:连接AC,过P点作PG⊥BC交AC于G点,
∵四边形ABCD是正方形,
∴∠ACB=45°,∠BCD=90°,
∵PG⊥BC,
∴∠GPC=90°,
∴∠PGC=45°,
∴PG=PC,
∵∠DCE=45°,
∴∠AGP=∠ECP=90°+45°=135°,
∵AP⊥PE,
∴∠APE=∠GPC=90°,
∴∠APG=∠EPC=90°﹣∠GPE,
在△PAG和△PEC中
∴△PAG≌△PEC(ASA),
∴PE=PA;
(2)解:延长CB到Q,使BQ=DF,过E作EH⊥BC,EH交BC延长线于H,连接AQ,PF,
∵四边形ABCD是正方形,
∴∠D=∠DAB=∠ABC=90°,AD=AB,
∴∠ABQ=∠D=90°,
在△ABQ和△ADF中
∴△ABQ≌△ADF(SAS),
∴AQ=AF,∠DAF=∠QAB,
∵∠APE=90°,AP=PE,
∴∠PAE=∠AEP=45°,
∴∠AQP=∠QAB+∠BAP=∠DAF+∠BAP=∠DAB﹣∠PAE=90°﹣45°=45°=∠PAE,
在△QAP和△FAP中
∴△QAP≌△FAP(SAS),
∴QP=PE,
∵EH⊥BC,∠ABP=90°,∠APE=90°,
∴∠ABP=∠H=90°,∠APB=∠PEH=90°﹣∠EPH,
在△PEH和△APB中
∴△PEH≌△APB(AAS),
∴BP=EH,
∵∠H=90°,∠DCE=45°,
∴∠ECH=45°=∠CEH,
∴CH=EH=BP,
设EH=CH=BP=x,
∴PC=4﹣x,PF=BQ+BP=DF+BP=4﹣3+x=1+x,
在Rt△PCF中,由勾股定理得:(1+x)2=(4﹣x)2+32,
解之得:x=,
即CH=EH=,
∴在Rt△CHE中,由勾股定理得:CE=CH=.
5.(1)证明:∵AB、OB、OC、AC的中点分别为D、E、F、G,
∴DG∥BC,DG=BC,EF∥BC,EF=BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:∵D、E分别是AB、OB的中点,
∴DE∥OA,DE=OA,
∵四边形DEFG是正方形,
∴DE⊥EF,DE=EF,
∴AO与BC垂直且相等.
故答案为:垂直且相等.
6.解:(1)如图1,连接CG,
∵四边形ABCD和四边形EBGF是正方形,
∴∠CDB=∠CBD=45°,∠DBG=90°,BD=BG,
∴∠CBG=45°,
∴∠CBG=∠CBD,
∵BC=BC,
∴△CBD≌△CBG(SAS),
∴∠DCB=∠BCG=90°,DC=CG=5,
∴G,C,D三点共线,
∴AG===5;
故答案为:5;
(2)如图2,过点G作GK⊥AB,交AB的延长线于K,
∵DE=2,DC=5,
∴CE=3,
∵∠EBG=∠EBC+∠CBG=90°,∠CBG+∠GBK=90°,
∴∠EBC=∠GBK,
∵BE=BG,∠K=∠BCE=90°,
∴△BCE≌△BKG(AAS),
∴CE=KG=3,BC=BK=5,
∴AK=10,
由勾股定理得:AG==;
(3)分三种情况:
①当点E在CD的延长线上时,如图3,同理知△BCE≌△BKG(AAS),
∴BC=BK=5,
∵AG=,
由勾股定理得:KG==,
∴CE=KG=,此种情况不成立;
②当点E在边CD上时,如图4,
同理得:DE=;
③当点E在DC的延长线上时,如图5,
同理得CE=GK=,
∴DE=5+=,
综上,DE的长是或.
7.解:(Ⅰ)①∵折痕为EF,点P为点D的对应点,
∴△DOF≌△POF.
∴∠DOF=∠POF=45°.
∵四边形OBCD是矩形,
∴∠ODF=90°.
∴∠DFO=∠DOF=45°.
∴DF=DO=6.
∴点F的坐标为(6,6);
②∵折痕为EF,点P为点D的对应点,
∴DG=PG,EF⊥PD.
∵四边形OBCD是矩形,
∴DC∥OB,
∴∠FDG=∠EPG.
∵∠DGF=∠PGE,
∴△DGF≌△PGE(ASA).
∴DF=PE.
∵DF∥PE,
∴四边形DEPF是平行四边形.
∵EF⊥PD,
∴?DEPF是菱形,
设菱形的边长为x,则DE=EP=x.
∵OP=7,
∴OE=7﹣x,
在Rt△ODE中,由勾股定理得OD2+OE2=DE2.
∴62+(7﹣x)2=x2,
解得.
∴,
∴点F的坐标为(,6);
(Ⅱ)P(,).
8.解:(1)∵OF是∠BCA的外角平分线,
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠FCD,
∴∠OFC=∠OCF,
∴OF=OC,
∴OE=OF;
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
∴∠ECF=90°,
∵CE=8,CF=6,
∴EF==10,
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∴CO是△ECF上的中线,
∴CO=EF=5;
(2)点O是AC的中点且∠ACB=90°,
理由:∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴四边形AECF为平行四边形;
∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,
∴∠2+∠5=90°,即∠ECF=90°,
∴?AECF为矩形,
又∵AC⊥EF.
∴?AECF是正方形.
∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
9.解:(1)∵CG⊥AB,BG=1,,
∴.
∵∠ABF=45°,
∴△BGE是等腰直角三角形,
∴EG=BG=1,
∴EC=CG﹣EG=3﹣1=2,
∵在平行四边形ABCD中,AB∥CD,∠ABF=45°,CG⊥AB,
∴∠CFE=∠ABF=45°,∠FCE=∠BGE=90°,
∴△ECF是等腰直角三角形,
∴EF==2;
(2)证明:过E作EH⊥BE交AB于H,
∵∠ABF=45°,∠BEH=90°,
∴△BEH是等腰直角三角形,
∴,BE=HE,
∴∠BHE=45°,
∴∠AHE=180°﹣∠BHE=180°﹣45°=135°,
由(1)知,△BGE和△ECF都是等腰直角三角形,
∴∠BEG=45°,CE=CF,
∴∠BEC=180°﹣∠BEG=180°﹣45°=135°,
∴∠AHE=∠CEB,
∵AE⊥AD,
∴∠DAE=90°,
∴∠BAD=∠DAE+∠EAB=90°+∠EAB,
由(1)知,∠FCE=90°,
∴∠BCD=∠FCE+∠BCG=90°+∠BCG,
∵在平行四边形ABCD中,∠BAD=∠BCD,
∴90°+∠EAB=90°+∠BCG,
∴∠EAB=∠BCG,
即∠EAH=∠BCE,
在△△EAH和△BCE中,
∴△EAH≌△BCE(AAS),
∴AH=CE=CF,
∴AB﹣BE=AB﹣BH=AH=CF,
即AB﹣BE=CF.
10.(1)解:∵AD是高,E、F分别是AB、AC的中点,
∴DE=AE=AB=×10=5,DF=AF=AC=×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)证明:∵DE=AE,DF=AF,
∴EF垂直平分AD.
11.(1)证明:∵四边形ABFG和四边形BCED是正方形,
∴BC=BD,AB=BF,∠CBD=∠ABF=90°,
∴∠CBD+∠ABC=∠ABF+∠ABC,
∴∠ABD=∠CBF,
在△ABD和△FBC中
,
∴△ABD≌△FBC(SAS);
(2)解:∵△ABD≌△FBC,
∴∠BAD=∠BFC,AD=FC=6,
∴∠AMF=180°﹣(∠BAD+∠ANM)
=180°﹣(∠BFC+∠BNM)
=180°﹣(180°﹣∠ABF)
=180°﹣(180°﹣90°)
=90°,
即AD⊥CF,
∴四边形ACDF的面积S=S△ACD+S△ADF
=+
=
=
=18.
12.证明:如图,连接BM、DM,
∵∠ABC=∠ADC=90°,M是AC的中点,
∴BM=DM=AC,
∵点N是BD的中点,
∴MN⊥BD.
13.解:(1)∵△ABC和△BCD中,∠BAC=∠BDC=90°,E为BC的中点,
∴DE=AE=BC,
∴∠EDA=∠EAD,
∵DC∥AE,
∴∠ADC=∠EAD,
∴∠ADC=∠EDA,
∵DF=DE,
∴EF⊥DA;
(2)∵BC=4,
∴DE=BC=2,
∵DE=AE,,
∴DO=AD=,
在Rt△DEO中,EO==1,
∵DF=DE,
∴EF=2EO=2.
14.证明:如图,连接BE、DE,
∵∠ABC=∠ADC=90°,E是AC的中点,
∴BE=DE=AC,
∵F是BD的中点,
∴EF⊥BD.
15.解:△PAE的形状为等边三角形;理由如下:
∵在Rt△CAD中,∠CAD=90°,P是斜边CD的中点,
∴PA=PC=CD,
∴∠ACD=∠PAC,
∴∠APD=∠ACD+∠PAC=2∠ACD,
同理:在Rt△CED中,PE=PC=CD,∠DPE=2∠DCB,
∴PA=PE,即△PAE是等腰三角形,
∴∠APE=2∠ACB=2×30°=60°,
∴△PAE是等边三角形.
