2020-2021学年高一下学期数学人教A版必修5第一章1.1.1 正弦定理 课件(共19张PPT)
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版必修5第一章1.1.1 正弦定理 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 614.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
1.1.1正弦定理
一、情景导入:
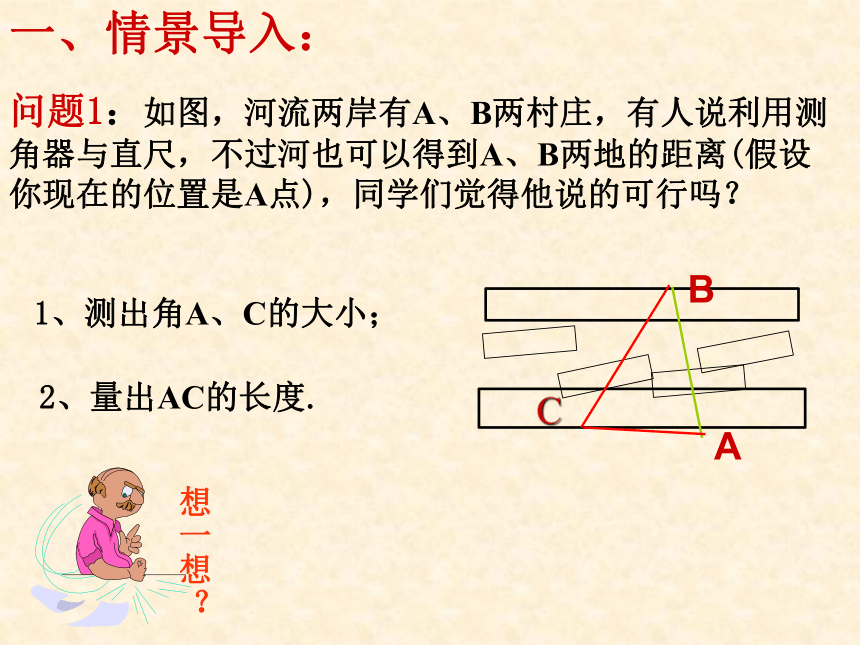
问题1:如图,河流两岸有A、B两村庄,有人说利用测角器与直尺,不过河也可以得到A、B两地的距离(假设你现在的位置是A点),同学们觉得他说的可行吗?
A
B
C
1、测出角A、C的大小;
2、量出AC的长度.
想一想?
A
B
C
a
b
c
问题2:在Rt三角形中,角C=90o,如何定义
sinA,
sinB?
算一算
求c边;
求角B大小.
在右图直角三角形中,
(1)若已知角
(2)若已知
求c边;
对于一般的三角形,还有什么常用的定理和结论?
(1)三个内角和为180o;
(3)大边对大角,小边对小角.
(2)两边之和大于第三边,两边之差小于第三边;
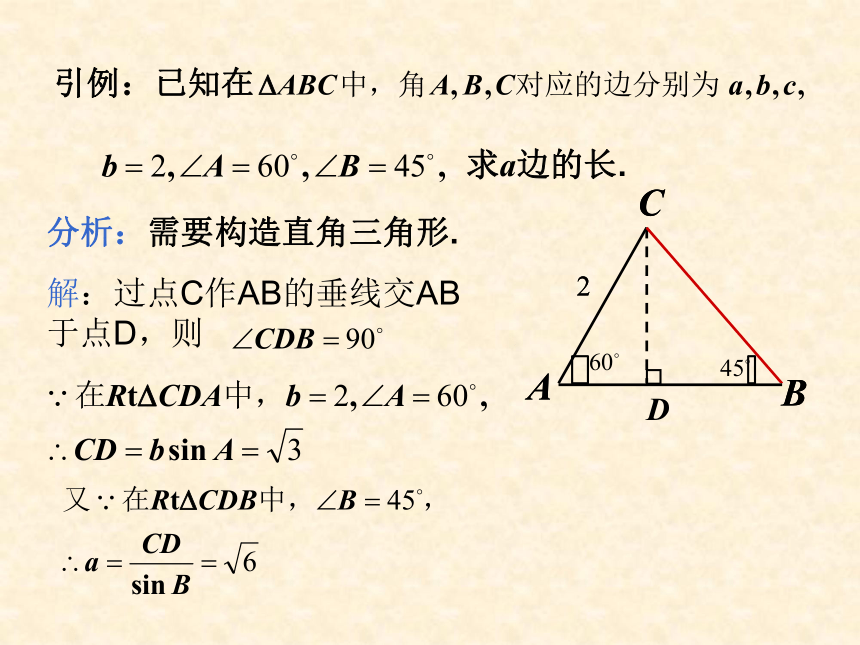
引例:已知在
求a边的长.
分析:需要构造直角三角形.
解:过点C作AB的垂线交AB于点D,则
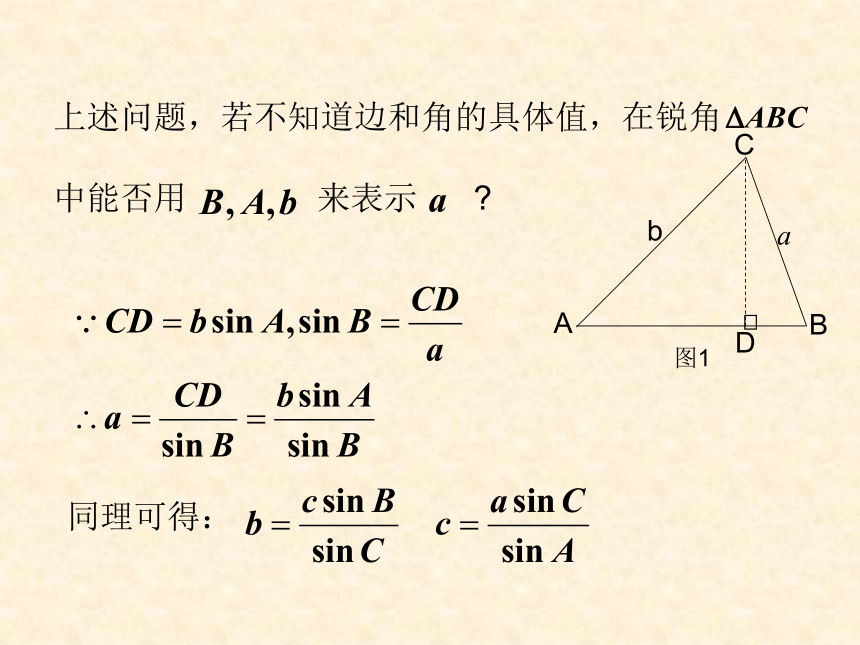
上述问题,若不知道边和角的具体值,在锐角
中能否用
来表示
?
C
b
a
B
A
图1
D
同理可得:
整理可得:
即
若是钝角三角形呢,是否也有以上等式成立?直角呢?
当△ABC是钝角三角形时,设边AB上的高是CD,根据三角函数的定义,
同理,做BC边上的高可得
CD=asinB=bsinA,则
所以,
A
B
C
D
a
c
b
E
即:
在一个三角形中,各边和它所对角的正弦的比相等,
即
正弦定理
一般地,把三角形的三个角和它们的对边叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形
课
动
互
堂
探
究
类型一
已知两角及一边解三角形
[例1]在△ABC
中,已知
求c边大小。
[分析]已知两角和一边,可由内角和求第三个角C,再由正弦定理求边.
解:
根据三角形内角和定理,
(1)在△ABC中,已知
A=30°,B=120°,b=12。
解三角形.
练习:
类型二
已知两边及其中一边的对角解三角形
[例2]在△ABC
中,已知
求角C大小.
[分析]已知两边和其中一边的对角,可由正弦定理求出另外一边的对角的正弦值,再根据角的范围来确定角C大小.
解:
(大边对大角)
变式1
已知a=16,
b=
,
A=30°解三角形.
所以B=60°,
或B=120°
C=90°
C=30°
当B=120°时
当
时
B=60°
解:由正弦定理得
变式2
已知a=2,
b=
6
,
A=30°求角B.
解:由正弦定理得
1.在解三角形中,什么时候有一个解,什么时候有两个解,什么时候无解?
思考
2.试证明
(2R为三角形外接圆的直径)
正弦定理用途:
解斜三角形
已知两角和任一边,求其它两边和一角;
已知两边及其中一边对角,求另一边的对角及其他的边和角。
实现三角形当中边角之间的转化
1.1.1正弦定理
一、情景导入:
问题1:如图,河流两岸有A、B两村庄,有人说利用测角器与直尺,不过河也可以得到A、B两地的距离(假设你现在的位置是A点),同学们觉得他说的可行吗?
A
B
C
1、测出角A、C的大小;
2、量出AC的长度.
想一想?
A
B
C
a
b
c
问题2:在Rt三角形中,角C=90o,如何定义
sinA,
sinB?
算一算
求c边;
求角B大小.
在右图直角三角形中,
(1)若已知角
(2)若已知
求c边;
对于一般的三角形,还有什么常用的定理和结论?
(1)三个内角和为180o;
(3)大边对大角,小边对小角.
(2)两边之和大于第三边,两边之差小于第三边;
引例:已知在
求a边的长.
分析:需要构造直角三角形.
解:过点C作AB的垂线交AB于点D,则
上述问题,若不知道边和角的具体值,在锐角
中能否用
来表示
?
C
b
a
B
A
图1
D
同理可得:
整理可得:
即
若是钝角三角形呢,是否也有以上等式成立?直角呢?
当△ABC是钝角三角形时,设边AB上的高是CD,根据三角函数的定义,
同理,做BC边上的高可得
CD=asinB=bsinA,则
所以,
A
B
C
D
a
c
b
E
即:
在一个三角形中,各边和它所对角的正弦的比相等,
即
正弦定理
一般地,把三角形的三个角和它们的对边叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形
课
动
互
堂
探
究
类型一
已知两角及一边解三角形
[例1]在△ABC
中,已知
求c边大小。
[分析]已知两角和一边,可由内角和求第三个角C,再由正弦定理求边.
解:
根据三角形内角和定理,
(1)在△ABC中,已知
A=30°,B=120°,b=12。
解三角形.
练习:
类型二
已知两边及其中一边的对角解三角形
[例2]在△ABC
中,已知
求角C大小.
[分析]已知两边和其中一边的对角,可由正弦定理求出另外一边的对角的正弦值,再根据角的范围来确定角C大小.
解:
(大边对大角)
变式1
已知a=16,
b=
,
A=30°解三角形.
所以B=60°,
或B=120°
C=90°
C=30°
当B=120°时
当
时
B=60°
解:由正弦定理得
变式2
已知a=2,
b=
6
,
A=30°求角B.
解:由正弦定理得
1.在解三角形中,什么时候有一个解,什么时候有两个解,什么时候无解?
思考
2.试证明
(2R为三角形外接圆的直径)
正弦定理用途:
解斜三角形
已知两角和任一边,求其它两边和一角;
已知两边及其中一边对角,求另一边的对角及其他的边和角。
实现三角形当中边角之间的转化
