2020-2021学年九年级下册数学北师大新版《第3章 圆》单元测试题(word版含解析)
文档属性
| 名称 | 2020-2021学年九年级下册数学北师大新版《第3章 圆》单元测试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 441.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 14:22:59 | ||
图片预览



文档简介
2020-2021学年九年级下册数学北师大新版《第3章
圆》单元测试题
一.选择题
1.下列命题中,正确的个数是( )
(1)直径是弦,但弦不一定是直径;(2)半圆是弧,但弧不一定是半圆;
(3)半径相等的两个圆是等圆;(4)一条弦把圆分成的两段弧中,至少有一段是优弧.
A.1个
B.2个
C.3个
D.4个
2.如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
A.40°
B.130°
C.120°
D.150°
3.一个点到一个圆的最短距离是3cm,最长距离是6cm,则这个圆的半径是( )
A.4.5cm
B.1.5cm
C.4.5cm或1.5cm
D.9cm或3cm
4.如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是( )
A.相离
B.相交
C.相切
D.不确定
5.如图,有一块边长为6
cm的正三角形ABC木块,点P是边CA延长线上的一点,在A,P之间拉一细绳,绳长AP为15
cm.握住点P,拉直细绳,把它紧紧缠绕在三角形ABC木块上(缠绕时木块不动),则点P运动的路线长为(精确到0.1厘米,π≈3.14)( )
A.28.3cm
B.28.2cm
C.56.5cm
D.56.6cm
6.正方形的边长是4cm,那么它的外接圆半径为( )
A.
cm
B.
cm
C.2cm
D.4cm
7.如图,PA=PB,OE⊥PA,OF⊥PB,则以下结论:①OP是∠APB的平分线;②PE=PF③CA=BD;④CD∥AB;其中正确的有( )个.
A.4
B.3
C.2
D.1
8.如图,△ABC内接于⊙O,AH⊥BC于点H.若AC=24,AH=18,⊙O的半径OC=13,则AB的长为( )
A.15
B.
C.13
D.
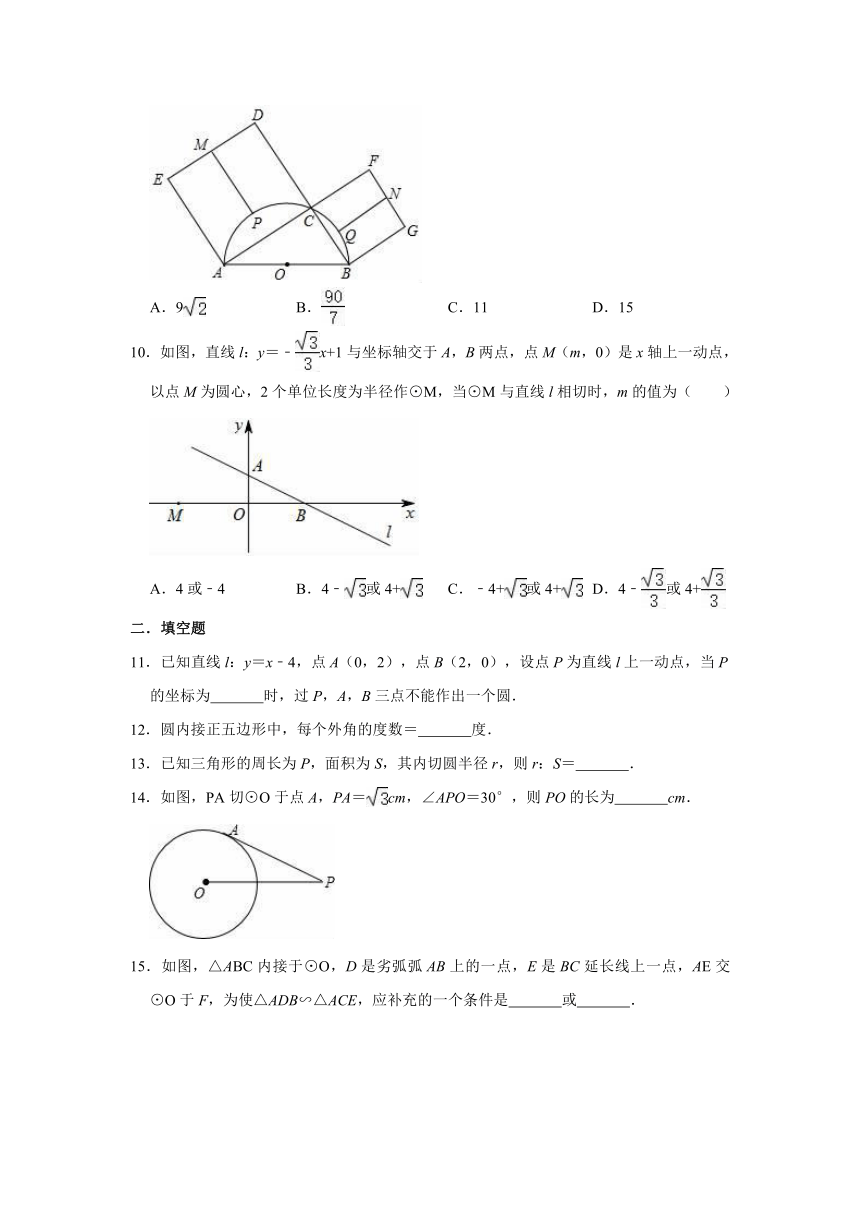
9.如图,C是以AB为直径的半圆O上一点,连接AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,,的中点分别是M、N、P、Q,若MP+NQ=12,AC+BC=18,则AB的长为( )
A.9
B.
C.11
D.15
10.如图,直线l:y=﹣x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线l相切时,m的值为( )
A.4或﹣4
B.4﹣或4+
C.﹣4+或4+
D.4﹣或4+
二.填空题
11.已知直线l:y=x﹣4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为
时,过P,A,B三点不能作出一个圆.
12.圆内接正五边形中,每个外角的度数=
度.
13.已知三角形的周长为P,面积为S,其内切圆半径r,则r:S=
.
14.如图,PA切⊙O于点A,PA=cm,∠APO=30°,则PO的长为
cm.
15.如图,△ABC内接于⊙O,D是劣弧弧AB上的一点,E是BC延长线上一点,AE交⊙O于F,为使△ADB∽△ACE,应补充的一个条件是
或
.
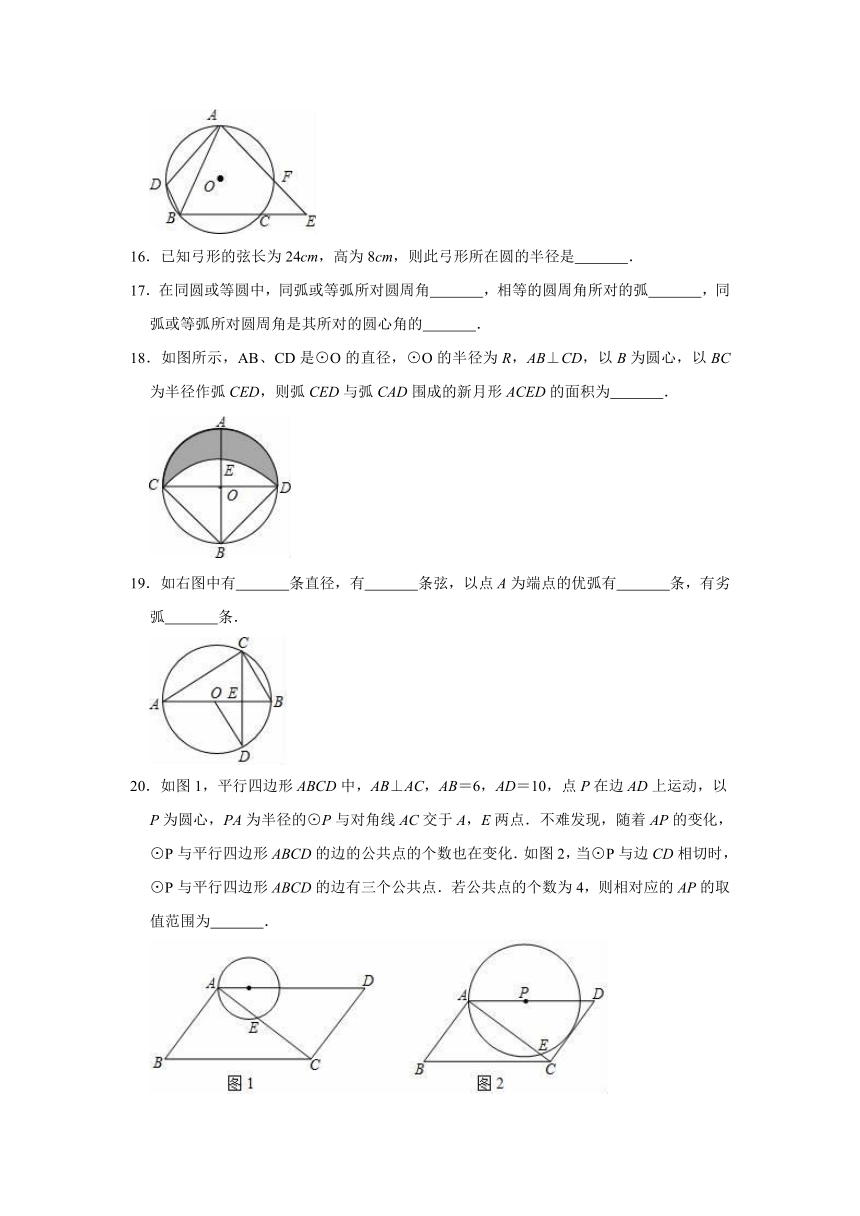
16.已知弓形的弦长为24cm,高为8cm,则此弓形所在圆的半径是
.
17.在同圆或等圆中,同弧或等弧所对圆周角
,相等的圆周角所对的弧
,同弧或等弧所对圆周角是其所对的圆心角的
.
18.如图所示,AB、CD是⊙O的直径,⊙O的半径为R,AB⊥CD,以B为圆心,以BC为半径作弧CED,则弧CED与弧CAD围成的新月形ACED的面积为
.
19.如右图中有
条直径,有
条弦,以点A为端点的优弧有
条,有劣弧
条.
20.如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为
.
三.解答题
21.如图,在图中,用图形(阴影)表示与A的距离小于或等于2cm的所有点组成的图形.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当BC=CE=2时,求DE的长度.
23.如图,半径为2的正三角形ABC的中心为O,过O与两个顶点画弧,求这三条弧所围成的阴影部分的面积.
24.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
25.如图,有一拱桥为圆弧形,跨度AB=60米,拱高PM=18米,当洪水泛滥时,跨度只有30米时要采取紧急措施,测量人员测得水面A1B1到拱顶距离只有4米时,是否采取紧急措施?
26.如图所示,△ABC中,AC=BC,以AC为直径的⊙O交AB于E,作△BCA的外角平分线CF交⊙O于F,连接EF,求证:EF=BC.
27.如图,AB是⊙O的直径,延长AB到C,使BC=,切线BF分别交切线CD及AD的延长线于E、F,求∠F的度数.
28.已知,如图,正六边形ABCDEF的边长为6cm,求这个正六边形的外接圆半径R、边心距r6、面积S6.
参考答案与试题解析
一.选择题
1.解:当弦为直径时,不会把圆分成一段优弧一段劣弧,
∴(4)为假命题
而(1)、(2)、(3)均正确
故选:C.
2.解:∵圆内接四边形ABCD中,∠B=50°,
∴∠D=180°﹣50°=130°.
故选:B.
3.解:如图,分点在圆内与圆外两种情况.
①当点P在⊙O内时,
此时PA=3cm,PB=6cm,AB=9cm,
因此半径为4.5cm;
②当点P在⊙O外时,如图此时PA=3cm,PB=6cm,
直线PB过圆心O,直径AB=6﹣3=3cm,
因此半径为1.5cm.
故选:C.
4.解:过C作CD⊥AB,垂足为D,
∵∠C=90°,∠A=60°,
∴∠B=30°,
∵BC=4cm,
∴CD=2cm,
∵2<3,
∴⊙C与直线AB相交.
故选:B.
5.解:第一个小扇形的弧长等于cm,
第二个为cm,
第三个为三者相加得56.5cm.
故选:C.
6.解:如图,连接OA,OD,
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴△AOD是等腰直角三角形,
∴OA2+OD2=AD2,即2OA2=42,解得OA=2(cm).
故选:B.
7.解:
连接OP、OC、OA、OD、OB、CD、AB.
∵PC?PA=PD?PB(相交弦定理),PA=PB(已知),
∴PC=PD,
∴AC=BD;
在△AOC和△BOD中,
∵∠AOC=∠BOD(等弦对等角),
OA=OB(半径),
OD=OC(半径),
∴△AOC≌△BOD,
∴③CA=BD;
OE=OF;
又∵OE⊥PA,OF⊥PB,
∴①OP是∠APB的平分线;
∴②PE=PF;
在△PCD和△PAB中,
PC:PA=PD:PB,
∠DPC=∠BPA,
∴△PCD∽△PAB,
∴∠PDC=PBA,
∴④CD∥AB;
综上所述,①②③④均正确,故答案选A.
8.解:如图,作直径AE,连接CE,
∴∠ACE=90°,
∵AH⊥BC,
∴∠AHB=90°,
∴∠ACE=∠AHB,
∵∠E=∠B,
∴△ACE∽△AHB,
∴=,
∴AB=,
∵AC=24,AH=18,AE=2OC=26,
∴AB==.
则AB的长为.
故选:B.
9.解:连接OP,OQ,
∵DE,FG,,的中点分别是M,N,P,Q,
∴OP⊥AC,OQ⊥BC,
∴H、I是AC、BD的中点,
∴OH+OI=(AC+BC)=9,
∵MH+NI=AC+BC=18,MP+NQ=12,
∴PH+QI=18﹣12=6,
∴AB=OP+OQ=OH+OI+PH+QI=9+6=15,
故选:D.
10.解:在y=﹣x+1中,
令x=0,则y=1,
令y=0,则x=,
∴A(0,1),B(,0),
∴AB=2;
如图,设⊙M与AB相切与C,
连接MC,则MC=2,MC⊥AB,
∵∠MCB=∠AOB=90°,∠ABO=∠CBM,
∴△BMC~△BAO,
∴=,即=,
∴BM=4,
∴OM=4﹣,或OM=4+.
∴m=﹣4,m=4+.
故选:C.
二.填空题
11.解:设直线AB的解析式为y=kx+b,
∵A(0,2),点B(2,0),
∴,
解得,
∴y=﹣x+2.
解方程组,得,
∴当P的坐标为(3,﹣1)时,过P,A,B三点不能作出一个圆.
故答案为(3,﹣1).
12.解:360°÷5=72°.
故答案为:72.
13.解:∵⊙O是△ABC的内切圆,
∴OD⊥AC,OE⊥AB,OF⊥BC,OD=OE=OF=r,
∴S△ABC=S△AOB+S△BOC+S△AOC=AB?OE+OC?AB+OF?BC=r(AB+AC+BC)=Pr,
∴r:S=2:P.
14.解:连接OA,得到∠OAP=90°.
已知PA=cm,∠APO=30°,则PO==2(cm).
15.解:∵四边形ADBC是⊙O的内接四边形,
∴∠ACE=∠D,∴当∠BAD=∠EAC或∠ABD=∠E时,△ADB∽△ACE.
16.解:如右图所示,
CD=24,AB=8,
设OB=OC=xcm,
∵OB⊥CD,
∴AC=CD=12,∠OAC=90°,
在Rt△OAC中,OC2=OA2+AC2,
∴x2=(x﹣8)2+122,
解得x=13,
答:弓形所在圆的半径是13cm.
故答案是13cm.
17.解:由圆心角、弧、弦的关系及圆周角定理可知:在同圆或等圆中,同弧或等弧所对圆周角
相等,
相等的圆周角所对的弧
相等,
同弧或等弧所对圆周角是其所对的圆心角的一半.
故答案为:相等、相等、一半.
18.解:∵DC为直径,
∴∠CBD=90°,
∵AB⊥CD,
∴∠COB=90°,
∴BC=BD===R,
∴弧CED与弧CAD围成的新月形ACED的面积S=S△CBD+S圆O﹣S扇形CBD=R×R+R2﹣=R2,
故答案为:R2.
19.解:图中直径只有AB这1条,弦有AC、AB、CD、BC这4条,以点A为端点的优弧有、这2条,劣弧有、这2条,
故答案为:1、4、2、2.
20.解:∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
当⊙P与BC相切时,设切点为G,如图3,
S?ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
三.解答题
21.
解:如图,与A的距离小于或等于2cm的所有点组成的图形是如图所示的阴影部分.
22.(1)证明:∵OD⊥AC,
∴=,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD⊥AC,
∴AE=CE=2,
在Rt△ABC中,AB==2,
∴OD=,
∵AE=CE,OA=OB,
∴OE为△ABC的中位线,
∴OE=BC=1,
∴DE=﹣1.
23.解:作△ABC的外接圆,连接AO并延长交⊙O于A′、同理得到BB′、CC′;
∵△ABC是正三角形,
∴△OAB′也是正三角形;
∴S弓形OA=S扇形AB′O﹣S△AB′O=﹣2××=;
所以S阴影=6×()=4π﹣6.
24.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
25.解:连接OA、OA1,如下图所示:
由题可得:AB=60m,PM=18m,PN=4m,OA=OA1=OP=R
OP⊥AB,OP⊥A1B1
由垂径定理可得:AM=MB=30m
在Rt△AMO中,由勾股定理可得:
AO2=AM2+MO2
即R2=302+(R﹣18)2
解得R=34m
∵PN=4m,OP=R=34m
∴ON=30m
在Rt△ONA1中,由勾股定理可得:
A1N2=A1O2﹣ON2
可得A1N=16m
故A1B1=32m>30m
故不用采取紧急措施.
26.证明:∵CA=CB,
∴∠B=∠A,
又∵∠DCA=2∠FCA,∠DCA=∠A+∠B=2∠A,
∴∠FCA=∠A.
∴CF∥AB.
又∵∠FCA=∠FEA(同弧所对的圆周角相等),
∴∠FEA=∠B.
∴BC∥EF.
∴四边形CFEB为平行四边形.
∴EF=BC.
27.解:连接OD,如图,
∵CD切⊙O于D,
∴OD⊥DC,
又∵BC=,
∴OC=2OD,
∴∠C=30°,∠DOC=60°,
而OD=OA,
∴∠A=30°,
又∵BF为⊙O的切线,
∴BF⊥AB,
∴∠F=90°﹣∠A=60°.
28.解:连接OA,OB,过点O作OG⊥AB于G,
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=6,即R=6,
∵OA=OB=6,OG⊥AB,
∴AG=AB=×6=3,
∴在Rt△AOG中,r6=OG==3cm,
∴S6=×6×6×3=54cm2.
圆》单元测试题
一.选择题
1.下列命题中,正确的个数是( )
(1)直径是弦,但弦不一定是直径;(2)半圆是弧,但弧不一定是半圆;
(3)半径相等的两个圆是等圆;(4)一条弦把圆分成的两段弧中,至少有一段是优弧.
A.1个
B.2个
C.3个
D.4个
2.如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
A.40°
B.130°
C.120°
D.150°
3.一个点到一个圆的最短距离是3cm,最长距离是6cm,则这个圆的半径是( )
A.4.5cm
B.1.5cm
C.4.5cm或1.5cm
D.9cm或3cm
4.如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是( )
A.相离
B.相交
C.相切
D.不确定
5.如图,有一块边长为6
cm的正三角形ABC木块,点P是边CA延长线上的一点,在A,P之间拉一细绳,绳长AP为15
cm.握住点P,拉直细绳,把它紧紧缠绕在三角形ABC木块上(缠绕时木块不动),则点P运动的路线长为(精确到0.1厘米,π≈3.14)( )
A.28.3cm
B.28.2cm
C.56.5cm
D.56.6cm
6.正方形的边长是4cm,那么它的外接圆半径为( )
A.
cm
B.
cm
C.2cm
D.4cm
7.如图,PA=PB,OE⊥PA,OF⊥PB,则以下结论:①OP是∠APB的平分线;②PE=PF③CA=BD;④CD∥AB;其中正确的有( )个.
A.4
B.3
C.2
D.1
8.如图,△ABC内接于⊙O,AH⊥BC于点H.若AC=24,AH=18,⊙O的半径OC=13,则AB的长为( )
A.15
B.
C.13
D.
9.如图,C是以AB为直径的半圆O上一点,连接AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,,的中点分别是M、N、P、Q,若MP+NQ=12,AC+BC=18,则AB的长为( )
A.9
B.
C.11
D.15
10.如图,直线l:y=﹣x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线l相切时,m的值为( )
A.4或﹣4
B.4﹣或4+
C.﹣4+或4+
D.4﹣或4+
二.填空题
11.已知直线l:y=x﹣4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为
时,过P,A,B三点不能作出一个圆.
12.圆内接正五边形中,每个外角的度数=
度.
13.已知三角形的周长为P,面积为S,其内切圆半径r,则r:S=
.
14.如图,PA切⊙O于点A,PA=cm,∠APO=30°,则PO的长为
cm.
15.如图,△ABC内接于⊙O,D是劣弧弧AB上的一点,E是BC延长线上一点,AE交⊙O于F,为使△ADB∽△ACE,应补充的一个条件是
或
.
16.已知弓形的弦长为24cm,高为8cm,则此弓形所在圆的半径是
.
17.在同圆或等圆中,同弧或等弧所对圆周角
,相等的圆周角所对的弧
,同弧或等弧所对圆周角是其所对的圆心角的
.
18.如图所示,AB、CD是⊙O的直径,⊙O的半径为R,AB⊥CD,以B为圆心,以BC为半径作弧CED,则弧CED与弧CAD围成的新月形ACED的面积为
.
19.如右图中有
条直径,有
条弦,以点A为端点的优弧有
条,有劣弧
条.
20.如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.不难发现,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化.如图2,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点.若公共点的个数为4,则相对应的AP的取值范围为
.
三.解答题
21.如图,在图中,用图形(阴影)表示与A的距离小于或等于2cm的所有点组成的图形.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当BC=CE=2时,求DE的长度.
23.如图,半径为2的正三角形ABC的中心为O,过O与两个顶点画弧,求这三条弧所围成的阴影部分的面积.
24.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
25.如图,有一拱桥为圆弧形,跨度AB=60米,拱高PM=18米,当洪水泛滥时,跨度只有30米时要采取紧急措施,测量人员测得水面A1B1到拱顶距离只有4米时,是否采取紧急措施?
26.如图所示,△ABC中,AC=BC,以AC为直径的⊙O交AB于E,作△BCA的外角平分线CF交⊙O于F,连接EF,求证:EF=BC.
27.如图,AB是⊙O的直径,延长AB到C,使BC=,切线BF分别交切线CD及AD的延长线于E、F,求∠F的度数.
28.已知,如图,正六边形ABCDEF的边长为6cm,求这个正六边形的外接圆半径R、边心距r6、面积S6.
参考答案与试题解析
一.选择题
1.解:当弦为直径时,不会把圆分成一段优弧一段劣弧,
∴(4)为假命题
而(1)、(2)、(3)均正确
故选:C.
2.解:∵圆内接四边形ABCD中,∠B=50°,
∴∠D=180°﹣50°=130°.
故选:B.
3.解:如图,分点在圆内与圆外两种情况.
①当点P在⊙O内时,
此时PA=3cm,PB=6cm,AB=9cm,
因此半径为4.5cm;
②当点P在⊙O外时,如图此时PA=3cm,PB=6cm,
直线PB过圆心O,直径AB=6﹣3=3cm,
因此半径为1.5cm.
故选:C.
4.解:过C作CD⊥AB,垂足为D,
∵∠C=90°,∠A=60°,
∴∠B=30°,
∵BC=4cm,
∴CD=2cm,
∵2<3,
∴⊙C与直线AB相交.
故选:B.
5.解:第一个小扇形的弧长等于cm,
第二个为cm,
第三个为三者相加得56.5cm.
故选:C.
6.解:如图,连接OA,OD,
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴△AOD是等腰直角三角形,
∴OA2+OD2=AD2,即2OA2=42,解得OA=2(cm).
故选:B.
7.解:
连接OP、OC、OA、OD、OB、CD、AB.
∵PC?PA=PD?PB(相交弦定理),PA=PB(已知),
∴PC=PD,
∴AC=BD;
在△AOC和△BOD中,
∵∠AOC=∠BOD(等弦对等角),
OA=OB(半径),
OD=OC(半径),
∴△AOC≌△BOD,
∴③CA=BD;
OE=OF;
又∵OE⊥PA,OF⊥PB,
∴①OP是∠APB的平分线;
∴②PE=PF;
在△PCD和△PAB中,
PC:PA=PD:PB,
∠DPC=∠BPA,
∴△PCD∽△PAB,
∴∠PDC=PBA,
∴④CD∥AB;
综上所述,①②③④均正确,故答案选A.
8.解:如图,作直径AE,连接CE,
∴∠ACE=90°,
∵AH⊥BC,
∴∠AHB=90°,
∴∠ACE=∠AHB,
∵∠E=∠B,
∴△ACE∽△AHB,
∴=,
∴AB=,
∵AC=24,AH=18,AE=2OC=26,
∴AB==.
则AB的长为.
故选:B.
9.解:连接OP,OQ,
∵DE,FG,,的中点分别是M,N,P,Q,
∴OP⊥AC,OQ⊥BC,
∴H、I是AC、BD的中点,
∴OH+OI=(AC+BC)=9,
∵MH+NI=AC+BC=18,MP+NQ=12,
∴PH+QI=18﹣12=6,
∴AB=OP+OQ=OH+OI+PH+QI=9+6=15,
故选:D.
10.解:在y=﹣x+1中,
令x=0,则y=1,
令y=0,则x=,
∴A(0,1),B(,0),
∴AB=2;
如图,设⊙M与AB相切与C,
连接MC,则MC=2,MC⊥AB,
∵∠MCB=∠AOB=90°,∠ABO=∠CBM,
∴△BMC~△BAO,
∴=,即=,
∴BM=4,
∴OM=4﹣,或OM=4+.
∴m=﹣4,m=4+.
故选:C.
二.填空题
11.解:设直线AB的解析式为y=kx+b,
∵A(0,2),点B(2,0),
∴,
解得,
∴y=﹣x+2.
解方程组,得,
∴当P的坐标为(3,﹣1)时,过P,A,B三点不能作出一个圆.
故答案为(3,﹣1).
12.解:360°÷5=72°.
故答案为:72.
13.解:∵⊙O是△ABC的内切圆,
∴OD⊥AC,OE⊥AB,OF⊥BC,OD=OE=OF=r,
∴S△ABC=S△AOB+S△BOC+S△AOC=AB?OE+OC?AB+OF?BC=r(AB+AC+BC)=Pr,
∴r:S=2:P.
14.解:连接OA,得到∠OAP=90°.
已知PA=cm,∠APO=30°,则PO==2(cm).
15.解:∵四边形ADBC是⊙O的内接四边形,
∴∠ACE=∠D,∴当∠BAD=∠EAC或∠ABD=∠E时,△ADB∽△ACE.
16.解:如右图所示,
CD=24,AB=8,
设OB=OC=xcm,
∵OB⊥CD,
∴AC=CD=12,∠OAC=90°,
在Rt△OAC中,OC2=OA2+AC2,
∴x2=(x﹣8)2+122,
解得x=13,
答:弓形所在圆的半径是13cm.
故答案是13cm.
17.解:由圆心角、弧、弦的关系及圆周角定理可知:在同圆或等圆中,同弧或等弧所对圆周角
相等,
相等的圆周角所对的弧
相等,
同弧或等弧所对圆周角是其所对的圆心角的一半.
故答案为:相等、相等、一半.
18.解:∵DC为直径,
∴∠CBD=90°,
∵AB⊥CD,
∴∠COB=90°,
∴BC=BD===R,
∴弧CED与弧CAD围成的新月形ACED的面积S=S△CBD+S圆O﹣S扇形CBD=R×R+R2﹣=R2,
故答案为:R2.
19.解:图中直径只有AB这1条,弦有AC、AB、CD、BC这4条,以点A为端点的优弧有、这2条,劣弧有、这2条,
故答案为:1、4、2、2.
20.解:∵平行四边形ABCD中,AB=6,AD=10,
∴BC=AD=10,
∵AB⊥AC,
∴在Rt△ABC中,由勾股定理得:AC===8,
如图2所示,连接PF,
设AP=x,则DP=10﹣x,PF=x,
∵⊙P与边CD相切于点F,
∴PF⊥CD,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴AC⊥CD,
∴AC∥PF,
∴△DPF∽△DAC,
∴=,
∴=,
∴x=,
即AP=;
当⊙P与BC相切时,设切点为G,如图3,
S?ABCD=×6×8×2=10PG,
∴PG=,
①当⊙P与边AD、CD分别有两个公共点时,<AP<,即此时⊙P与平行四边形ABCD的边的公共点的个数为4;
②⊙P过点A、C、D三点,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=5,
综上所述,AP的值的取值范围是:<AP<或AP=5,
故答案为:<AP<或AP=5.
三.解答题
21.
解:如图,与A的距离小于或等于2cm的所有点组成的图形是如图所示的阴影部分.
22.(1)证明:∵OD⊥AC,
∴=,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD⊥AC,
∴AE=CE=2,
在Rt△ABC中,AB==2,
∴OD=,
∵AE=CE,OA=OB,
∴OE为△ABC的中位线,
∴OE=BC=1,
∴DE=﹣1.
23.解:作△ABC的外接圆,连接AO并延长交⊙O于A′、同理得到BB′、CC′;
∵△ABC是正三角形,
∴△OAB′也是正三角形;
∴S弓形OA=S扇形AB′O﹣S△AB′O=﹣2××=;
所以S阴影=6×()=4π﹣6.
24.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
25.解:连接OA、OA1,如下图所示:
由题可得:AB=60m,PM=18m,PN=4m,OA=OA1=OP=R
OP⊥AB,OP⊥A1B1
由垂径定理可得:AM=MB=30m
在Rt△AMO中,由勾股定理可得:
AO2=AM2+MO2
即R2=302+(R﹣18)2
解得R=34m
∵PN=4m,OP=R=34m
∴ON=30m
在Rt△ONA1中,由勾股定理可得:
A1N2=A1O2﹣ON2
可得A1N=16m
故A1B1=32m>30m
故不用采取紧急措施.
26.证明:∵CA=CB,
∴∠B=∠A,
又∵∠DCA=2∠FCA,∠DCA=∠A+∠B=2∠A,
∴∠FCA=∠A.
∴CF∥AB.
又∵∠FCA=∠FEA(同弧所对的圆周角相等),
∴∠FEA=∠B.
∴BC∥EF.
∴四边形CFEB为平行四边形.
∴EF=BC.
27.解:连接OD,如图,
∵CD切⊙O于D,
∴OD⊥DC,
又∵BC=,
∴OC=2OD,
∴∠C=30°,∠DOC=60°,
而OD=OA,
∴∠A=30°,
又∵BF为⊙O的切线,
∴BF⊥AB,
∴∠F=90°﹣∠A=60°.
28.解:连接OA,OB,过点O作OG⊥AB于G,
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴OA=OB=6,即R=6,
∵OA=OB=6,OG⊥AB,
∴AG=AB=×6=3,
∴在Rt△AOG中,r6=OG==3cm,
∴S6=×6×6×3=54cm2.
