2020-2021学年高一下学期数学人教A版必修5第一章1.1.2 余弦定理 课件(共20张PPT)
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版必修5第一章1.1.2 余弦定理 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 891.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 21:59:59 | ||
图片预览







文档简介
(共20张PPT)
余弦定理
一、复习回顾
1、回顾正弦定理以及正弦定理能解决的解三角形
问题的类型。
?
(1)已知两个角和一条边
(2)已知两条边和一边的对角
正弦定理:
正弦定理能解决的问题类型:
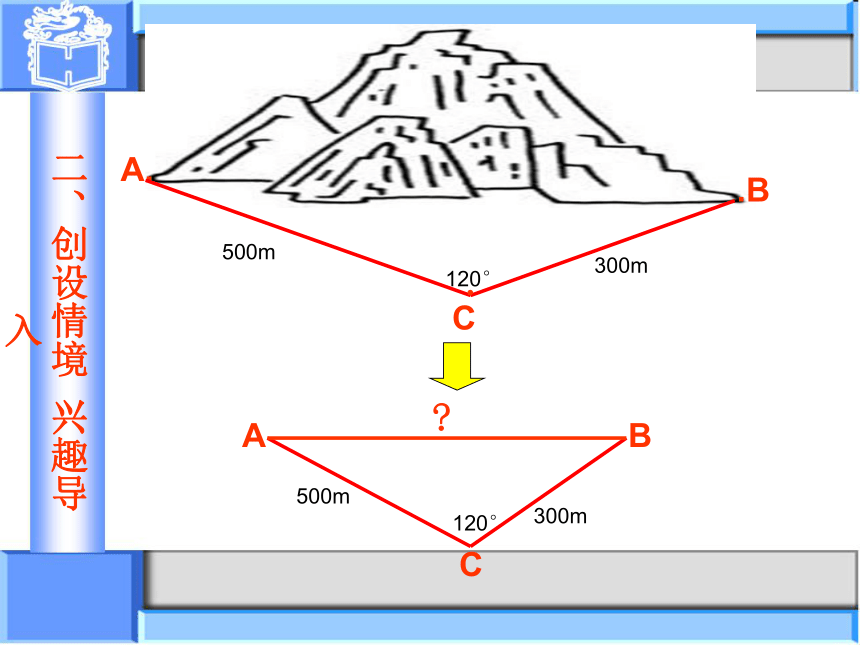
二、创设情境
兴趣导入
A·
·
B
A.
.B
120°
500m
300m
A
B
C
120°
500m
300m
?
C
.
二、创设情境
兴趣导入
二、创设情境
兴趣导入
1、如何用初中的三角方法来求AB的长
2、如何边、角为一般的结论是否成立
如图,
三、向量法证明余弦定理
由向量的减法,
A
B
C
?
自
主
探
究
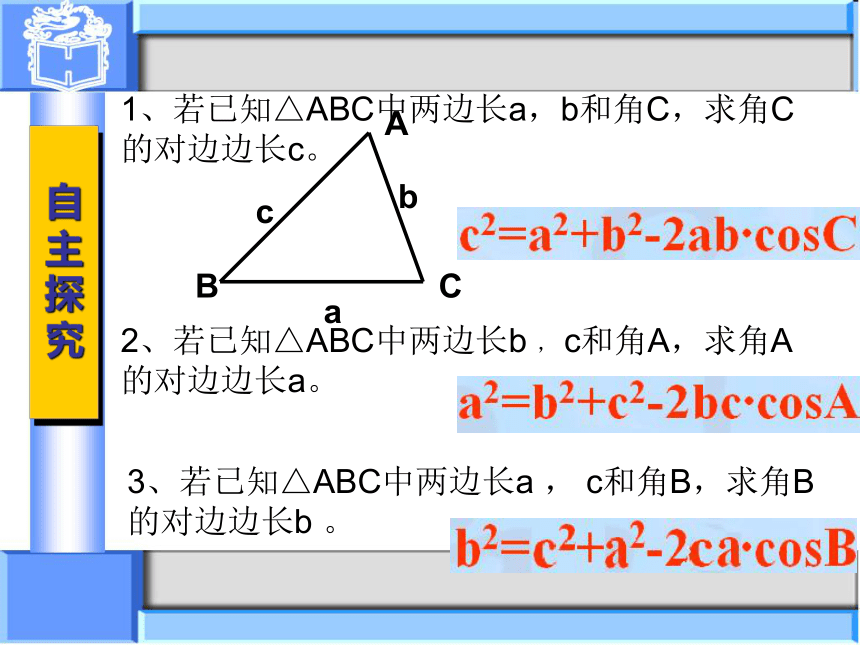
1、若已知△ABC中两边长a,b和角C,求角C的对边边长c。
2、若已知△ABC中两边长b
,
c和角A,求角A的对边边长a。
A
C
B
a
c
b
3、若已知△ABC中两边长a
,
c和角B,求角B的对边边长b
。
余弦定理:三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。
a
=b
+c-2bccosA
b
=c
+a-2cacosB
c
=a
+b-2abcosC
2
2
2
2
2
2
2
2
2
应用余弦定理,我们就可以从已知的两边和夹角计算出三角形的第三条边。
知三求一
从余弦定理,可以得到它的推论
四、余弦定理的推论
B
ac
c
a
b
cos
2
2
2
2
-
+
=
思考
如果已知三角形的三边,如何确定三个角?
余弦定理的推论:
四、余弦定理的推论
应用余弦定理的推论,我们就可以从三角形的三边计算出三角形的三个角。
勾股定理指出了直角三角形中三边平方之间的关系,余弦定理则指出了一般三角形中三边平方之间的关系,如何看这两个定理之间的关系?
C为锐角
余弦定理可以看作是勾股定理的推广,勾股定理是余弦定理的特例
cosC>0
C为直角
cosC=0
cosC<0
C为钝角
五、巩固知识
典型例题
例1:在三角形ABC中,C=120°,b=500,a=300,求c及sinA,sinB
情景题
A
B
C
?
500
300
120°
例2:在△ABC中,已知a=2,
,
,求A。
C
B
A
a=2
例3:在△ABC中,已知a=2,
,
,解三角形。
C
B
A
a=2
练习2:在△ABC中,已知b=3,
,
B=30°,解三角形
六、巩固知识
随堂练习
练习1:在△ABC中,c=3,A=45°,B=75°,求a
练习3:在△ABC中,已知a=5,b=7,c=8,则△ABC(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
思考
在解三角形的过程中,求某一个角有时既可以用余弦定理,也可以用正弦定理,两种方法有什么利弊呢?
(2)用余弦定理推论,解唯一,可以免去判断取舍。
(1)用正弦定理,计算相对简单,但解不唯一,要进行判断取舍。
在已知三边和一个角的情况下:求另一个角
思考
我们讨论的解三角形的问题可以分为几种类型?分别是怎样求解的?
1.余弦定理
a
=b
+c-2bccosA
b
=c
+a-2accosB
c
=a
+b-2abcosC
2
2
2
2
2
2
2
2
2
4.余弦定理可以解决有关三角形的问题:
(1)已知三边,求三个角;
(2)已知两边和它们的夹角,求
第三边和其它两角;
(3)判断三角形的形状。
3.余弦定理及勾股定理关系
七、小结
2.余弦定理的推论
八、课后作业
读书部分:阅读课本第8、9页探究与发现
书面作业:优化设计第5页(必做)
优化设计第4页例题与反思
谢谢!
余弦定理
一、复习回顾
1、回顾正弦定理以及正弦定理能解决的解三角形
问题的类型。
?
(1)已知两个角和一条边
(2)已知两条边和一边的对角
正弦定理:
正弦定理能解决的问题类型:
二、创设情境
兴趣导入
A·
·
B
A.
.B
120°
500m
300m
A
B
C
120°
500m
300m
?
C
.
二、创设情境
兴趣导入
二、创设情境
兴趣导入
1、如何用初中的三角方法来求AB的长
2、如何边、角为一般的结论是否成立
如图,
三、向量法证明余弦定理
由向量的减法,
A
B
C
?
自
主
探
究
1、若已知△ABC中两边长a,b和角C,求角C的对边边长c。
2、若已知△ABC中两边长b
,
c和角A,求角A的对边边长a。
A
C
B
a
c
b
3、若已知△ABC中两边长a
,
c和角B,求角B的对边边长b
。
余弦定理:三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍。
a
=b
+c-2bccosA
b
=c
+a-2cacosB
c
=a
+b-2abcosC
2
2
2
2
2
2
2
2
2
应用余弦定理,我们就可以从已知的两边和夹角计算出三角形的第三条边。
知三求一
从余弦定理,可以得到它的推论
四、余弦定理的推论
B
ac
c
a
b
cos
2
2
2
2
-
+
=
思考
如果已知三角形的三边,如何确定三个角?
余弦定理的推论:
四、余弦定理的推论
应用余弦定理的推论,我们就可以从三角形的三边计算出三角形的三个角。
勾股定理指出了直角三角形中三边平方之间的关系,余弦定理则指出了一般三角形中三边平方之间的关系,如何看这两个定理之间的关系?
C为锐角
余弦定理可以看作是勾股定理的推广,勾股定理是余弦定理的特例
cosC>0
C为直角
cosC=0
cosC<0
C为钝角
五、巩固知识
典型例题
例1:在三角形ABC中,C=120°,b=500,a=300,求c及sinA,sinB
情景题
A
B
C
?
500
300
120°
例2:在△ABC中,已知a=2,
,
,求A。
C
B
A
a=2
例3:在△ABC中,已知a=2,
,
,解三角形。
C
B
A
a=2
练习2:在△ABC中,已知b=3,
,
B=30°,解三角形
六、巩固知识
随堂练习
练习1:在△ABC中,c=3,A=45°,B=75°,求a
练习3:在△ABC中,已知a=5,b=7,c=8,则△ABC(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
思考
在解三角形的过程中,求某一个角有时既可以用余弦定理,也可以用正弦定理,两种方法有什么利弊呢?
(2)用余弦定理推论,解唯一,可以免去判断取舍。
(1)用正弦定理,计算相对简单,但解不唯一,要进行判断取舍。
在已知三边和一个角的情况下:求另一个角
思考
我们讨论的解三角形的问题可以分为几种类型?分别是怎样求解的?
1.余弦定理
a
=b
+c-2bccosA
b
=c
+a-2accosB
c
=a
+b-2abcosC
2
2
2
2
2
2
2
2
2
4.余弦定理可以解决有关三角形的问题:
(1)已知三边,求三个角;
(2)已知两边和它们的夹角,求
第三边和其它两角;
(3)判断三角形的形状。
3.余弦定理及勾股定理关系
七、小结
2.余弦定理的推论
八、课后作业
读书部分:阅读课本第8、9页探究与发现
书面作业:优化设计第5页(必做)
优化设计第4页例题与反思
谢谢!
