9.1.1不等式及其解集(共28张ppt)
文档属性
| 名称 | 9.1.1不等式及其解集(共28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 702.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
不等式及其解集
第九章
不等式与不等式组
教学目标
了解不等式概念,理解不等式的解和解集.
教学重点
教学难点
不等式及解集概念的理解.
不等式及解集概念的理解.
现实世界中存在大量的数量关系,包括相等关系和不等关系.用等式(包括方程),我们可以研究相等关系,而研究不等关系需要用本章的不等式.
前言
思考
一辆匀速行驶的汽车在11:20距离A地50
km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
(1)汽车在12:00之前驶过A地的意思是什么?
从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50
km所用的时间不到?
?
?
?
.
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶?
?
的路程要超过50
km.
思考
一辆匀速行驶的汽车在11:20距离A地50
km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
(2)如何用式子表示以上不等关系?
设:车速为x
km/h.
像?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?这样,用符号“<”或“>”表示大小关系的式子,叫不等式.
不等式的概念
像a+2≠a-2这样用“≠”表示的不等关系的式子也是不等式.
不等式的符号统称不等号,有
“>”
“<”
“≠”,
其中“≤”
“≥”也是不等号.
例题
下列式子哪些是不等式?
①
-1<3
⑥
2m
<n
⑤
2x
-3
④
6
>2
③
3x
≠
4y
②
-x+2=4
是??
不是
是??
是??
不是
是??
练习
其中不等式有(?
?
?
?)
B
练习
下列式子哪些是不等式?哪些不是不等式?
答案:①②③⑤⑦⑧是不等式,④⑥不是.
虽然这两个式子表示了车速要满足的条件,但是我们往往希望更明确地得出
x
的取值.
思考
车速可以是每小时80千米吗??
车速可以是每小时72千米吗?
车速可以是每小时75千米吗?
车速可以是每小时78千米吗?
不等式的解
与方程的解类似,我们把使不等式成立的未知数的值叫做不等式的解.
思考
不等式的解集
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
求不等式的解集的过程叫做解不等式.
例题
请用不等式表示:
?
(3)
a
的一半大于3.
(2)
a
与5的和小于-7;
(1)
a
是负数;
例题
(?
?
?
?)
(?
?
?
?)
(?
?
?
?)
练习
1.用不等式表示:
(1)a
是正数;
(2)a
是负数;
(3)a
与
5
的和小于
7;
(4)a
与
2
的差大于
-1;
(5)a
的4
倍大于
8;
(6)a
的一半小于
3.
练习
2.
下列数中哪些是不等式
x+3>6
的解?哪些不是?
-4,-2,5,0,1,2.5,3.2,4.8,8,12
.
练习
3.直接说出不等式的解集:
练习
下列说法正确的是(?
?
?
?)
A
除了用不等式?x>75?表示解集,还有其他表示方法吗???
解集的数轴表示
还可以用数轴表示不等式的解集
画空心表示不包含75这个点
例题
用数轴表示下列不等式的解集:
(1)
x
>-1;
(2)x
≥
-1;
(3)x
<
-1;(4)x
≤
-1
.
总结:
①用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
②用数轴表示不等式的解集,,应记住下面的规律:
大于向右画,小于向左画;
有等号(≥
,≤)画实心点,无等号(>,<)画空心圆.
解:
例题
不等式
x+1≥-1的解集为:
x
≥
-2
定方向
画数轴?
?
定点
例题
注意:在数轴上表示-2
的点的位置上,应画实心圆心,表示包括这一点.
练习
写出下列数轴所表示的不等式的解集:
x
>
-3?
x
≤
a
x
<
-3
x
≥
2
练习
直接说出不等式的解集,并在数轴上表示出来.?
?
(1)x>3
(2)x<-2
总结
这节课我们学会了什么?
1.不等式的概念:
像?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?这样,用符号“<”或“>”表示大小关系的式子,叫不等式.
2.不等式的解集:
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
3.不等式的解集的数轴表示:
总结
这节课我们学会了什么?
不等式的解集一般来说有以下四种情况:
(1)
x
>
a
(2)
x
<
a
(3)
x
≥
a
(4)
x
≤
a
空心??
实心
大于往右走
小于往左走
步骤:
①画数轴
②定界点
③定方向
不等式及其解集
第九章
不等式与不等式组
教学目标
了解不等式概念,理解不等式的解和解集.
教学重点
教学难点
不等式及解集概念的理解.
不等式及解集概念的理解.
现实世界中存在大量的数量关系,包括相等关系和不等关系.用等式(包括方程),我们可以研究相等关系,而研究不等关系需要用本章的不等式.
前言
思考
一辆匀速行驶的汽车在11:20距离A地50
km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
(1)汽车在12:00之前驶过A地的意思是什么?
从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50
km所用的时间不到?
?
?
?
.
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶?
?
的路程要超过50
km.
思考
一辆匀速行驶的汽车在11:20距离A地50
km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
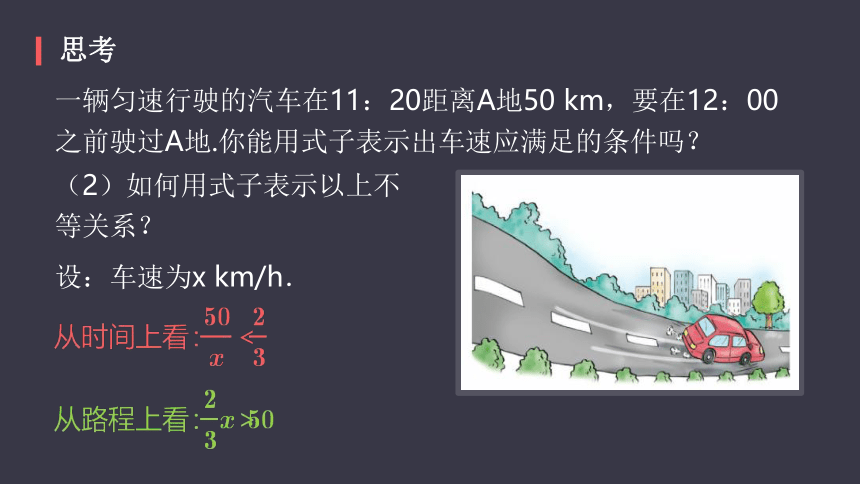
(2)如何用式子表示以上不等关系?
设:车速为x
km/h.
像?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?这样,用符号“<”或“>”表示大小关系的式子,叫不等式.
不等式的概念
像a+2≠a-2这样用“≠”表示的不等关系的式子也是不等式.
不等式的符号统称不等号,有
“>”
“<”
“≠”,
其中“≤”
“≥”也是不等号.
例题
下列式子哪些是不等式?
①
-1<3
⑥
2m
<n
⑤
2x
-3
④
6
>2
③
3x
≠
4y
②
-x+2=4
是??
不是
是??
是??
不是
是??
练习
其中不等式有(?
?
?
?)
B
练习
下列式子哪些是不等式?哪些不是不等式?
答案:①②③⑤⑦⑧是不等式,④⑥不是.
虽然这两个式子表示了车速要满足的条件,但是我们往往希望更明确地得出
x
的取值.
思考
车速可以是每小时80千米吗??
车速可以是每小时72千米吗?
车速可以是每小时75千米吗?
车速可以是每小时78千米吗?
不等式的解
与方程的解类似,我们把使不等式成立的未知数的值叫做不等式的解.
思考
不等式的解集
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
求不等式的解集的过程叫做解不等式.
例题
请用不等式表示:
?
(3)
a
的一半大于3.
(2)
a
与5的和小于-7;
(1)
a
是负数;
例题
(?
?
?
?)
(?
?
?
?)
(?
?
?
?)
练习
1.用不等式表示:
(1)a
是正数;
(2)a
是负数;
(3)a
与
5
的和小于
7;
(4)a
与
2
的差大于
-1;
(5)a
的4
倍大于
8;
(6)a
的一半小于
3.
练习
2.
下列数中哪些是不等式
x+3>6
的解?哪些不是?
-4,-2,5,0,1,2.5,3.2,4.8,8,12
.
练习
3.直接说出不等式的解集:
练习
下列说法正确的是(?
?
?
?)
A
除了用不等式?x>75?表示解集,还有其他表示方法吗???
解集的数轴表示
还可以用数轴表示不等式的解集
画空心表示不包含75这个点
例题
用数轴表示下列不等式的解集:
(1)
x
>-1;
(2)x
≥
-1;
(3)x
<
-1;(4)x
≤
-1
.
总结:
①用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
②用数轴表示不等式的解集,,应记住下面的规律:
大于向右画,小于向左画;
有等号(≥
,≤)画实心点,无等号(>,<)画空心圆.
解:
例题
不等式
x+1≥-1的解集为:
x
≥
-2
定方向
画数轴?
?
定点
例题
注意:在数轴上表示-2
的点的位置上,应画实心圆心,表示包括这一点.
练习
写出下列数轴所表示的不等式的解集:
x
>
-3?
x
≤
a
x
<
-3
x
≥
2
练习
直接说出不等式的解集,并在数轴上表示出来.?
?
(1)x>3
(2)x<-2
总结
这节课我们学会了什么?
1.不等式的概念:
像?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?这样,用符号“<”或“>”表示大小关系的式子,叫不等式.
2.不等式的解集:
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
3.不等式的解集的数轴表示:
总结
这节课我们学会了什么?
不等式的解集一般来说有以下四种情况:
(1)
x
>
a
(2)
x
<
a
(3)
x
≥
a
(4)
x
≤
a
空心??
实心
大于往右走
小于往左走
步骤:
①画数轴
②定界点
③定方向
