广东省汕头市澄海高级中学校2020-2021学年高一下学期3月第一次学段考试数学试题 Word版含答案解析
文档属性
| 名称 | 广东省汕头市澄海高级中学校2020-2021学年高一下学期3月第一次学段考试数学试题 Word版含答案解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 558.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览




文档简介
澄海中学2020-2021学年度第二学期第一次学段考试
高一级数学科试卷
本试卷分选择题和非选择题两部分,共3页,满分150分.考试时间120分钟.
注意事项:
1.答第I卷前,务必将自己的姓名、座位号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.
3.考试结束后,监考人将答题卡收回,试卷考生自己保管.
第一部分(选择题,共60分)
一、单项选择题:本大题共有8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把它选出后在答题卡规定的位置上用铅笔涂黑.
1.集合A={﹣3,﹣2,﹣1,0,1,2},集合B={x||2x﹣1|<2},则A∩B=( )
A.{﹣1,0,1}
B.{0,1,2}
C.{0,1}
D.?
2.
已知,则“”是“”的(
)
A.
充分而不必要条件
B.
必要而不充分条件
C.
充分必要条件
D.
既不充分也不必要条件
3.
已知函数,则函数的定义域为(
)
A.
B.
C.
D.
4.
若,,,则??的大小关系为(
)
A.
B.
C.
D.
5.
中国5G技术领先世界,5G技术的数学原理之一便是著名的香农公式:,它表示:在受噪声干扰的信道中,最大信息传递速率取决于信道带宽、信道内信号的平均功率、信道内部的高斯噪声功率的大小,其中叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计,按照香农公式,若不改变带宽,而将信噪比从1000提升至5000,则大约增加了(
)
附:
A.
20%
B.
23%
C.
28%
D.
50%
6.在△ABC中,,E为AD的中点,则等于( )
A.
B.
C.
D.
7.已知false,false,false,点false在false上,
且false,设falsefalse,则false等于(
)
A.false
B.false
C.false
D.
false
8.在false中,角false的对边分别为false,若false为锐角三角形,
且满足,false,则等式成立的是(
)
A.false
B.false
C.false
D.false
二、多项选择题:本大题共有4小题,每小题5分,共20分,在每小题给出的四个选项中,有多个选项是符合题目要求的,请把它选出后在答题卡规定的位置上用铅笔涂黑.(选对得5分,选漏得2分,有一个错得0分)
9.下列叙述中错误的是(
)
A.若false,则false
B.若false,则false与false的方向相同或相反
C.若false,false,则false
D.对任一向量false,false是一个单位向量
10.
若,,且,则下列不等式恒成立的是(
)
A.
B.
C.
D.
11.下列函数既是奇函数又是增函数的是(
)
A.
B.f(x)=tanx
C.f(x)=3x﹣3﹣x
D.f(x)=x?cosx
12.
为R上的偶函数,,,
且,令,下列结论正确的是(
)
A.
函数在R上是单调函数
B.
若a+b=2,则
C.
D.
方程所有根的和为2
第二部分(非选择题,共90分)
三、填空题:本大题共有4个小题,每小题5分,共20分。把答案填在答题卷相应横线上.
13.
不等式的解集为___________.
14.
设函数(其中)k是的小数点后的第n位数字,
=3.1415926535,则___________.
若函数且在上最大值为,
最小值为,函数在上是增函数,则的值是______.
已知对满足的任意正实数x,y,都有,
则实数a的取值范围为___________.
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.
温馨提示:
考生请注意在答题卷规定区域内用黑色笔作答,超出指定区域答题不给分.
17.(本小题满分10分)已知向量、.
(1)求向量与的夹角
的大小;
(2)若向量,求实数t的值;[]
(3)若向量满足,求的值.
18.(本小题满分12分)已知false为false的三内角,
且其对边分别为false,若false.
(1)求false;(2)若false,false,求false的面积.
19.(本小题满分12分)已知false,
(1)求函数在R上的单调递减区间;
(2)求函数false上的值域;(3)求不等式false在false上的解集
20.(本小题满分12分)
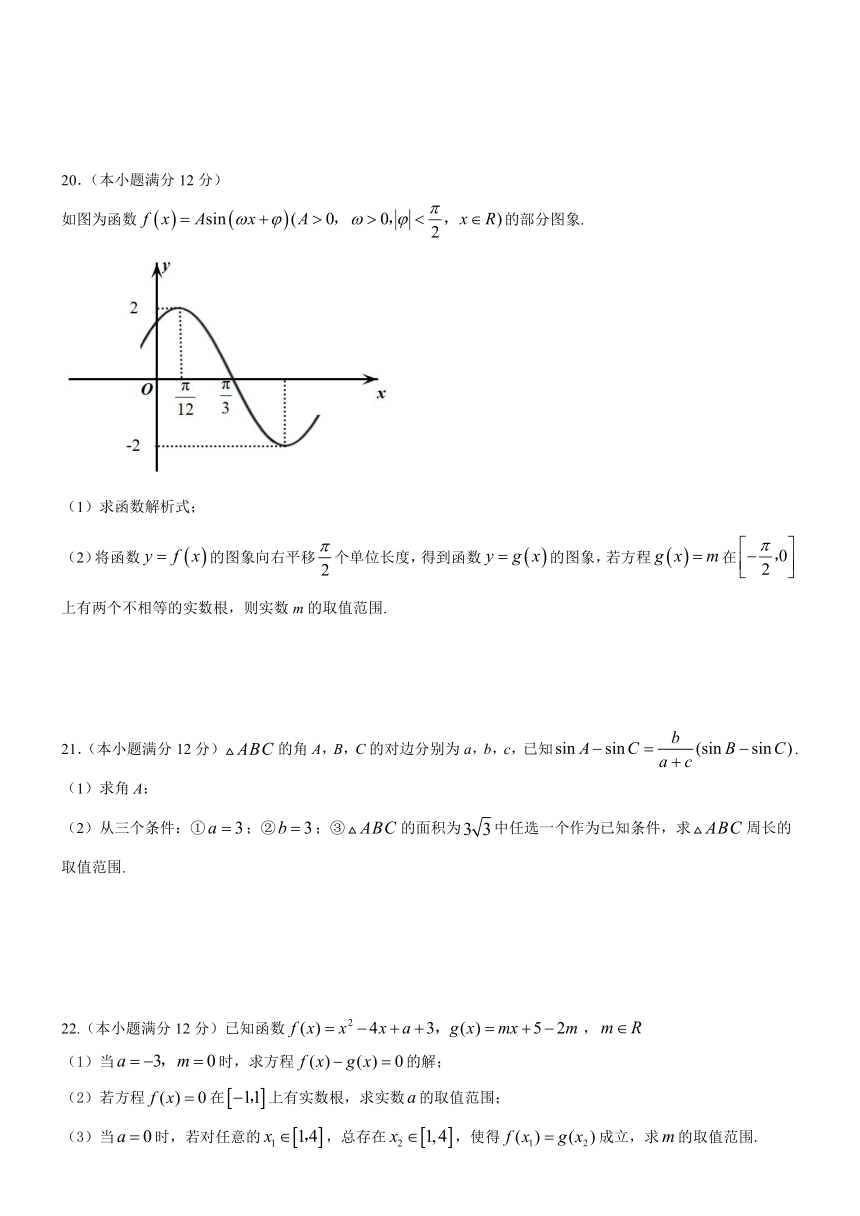
如图为函数false的部分图象.
(1)求函数解析式;
(2)将函数false的图象向右平移false个单位长度,得到函数false的图象,若方程false在false上有两个不相等的实数根,则实数m的取值范围.
21.(本小题满分12分)false的角A,B,C的对边分别为a,b,c,已知false.
(1)求角A;
(2)从三个条件:①false;②false;③false的面积为false中任选一个作为已知条件,求false周长的取值范围.
22.(本小题满分12分)已知函数false,false
当false时,求方程false的解;
若方程false在false上有实数根,求实数false的取值范围;
当false时,若对任意的false,总存在false,使得false成立,求false的取值范围.
澄海中学2020-2021学年度第二学期第一次学段考试答案
1.解:因为集合A={﹣3,﹣2,﹣1,0,1,2},集合B={x||2x﹣1|<2}={x|},
所以A∩B={0,1}.故选:C.
2.
解:当,时,,但;当,时,,但;综上,“”是“”的既不充分也不必要条件,故选:D.
3.
解:要使函数有意义,则有解得
所以函数的定义域为故选:A
4.
解:,,,所以.故选:B.
5.
解:将信噪比从1000提升至5000时,增加比率为
.故选:.
6.
7.
解:依题意得false,false,false,
即false,由正弦定理得false,选B.
9.下列叙述中错误的是(
ABD
)
A.若false,则false
B.若false,则false与false的方向相同或相反
C.若false,false,则false
D.对任一向量false,false是一个单位向量
10.
【详解】,当且仅当时取等号,A正确;
,,,当且仅当时取等号,B正确,
C错误,
,D错误.故选AB.
11.解:A.f(x)=的定义域为R,是奇函数,且是增函数,满足条件,
B.f(x)=tanx是奇函数,在定义域上不是增函数,不满足条件,
C.f(﹣x)=3﹣x﹣3x=﹣(3x﹣3﹣x)=﹣f(x),
则函数f(x)是奇函数,在R上是增函数,满足条件,
D.f(﹣x)=﹣xcos(﹣x)=﹣xcosx=﹣f(x),则f(x)是奇函数,
f(0)=0,f(π)=﹣π,则f(x)不是增函数,不满足条件.故选:AC.
12.
【详解】因为,,
所以在上单调递增
令,因为为R上的偶函数,所以为R上的奇函数
因为,在上单调递增,为R上的奇函数,
所以在R上单调递增,
将的图象向右平移1个单位,再向上平移1010个单位可得的图象
所以的图象关于点对称,所以若a+b=2,则,B正确
,故C错误
因为函数的图象和函数都关于对称,
所以它们的交点也关于对称,
所以方程所有根的和为2,故D正确
由于平移不改变单调性,所以在R上单调递增,故A正确.故选:ABD
13.
解:同解于,解得:或
即原不等式的解集为.故答案为:
14.
设函数(其中)k是的小数点后的第n位数字,=3.1415926535,则____3_______.
解:函数(其中)k是的小数点后的第n位数字,=3.1415926535,
所以,,,故答案为:.
15.
若函数且在上最大值为,最小值为,函数在上是增函数,则的值是__1____.
解:当时,函数是正实数集上的增函数,
而函数在上的最大值为,
因此有,
所以,此时在上是增函数,
符合题意,因此;
当时,函数是正实数集上的减函数,
而函数在上的最大值为,
因此有,
所以,此时在上是减函数,不符合题意.
故答案为:1
解:依题意,则,
,
当且仅当时等号成立.
由,为正实数得
,,
令,在上递增,所以时有最小值,
所以.故答案为:
四、解答题:
解:(1)
、
………………………………2分
………………………………4分
(2)∵、,
.………………………………5分
,∴t(t﹣1)﹣(1﹣t)=0,………………………………6分
解得t=1或t=﹣1;………………………………7分
(3)∵,∴(x,y)=(y,y+1﹣x),…………8分
即,………………………………9分
解得.∴.………………………………10分
解:(1)∵false,
∴由正弦定理可得:false………………………1分,
整理得false………………………2分,
即:false………………………3分,
所以false………………………4分,
∵false,∴false………………………5分,
∵false,∴false………………………6分.
(2)由false,false,由余弦定理得false,
∴false………………………9分,
即有false,
∴false………………………………………………………10分,
∴false的面积为false……………………………12分.
19.解:(1)因为false,
......................1分
令false,解得:false......................3分
即函数false的单调减区间为false,
......................4分
(2)false
...........................5分
false
...........................6分
false
(3)false
false
false
false,故不等式的解集为false
解(1)由题中的图象知,false,false,
所以false,false……………………………2分,
因为图象过点false,所以false,
解得false……………………………4分,,
false,false……………………………5分,
函数解析式为false……………………………6分;
(2)由题意得false
∵,,……………………………7分,
令
问题转化为有两个不相等的实数根…………………9分,
画出的图象,并取部分图象如图所示
…………10分,
由函数的图象可知,false时,有两个不同的实根…………………………12分.
解(1)因为false,
所以false,……………………………1分,
得false……………………………2分,
所以false……………………………3分,
因为false,所以false.……………………………4分,
(2)分三种情况求解:
选择①false,因为false,
由正弦定理得false……………………………6分,
即false的周长false……………………………7分,
false……………………………8分,
false……………………………9分,
false……………………………10分,
因为,所以,∴…………………11分,
即false周长的取值范围是false…………………12分,
选择②false,因为false,
由正弦定理得false……………………………6分,
false……………………………8分,
即false的周长false
false
false,…………10分,
因为false,所以false,所以false,
即false周长的取值范围是false.……………………………12分,
选择③false.
因为false,得false………………………6分,
由余弦定理得false…………………8分,
即false的周长false,
因为,当且仅当false时等号成立………………………10分
所以
+=
即false周长的取值范围是false.………………………12分
解:(1)当false时,false
令false解得false或false.......................................................2分
(2)false的对称轴为false,要使得false在false上有零点,
需满足false.....................4分
即false
............................5分
解得false.....................................................................6分
若对任意的false,总存在false,使得false成立,
只需函数false的值域为函数false的值域的子集......................................7分
false时,false的值域为false.........................................8分
下求false的值域
①当false时,false,不符合题意舍去;.......................................................................9分
②当false时,false的值域为false
要使false,需满足false,解得false...............................10分
③当false时,false的值域为false
要使false,需满足false,解得false...........................11分
综上所述,false或false........................................................................12分
高一级数学科试卷
本试卷分选择题和非选择题两部分,共3页,满分150分.考试时间120分钟.
注意事项:
1.答第I卷前,务必将自己的姓名、座位号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.
3.考试结束后,监考人将答题卡收回,试卷考生自己保管.
第一部分(选择题,共60分)
一、单项选择题:本大题共有8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把它选出后在答题卡规定的位置上用铅笔涂黑.
1.集合A={﹣3,﹣2,﹣1,0,1,2},集合B={x||2x﹣1|<2},则A∩B=( )
A.{﹣1,0,1}
B.{0,1,2}
C.{0,1}
D.?
2.
已知,则“”是“”的(
)
A.
充分而不必要条件
B.
必要而不充分条件
C.
充分必要条件
D.
既不充分也不必要条件
3.
已知函数,则函数的定义域为(
)
A.
B.
C.
D.
4.
若,,,则??的大小关系为(
)
A.
B.
C.
D.
5.
中国5G技术领先世界,5G技术的数学原理之一便是著名的香农公式:,它表示:在受噪声干扰的信道中,最大信息传递速率取决于信道带宽、信道内信号的平均功率、信道内部的高斯噪声功率的大小,其中叫做信噪比.当信噪比比较大时,公式中真数中的1可以忽略不计,按照香农公式,若不改变带宽,而将信噪比从1000提升至5000,则大约增加了(
)
附:
A.
20%
B.
23%
C.
28%
D.
50%
6.在△ABC中,,E为AD的中点,则等于( )
A.
B.
C.
D.
7.已知false,false,false,点false在false上,
且false,设falsefalse,则false等于(
)
A.false
B.false
C.false
D.
false
8.在false中,角false的对边分别为false,若false为锐角三角形,
且满足,false,则等式成立的是(
)
A.false
B.false
C.false
D.false
二、多项选择题:本大题共有4小题,每小题5分,共20分,在每小题给出的四个选项中,有多个选项是符合题目要求的,请把它选出后在答题卡规定的位置上用铅笔涂黑.(选对得5分,选漏得2分,有一个错得0分)
9.下列叙述中错误的是(
)
A.若false,则false
B.若false,则false与false的方向相同或相反
C.若false,false,则false
D.对任一向量false,false是一个单位向量
10.
若,,且,则下列不等式恒成立的是(
)
A.
B.
C.
D.
11.下列函数既是奇函数又是增函数的是(
)
A.
B.f(x)=tanx
C.f(x)=3x﹣3﹣x
D.f(x)=x?cosx
12.
为R上的偶函数,,,
且,令,下列结论正确的是(
)
A.
函数在R上是单调函数
B.
若a+b=2,则
C.
D.
方程所有根的和为2
第二部分(非选择题,共90分)
三、填空题:本大题共有4个小题,每小题5分,共20分。把答案填在答题卷相应横线上.
13.
不等式的解集为___________.
14.
设函数(其中)k是的小数点后的第n位数字,
=3.1415926535,则___________.
若函数且在上最大值为,
最小值为,函数在上是增函数,则的值是______.
已知对满足的任意正实数x,y,都有,
则实数a的取值范围为___________.
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤.
温馨提示:
考生请注意在答题卷规定区域内用黑色笔作答,超出指定区域答题不给分.
17.(本小题满分10分)已知向量、.
(1)求向量与的夹角
的大小;
(2)若向量,求实数t的值;[]
(3)若向量满足,求的值.
18.(本小题满分12分)已知false为false的三内角,
且其对边分别为false,若false.
(1)求false;(2)若false,false,求false的面积.
19.(本小题满分12分)已知false,
(1)求函数在R上的单调递减区间;
(2)求函数false上的值域;(3)求不等式false在false上的解集
20.(本小题满分12分)
如图为函数false的部分图象.
(1)求函数解析式;
(2)将函数false的图象向右平移false个单位长度,得到函数false的图象,若方程false在false上有两个不相等的实数根,则实数m的取值范围.
21.(本小题满分12分)false的角A,B,C的对边分别为a,b,c,已知false.
(1)求角A;
(2)从三个条件:①false;②false;③false的面积为false中任选一个作为已知条件,求false周长的取值范围.
22.(本小题满分12分)已知函数false,false
当false时,求方程false的解;
若方程false在false上有实数根,求实数false的取值范围;
当false时,若对任意的false,总存在false,使得false成立,求false的取值范围.
澄海中学2020-2021学年度第二学期第一次学段考试答案
1.解:因为集合A={﹣3,﹣2,﹣1,0,1,2},集合B={x||2x﹣1|<2}={x|},
所以A∩B={0,1}.故选:C.
2.
解:当,时,,但;当,时,,但;综上,“”是“”的既不充分也不必要条件,故选:D.
3.
解:要使函数有意义,则有解得
所以函数的定义域为故选:A
4.
解:,,,所以.故选:B.
5.
解:将信噪比从1000提升至5000时,增加比率为
.故选:.
6.
7.
解:依题意得false,false,false,
即false,由正弦定理得false,选B.
9.下列叙述中错误的是(
ABD
)
A.若false,则false
B.若false,则false与false的方向相同或相反
C.若false,false,则false
D.对任一向量false,false是一个单位向量
10.
【详解】,当且仅当时取等号,A正确;
,,,当且仅当时取等号,B正确,
C错误,
,D错误.故选AB.
11.解:A.f(x)=的定义域为R,是奇函数,且是增函数,满足条件,
B.f(x)=tanx是奇函数,在定义域上不是增函数,不满足条件,
C.f(﹣x)=3﹣x﹣3x=﹣(3x﹣3﹣x)=﹣f(x),
则函数f(x)是奇函数,在R上是增函数,满足条件,
D.f(﹣x)=﹣xcos(﹣x)=﹣xcosx=﹣f(x),则f(x)是奇函数,
f(0)=0,f(π)=﹣π,则f(x)不是增函数,不满足条件.故选:AC.
12.
【详解】因为,,
所以在上单调递增
令,因为为R上的偶函数,所以为R上的奇函数
因为,在上单调递增,为R上的奇函数,
所以在R上单调递增,
将的图象向右平移1个单位,再向上平移1010个单位可得的图象
所以的图象关于点对称,所以若a+b=2,则,B正确
,故C错误
因为函数的图象和函数都关于对称,
所以它们的交点也关于对称,
所以方程所有根的和为2,故D正确
由于平移不改变单调性,所以在R上单调递增,故A正确.故选:ABD
13.
解:同解于,解得:或
即原不等式的解集为.故答案为:
14.
设函数(其中)k是的小数点后的第n位数字,=3.1415926535,则____3_______.
解:函数(其中)k是的小数点后的第n位数字,=3.1415926535,
所以,,,故答案为:.
15.
若函数且在上最大值为,最小值为,函数在上是增函数,则的值是__1____.
解:当时,函数是正实数集上的增函数,
而函数在上的最大值为,
因此有,
所以,此时在上是增函数,
符合题意,因此;
当时,函数是正实数集上的减函数,
而函数在上的最大值为,
因此有,
所以,此时在上是减函数,不符合题意.
故答案为:1
解:依题意,则,
,
当且仅当时等号成立.
由,为正实数得
,,
令,在上递增,所以时有最小值,
所以.故答案为:
四、解答题:
解:(1)
、
………………………………2分
………………………………4分
(2)∵、,
.………………………………5分
,∴t(t﹣1)﹣(1﹣t)=0,………………………………6分
解得t=1或t=﹣1;………………………………7分
(3)∵,∴(x,y)=(y,y+1﹣x),…………8分
即,………………………………9分
解得.∴.………………………………10分
解:(1)∵false,
∴由正弦定理可得:false………………………1分,
整理得false………………………2分,
即:false………………………3分,
所以false………………………4分,
∵false,∴false………………………5分,
∵false,∴false………………………6分.
(2)由false,false,由余弦定理得false,
∴false………………………9分,
即有false,
∴false………………………………………………………10分,
∴false的面积为false……………………………12分.
19.解:(1)因为false,
......................1分
令false,解得:false......................3分
即函数false的单调减区间为false,
......................4分
(2)false
...........................5分
false
...........................6分
false
(3)false
false
false
false,故不等式的解集为false
解(1)由题中的图象知,false,false,
所以false,false……………………………2分,
因为图象过点false,所以false,
解得false……………………………4分,,
false,false……………………………5分,
函数解析式为false……………………………6分;
(2)由题意得false
∵,,……………………………7分,
令
问题转化为有两个不相等的实数根…………………9分,
画出的图象,并取部分图象如图所示
…………10分,
由函数的图象可知,false时,有两个不同的实根…………………………12分.
解(1)因为false,
所以false,……………………………1分,
得false……………………………2分,
所以false……………………………3分,
因为false,所以false.……………………………4分,
(2)分三种情况求解:
选择①false,因为false,
由正弦定理得false……………………………6分,
即false的周长false……………………………7分,
false……………………………8分,
false……………………………9分,
false……………………………10分,
因为,所以,∴…………………11分,
即false周长的取值范围是false…………………12分,
选择②false,因为false,
由正弦定理得false……………………………6分,
false……………………………8分,
即false的周长false
false
false,…………10分,
因为false,所以false,所以false,
即false周长的取值范围是false.……………………………12分,
选择③false.
因为false,得false………………………6分,
由余弦定理得false…………………8分,
即false的周长false,
因为,当且仅当false时等号成立………………………10分
所以
+=
即false周长的取值范围是false.………………………12分
解:(1)当false时,false
令false解得false或false.......................................................2分
(2)false的对称轴为false,要使得false在false上有零点,
需满足false.....................4分
即false
............................5分
解得false.....................................................................6分
若对任意的false,总存在false,使得false成立,
只需函数false的值域为函数false的值域的子集......................................7分
false时,false的值域为false.........................................8分
下求false的值域
①当false时,false,不符合题意舍去;.......................................................................9分
②当false时,false的值域为false
要使false,需满足false,解得false...............................10分
③当false时,false的值域为false
要使false,需满足false,解得false...........................11分
综上所述,false或false........................................................................12分
同课章节目录
