9.3一元一次不等式组(共37张ppt)
文档属性
| 名称 | 9.3一元一次不等式组(共37张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 743.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览










文档简介
(共37张PPT)
一元一次不等式组
回忆:
1.什么是不等式的解集?
2.求解一元一次不等式有哪些步骤?
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集。
去分母、去括号、移项、合并同类项、将未知数的系数化为1。
在数轴上表示不等式的解集时应注意:
大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.
PPT模板:www./moban/
PPT素材:www./sucai/
PPT背景:www./beijing/
PPT图表:www./tubiao/
PPT下载:www./xiazai/
PPT教程:
www./powerpoint/
资料下载:www./ziliao/
范文下载:www./fanwen/
试卷下载:www./shiti/
教案下载:www./jiaoan/
PPT论坛:www.
PPT课件:www./kejian/
语文课件:www./kejian/yuwen/
数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/
美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/
物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/
生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/
历史课件:www./kejian/lishi/
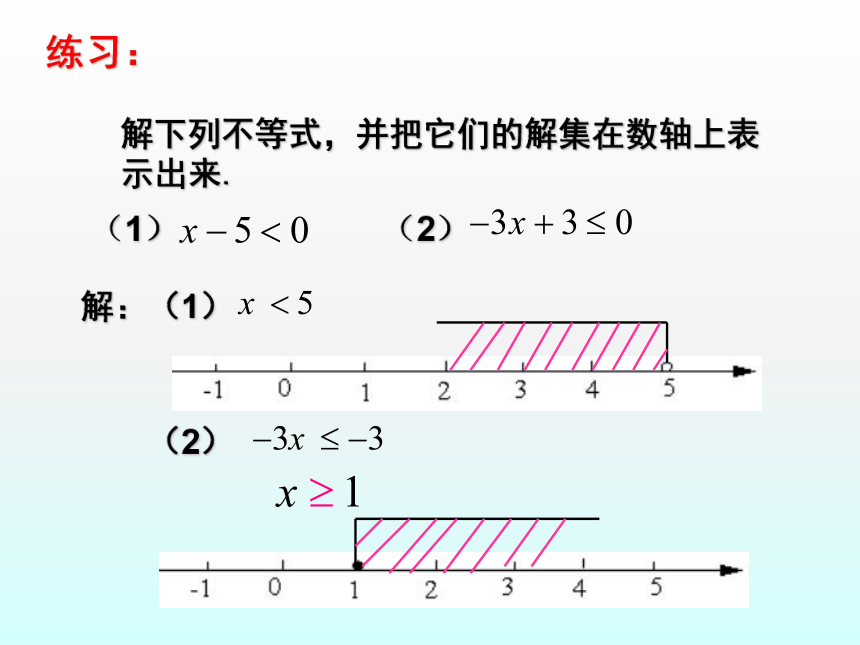
练习:
解下列不等式,并把它们的解集在数轴上表示出来.
(1)
(2)
解:
(1)
(2)
PPT模板:www./moban/
PPT素材:www./sucai/
PPT背景:www./beijing/
PPT图表:www./tubiao/
PPT下载:www./xiazai/
PPT教程:
www./powerpoint/
资料下载:www./ziliao/
范文下载:www./fanwen/
试卷下载:www./shiti/
教案下载:www./jiaoan/
PPT论坛:www.
PPT课件:www./kejian/
语文课件:www./kejian/yuwen/
数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/
美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/
物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/
生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/
历史课件:www./kejian/lishi/
(1)在直角坐标系中,当x满足什么条件时?点P(3x-9,1+x)在第二象限?
观察与思考:
3x-9<0
1+x>0
①
②
类似于方程组,把这样的两个或两个以上的不等式联立,就组成一个不等式组。
1.一元一次不等式组的概念
(1)“一元”指的是什么?
指不等式组中只含有一个未知数。
(2)“一次”指的是什么?
指不等式中未知数的次数为1.
(3)
概念
由几个含有同一个未知数的一元一次不等式
不等式组叫做一元一次不等式组。
所组成的
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
观察与思考
如何解此不等式组呢?
分析
类比方程组的解,怎样确定
不等式组中X的取值范围呢?
不等式组中的各不等式解集的公共部分,
就是不等式组中X的取值范围
请大家分别求出不等式组
①
②
中的两个不等式的解集。
你能说出不等式组中X的取值范围吗?
动手操作:在数轴上分别表示出不等式①
、②的解集.
2.
一元一次不等式组的解集
请大家分别求出不等式组
①
②
中的两个不等式的解集。
解不等式①,得:
解不等式②,得:
概念:
叫做这个不等式组的解集。
不等式组中所有不等式的解集的公共部分,
(3)类似地,当X满足什么条件时,点P(3x-9,1+x)在第一象限、第三象限或第四象限?
(4)你能利用数轴分别确定上面所得的一元一次不等式组的解集吗?
设a<b,你能说出下列四种情况下不等式组的解吗?用数轴试一试
设a
<
b
在数轴上表示解
不等式组的解集
X>a
X
>b
X<a
X
<b
X>a
X
<b
X<a
X
>b
a
b
a
b
a
b
a
b
X>b
X<a
无解
a<X<b
大小小大中间找
大大小小解不了
两小取小
两大取大
规律(口诀)
探究活动:
一般地,一元一次不等式组的解集的规律如图
-5
-2
0
-3
-1
-4
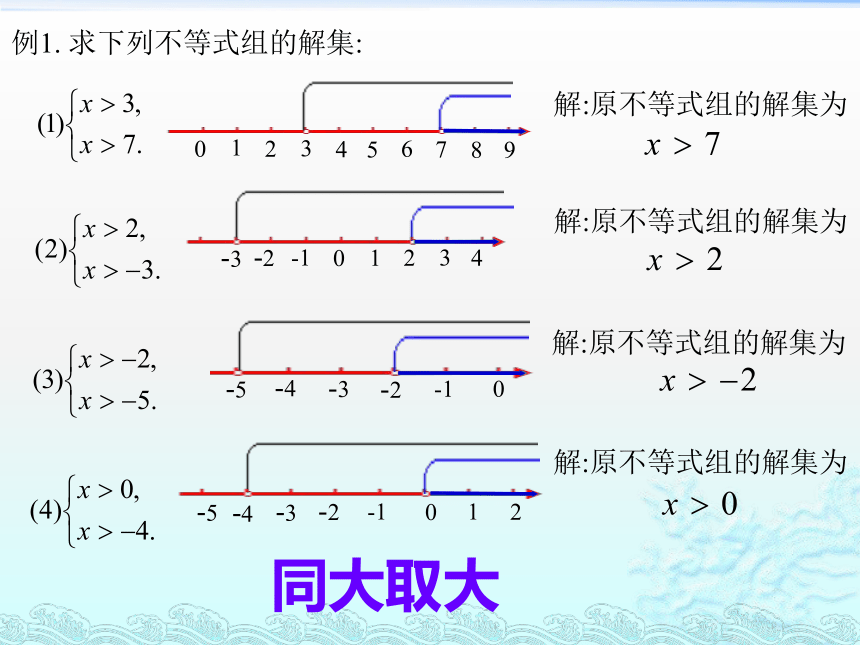
例1.
求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
同大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
例1.
求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
同小取小
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
例1.
求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小小大中间找
例1.
求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小解不了
议一议:
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的
公共部分;
(3)根据几个不等式解集的公共部分,写出
这个不等式组的解集。
根据上面的解答过程你认为解一元一次不等式组的一般步骤是什么?
例1、
解不等式组:
①
②
解:
解不等式①,得
解不等式②,得
原不等式组的解集为
练习:解下列不等式组,并把它们的解集在数轴
上表示出来:
(1)
(2)
(3)
(4)
例2、
解不等式组:
①
②
解:
由不等式①,得
由不等式②,得
原不等式组无解
1.
由几个一元一次不等式所组成的不等式组叫做一
元一次不等式组
.
2.
几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3.
求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2)
利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(一)概念
(找不到公共部分则不等式组无解)
利用规律:
同大取大,同小取小;
大小小大中间找,大大小小无解了。
练习:
题型1:已知不等式的解集,求待定字母的值或取值范围
例1:如果不等式组
有解,则m
的取值范围__________
1、已知关于x不等式组
无解,则a的取值范围是___
2、若不等式组
无解,则m的取值范围是__________。
3、关于x的不等式组
的解集为x>3,则a的取值范围是( )
A、a≥-3
B、a≤-3
C、a>-3
D、a<-3
A
m
≥2.5
a>3
练习:
例4.若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解:
解不等式①,得,x>m-2
解不等式②,得,x
<
n
+
1
因为不等式组有解,所以
m-2
<x<
n
+
1
又因为 -1<x<2
所以, m=1
, n=1
-1
2
< x <
m-2
n
+
1
m-2=
-1 ,
n
+
1
=
2
练习1:已知关于x的
不等式组
的解集为3≤x<5,
则n/m=
解:
解不等式①,得,x≥m+n
解不等式②,得,x
<(2n+m+1)÷2
因为不等式组有解,所以
m+n≤
x
<
(
2n+m+1
)÷2
又因为
3≤x<5
所以
解得
所以
n/m=4
这里也是一个含x的一元一次不等式,将m,n看作两个已知数
练习2:如果不等式组
的解是5题型2:已知不等式的整数解的个数,求待定字母的取值范围
练习
1
如果不等式组
-2<x≤4
x+m>1有4个整数解,求m的取值
范围?若无解呢?
2
若不等式组
的正整数解有3个,求x的取值范围?
题型3:方程与不等式
例1.若
<
的最小整数是方程
的解,求代数式
的值。
解:2(x+1)-5<3(x-1)+4
解得x
>-4
由题意x的最小整数解为x
=-3
将x
=-3代入方程
解得 m=2
将m=2代入代数式
=
-
11
方法:
1.解不等式,求最小整数x的值;
2.将x的值代入一元一次方程
求出m的值.
3.将m的值代入含m的代数式
2.k取何值时方程组
中的x大于1,y小于1。
3.m是什么正整数时,方程
的解是非负数
4.
已知关于x,y的方程组
x+y=2a+7
x-2y=4a-3的解为正数,且x的值小于y的值。
求a的取值范围
一元一次不等式组
回忆:
1.什么是不等式的解集?
2.求解一元一次不等式有哪些步骤?
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集。
去分母、去括号、移项、合并同类项、将未知数的系数化为1。
在数轴上表示不等式的解集时应注意:
大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.
PPT模板:www./moban/
PPT素材:www./sucai/
PPT背景:www./beijing/
PPT图表:www./tubiao/
PPT下载:www./xiazai/
PPT教程:
www./powerpoint/
资料下载:www./ziliao/
范文下载:www./fanwen/
试卷下载:www./shiti/
教案下载:www./jiaoan/
PPT论坛:www.
PPT课件:www./kejian/
语文课件:www./kejian/yuwen/
数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/
美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/
物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/
生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/
历史课件:www./kejian/lishi/
练习:
解下列不等式,并把它们的解集在数轴上表示出来.
(1)
(2)
解:
(1)
(2)
PPT模板:www./moban/
PPT素材:www./sucai/
PPT背景:www./beijing/
PPT图表:www./tubiao/
PPT下载:www./xiazai/
PPT教程:
www./powerpoint/
资料下载:www./ziliao/
范文下载:www./fanwen/
试卷下载:www./shiti/
教案下载:www./jiaoan/
PPT论坛:www.
PPT课件:www./kejian/
语文课件:www./kejian/yuwen/
数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/
美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/
物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/
生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/
历史课件:www./kejian/lishi/
(1)在直角坐标系中,当x满足什么条件时?点P(3x-9,1+x)在第二象限?
观察与思考:
3x-9<0
1+x>0
①
②
类似于方程组,把这样的两个或两个以上的不等式联立,就组成一个不等式组。
1.一元一次不等式组的概念
(1)“一元”指的是什么?
指不等式组中只含有一个未知数。
(2)“一次”指的是什么?
指不等式中未知数的次数为1.
(3)
概念
由几个含有同一个未知数的一元一次不等式
不等式组叫做一元一次不等式组。
所组成的
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
观察与思考
如何解此不等式组呢?
分析
类比方程组的解,怎样确定
不等式组中X的取值范围呢?
不等式组中的各不等式解集的公共部分,
就是不等式组中X的取值范围
请大家分别求出不等式组
①
②
中的两个不等式的解集。
你能说出不等式组中X的取值范围吗?
动手操作:在数轴上分别表示出不等式①
、②的解集.
2.
一元一次不等式组的解集
请大家分别求出不等式组
①
②
中的两个不等式的解集。
解不等式①,得:
解不等式②,得:
概念:
叫做这个不等式组的解集。
不等式组中所有不等式的解集的公共部分,
(3)类似地,当X满足什么条件时,点P(3x-9,1+x)在第一象限、第三象限或第四象限?
(4)你能利用数轴分别确定上面所得的一元一次不等式组的解集吗?
设a<b,你能说出下列四种情况下不等式组的解吗?用数轴试一试
设a
<
b
在数轴上表示解
不等式组的解集
X>a
X
>b
X<a
X
<b
X>a
X
<b
X<a
X
>b
a
b
a
b
a
b
a
b
X>b
X<a
无解
a<X<b
大小小大中间找
大大小小解不了
两小取小
两大取大
规律(口诀)
探究活动:
一般地,一元一次不等式组的解集的规律如图
-5
-2
0
-3
-1
-4
例1.
求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
同大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
例1.
求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
同小取小
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
例1.
求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小小大中间找
例1.
求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小解不了
议一议:
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的
公共部分;
(3)根据几个不等式解集的公共部分,写出
这个不等式组的解集。
根据上面的解答过程你认为解一元一次不等式组的一般步骤是什么?
例1、
解不等式组:
①
②
解:
解不等式①,得
解不等式②,得
原不等式组的解集为
练习:解下列不等式组,并把它们的解集在数轴
上表示出来:
(1)
(2)
(3)
(4)
例2、
解不等式组:
①
②
解:
由不等式①,得
由不等式②,得
原不等式组无解
1.
由几个一元一次不等式所组成的不等式组叫做一
元一次不等式组
.
2.
几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3.
求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2)
利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(一)概念
(找不到公共部分则不等式组无解)
利用规律:
同大取大,同小取小;
大小小大中间找,大大小小无解了。
练习:
题型1:已知不等式的解集,求待定字母的值或取值范围
例1:如果不等式组
有解,则m
的取值范围__________
1、已知关于x不等式组
无解,则a的取值范围是___
2、若不等式组
无解,则m的取值范围是__________。
3、关于x的不等式组
的解集为x>3,则a的取值范围是( )
A、a≥-3
B、a≤-3
C、a>-3
D、a<-3
A
m
≥2.5
a>3
练习:
例4.若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解:
解不等式①,得,x>m-2
解不等式②,得,x
<
n
+
1
因为不等式组有解,所以
m-2
<x<
n
+
1
又因为 -1<x<2
所以, m=1
, n=1
-1
2
< x <
m-2
n
+
1
m-2=
-1 ,
n
+
1
=
2
练习1:已知关于x的
不等式组
的解集为3≤x<5,
则n/m=
解:
解不等式①,得,x≥m+n
解不等式②,得,x
<(2n+m+1)÷2
因为不等式组有解,所以
m+n≤
x
<
(
2n+m+1
)÷2
又因为
3≤x<5
所以
解得
所以
n/m=4
这里也是一个含x的一元一次不等式,将m,n看作两个已知数
练习2:如果不等式组
的解是5
练习
1
如果不等式组
-2<x≤4
x+m>1有4个整数解,求m的取值
范围?若无解呢?
2
若不等式组
的正整数解有3个,求x的取值范围?
题型3:方程与不等式
例1.若
<
的最小整数是方程
的解,求代数式
的值。
解:2(x+1)-5<3(x-1)+4
解得x
>-4
由题意x的最小整数解为x
=-3
将x
=-3代入方程
解得 m=2
将m=2代入代数式
=
-
11
方法:
1.解不等式,求最小整数x的值;
2.将x的值代入一元一次方程
求出m的值.
3.将m的值代入含m的代数式
2.k取何值时方程组
中的x大于1,y小于1。
3.m是什么正整数时,方程
的解是非负数
4.
已知关于x,y的方程组
x+y=2a+7
x-2y=4a-3的解为正数,且x的值小于y的值。
求a的取值范围
