模型 2021年中考数学33个专题模型
图片预览




文档简介
专题一
角平分线相关问题模型
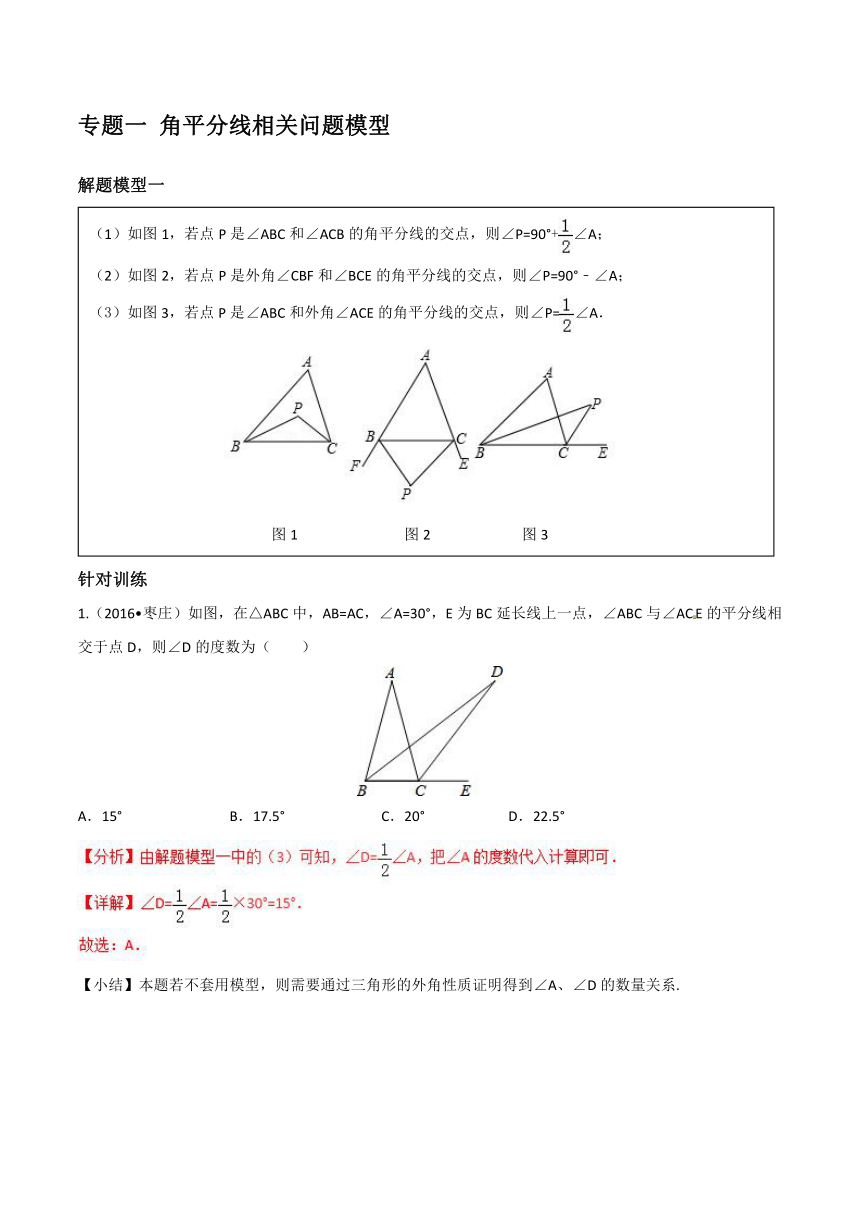
解题模型一
针对训练
1.(2016?枣庄)如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
A.15°
B.17.5°
C.20°
D.22.5°
【小结】本题若不套用模型,则需要通过三角形的外角性质证明得到∠A、∠D的数量关系.
2.(2018?巴中)如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=
.
【分析】由解题模型一中的(1)可知,∠BOC=90°+∠A,把∠BOC=110°代入计算可得到∠A的度数.
【详解】∵∠BOC=90°+∠A,∠BOC=110°,∴90°+∠A=110°.∴∠A=40°.
【小结】本题若不套用模型,需要利用三角形的内角和定理、角平分线的定义得到∠BOC、∠A的数量关系.
3.(2018?深圳)在Rt△ABC中,∠C=90°,AD平分∠CAB,BE平分∠ABC,AD、BE相交于点F,且AF=4,EF=,则AC= .
∵AD平分∠CAB,BE平分∠ABC,∴CF是∠ACB的平分线.∴∠ACF=45°=∠AFE.
∵∠CAF=∠FAE,∴△AEF∽△AFC.∴.∴AC===,故答案为.
【小结】此题主要考查了角平分线定义,勾股定理,相似三角形的判定和性质,求出AE是解本题的关键.
4.(2018?济南历城区模拟)如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2018=
.
【详解】∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
【小结】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义,熟记性质然后推出后一个角是前一个角的一半是解题的关键。
解题模型二
针对训练
5.(2018?长春)如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为( )
A.44°
B.40°
C.39°
D.38°
【小结】此题考查三角形内角和问题,关键是根据三角形内角和、角平分线的定义和平行线的性质详解.
6.(2016?湖州)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8
B.6
C.4
D.2
【分析】过点P作PE⊥BC于E,根据角平分线上的点到角的两边的距离相等可得PA=PE,PD=PE,那么PE=PA=PD,又AD=8,进而求出PE=4
【详解】过点P作PE⊥BC于点E.
∵AB∥CD,PA⊥AB,∴PD⊥CD.
∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE.,∴PE=PA=PD.
∵PA+PD=AD=8,∴PA=PD=4.∴PE=4.故选:C.
【小结】本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并作辅助线是解题的关键.
7.(2018?常德)如图,已知BD是△ABC的角平分线,ED是BC的垂直平分线,∠BAC=90°,AD=3,则CE的长为( )
A.6
B.5
C.4
D.3
【小结】本题考查的是线段垂直平分线的性质、直角三角形的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.
8.(2018?淄博)如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
A.4
B.6
C.
D.8
【分析】根据题意,可以求得∠B的度数,然后根据解直角三角形的知识可以求得NC的长,从而可以求得BC的长.
【小结】本题考查30°角的直角三角形、平行线的性质、等腰三角形的判定与性质,详解本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想详解.
9.(2018?大庆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30°
B.35°
C.45°
D.60°
【分析】作MN⊥AD于N,根据平行线的性质求出∠DAB,根据角平分线的判定定理得到∠MAB=∠DAB,计算即可
【小结】本题考查的是角平分线的判定和性质,掌握角的平分线上的点到角的两个端点的距离相等.
10.(2018?河北)如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
A.4.5
B.4
C.3
D.2
【分析】连接AI、BI,因为三角形的内心是角平分线的交点,所以AI是∠CAB的平分线,由平行的性质和等角对等边可得:AD=DI,同理BE=EI,所以图中阴影部分的周长就是边AB的长.
【小结】本题考查了三角形内心的定义、平移的性质及角平分线的定义等知识,熟练掌握三角形的内心是角平分线的交点是关键.
11.(2018?枣庄)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A.
B.
C.
D.
【分析】根据三角形的内角和定理得出∠CAF+∠CFA=90°,∠FAD+∠AED=90°,根据角平分线和对顶角相等得出∠CEF=∠CFE,即可得出EC=FC,再利用相似三角形的判定与性质得出答案.
【详解】过点F作FG⊥AB于点G,如图所示.
∴BC=4,∴=
∵FC=FG,∴=,解得FC=,
即CE的长为.故选:A.
【小结】本题考查了直角三角形性质、等腰三角形的性质和判定,三角形的内角和定理以及相似三角形的判定与性质等知识,关键是推出∠CEF=∠CFE.
12.(2017?滨州)如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )
A.4
B.3
C.2
D.1
在△POE和△POF中,,∴△POE≌△POF(HL).∴OE=OF.
在△PEM和△PFN中,,∴△PEM≌△PFN(ASA).∴EM=NF,PM=PN,故(1)正确.
∴S△PEM=S△PNF,∴S四边形PMON=S四边形PEOF=定值,故(3)正确.∵OM+ON=OE+ME+OF﹣NF=2OE=定值,故(2)正确,MN的长度是变化的,故(4)错误.,故选:B.
【小结】本题考查全等三角形的性质、角平分线的性质定理、四边形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
13.(2018?德州)如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为 3 .
【小结】此题主要考查了角平分线的性质,关键是掌握角的平分线上的点到角的两边的距离相等.
14.(2018?广安)如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF= 2 .
【分析】作EH⊥OA于点H,根据角平分线的性质求出EH,根据直角三角形的性质求出EF,根据等腰三角形的性质详解.
【详解】作EH⊥OA于点H,如图所示.
【小结】本题考查的是角平分线的性质、平行线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
15.(2018?桂林)如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是 3 .
【答案】3
【分析】首先根据已知条件分别计算图中每一个三角形每个角的度数,然后根据等腰三角形的判定:等角对等边详解,做题时要注意,从最明显的找起,由易到难,不重不漏
【小结】本题考查了等腰三角形的性质及等腰三角形的判定,角的平分线的性质;求得各个角的度数是正确详解本题的关键.
16.(2016?长春)感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)
【分析】探究:欲证明DB=DC,只要证明△DFC≌△DEB即可.
应用:先证明△DFC≌△DEB,再证明△ADF≌△ADE,结合BD=EB即可解决问题.
【详解】探究:证明:如图②中,DE⊥AB于E,DF⊥AC于F,]
∵DA平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD.
在△DFC和△DEB中,,∴△DFC≌△DEB(AAS).∴DC=DB.
∴AB﹣AC=a.故答案为a.
【小结】本题考查全等三角形的判定和性质、角平分线的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.
专题二
全等三角形解题模型
解题模型一
平移模型
针对训练
1.(2018?桂林)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
【分析】(1)求出AC=DF,根据SSS推出△ABC≌△DEF.
(2)由(1)中全等三角形的性质得到:∠A=∠EDF,进而得出结论即可.
【小结】本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应角相等.
解题模型二
对称模型
针对训练
2.(2018?南充)如图,已知AB=AD,AC=AE,∠BAE=∠DAC.
求证:∠C=∠E.
【分析】由∠BAE=∠DAC可得到∠BAC=∠DAE,再根据“SAS”可判断△BAC≌△DAE,根据全等的性质即可得到∠C=∠E.
【小结】本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应角相等,对应边相等.
3.(2018?广州)如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.
【分析】根据AE=EC,DE=BE,∠AED和∠CEB是对顶角,利用SAS证明△ADE≌△CBE即可.
【解答】证明:在△AED和△CEB中,
,
∴△AED≌△CEB(SAS).
∴∠A=∠C(全等三角形对应角相等).
【小结】此题主要考查学生对全等三角形的判定与性质这一知识点的理解和掌握,此题难度不大,要求学生应熟练掌握.
4.(2018?乐山)如图,已知∠1=∠2,∠3=∠4,求证:BC=BD.
【分析】由∠3=∠4可以得出∠ABD=∠ABC,再利用ASA就可以得出△ADB≌△ACB,就可以得出结论.
【小结】本题考查了等角的补角相等的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.
5.(2017?郴州)已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.
【分析】由∠ABC=∠ACB可得AB=AC,又点D、E分别是AB、AC的中点.得到AD=AE,通过△ABE≌△ACD,即可得到结果
【小结】本题考查了等腰三角形的性质,全等三角形的判定与性质,熟记定理是解题的关键.
6.(2018?武汉)如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
【分析】求出BF=CE,根据SAS推出△ABF≌△DCE,得对应角相等,由等腰三角形的判定可得结论.
【解答】证明:∵BE=CF,∴BE+EF=CF+EF.∴BF=CE.
在△ABF和△DCE中,∴△ABF≌△DCE(SAS).∴∠GEF=∠GFE.,∴EG=FG.
【小结】本题考查了全等三角形的判定与性质,等腰三角形的判定,熟练掌握三角形全等的判定方法是解题的关键.
7.(2018?泰州)如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
【分析】因为∠A=∠D=90°,AC=BD,BC=BC,知Rt△BAC≌Rt△CDB(HL),所以AB=CD,证明△ABO与△CDO全等,所以有OB=OC.
【小结】此题主要考查了全等三角形的判定,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.
8.(2018?镇江)如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= 75 °.
【分析】(1)要证明△ABE≌△ACF,由题意可得AB=AC,∠B=∠ACF,BE=CF,从而可以证明结论成立;
(2)根据(1)中的结论和等腰三角形的性质可以求得∠ADC的度数.
【小结】本题考查全等三角形的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答
解题模型三
旋转模型
针对训练
9.(2018?柳州)如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
【分析】依据两角及其夹边分别对应相等的两个三角形全等进行判断.
【解答】证明:∵在△ABC和△EDC中,
,
∴△ABC≌△EDC(ASA).
【小结】本题主要考查了全等三角形的判定,两角及其夹边分别对应相等的两个三角形全等.
10.(2018?昆明)如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:BC=DE.
【小结】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.
11.(2017?常州)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
【分析】(1)根据同角的余角相等可得到∠3=∠5,结合条件可得到∠1=∠D,再加上BC=CE,可证得结论;
(2)根据∠ACD=90°,AC=CD,得到∠2=∠D=45°,根据等腰三角形的性质得到∠4=∠6=67.5°,由平角的定义得到∠DEC=180°﹣∠6=112.5°.
【小结】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL
12.(2017?恩施州)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.
【分析】利用“边角边”证明△ACD和△BCE全等,可得可得∠CAE=∠CBD,根据“八字型”证明∠AOP=∠PCB=60°即可.
【小结】本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
解题模型四
平移+旋转模型
针对训练
13.(2018?菏泽)如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.
【分析】结论:DF=AE.只要证明△CDF≌△BAE即可;
【解答】解:结论:DF=AE.
理由:∵AB∥CD,
∴∠C=∠B.
∵CE=BF,
∴CF=BE.
又∵CD=AB,
∴△CDF≌△BAE(SAS).
∴DF=AE.
【小结】本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型
14.(2017?孝感)如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD
【分析】根据全等三角形的判定与性质,可得∠B=∠D,根据平行线的判定,可得答案.
【小结】本题考查了全等三角形的判定与性质,利用等式的性质得出BE=DF是解题关键,又利用了全等三角形的判定与性质.
15.(2018?铜仁)已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥FB.
【分析】可证明△ACE≌△BDF,得出∠A=∠B,即可得出AE∥BF;
【小结】本题考查了全等三角形的判定及性质以及平行线的判定问题,关键是SSS证明△ACE≌△BDF.
16.(2018?怀化)已知:如图,点A,F,E,C在同一直线上,AB∥DC,AB=CD,∠B=∠D.
(1)求证:△ABE≌△CDF;
(2)若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.
【分析】(1)根据平行线的性质得出∠A=∠C,进而利用全等三角形的判定证明即可;
(2)利用全等三角形的性质和中点的性质解答即可.
【解答】证明:(1)∵AB∥DC,∴∠A=∠C.
在△ABE与△CDF中,,∴△ABE≌△CDF(ASA).
(2)∵点E,G分别为线段FC,FD的中点,∴ED=CD.
∵EG=5,∴CD=10.
∵△ABE≌△CDF,∴AB=CD=10.
【小结】此题考查全等三角形的判定和性质,关键是根据平行线的性质得出∠A=∠C.
解题模型五
角平分线模型
针对训练
17.(2016?咸宁)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,
.
求证:
.
请你补全已知和求证,并写出证明过程.
【分析】根据图形写出已知条件和求证,利用全等三角形的判定得出△PDO≌△PEO,由全等三角形的性质可得结论.
【小结】本题主要考查了角平分线的性质和全等三角形的性质及判定,利用图形写出已知条件和求证是解答此题的关键.
解题模型六
三垂直模型
针对训练
18.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.
【分析】先证明∠BCE=∠CAD,再证明△ADC≌△CEB,可得到AD=CE,DC=EB,等量代换,可得出DE=AD+BE.
【小结】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.证明两线段的和等于一条线段常常借助三角形全等来证明,要注意运用这种方法
19.如图,将等腰直角三角形ABC的直角顶点置于直线l上,且过A,B两点分别作直线l的垂线,垂足分别为D,E,请你在图中找出一对全等三角形,并写出证明它们全等的过程.
【分析】分析图可知,全等三角形为:△ACD≌△CBE.根据这两个三角形中的数量关系选择ASA证明全等.
【小结】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
专题三
相似三角形解题模型
解题模型一
A字型
针对训练
1.(2015?湘潭)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
【分析】(1)根据折叠的性质得出∠C=∠AED=90°,利用∠DEB=∠C,∠B=∠B证明三角形相似即可;
(2)由折叠的性质知CD=DE,AC=AE.根据题意在Rt△BDE中运用勾股定理求DE,进而得出AD即可.
【解答】证明:(1)∵∠C=90°,△ACD沿AD折叠,
【小结】本题考查了相似三角形的判定和性质,关键是根据1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、勾股定理求解.
2.(2018?黄石)在△ABC中,E、F分别为线段AB、AC上的点(不与A、B、C重合).
(1)如图1,若EF∥BC,求证:
(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若EF上一点G恰为△ABC的重心,,求的值.
【分析】(1)由EF∥BC知△AEF∽△ABC,据此得=,根据=()2即可得证;
(2)分别过点F、C作AB的垂线,垂足分别为N、H,据此知△AFN∽△ACH,得=,
根据=即可得证;
(3)连接AG并延长交BC于点M,连接BG并延长交AC于点N,连接MN,
由重心性质知S△ABM=S△ACM、=,设=a,
利用(2)中结论知==、==a,
从而得==+a,
结合==a可关于a的方程,解之求得a的值即可得出答案.
∴=.
∴==.
(3)如图2,连接AG并延长交BC于点M,连接BG并延长交AC于点N,连接MN,则MN分别是BC、AC的中点,
【小结】本题主要考查相似形的综合问题,解题的关键是熟练掌握相似三角形的判定与性质和三角形重心的定义及其性质等知识点
3.(2017?衢州)如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接OD.作BE⊥CD于点E,交半圆O于点F.已知CE=12,BE=9.
(1)求证:△COD∽△CBE;
(2)求半圆O的半径r的长.
【分析】(1)由切线的性质和垂直的定义得出∠E=90°=∠CDO,再由∠C=∠C,得出△COD∽△CBE.
(2)由勾股定理求出BC==15,由相似三角形的性质得出比例式,即可得出答案.
【小结】本题考查了切线的性质、相似三角形的判定及其性质、勾股定理;熟练掌握相似三角形的判定与性质是解决问题的关键.
4.(2017?杭州)如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;(2)若AD=3,AB=5,求的值.
【分析】(1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,可证明∠AED=∠ACB,进而可证△ADE∽△ABC;
(2)△ADE∽△ABC,,又易证△EAF∽△CAG,所以,从而可知.
【小结】本题考查相似三角形的判定,解题的关键是熟练运用相似三角形的判定,本题属于中等题型
解题模型二
8字型
针对训练
5.(2018?江西)如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
【分析】根据角平分线定义和平行线的性质求出∠D=∠CBD,求出BC=CD=4,证△AEB∽△CED,得出比例式,求出AE=2CE,即可得出答案.
∴=,∴=,∴AE=2CE
∵AC=6=AE+CE,∴AE=4.
【小结】本题考查了相似三角形的性质和判定和等腰三角形的判定、平行线的性质等知识点,能求出AE=2CE和△ABE∽△CDE是解此题的关键.
6.(2017?来宾)如图,在正方形ABCD中,H为CD的中点,延长AH至F,使AH=3FH,过F作FG⊥CD,垂足为G,过F作BC的垂线交BC的延长线于点E.
(1)求证:△ADH∽△FGH;(2)求证:四边形CEFG是正方形.
【分析】(1)由正方形的性质以及FG⊥CD得出∠ADH=∠FGH=90°,结合对顶角∠AHD=∠FHG,即可判定△ADH∽△FGH;
(2)根据三角形相似的性质得出GF=CG,再根据已知条件FG⊥CD,DC⊥BE,FE⊥BE,即可判定四边形CEFG是正方形.
∴==3.
∵GF=AD,DH=CH,∴CG=2GH,∴CD=6GH.
∴CG=CD.
∴GF=CG.
∵FG⊥CD,DC⊥BE,FE⊥BE,
∴四边形CEFG是正方形.
【小结】本题考查了相似三角形的判定和性质,正方形的判定和性质,熟练掌握性质定理是解题的关键.
解题模型三
母子型
针对训练
7.(2018?东营)如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)求证:∠CAD=∠BDC(2)若BD=AD,AC=3,求CD的长.
求出CD的长.
【解答】(1)证明:连接OD,如图所示
∴CD=2.
【小结】本题考查了相似三角形的判定与性质、圆周角定义以及切线的性质,解题的关键是:(1)利用等角的余角相等证出∠CAD=∠BDC;(2)利用相似三角形的性质找出
解题模型四
一线三等角型
针对训练
8.(2018?杭州)如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD.(2)若AB=13,BC=10,求线段DE的长.
【分析】(1)想办法证明∠B=∠C,∠DEB=∠ADC=90°即可解决问题;
(2)利用面积法:?AD?BD=?AB?DE求解即可;
【小结】本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,学会利用面积法确定线段的长.
9.(2018?盐城节选)如图,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.
(1)若AB=6,AE=4,BD=2,则CF=
;
(2)求证:△EBD∽△DCF.
【分析】(1)先求出BE的长度后发现BE=BD的,又∠B=60°,可知△BDE是等边三角形,可得∠BDE=60°,另外∠DEF=60°,可证得△CDF是等边三角形,从而CF=CD=BC﹣BD;
(2)证明△EBD∽△DCF,这个模型可称为“一线三等角?相似模型”,根据“AA”判定相似.
∴∠CDF+BDE=120°,∠BED+∠BDE=120°.
∴∠BED=∠CDF.
又∠B=∠C=60°,
∴△EBD∽△DCF.
10.(2017?东营)如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
【解答】证明:(1)∵△ABC是等腰三角形,且∠BAC=120°,
∴∠ABD=∠ACB=30°.
∴∠ABD=∠ADE=30°.
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB.
∴△ABD∽△DCE.
(2)如图1,∵AB=AC=2,∠BAC=120°,
(3)当AD=DE时,如图2,
由(1)可知:此时△ABD≌△DCE,则AB=CD,即2=2﹣x,
x=2﹣2,代入y=x+2,
解得y=4﹣2,即AE=4﹣2.
当AE=ED时,如图3,∠EAD=∠EDA=30°,∠AED=120°,
∴∠DEC=60°,∠EDC=90°,
则ED=EC,即y=(2﹣y).解得y=,即AE=.
当AD=AE时,∠AED=∠EDA=30°,∠EAD=120°,
此时点D与点B重合,不符合题意,此情况不存在,
∴当△ADE是等腰三角形时,AE=4﹣2或.
【小结】本题是相似形的综合题,考查了三角形相似的性质和判定、等腰三角形的性质、直角三角形30°角的性质,本题的几个问题全部围绕△ABD∽△DCE,解决问题;难度适中.
解题模型五
一线三垂直型
针对训练
11.(2018?梧州)如图,AB是⊙M的直径,BC是⊙M的切线,切点为B,C是BC上(除B点外)的任意一点,连接CM交⊙M于点G,过点C作DC⊥BC交BG的延长线于点D,连接AG并延长交BC于点E.
(1)求证:△ABE∽△BCD;
(2)若MB=BE=1,求CD的长度.
【分析】(1)根据直径所对圆周角和切线性质,证明三角形相似;
(2)利用勾股定理和面积法得到AG、GE,根据三角形相似求得GH,得到MB、GH和CD的数量关系,求得CD.
【解答】(1)证明:∵BC为⊙M切线
∴∠ABC=90°.
∵DC⊥BC,
∴∠BCD=90°.
∴∠ABC=∠BCD.
∵AB是⊙M的直径,
∴∠AGB=90°,即BG⊥AE.
∴∠CBD=∠A.
∴△ABE∽△BCD.
(2)解:过点G作GH⊥BC于点H.
∴GH=.
又∵GH∥AB,
【小结】本题是几何综合题,综合考察了圆周角定理、切线性质和三角形相似.解答时,注意根据条件构造相似三角形.
12.(2018?武汉)在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,,直接写出tan∠CEB的值.
【分析】(1)利用同角的余角相等判断出∠BAM=∠CBN,即可得出结论;
(2)先判断出MP=MC,进而得出=,设MN=2m,PN=m,
根据勾股定理得,PM==3m=CM,即可得出结论;
(3)先判断出=,再同(2)的方法,即可得出结论.
【解答】解:(1)∵AM⊥MN,CN⊥MN,
∴∠AMB=∠BNC=90°.
∴∠BAM+∠ABM=90°.
∵∠ABC=90°,
(3)在Rt△ABC中,sin∠BAC==,
如图3,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于点H.
∵∠DEB=90°,∴CH∥AG∥DE,∴=.
同(1)的方法得,△ABG∽△BCH,∴.
设BG=4m,CH=3m,AG=4n,BH=3n,
∵AB=AE,AG⊥BE,∴EG=BG=4m.
【小结】此题是相似形综合题,主要考查了同角的余角相等,相似三角形的判定和性质,锐角三角函数,平行线分线段成比例定理,构造图1是解本题的关键.
专题四
三角函数应用解题模型
解题模型一
“独立”型
图形
关系式
针对训练
1.(2018?台州)图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
【小结】本题考查了解直角三角形的应用:先将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题),然后利用勾股定理和三角函数的定义进行几何计算
解题模型二
“背靠背”型
图形
关系式
针对训练
2.(2018?临沂)如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2(+1)m.请计算说明,工人师傅搬运此钢架能否通过一个直径为2.1m的圆形门?
【小结】本题考查了解直角三角形的应用,解一元一次方程等知识点,能正确求出BD的长是解此题的关键.
3.(2018?长沙)为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)
(2)∵cos30°=,BC=80(千米),∴BD=BC?cos30°=80×(千米).
∵tan45°=,CD=40(千米),∴AD=(千米).
∴AB=AD+BD=40+40≈40+40×1.73=109.2(千米).
∴汽车从A地到B地比原来少走多少路程为:AC+BC﹣AB=136.4﹣109.2=27.2(千米).
【小结】本题考查了勾股定理的运用以及解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
4.(2018?陇南)随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:≈1.7,≈1.4)
答:隧道打通后与打通前相比,从A地到B地的路程将约缩短224公里.
【小结】本题考查的是解直角三角形的应用﹣方向角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,需要熟记锐角三角函数的定义.
5.(2018?常州)京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
【小结】此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.
6.(2017?岳阳)某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.
(1)求支架CD的长;
(2)求真空热水管AB的长.(结果保留根号)
【小结】此题主要考查了解直角三角形的应用,要熟练掌握,注意将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
7.(2017?赤峰)王浩同学用木板制作一个带有卡槽的三角形手机架,如图所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
【解析】根据题意作出合适的辅助线,可以求得AD和CD的长,进而可以求得DB的长,然后根据勾股定理即可得到AB的长,然后与17比较大小,即可解答本题.
【小结】本题考查解直角三角形的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用直角三角形的相关知识解答
解题模型三
“母抱子”型
图形
关系式
针对训练
8.(2017?白银)美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
【小结】本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型
9.(2017?宜宾)如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A,又在河的另一岸边取两点B、C测得∠α=30°,∠β=45°,量得BC长为100米.求河的宽度(结果保留根号).
【小结】此题主要考查了解直角三角形的应用,正确得出AD=CD是解题关键.
10.(2016?青海)如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)求办公楼AB的高度;(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈,cos22°,tan22)
【小结】此题主要考查了解直角三角形的应用,根据已知得出tan22°=是解题关键.
11.(2016?六盘水)据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
【解析】(1)在直角三角形ABD与直角三角形ACD中,利用锐角三角函数定义求出BD与CD的长,由BD﹣CD求出BC的长即可;
(2)根据路程除以时间求出该轿车的速度,即可作出判断.
解:(1)在Rt△ABD中,AD=24m,∠B=31°,
∴tan31°=,即BD==40m.
在Rt△ACD中,AD=24m,∠ACD=50°,
∴tan50°=,即CD==20m.
∴BC=BD﹣CD=40﹣20=20m.
则BC的距离为20m.
(2)根据题意,得20÷2=10m/s<15m/s,
则此轿车没有超速.
【小结】此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.
12.(2016?兰州)如图,一垂直于地面的灯柱AB被一钢线CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
【小结】本题考查解直角三角形的应用,解题的关键是明确题意,利用三角函数值求出相应的边的长度.
13.(2017?张家界)位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
【小结】此题主要考查了解直角三角形的应用,正确掌握锐角三角函数关系是解题关键
14.(2017?呼和浩特)如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(结果用含非特殊角的三角函数和根式表示即可)
【解析】过点C作CM⊥AB交AB延长线于点M,通过解直角△ACM得到AM的长度,通过解直角△BCM得到BM的长度,则AB=AM﹣BM.
【小结】本题考查解直角三角形的应用、三角函数等知识,解题的关键是添加辅助线,构造直角三角形,记住三角函数的定义,以及特殊三角形的边角关系,属于中考常考题型.
15.(2018?烟台)汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
【解析】先求得AC=PCtan∠APC=87、BC=PCtan∠BPC=21,据此得出AB=AC﹣BC=87﹣21=66,从而求得该车通过AB段的车速,比较大小即可得.
解:在Rt△APC中,AC=PCtan∠APC=30tan71°≈30×2.90=87,
在Rt△BPC中,BC=PCtan∠BPC=30tan35°≈30×0.70=21,
则AB=AC﹣BC=87﹣21=66,
∴该汽车的实际速度为=11m/s.
又∵40km/h≈11.1m/s,
∴该车没有超速.
【小结】此题考查了解直角三角形的应用,涉及的知识有:锐角三角函数定义,熟练掌握三角函数的定义是解本题的关键.
16.(2017?铁岭)如图,某市文化节期间,在景观湖中央搭建了一个舞台C,在岸边搭建了三个看台A,B,D,其中A,C,D三点在同一条直线上,看台A,B到舞台C的距离相等,测得∠A=30°,∠D=45°,AB=60m,小明、小丽分别在B,D看台观看演出,请分别求出小明、小丽与舞台C的距离.(结果保留根号)
【解析】如图作BH⊥AD于H.,CE⊥AB于E.解直角三角形,分别求出BC、CD即可解决问题.
解:如图,作BH⊥AD于点H,CE⊥AB于点E.
∴BH=DH=30.
∴DC=DH+CH=30+10.
答:小明、小丽与舞台C的距离分别为20m和(30+10)m.
【小结】本题考查解直角三角形、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
17.(2017?广元)如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).
【小结】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用特殊角的三角函数值解答.
18.(2017?贵阳)贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
【小结】本题考查了解直角三角形的应用,首先构造直角三角形,再运用三角函数的定义解题,构造出直角三角形是解题的关键.
19.(2017?西宁)如图,建设“幸福西宁”,打造“绿色发展样板城市”.美丽的湟水河宛如一条玉带穿城而过,已形成“水清、流畅、岸绿、景美”的生态环境新格局.在数学课外实践活动中,小亮在海湖新区自行车绿道北段AC上的A,B两点分别对南岸的体育中心D进行测量,分别测得∠DAC=30°,∠DBC=60°,AB=200米,求体育中心D到湟水河北岸AC的距离约为多少米(精确到1米,≈1.732)?
【小结】本题考查了解直角三角形的应用.主要是正切概念及运算,关键把实际问题转化为数学问题加以计算
解题模型四
“斜截”型
图示:辅助线作法——延长四边形对边法
针对训练
20.(2016?娄底)芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)
解得x=10﹣,∴BH=2+(10﹣)=10﹣1≈16.3(米).答:立柱BH的长约为16.3米.
【小结】本题考查了解直角三角形的应用;由三角函数求出CH和AH是解决问题的关键.
21.(2018?随州)随州市新?水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;(2)求最长的斜拉索AC的长.
∴AB=3BD=5×3=15.
在Rt△ABH中,∵∠B=45°,
∴BH=AH=AB=×15=15.
在Rt△ACH中,∵∠C=30°,
∴AC=2AH=30.
答:最长的斜拉索AC的长为30m.
【小结】本题考查了解直角三角形的应用:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
22.(2017?凉山州)如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
【解析】延长OC,AB交于点P,△PCB∽△PAO,根据相似三角形对应边比例相等的性质即可解题.
解:如图,延长OC,AB交于点P.
∵∠ABC=120°,
∴∠PBC=60°.
【小结】本题考查了通过作辅助线构建直角三角形的能力,考查了相似三角形的判定和性质,本题中求证△PCB∽△PAO是解题的关键.
解题模型五
其他类型
23.(2018?徐州)如图,1号楼在2号楼的南侧,两楼高度均为90m,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=42m.
(1)求楼间距AB;
(2)若2号楼共30层,层高均为3m,则点C位于第几层?(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
【解析】(1)构造出两个直角三角形,利用两个角的正切值即可求出答案.
24.(2018?资阳)如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米.
(1)当风筝的水平距离AC=18米时,求此时风筝线AD的长度;
(2)当她从点A跑动9米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
答:此时风筝线AD的长度为12米.
方法二:设CD=x,
∵∠CAD=30°,
∴BE=AD=2CD=2x,AC===x.
∵CF=10,
∴AF=AC﹣CF=x﹣10.
∵AB=9,
∴BF=AB+AF=9+x﹣10.
∵∠EBF=45°,
∴由cos∠EBF=可得=.
解得x=12+,即CD=12+,
则C1D=CD+C1C=12++=+.
答:风筝原来的高度C1D为(+)米.
【小结】本题主要考查解直角三角形的应用,解题的关键是掌握三角函数的定义及根据题意找到两直角三角形间的关联.
25.(2018?常德)图1是一商场的推拉门,已知门的宽度AD=2米,且两扇门的大小相同(即AB=CD),将左边的门ABB1A1绕门轴AA1向里面旋转37°,将右边的门CDD1C1绕门轴DD1向外面旋转45°,其示意图如图2,求此时B与C之间的距离(结果保留一位小数).(参考数据:sin37°≈0.6,cos37°≈0.8,≈1.4)
∴BE∥CM.
又∵BE=CM,
∴四边形BEMC为平行四边形.
∴BC=EM,CM=BE.
在Rt△MEF中,EF=AD﹣AE﹣DF=0.5,FM=CF+CM=1.3,
∴EM=≈1.4.
∴B与C之间的距离约为1.4米.
【小结】本题考查了解直角三角形的应用、勾股定理以及平行四边形的判定与性质,构造直角三角形,利用勾股定理求出BC的长度是解题的关键.
26.(2018?岳阳)图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:≈1.73,结果精确到0.01米)
∴ON=OM=0.6,∴NB=ON+OB=3.3+0.6=3.9,即点M到地面的距离是3.9米
【小结】本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会添加常用辅助线,在直角三角形解决问题,属于中考常考题型.
27.(2017?桂林)“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
【解析】在Rt△BED中可先求得BE的长,过点C作CF⊥AE于点F,则可求得AF的长,从而可求得EF的长,即可求得CD的长.
解:∵BN∥ED,
【小结】本题主要考查解直角三角形的应用,利用条件构造直角三角形是解题的关键,注意角度的应用.
28.(2017?常德)如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,≈1.732,≈1.414)
【小结】本题考查解直角三角形、锐角三角函数、解题的关键是添加辅助线,构造直角三角形,记住锐角三角函数的定义,属于中考常考题型。
专题五
反比例函数K的几何意义解题模型
解题模型一
图形
关系式
S阴影=|k|
针对训练
1.(2018?毕节)已知点P(﹣3,2),点Q(2,a)都在反比例函数y=(k≠0)的图象上,过点Q分别作两坐标轴的垂线,两垂线与两坐标轴围成的矩形面积为( )
A.3
B.6
C.9
D.12
【小结】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
2.(2017?阜新)在平面直角坐标系中,点P是反比例函数y=(x<0)图象上的一点,分别过点P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为6,则k的值是
【小结】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
3.(2018?相山区三模)如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为4,则这个反比例函数的解析式为
.
【解析】过A点向x轴作垂线,与坐标轴围成的四边形的面积是定值|k|,由此可得出答案.
解:过A点向x轴作垂线,如图:
根据反比例函数的几何意义可得:四边形ABCD的面积为4,即|k|=4,
又∵函数图象在二、四象限,∴k=﹣4,即函数解析式为:y=﹣.
【点评】本题考查了反比例函数的几何意义,解答本题关键是掌握在反比例函数中k所代表的几何意义,属于基础题,难度一般.
解题模型二
图形
关系式
S阴影=
针对训练
4.(2017?铜仁)如图,已知点A在反比例函数y=上,AC⊥x轴,垂足为点C,且△AOC的面积为4,则此反比例函数的表达式为( )
A.y=
B.y=
C.y=
D.y=﹣
【解析】由S△AOC=xy=4,设反比例函数的解析式y=,则k=xy=8
解:∵S△AOC=4,
∴k=2S△AOC=8;
∴y=;
故选:C.
【小结】此题考查了待定系数法求反比例函数解析式,反比例函数系数k的几何意义.属于基础题,难度不大
5.(2018?苏州)如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=,则k的值为( )
A.3
B.2
C.6
D.12
∴k=12a2=(4+4a)a,
解得:a=或a=0(舍),
则k=12×=3,
故选:A.
【小结】本题主要考查反比例函数图象上点的坐标特征,解题的关键是根据题意表示出点D、E的坐标及反比例函数图象上点的横纵坐标乘积都等于反比例系数k.
6.(2018?娄底)如图,在平面直角坐标系中,O为坐标原点,点P是反比例函数y=图象上的一点,PA⊥x轴于点A,则△POA的面积为
.
【小结】此题主要考查了反比例函数系数k的几何意义,正确表示出△POA的面积是解题关键.
7.(2017?永州)如图,已知反比例函数y=(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=
.
【解析】根据反比例函数的性质可以得到△AOB的面积等于|k|的一半,由此可以得到它们的关系.
解:依据比例系数k的几何意义可得两个三角形的面积都等于|k|=1,解得k=﹣2,
故答案为:﹣2.
【小结】本题考查反比例系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.
8.(2018?衢州)如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=
.
【小结】此题考查了反比例函数系数k的几何意义,以及反比例函数图象上点的坐标特征,熟练掌握反比例函数k的几何意义是解本题的关键
解题模型三
图形
关系式
S△ABC=|k|
S△APP1=2|k|
针对训练
9.(2018?江干区一模)下列与反比例函数图象有关图形中,阴影部分面积最小的是( )
A.
B.
C.
D.
【点评】本题考查反比例函数系数k的几何意义,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
10.(2018?凤城市模拟)如图,A,B是函数y=图象上关于原点对称的两点,BC∥x轴,AC∥y轴,若△ABC的面积为8,则k的值是
.
【点评】本题考查的是反比例函数的性质,熟知反比例函数系数k的几何意义是解答此题的关键.
解题模型四
图形
关系式
针对训练
11.(2018?郴州)如图,A,B是反比例函数y=在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是(
【点评】本题考查了反比例函数中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.也考查了反比例函数图象上点的坐标特征,梯形的面积.
12.(2018?铜梁区模拟)如图,已知A、B两点是反比例函数y=(x>0)的图象上任意两点,过A、B两点分别作y轴的垂线,垂足分别为C、D,连接AB、AO、BO,则四边形ABDC的面积与△AOB的面积之比值( )
A.等于1
B.小于1
C.大于1
D.不确定
【点评】本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|
解题模型五
图形
关系式
S阴影=
S阴影=
针对训练
13.(2018?徐州)如图,在平面直角坐标系中,函数y=kx与y=﹣的图象交于A,B两点,过A作y轴的垂线,交函数y=的图象于点C,连接BC,则△ABC的面积为( )
A.2
B.4
C.6
D.8
∴S△ABC=×(﹣2x﹣x)?(﹣﹣)=×(﹣3x)?(﹣)=6.
故选:C.
【小结】本题考查了反比例函数与正比例函数图象的特点,垂直于y轴的直线上任意两点的坐标特点,三角形的面积,解答此题的关键是找出A、B两点与A、C两点坐标的关系.
14.(2018?贵阳)如图,过x轴上任意一点P作y轴的平行线,分别与反比例函数y=(x>0),y=﹣(x>0)的图象交于A点和B点,若C为y轴任意一点.连接AC、BC,则△ABC的面积为
.
【小结】本题考查反比例函数中比例系数k的几何意义,本题也可直接套用结论求解.
15.(2018?黑龙江)如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=(x>0)、y=(x<0)的图象于B、C两点,若△ABC的面积为2,则k值为( )
A.﹣1
B.1
C.
D.
【小结】本题考查了反比例函数系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.
解题模型六
图示:
针对训练
16.(2018?宁波)如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为( )
A.8
B.﹣8
C.4
D.﹣4
【小结】本题考查了反比例函数图象上点的坐标特征,点在函数的图象上,则点的坐标满足函数的解析式.也考查了三角形的面积.
17.(2018?唐河县三模)如图,设点P在函数y=的图象上,PC⊥x轴于点C,交函数y=的图象于点A,PD⊥y轴于点D,交函数y=的图象于点B,则四边形PAOB的面积为 4 .
【小结】本题考查了比例系数k的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|
专题六线段最值问题解题模型
解决几何最值问题的理论依据有:①两点之间线段最短;②垂线段最短;③三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值);④定圆中的所有弦中,直径最长;⑤圆外一点与圆心的连线上,该点和此直线与圆的近交点距离最短、远交点距离最长.根据不同特征转化从而减少变量是解决最值问题的关键,直接套用基本模型是解决几何最值问题的高效手段.
解题模型一
图形
转化
直线l外有一定点A,点B是直线l上的一个动点,求AB的最小值.
过定点A作AB⊥l于点B.
针对训练
1.(2018?长春)如图,在?ABCD中,AD=7,AB=2,∠B=60°.E是边BC上任意一点,沿AE剪开,将△ABE沿BC方向平移到△DCF的位置,得到四边形AEFD,则四边形AEFD周长的最小值为 20 .
【小结】此题考查平移的性质,关键是根据当AE⊥BC时,四边形AEFD的周长最小进行分析
解题模型二
图形
转化
A,B为定点,l为定直线,P为直线l上的一个动点,求AP+BP的最小值.
作其中一个定点关于定直线l的对称点,连接对称点与另一定点.
点A是l上的动点,B,P是定点,求PA+AB最小值.
作点P关于直线l1的对称点P’,则P’B为PA+AB的最小值.
针对训练
2.(2018?天津)如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的
【小结】本题考查的是轴对称,最短路线问题,根据题意作出A关于BD的对称点C是解答此题的关键.
3.(2018?十堰)如图,Rt△ABC中,∠BAC=90°,AB=3,AC=6,点D,E分别是边BC,AC上的动点,则DA+DE的最小值为
.
∵∠A'FD=∠DEC=90°,∠A'DF=∠CDE,
∴∠A'=∠C,
∵∠AEA'=∠BAC=90°,
∴△AEA'∽△BAC,
∴,
∴,
∴A'E=,
即AD+DE的最小值是;
【小结】本题考查轴对称﹣最短问题、三角形相似的性质和判定、两点之间线段最短、垂线段最短等知识,解题的关键是灵活运用轴对称以及垂线段最短解决最短问题,属于中考填空题中的压轴题.
解题模型三
图形
转化
P为定点,M,N为定直线上的动点,求△PMN周长的最小值.
过定点P分别作关于两条定直线的对称点,连接两对称点.
求直线l1,l2上的点M,N,使得四边形PQMN的周长最小.
作定点Q关于直线l1的对称点Q’,作定点P关于直线l2的对称点P’,连接Q’P’,分别交直线l1,l2于点M,N
针对训练
4.(2015?营口)如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数
∵△PMN周长的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°;
【小结】本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质;熟练掌握轴对称的性质,证明三角形是等边三角形是解决问题的关键.
5.(2015?玉林)如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
∵AD=A′D=3,BE=BE′=1,∴AA′=6,AE′=4.
∵DQ∥AE′,D是AA′的中点,∴DQ是△AA′E′的中位线,
【小结】本题考查了轴对称,利用轴对称确定A′、E′,连接A′E′得出P、Q的位置是解题关键,又利用了相似三角形的判定与性质,图形分割法是求面积的重要方法.
解题模型四
图形
转化
直线m∥n,在m,n上分别求点M,N,使MN⊥m,且AM+MN+BN的值最小
将点A向下平移MN的单位长度得A′,连接A′B,交n于点N,过点N作MN⊥m于M,点M,N即为所求.
在直线l上求两点M,N(M在左),使MN=a,并使AM+MN+NB的值最小.
将点A向右平移a个长度单位得A′,作A′关于l的对称点A″,连接A″B,交直线l于点N,将N点向左平移a个单位长度得M.
针对训练
6.(2017?内江)如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=
.
【小结】本题考查轴对称﹣最短问题、平行线的性质、平行四边形的判定和性质、勾股定理等知识,解题的关键是学会构建平行四边形解决问题,属于中考常考题型
解题模型五
图形
转化
P是圆上一动点,求AP的最大值和最小值.
当P点运动到点B时,AP取得最小值;当P点运动到点C时,AP取得最大值.
P为圆内一定点,求过点P的弦的最小值与最大值.
AB是过圆O内定点P的弦.当OP⊥AB时,过点P的弦的最小值为线段AB;过点P的弦的最大值为圆的直径.
针对训练
7.(2015?自贡)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A.2﹣2
B.6
C.2﹣2
D.4
∴AE=EB′=2,
∵AD=6,
∴DE==2,
∴DB′=2﹣2.
故选:A.
【小结】本题主要考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用,确定点B′在何位置时,B′D的值最小,是解决问题的关键.
8.(2018?内江)如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O的半径r=2,直线AB不垂直于直线l,过点A,B分别作直线l的垂线,垂足分别为点D,C,则四边形ABCD的面积的最大值为 12 .
【小结】本题考查了梯形中位线:梯形的中位线平行于两底,并且等于两底和的一半.
解题模型六
图例[]
圆柱
则AB2=B′A2+B′B2
长
方
体
阶梯
问题
基本
思路
将立体图形展开成平面图形→利用两点之间线段最短确定最短路线→构造直角三角形→利用勾股定理求解
针对训练
9.(2018?黄冈)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 20 cm(杯壁厚度不计).
【解析】将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解:如图:将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B===20(cm).故答案为20.
【小结】本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
10.(2017?东营)我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 25 尺.
【小结】本题考查了平面展开最短路径问题,关键是把立体图形展成平面图形,本题是展成平面图形后为直角三角形按照勾股定理可求出解.
专题七
等腰三角形综合题解题模型
解题模型一
等边三角形共顶点
等边△ABC与等边△DCE,B、C、E三点共线.
连接BD、AE交于点F,BD交AC于点G,AE交DC于点H,连接CF、GH,则:
(1)△BCD≌△ACE;
(2)AE=BD;
(3)∠AFB=∠DFE=60°;
(4)FC平分∠BFE;
(5)BF=AF+FC,EF=DF+FC;
(6)△CGH为等边三角形.
针对训练
1.(2017?恩施)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.
【答案】证明:∵△ABC和△ECD都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°.
∴∠ACB+∠BCE=∠DCE+∠BCE,即∠ACE=∠BCD.
在△ACE和△BCD中,,
∴△ACE≌△BCD(SAS).
∴∠CAE=∠CBD.
∵∠APC=∠BPO,
∴∠BOP=∠ACP=60°,即∠AOB=60°.
【小结】本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
解题模型二
等腰直角三角形共顶点
等腰Rt△ABC与等腰Rt△DCE中,∠ACB=∠DCE=90°.
如图1,连接BD、AE交于点F,连接FC、AD、BE,则:
(1)△BCD≌△ACE;
(2)AE=BD;
(3)AE⊥BD;
(4)FC平分∠BFE;
(5)AB2+DE2=AD2+BE2
(6)BF=AF+FC,EF=DF+FC;
(7)如图2,若G、I分别为BE、AD的中点,则GC⊥AD、IC⊥BE(反之亦然);
(8)S△ACD=S△BCE.
针对训练
2.(2018?东营)如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )
A.①②③④
B.②④
C.①②③
D.①③④
【小结】本题考查全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考选择题中的压轴题.
3.(2017?哈尔滨)已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.
(1)如图1,求证:AE=BD;[]
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
【解析】(1)∵△ACB和△DCE都是等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,DC=EC.
∴∠ACB+∠ACD=∠DCE+∠ACD.
∴∠BCD=∠ACE.
在△ACE与△BCD中,
∴△ACE≌△BCD(SAS).
∴AE=BD.
(2)由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC,
∴∠DOM=90°.
∵∠AEC=∠CAE=∠CBD,
∴△EMC≌△BCN(ASA).
∴CM=CN,
∴DM=AN.
∴△AON≌△DOM(AAS).
∵DE=AB,AO=DO,
∴△AOB≌△DOE(HL).
【小结】本题考查全等三角形,解题的关键是熟练运用全等三角形的判定条件,本题属于基础题型.
解题模型三
等腰三角形共顶点
等腰△ACB与等腰△DCE中,AC=BC,DC=CE,且∠ACB=∠DCE.
连接BD,AE交于点F,则:
(1)△BCD≌△ACE;
(2)AE=BD;
(3)∠AFB=∠ACB;
(4)FC平分∠BFE.
针对训练
4.(2018?河南)(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①的值为 1 ;②∠AMB的度数为 40° .
(2)类比探究:如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由;
(3)拓展延伸:在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=,请直接写出当点C与点M重合时AC的长.
(3)正确画图形,当点C与点M重合时,有两种情况:如图3和4,同理可得:△AOC∽△BOD,则∠AMB=90°,,可得AC的长.
故答案为:①1;②40°.
(2)类比探究
如图2,=,∠AMB=90°,理由是:Rt△COD中,∠DCO=30°,∠DOC=90°,∴.
同理得:,∴.
∵∠AOB=∠COD=90°,∴∠AOC=∠BOD,∴△AOC∽△BOD.[]∴=,∠CAO=∠DBO.
在△AMB中,∠AMB=180°﹣(∠MAB+∠ABM)=180°﹣(∠OAB+∠ABM+∠DBO)=90°.
(3)拓展延伸
【小结】本题是三角形的综合题,主要考查了三角形全等和相似的性质和判定,几何变换问题,解题的关键是能得出:△AOC∽△BOD,根据相似三角形的性质,并运用类比的思想解决问题,本题是一道比较好的题目.
角平分线相关问题模型
解题模型一
针对训练
1.(2016?枣庄)如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
A.15°
B.17.5°
C.20°
D.22.5°
【小结】本题若不套用模型,则需要通过三角形的外角性质证明得到∠A、∠D的数量关系.
2.(2018?巴中)如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=
.
【分析】由解题模型一中的(1)可知,∠BOC=90°+∠A,把∠BOC=110°代入计算可得到∠A的度数.
【详解】∵∠BOC=90°+∠A,∠BOC=110°,∴90°+∠A=110°.∴∠A=40°.
【小结】本题若不套用模型,需要利用三角形的内角和定理、角平分线的定义得到∠BOC、∠A的数量关系.
3.(2018?深圳)在Rt△ABC中,∠C=90°,AD平分∠CAB,BE平分∠ABC,AD、BE相交于点F,且AF=4,EF=,则AC= .
∵AD平分∠CAB,BE平分∠ABC,∴CF是∠ACB的平分线.∴∠ACF=45°=∠AFE.
∵∠CAF=∠FAE,∴△AEF∽△AFC.∴.∴AC===,故答案为.
【小结】此题主要考查了角平分线定义,勾股定理,相似三角形的判定和性质,求出AE是解本题的关键.
4.(2018?济南历城区模拟)如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2018=
.
【详解】∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
【小结】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义,熟记性质然后推出后一个角是前一个角的一半是解题的关键。
解题模型二
针对训练
5.(2018?长春)如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为( )
A.44°
B.40°
C.39°
D.38°
【小结】此题考查三角形内角和问题,关键是根据三角形内角和、角平分线的定义和平行线的性质详解.
6.(2016?湖州)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8
B.6
C.4
D.2
【分析】过点P作PE⊥BC于E,根据角平分线上的点到角的两边的距离相等可得PA=PE,PD=PE,那么PE=PA=PD,又AD=8,进而求出PE=4
【详解】过点P作PE⊥BC于点E.
∵AB∥CD,PA⊥AB,∴PD⊥CD.
∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE.,∴PE=PA=PD.
∵PA+PD=AD=8,∴PA=PD=4.∴PE=4.故选:C.
【小结】本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并作辅助线是解题的关键.
7.(2018?常德)如图,已知BD是△ABC的角平分线,ED是BC的垂直平分线,∠BAC=90°,AD=3,则CE的长为( )
A.6
B.5
C.4
D.3
【小结】本题考查的是线段垂直平分线的性质、直角三角形的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.
8.(2018?淄博)如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
A.4
B.6
C.
D.8
【分析】根据题意,可以求得∠B的度数,然后根据解直角三角形的知识可以求得NC的长,从而可以求得BC的长.
【小结】本题考查30°角的直角三角形、平行线的性质、等腰三角形的判定与性质,详解本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想详解.
9.(2018?大庆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30°
B.35°
C.45°
D.60°
【分析】作MN⊥AD于N,根据平行线的性质求出∠DAB,根据角平分线的判定定理得到∠MAB=∠DAB,计算即可
【小结】本题考查的是角平分线的判定和性质,掌握角的平分线上的点到角的两个端点的距离相等.
10.(2018?河北)如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
A.4.5
B.4
C.3
D.2
【分析】连接AI、BI,因为三角形的内心是角平分线的交点,所以AI是∠CAB的平分线,由平行的性质和等角对等边可得:AD=DI,同理BE=EI,所以图中阴影部分的周长就是边AB的长.
【小结】本题考查了三角形内心的定义、平移的性质及角平分线的定义等知识,熟练掌握三角形的内心是角平分线的交点是关键.
11.(2018?枣庄)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A.
B.
C.
D.
【分析】根据三角形的内角和定理得出∠CAF+∠CFA=90°,∠FAD+∠AED=90°,根据角平分线和对顶角相等得出∠CEF=∠CFE,即可得出EC=FC,再利用相似三角形的判定与性质得出答案.
【详解】过点F作FG⊥AB于点G,如图所示.
∴BC=4,∴=
∵FC=FG,∴=,解得FC=,
即CE的长为.故选:A.
【小结】本题考查了直角三角形性质、等腰三角形的性质和判定,三角形的内角和定理以及相似三角形的判定与性质等知识,关键是推出∠CEF=∠CFE.
12.(2017?滨州)如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )
A.4
B.3
C.2
D.1
在△POE和△POF中,,∴△POE≌△POF(HL).∴OE=OF.
在△PEM和△PFN中,,∴△PEM≌△PFN(ASA).∴EM=NF,PM=PN,故(1)正确.
∴S△PEM=S△PNF,∴S四边形PMON=S四边形PEOF=定值,故(3)正确.∵OM+ON=OE+ME+OF﹣NF=2OE=定值,故(2)正确,MN的长度是变化的,故(4)错误.,故选:B.
【小结】本题考查全等三角形的性质、角平分线的性质定理、四边形的面积等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
13.(2018?德州)如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为 3 .
【小结】此题主要考查了角平分线的性质,关键是掌握角的平分线上的点到角的两边的距离相等.
14.(2018?广安)如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF= 2 .
【分析】作EH⊥OA于点H,根据角平分线的性质求出EH,根据直角三角形的性质求出EF,根据等腰三角形的性质详解.
【详解】作EH⊥OA于点H,如图所示.
【小结】本题考查的是角平分线的性质、平行线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
15.(2018?桂林)如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是 3 .
【答案】3
【分析】首先根据已知条件分别计算图中每一个三角形每个角的度数,然后根据等腰三角形的判定:等角对等边详解,做题时要注意,从最明显的找起,由易到难,不重不漏
【小结】本题考查了等腰三角形的性质及等腰三角形的判定,角的平分线的性质;求得各个角的度数是正确详解本题的关键.
16.(2016?长春)感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)
【分析】探究:欲证明DB=DC,只要证明△DFC≌△DEB即可.
应用:先证明△DFC≌△DEB,再证明△ADF≌△ADE,结合BD=EB即可解决问题.
【详解】探究:证明:如图②中,DE⊥AB于E,DF⊥AC于F,]
∵DA平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD.
在△DFC和△DEB中,,∴△DFC≌△DEB(AAS).∴DC=DB.
∴AB﹣AC=a.故答案为a.
【小结】本题考查全等三角形的判定和性质、角平分线的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.
专题二
全等三角形解题模型
解题模型一
平移模型
针对训练
1.(2018?桂林)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
【分析】(1)求出AC=DF,根据SSS推出△ABC≌△DEF.
(2)由(1)中全等三角形的性质得到:∠A=∠EDF,进而得出结论即可.
【小结】本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应角相等.
解题模型二
对称模型
针对训练
2.(2018?南充)如图,已知AB=AD,AC=AE,∠BAE=∠DAC.
求证:∠C=∠E.
【分析】由∠BAE=∠DAC可得到∠BAC=∠DAE,再根据“SAS”可判断△BAC≌△DAE,根据全等的性质即可得到∠C=∠E.
【小结】本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应角相等,对应边相等.
3.(2018?广州)如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.
【分析】根据AE=EC,DE=BE,∠AED和∠CEB是对顶角,利用SAS证明△ADE≌△CBE即可.
【解答】证明:在△AED和△CEB中,
,
∴△AED≌△CEB(SAS).
∴∠A=∠C(全等三角形对应角相等).
【小结】此题主要考查学生对全等三角形的判定与性质这一知识点的理解和掌握,此题难度不大,要求学生应熟练掌握.
4.(2018?乐山)如图,已知∠1=∠2,∠3=∠4,求证:BC=BD.
【分析】由∠3=∠4可以得出∠ABD=∠ABC,再利用ASA就可以得出△ADB≌△ACB,就可以得出结论.
【小结】本题考查了等角的补角相等的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.
5.(2017?郴州)已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.
【分析】由∠ABC=∠ACB可得AB=AC,又点D、E分别是AB、AC的中点.得到AD=AE,通过△ABE≌△ACD,即可得到结果
【小结】本题考查了等腰三角形的性质,全等三角形的判定与性质,熟记定理是解题的关键.
6.(2018?武汉)如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
【分析】求出BF=CE,根据SAS推出△ABF≌△DCE,得对应角相等,由等腰三角形的判定可得结论.
【解答】证明:∵BE=CF,∴BE+EF=CF+EF.∴BF=CE.
在△ABF和△DCE中,∴△ABF≌△DCE(SAS).∴∠GEF=∠GFE.,∴EG=FG.
【小结】本题考查了全等三角形的判定与性质,等腰三角形的判定,熟练掌握三角形全等的判定方法是解题的关键.
7.(2018?泰州)如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
【分析】因为∠A=∠D=90°,AC=BD,BC=BC,知Rt△BAC≌Rt△CDB(HL),所以AB=CD,证明△ABO与△CDO全等,所以有OB=OC.
【小结】此题主要考查了全等三角形的判定,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.
8.(2018?镇江)如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= 75 °.
【分析】(1)要证明△ABE≌△ACF,由题意可得AB=AC,∠B=∠ACF,BE=CF,从而可以证明结论成立;
(2)根据(1)中的结论和等腰三角形的性质可以求得∠ADC的度数.
【小结】本题考查全等三角形的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答
解题模型三
旋转模型
针对训练
9.(2018?柳州)如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
【分析】依据两角及其夹边分别对应相等的两个三角形全等进行判断.
【解答】证明:∵在△ABC和△EDC中,
,
∴△ABC≌△EDC(ASA).
【小结】本题主要考查了全等三角形的判定,两角及其夹边分别对应相等的两个三角形全等.
10.(2018?昆明)如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:BC=DE.
【小结】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.
11.(2017?常州)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
【分析】(1)根据同角的余角相等可得到∠3=∠5,结合条件可得到∠1=∠D,再加上BC=CE,可证得结论;
(2)根据∠ACD=90°,AC=CD,得到∠2=∠D=45°,根据等腰三角形的性质得到∠4=∠6=67.5°,由平角的定义得到∠DEC=180°﹣∠6=112.5°.
【小结】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL
12.(2017?恩施州)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.
【分析】利用“边角边”证明△ACD和△BCE全等,可得可得∠CAE=∠CBD,根据“八字型”证明∠AOP=∠PCB=60°即可.
【小结】本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
解题模型四
平移+旋转模型
针对训练
13.(2018?菏泽)如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.
【分析】结论:DF=AE.只要证明△CDF≌△BAE即可;
【解答】解:结论:DF=AE.
理由:∵AB∥CD,
∴∠C=∠B.
∵CE=BF,
∴CF=BE.
又∵CD=AB,
∴△CDF≌△BAE(SAS).
∴DF=AE.
【小结】本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型
14.(2017?孝感)如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD
【分析】根据全等三角形的判定与性质,可得∠B=∠D,根据平行线的判定,可得答案.
【小结】本题考查了全等三角形的判定与性质,利用等式的性质得出BE=DF是解题关键,又利用了全等三角形的判定与性质.
15.(2018?铜仁)已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥FB.
【分析】可证明△ACE≌△BDF,得出∠A=∠B,即可得出AE∥BF;
【小结】本题考查了全等三角形的判定及性质以及平行线的判定问题,关键是SSS证明△ACE≌△BDF.
16.(2018?怀化)已知:如图,点A,F,E,C在同一直线上,AB∥DC,AB=CD,∠B=∠D.
(1)求证:△ABE≌△CDF;
(2)若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.
【分析】(1)根据平行线的性质得出∠A=∠C,进而利用全等三角形的判定证明即可;
(2)利用全等三角形的性质和中点的性质解答即可.
【解答】证明:(1)∵AB∥DC,∴∠A=∠C.
在△ABE与△CDF中,,∴△ABE≌△CDF(ASA).
(2)∵点E,G分别为线段FC,FD的中点,∴ED=CD.
∵EG=5,∴CD=10.
∵△ABE≌△CDF,∴AB=CD=10.
【小结】此题考查全等三角形的判定和性质,关键是根据平行线的性质得出∠A=∠C.
解题模型五
角平分线模型
针对训练
17.(2016?咸宁)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,
.
求证:
.
请你补全已知和求证,并写出证明过程.
【分析】根据图形写出已知条件和求证,利用全等三角形的判定得出△PDO≌△PEO,由全等三角形的性质可得结论.
【小结】本题主要考查了角平分线的性质和全等三角形的性质及判定,利用图形写出已知条件和求证是解答此题的关键.
解题模型六
三垂直模型
针对训练
18.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.
【分析】先证明∠BCE=∠CAD,再证明△ADC≌△CEB,可得到AD=CE,DC=EB,等量代换,可得出DE=AD+BE.
【小结】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.证明两线段的和等于一条线段常常借助三角形全等来证明,要注意运用这种方法
19.如图,将等腰直角三角形ABC的直角顶点置于直线l上,且过A,B两点分别作直线l的垂线,垂足分别为D,E,请你在图中找出一对全等三角形,并写出证明它们全等的过程.
【分析】分析图可知,全等三角形为:△ACD≌△CBE.根据这两个三角形中的数量关系选择ASA证明全等.
【小结】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
专题三
相似三角形解题模型
解题模型一
A字型
针对训练
1.(2015?湘潭)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
【分析】(1)根据折叠的性质得出∠C=∠AED=90°,利用∠DEB=∠C,∠B=∠B证明三角形相似即可;
(2)由折叠的性质知CD=DE,AC=AE.根据题意在Rt△BDE中运用勾股定理求DE,进而得出AD即可.
【解答】证明:(1)∵∠C=90°,△ACD沿AD折叠,
【小结】本题考查了相似三角形的判定和性质,关键是根据1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、勾股定理求解.
2.(2018?黄石)在△ABC中,E、F分别为线段AB、AC上的点(不与A、B、C重合).
(1)如图1,若EF∥BC,求证:
(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若EF上一点G恰为△ABC的重心,,求的值.
【分析】(1)由EF∥BC知△AEF∽△ABC,据此得=,根据=()2即可得证;
(2)分别过点F、C作AB的垂线,垂足分别为N、H,据此知△AFN∽△ACH,得=,
根据=即可得证;
(3)连接AG并延长交BC于点M,连接BG并延长交AC于点N,连接MN,
由重心性质知S△ABM=S△ACM、=,设=a,
利用(2)中结论知==、==a,
从而得==+a,
结合==a可关于a的方程,解之求得a的值即可得出答案.
∴=.
∴==.
(3)如图2,连接AG并延长交BC于点M,连接BG并延长交AC于点N,连接MN,则MN分别是BC、AC的中点,
【小结】本题主要考查相似形的综合问题,解题的关键是熟练掌握相似三角形的判定与性质和三角形重心的定义及其性质等知识点
3.(2017?衢州)如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D,连接OD.作BE⊥CD于点E,交半圆O于点F.已知CE=12,BE=9.
(1)求证:△COD∽△CBE;
(2)求半圆O的半径r的长.
【分析】(1)由切线的性质和垂直的定义得出∠E=90°=∠CDO,再由∠C=∠C,得出△COD∽△CBE.
(2)由勾股定理求出BC==15,由相似三角形的性质得出比例式,即可得出答案.
【小结】本题考查了切线的性质、相似三角形的判定及其性质、勾股定理;熟练掌握相似三角形的判定与性质是解决问题的关键.
4.(2017?杭州)如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;(2)若AD=3,AB=5,求的值.
【分析】(1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,可证明∠AED=∠ACB,进而可证△ADE∽△ABC;
(2)△ADE∽△ABC,,又易证△EAF∽△CAG,所以,从而可知.
【小结】本题考查相似三角形的判定,解题的关键是熟练运用相似三角形的判定,本题属于中等题型
解题模型二
8字型
针对训练
5.(2018?江西)如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
【分析】根据角平分线定义和平行线的性质求出∠D=∠CBD,求出BC=CD=4,证△AEB∽△CED,得出比例式,求出AE=2CE,即可得出答案.
∴=,∴=,∴AE=2CE
∵AC=6=AE+CE,∴AE=4.
【小结】本题考查了相似三角形的性质和判定和等腰三角形的判定、平行线的性质等知识点,能求出AE=2CE和△ABE∽△CDE是解此题的关键.
6.(2017?来宾)如图,在正方形ABCD中,H为CD的中点,延长AH至F,使AH=3FH,过F作FG⊥CD,垂足为G,过F作BC的垂线交BC的延长线于点E.
(1)求证:△ADH∽△FGH;(2)求证:四边形CEFG是正方形.
【分析】(1)由正方形的性质以及FG⊥CD得出∠ADH=∠FGH=90°,结合对顶角∠AHD=∠FHG,即可判定△ADH∽△FGH;
(2)根据三角形相似的性质得出GF=CG,再根据已知条件FG⊥CD,DC⊥BE,FE⊥BE,即可判定四边形CEFG是正方形.
∴==3.
∵GF=AD,DH=CH,∴CG=2GH,∴CD=6GH.
∴CG=CD.
∴GF=CG.
∵FG⊥CD,DC⊥BE,FE⊥BE,
∴四边形CEFG是正方形.
【小结】本题考查了相似三角形的判定和性质,正方形的判定和性质,熟练掌握性质定理是解题的关键.
解题模型三
母子型
针对训练
7.(2018?东营)如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)求证:∠CAD=∠BDC(2)若BD=AD,AC=3,求CD的长.
求出CD的长.
【解答】(1)证明:连接OD,如图所示
∴CD=2.
【小结】本题考查了相似三角形的判定与性质、圆周角定义以及切线的性质,解题的关键是:(1)利用等角的余角相等证出∠CAD=∠BDC;(2)利用相似三角形的性质找出
解题模型四
一线三等角型
针对训练
8.(2018?杭州)如图,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD.(2)若AB=13,BC=10,求线段DE的长.
【分析】(1)想办法证明∠B=∠C,∠DEB=∠ADC=90°即可解决问题;
(2)利用面积法:?AD?BD=?AB?DE求解即可;
【小结】本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,学会利用面积法确定线段的长.
9.(2018?盐城节选)如图,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.
(1)若AB=6,AE=4,BD=2,则CF=
;
(2)求证:△EBD∽△DCF.
【分析】(1)先求出BE的长度后发现BE=BD的,又∠B=60°,可知△BDE是等边三角形,可得∠BDE=60°,另外∠DEF=60°,可证得△CDF是等边三角形,从而CF=CD=BC﹣BD;
(2)证明△EBD∽△DCF,这个模型可称为“一线三等角?相似模型”,根据“AA”判定相似.
∴∠CDF+BDE=120°,∠BED+∠BDE=120°.
∴∠BED=∠CDF.
又∠B=∠C=60°,
∴△EBD∽△DCF.
10.(2017?东营)如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
【解答】证明:(1)∵△ABC是等腰三角形,且∠BAC=120°,
∴∠ABD=∠ACB=30°.
∴∠ABD=∠ADE=30°.
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB.
∴△ABD∽△DCE.
(2)如图1,∵AB=AC=2,∠BAC=120°,
(3)当AD=DE时,如图2,
由(1)可知:此时△ABD≌△DCE,则AB=CD,即2=2﹣x,
x=2﹣2,代入y=x+2,
解得y=4﹣2,即AE=4﹣2.
当AE=ED时,如图3,∠EAD=∠EDA=30°,∠AED=120°,
∴∠DEC=60°,∠EDC=90°,
则ED=EC,即y=(2﹣y).解得y=,即AE=.
当AD=AE时,∠AED=∠EDA=30°,∠EAD=120°,
此时点D与点B重合,不符合题意,此情况不存在,
∴当△ADE是等腰三角形时,AE=4﹣2或.
【小结】本题是相似形的综合题,考查了三角形相似的性质和判定、等腰三角形的性质、直角三角形30°角的性质,本题的几个问题全部围绕△ABD∽△DCE,解决问题;难度适中.
解题模型五
一线三垂直型
针对训练
11.(2018?梧州)如图,AB是⊙M的直径,BC是⊙M的切线,切点为B,C是BC上(除B点外)的任意一点,连接CM交⊙M于点G,过点C作DC⊥BC交BG的延长线于点D,连接AG并延长交BC于点E.
(1)求证:△ABE∽△BCD;
(2)若MB=BE=1,求CD的长度.
【分析】(1)根据直径所对圆周角和切线性质,证明三角形相似;
(2)利用勾股定理和面积法得到AG、GE,根据三角形相似求得GH,得到MB、GH和CD的数量关系,求得CD.
【解答】(1)证明:∵BC为⊙M切线
∴∠ABC=90°.
∵DC⊥BC,
∴∠BCD=90°.
∴∠ABC=∠BCD.
∵AB是⊙M的直径,
∴∠AGB=90°,即BG⊥AE.
∴∠CBD=∠A.
∴△ABE∽△BCD.
(2)解:过点G作GH⊥BC于点H.
∴GH=.
又∵GH∥AB,
【小结】本题是几何综合题,综合考察了圆周角定理、切线性质和三角形相似.解答时,注意根据条件构造相似三角形.
12.(2018?武汉)在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,,直接写出tan∠CEB的值.
【分析】(1)利用同角的余角相等判断出∠BAM=∠CBN,即可得出结论;
(2)先判断出MP=MC,进而得出=,设MN=2m,PN=m,
根据勾股定理得,PM==3m=CM,即可得出结论;
(3)先判断出=,再同(2)的方法,即可得出结论.
【解答】解:(1)∵AM⊥MN,CN⊥MN,
∴∠AMB=∠BNC=90°.
∴∠BAM+∠ABM=90°.
∵∠ABC=90°,
(3)在Rt△ABC中,sin∠BAC==,
如图3,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于点H.
∵∠DEB=90°,∴CH∥AG∥DE,∴=.
同(1)的方法得,△ABG∽△BCH,∴.
设BG=4m,CH=3m,AG=4n,BH=3n,
∵AB=AE,AG⊥BE,∴EG=BG=4m.
【小结】此题是相似形综合题,主要考查了同角的余角相等,相似三角形的判定和性质,锐角三角函数,平行线分线段成比例定理,构造图1是解本题的关键.
专题四
三角函数应用解题模型
解题模型一
“独立”型
图形
关系式
针对训练
1.(2018?台州)图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
【小结】本题考查了解直角三角形的应用:先将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题),然后利用勾股定理和三角函数的定义进行几何计算
解题模型二
“背靠背”型
图形
关系式
针对训练
2.(2018?临沂)如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2(+1)m.请计算说明,工人师傅搬运此钢架能否通过一个直径为2.1m的圆形门?
【小结】本题考查了解直角三角形的应用,解一元一次方程等知识点,能正确求出BD的长是解此题的关键.
3.(2018?长沙)为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)
(2)∵cos30°=,BC=80(千米),∴BD=BC?cos30°=80×(千米).
∵tan45°=,CD=40(千米),∴AD=(千米).
∴AB=AD+BD=40+40≈40+40×1.73=109.2(千米).
∴汽车从A地到B地比原来少走多少路程为:AC+BC﹣AB=136.4﹣109.2=27.2(千米).
【小结】本题考查了勾股定理的运用以及解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
4.(2018?陇南)随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:≈1.7,≈1.4)
答:隧道打通后与打通前相比,从A地到B地的路程将约缩短224公里.
【小结】本题考查的是解直角三角形的应用﹣方向角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,需要熟记锐角三角函数的定义.
5.(2018?常州)京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
【小结】此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.
6.(2017?岳阳)某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.
(1)求支架CD的长;
(2)求真空热水管AB的长.(结果保留根号)
【小结】此题主要考查了解直角三角形的应用,要熟练掌握,注意将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
7.(2017?赤峰)王浩同学用木板制作一个带有卡槽的三角形手机架,如图所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
【解析】根据题意作出合适的辅助线,可以求得AD和CD的长,进而可以求得DB的长,然后根据勾股定理即可得到AB的长,然后与17比较大小,即可解答本题.
【小结】本题考查解直角三角形的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用直角三角形的相关知识解答
解题模型三
“母抱子”型
图形
关系式
针对训练
8.(2017?白银)美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
【小结】本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型
9.(2017?宜宾)如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A,又在河的另一岸边取两点B、C测得∠α=30°,∠β=45°,量得BC长为100米.求河的宽度(结果保留根号).
【小结】此题主要考查了解直角三角形的应用,正确得出AD=CD是解题关键.
10.(2016?青海)如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)求办公楼AB的高度;(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈,cos22°,tan22)
【小结】此题主要考查了解直角三角形的应用,根据已知得出tan22°=是解题关键.
11.(2016?六盘水)据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
【解析】(1)在直角三角形ABD与直角三角形ACD中,利用锐角三角函数定义求出BD与CD的长,由BD﹣CD求出BC的长即可;
(2)根据路程除以时间求出该轿车的速度,即可作出判断.
解:(1)在Rt△ABD中,AD=24m,∠B=31°,
∴tan31°=,即BD==40m.
在Rt△ACD中,AD=24m,∠ACD=50°,
∴tan50°=,即CD==20m.
∴BC=BD﹣CD=40﹣20=20m.
则BC的距离为20m.
(2)根据题意,得20÷2=10m/s<15m/s,
则此轿车没有超速.
【小结】此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.
12.(2016?兰州)如图,一垂直于地面的灯柱AB被一钢线CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
【小结】本题考查解直角三角形的应用,解题的关键是明确题意,利用三角函数值求出相应的边的长度.
13.(2017?张家界)位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
【小结】此题主要考查了解直角三角形的应用,正确掌握锐角三角函数关系是解题关键
14.(2017?呼和浩特)如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(结果用含非特殊角的三角函数和根式表示即可)
【解析】过点C作CM⊥AB交AB延长线于点M,通过解直角△ACM得到AM的长度,通过解直角△BCM得到BM的长度,则AB=AM﹣BM.
【小结】本题考查解直角三角形的应用、三角函数等知识,解题的关键是添加辅助线,构造直角三角形,记住三角函数的定义,以及特殊三角形的边角关系,属于中考常考题型.
15.(2018?烟台)汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
【解析】先求得AC=PCtan∠APC=87、BC=PCtan∠BPC=21,据此得出AB=AC﹣BC=87﹣21=66,从而求得该车通过AB段的车速,比较大小即可得.
解:在Rt△APC中,AC=PCtan∠APC=30tan71°≈30×2.90=87,
在Rt△BPC中,BC=PCtan∠BPC=30tan35°≈30×0.70=21,
则AB=AC﹣BC=87﹣21=66,
∴该汽车的实际速度为=11m/s.
又∵40km/h≈11.1m/s,
∴该车没有超速.
【小结】此题考查了解直角三角形的应用,涉及的知识有:锐角三角函数定义,熟练掌握三角函数的定义是解本题的关键.
16.(2017?铁岭)如图,某市文化节期间,在景观湖中央搭建了一个舞台C,在岸边搭建了三个看台A,B,D,其中A,C,D三点在同一条直线上,看台A,B到舞台C的距离相等,测得∠A=30°,∠D=45°,AB=60m,小明、小丽分别在B,D看台观看演出,请分别求出小明、小丽与舞台C的距离.(结果保留根号)
【解析】如图作BH⊥AD于H.,CE⊥AB于E.解直角三角形,分别求出BC、CD即可解决问题.
解:如图,作BH⊥AD于点H,CE⊥AB于点E.
∴BH=DH=30.
∴DC=DH+CH=30+10.
答:小明、小丽与舞台C的距离分别为20m和(30+10)m.
【小结】本题考查解直角三角形、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
17.(2017?广元)如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).
【小结】本题考查解直角三角形的应用,解答本题的关键是明确题意,利用特殊角的三角函数值解答.
18.(2017?贵阳)贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
【小结】本题考查了解直角三角形的应用,首先构造直角三角形,再运用三角函数的定义解题,构造出直角三角形是解题的关键.
19.(2017?西宁)如图,建设“幸福西宁”,打造“绿色发展样板城市”.美丽的湟水河宛如一条玉带穿城而过,已形成“水清、流畅、岸绿、景美”的生态环境新格局.在数学课外实践活动中,小亮在海湖新区自行车绿道北段AC上的A,B两点分别对南岸的体育中心D进行测量,分别测得∠DAC=30°,∠DBC=60°,AB=200米,求体育中心D到湟水河北岸AC的距离约为多少米(精确到1米,≈1.732)?
【小结】本题考查了解直角三角形的应用.主要是正切概念及运算,关键把实际问题转化为数学问题加以计算
解题模型四
“斜截”型
图示:辅助线作法——延长四边形对边法
针对训练
20.(2016?娄底)芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)
解得x=10﹣,∴BH=2+(10﹣)=10﹣1≈16.3(米).答:立柱BH的长约为16.3米.
【小结】本题考查了解直角三角形的应用;由三角函数求出CH和AH是解决问题的关键.
21.(2018?随州)随州市新?水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;(2)求最长的斜拉索AC的长.
∴AB=3BD=5×3=15.
在Rt△ABH中,∵∠B=45°,
∴BH=AH=AB=×15=15.
在Rt△ACH中,∵∠C=30°,
∴AC=2AH=30.
答:最长的斜拉索AC的长为30m.
【小结】本题考查了解直角三角形的应用:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
22.(2017?凉山州)如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
【解析】延长OC,AB交于点P,△PCB∽△PAO,根据相似三角形对应边比例相等的性质即可解题.
解:如图,延长OC,AB交于点P.
∵∠ABC=120°,
∴∠PBC=60°.
【小结】本题考查了通过作辅助线构建直角三角形的能力,考查了相似三角形的判定和性质,本题中求证△PCB∽△PAO是解题的关键.
解题模型五
其他类型
23.(2018?徐州)如图,1号楼在2号楼的南侧,两楼高度均为90m,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=42m.
(1)求楼间距AB;
(2)若2号楼共30层,层高均为3m,则点C位于第几层?(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
【解析】(1)构造出两个直角三角形,利用两个角的正切值即可求出答案.
24.(2018?资阳)如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米.
(1)当风筝的水平距离AC=18米时,求此时风筝线AD的长度;
(2)当她从点A跑动9米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
答:此时风筝线AD的长度为12米.
方法二:设CD=x,
∵∠CAD=30°,
∴BE=AD=2CD=2x,AC===x.
∵CF=10,
∴AF=AC﹣CF=x﹣10.
∵AB=9,
∴BF=AB+AF=9+x﹣10.
∵∠EBF=45°,
∴由cos∠EBF=可得=.
解得x=12+,即CD=12+,
则C1D=CD+C1C=12++=+.
答:风筝原来的高度C1D为(+)米.
【小结】本题主要考查解直角三角形的应用,解题的关键是掌握三角函数的定义及根据题意找到两直角三角形间的关联.
25.(2018?常德)图1是一商场的推拉门,已知门的宽度AD=2米,且两扇门的大小相同(即AB=CD),将左边的门ABB1A1绕门轴AA1向里面旋转37°,将右边的门CDD1C1绕门轴DD1向外面旋转45°,其示意图如图2,求此时B与C之间的距离(结果保留一位小数).(参考数据:sin37°≈0.6,cos37°≈0.8,≈1.4)
∴BE∥CM.
又∵BE=CM,
∴四边形BEMC为平行四边形.
∴BC=EM,CM=BE.
在Rt△MEF中,EF=AD﹣AE﹣DF=0.5,FM=CF+CM=1.3,
∴EM=≈1.4.
∴B与C之间的距离约为1.4米.
【小结】本题考查了解直角三角形的应用、勾股定理以及平行四边形的判定与性质,构造直角三角形,利用勾股定理求出BC的长度是解题的关键.
26.(2018?岳阳)图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:≈1.73,结果精确到0.01米)
∴ON=OM=0.6,∴NB=ON+OB=3.3+0.6=3.9,即点M到地面的距离是3.9米
【小结】本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会添加常用辅助线,在直角三角形解决问题,属于中考常考题型.
27.(2017?桂林)“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
【解析】在Rt△BED中可先求得BE的长,过点C作CF⊥AE于点F,则可求得AF的长,从而可求得EF的长,即可求得CD的长.
解:∵BN∥ED,
【小结】本题主要考查解直角三角形的应用,利用条件构造直角三角形是解题的关键,注意角度的应用.
28.(2017?常德)如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,≈1.732,≈1.414)
【小结】本题考查解直角三角形、锐角三角函数、解题的关键是添加辅助线,构造直角三角形,记住锐角三角函数的定义,属于中考常考题型。
专题五
反比例函数K的几何意义解题模型
解题模型一
图形
关系式
S阴影=|k|
针对训练
1.(2018?毕节)已知点P(﹣3,2),点Q(2,a)都在反比例函数y=(k≠0)的图象上,过点Q分别作两坐标轴的垂线,两垂线与两坐标轴围成的矩形面积为( )
A.3
B.6
C.9
D.12
【小结】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
2.(2017?阜新)在平面直角坐标系中,点P是反比例函数y=(x<0)图象上的一点,分别过点P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为6,则k的值是
【小结】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
3.(2018?相山区三模)如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为4,则这个反比例函数的解析式为
.
【解析】过A点向x轴作垂线,与坐标轴围成的四边形的面积是定值|k|,由此可得出答案.
解:过A点向x轴作垂线,如图:
根据反比例函数的几何意义可得:四边形ABCD的面积为4,即|k|=4,
又∵函数图象在二、四象限,∴k=﹣4,即函数解析式为:y=﹣.
【点评】本题考查了反比例函数的几何意义,解答本题关键是掌握在反比例函数中k所代表的几何意义,属于基础题,难度一般.
解题模型二
图形
关系式
S阴影=
针对训练
4.(2017?铜仁)如图,已知点A在反比例函数y=上,AC⊥x轴,垂足为点C,且△AOC的面积为4,则此反比例函数的表达式为( )
A.y=
B.y=
C.y=
D.y=﹣
【解析】由S△AOC=xy=4,设反比例函数的解析式y=,则k=xy=8
解:∵S△AOC=4,
∴k=2S△AOC=8;
∴y=;
故选:C.
【小结】此题考查了待定系数法求反比例函数解析式,反比例函数系数k的几何意义.属于基础题,难度不大
5.(2018?苏州)如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=,则k的值为( )
A.3
B.2
C.6
D.12
∴k=12a2=(4+4a)a,
解得:a=或a=0(舍),
则k=12×=3,
故选:A.
【小结】本题主要考查反比例函数图象上点的坐标特征,解题的关键是根据题意表示出点D、E的坐标及反比例函数图象上点的横纵坐标乘积都等于反比例系数k.
6.(2018?娄底)如图,在平面直角坐标系中,O为坐标原点,点P是反比例函数y=图象上的一点,PA⊥x轴于点A,则△POA的面积为
.
【小结】此题主要考查了反比例函数系数k的几何意义,正确表示出△POA的面积是解题关键.
7.(2017?永州)如图,已知反比例函数y=(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=
.
【解析】根据反比例函数的性质可以得到△AOB的面积等于|k|的一半,由此可以得到它们的关系.
解:依据比例系数k的几何意义可得两个三角形的面积都等于|k|=1,解得k=﹣2,
故答案为:﹣2.
【小结】本题考查反比例系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.
8.(2018?衢州)如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连接OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=
.
【小结】此题考查了反比例函数系数k的几何意义,以及反比例函数图象上点的坐标特征,熟练掌握反比例函数k的几何意义是解本题的关键
解题模型三
图形
关系式
S△ABC=|k|
S△APP1=2|k|
针对训练
9.(2018?江干区一模)下列与反比例函数图象有关图形中,阴影部分面积最小的是( )
A.
B.
C.
D.
【点评】本题考查反比例函数系数k的几何意义,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
10.(2018?凤城市模拟)如图,A,B是函数y=图象上关于原点对称的两点,BC∥x轴,AC∥y轴,若△ABC的面积为8,则k的值是
.
【点评】本题考查的是反比例函数的性质,熟知反比例函数系数k的几何意义是解答此题的关键.
解题模型四
图形
关系式
针对训练
11.(2018?郴州)如图,A,B是反比例函数y=在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是(
【点评】本题考查了反比例函数中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|.也考查了反比例函数图象上点的坐标特征,梯形的面积.
12.(2018?铜梁区模拟)如图,已知A、B两点是反比例函数y=(x>0)的图象上任意两点,过A、B两点分别作y轴的垂线,垂足分别为C、D,连接AB、AO、BO,则四边形ABDC的面积与△AOB的面积之比值( )
A.等于1
B.小于1
C.大于1
D.不确定
【点评】本题考查了反比例函数y=(k≠0)系数k的几何意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|
解题模型五
图形
关系式
S阴影=
S阴影=
针对训练
13.(2018?徐州)如图,在平面直角坐标系中,函数y=kx与y=﹣的图象交于A,B两点,过A作y轴的垂线,交函数y=的图象于点C,连接BC,则△ABC的面积为( )
A.2
B.4
C.6
D.8
∴S△ABC=×(﹣2x﹣x)?(﹣﹣)=×(﹣3x)?(﹣)=6.
故选:C.
【小结】本题考查了反比例函数与正比例函数图象的特点,垂直于y轴的直线上任意两点的坐标特点,三角形的面积,解答此题的关键是找出A、B两点与A、C两点坐标的关系.
14.(2018?贵阳)如图,过x轴上任意一点P作y轴的平行线,分别与反比例函数y=(x>0),y=﹣(x>0)的图象交于A点和B点,若C为y轴任意一点.连接AC、BC,则△ABC的面积为
.
【小结】本题考查反比例函数中比例系数k的几何意义,本题也可直接套用结论求解.
15.(2018?黑龙江)如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=(x>0)、y=(x<0)的图象于B、C两点,若△ABC的面积为2,则k值为( )
A.﹣1
B.1
C.
D.
【小结】本题考查了反比例函数系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.
解题模型六
图示:
针对训练
16.(2018?宁波)如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为( )
A.8
B.﹣8
C.4
D.﹣4
【小结】本题考查了反比例函数图象上点的坐标特征,点在函数的图象上,则点的坐标满足函数的解析式.也考查了三角形的面积.
17.(2018?唐河县三模)如图,设点P在函数y=的图象上,PC⊥x轴于点C,交函数y=的图象于点A,PD⊥y轴于点D,交函数y=的图象于点B,则四边形PAOB的面积为 4 .
【小结】本题考查了比例系数k的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|
专题六线段最值问题解题模型
解决几何最值问题的理论依据有:①两点之间线段最短;②垂线段最短;③三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值);④定圆中的所有弦中,直径最长;⑤圆外一点与圆心的连线上,该点和此直线与圆的近交点距离最短、远交点距离最长.根据不同特征转化从而减少变量是解决最值问题的关键,直接套用基本模型是解决几何最值问题的高效手段.
解题模型一
图形
转化
直线l外有一定点A,点B是直线l上的一个动点,求AB的最小值.
过定点A作AB⊥l于点B.
针对训练
1.(2018?长春)如图,在?ABCD中,AD=7,AB=2,∠B=60°.E是边BC上任意一点,沿AE剪开,将△ABE沿BC方向平移到△DCF的位置,得到四边形AEFD,则四边形AEFD周长的最小值为 20 .
【小结】此题考查平移的性质,关键是根据当AE⊥BC时,四边形AEFD的周长最小进行分析
解题模型二
图形
转化
A,B为定点,l为定直线,P为直线l上的一个动点,求AP+BP的最小值.
作其中一个定点关于定直线l的对称点,连接对称点与另一定点.
点A是l上的动点,B,P是定点,求PA+AB最小值.
作点P关于直线l1的对称点P’,则P’B为PA+AB的最小值.
针对训练
2.(2018?天津)如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的
【小结】本题考查的是轴对称,最短路线问题,根据题意作出A关于BD的对称点C是解答此题的关键.
3.(2018?十堰)如图,Rt△ABC中,∠BAC=90°,AB=3,AC=6,点D,E分别是边BC,AC上的动点,则DA+DE的最小值为
.
∵∠A'FD=∠DEC=90°,∠A'DF=∠CDE,
∴∠A'=∠C,
∵∠AEA'=∠BAC=90°,
∴△AEA'∽△BAC,
∴,
∴,
∴A'E=,
即AD+DE的最小值是;
【小结】本题考查轴对称﹣最短问题、三角形相似的性质和判定、两点之间线段最短、垂线段最短等知识,解题的关键是灵活运用轴对称以及垂线段最短解决最短问题,属于中考填空题中的压轴题.
解题模型三
图形
转化
P为定点,M,N为定直线上的动点,求△PMN周长的最小值.
过定点P分别作关于两条定直线的对称点,连接两对称点.
求直线l1,l2上的点M,N,使得四边形PQMN的周长最小.
作定点Q关于直线l1的对称点Q’,作定点P关于直线l2的对称点P’,连接Q’P’,分别交直线l1,l2于点M,N
针对训练
4.(2015?营口)如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数
∵△PMN周长的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°;
【小结】本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质;熟练掌握轴对称的性质,证明三角形是等边三角形是解决问题的关键.
5.(2015?玉林)如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
∵AD=A′D=3,BE=BE′=1,∴AA′=6,AE′=4.
∵DQ∥AE′,D是AA′的中点,∴DQ是△AA′E′的中位线,
【小结】本题考查了轴对称,利用轴对称确定A′、E′,连接A′E′得出P、Q的位置是解题关键,又利用了相似三角形的判定与性质,图形分割法是求面积的重要方法.
解题模型四
图形
转化
直线m∥n,在m,n上分别求点M,N,使MN⊥m,且AM+MN+BN的值最小
将点A向下平移MN的单位长度得A′,连接A′B,交n于点N,过点N作MN⊥m于M,点M,N即为所求.
在直线l上求两点M,N(M在左),使MN=a,并使AM+MN+NB的值最小.
将点A向右平移a个长度单位得A′,作A′关于l的对称点A″,连接A″B,交直线l于点N,将N点向左平移a个单位长度得M.
针对训练
6.(2017?内江)如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=
.
【小结】本题考查轴对称﹣最短问题、平行线的性质、平行四边形的判定和性质、勾股定理等知识,解题的关键是学会构建平行四边形解决问题,属于中考常考题型
解题模型五
图形
转化
P是圆上一动点,求AP的最大值和最小值.
当P点运动到点B时,AP取得最小值;当P点运动到点C时,AP取得最大值.
P为圆内一定点,求过点P的弦的最小值与最大值.
AB是过圆O内定点P的弦.当OP⊥AB时,过点P的弦的最小值为线段AB;过点P的弦的最大值为圆的直径.
针对训练
7.(2015?自贡)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A.2﹣2
B.6
C.2﹣2
D.4
∴AE=EB′=2,
∵AD=6,
∴DE==2,
∴DB′=2﹣2.
故选:A.
【小结】本题主要考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用,确定点B′在何位置时,B′D的值最小,是解决问题的关键.
8.(2018?内江)如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O的半径r=2,直线AB不垂直于直线l,过点A,B分别作直线l的垂线,垂足分别为点D,C,则四边形ABCD的面积的最大值为 12 .
【小结】本题考查了梯形中位线:梯形的中位线平行于两底,并且等于两底和的一半.
解题模型六
图例[]
圆柱
则AB2=B′A2+B′B2
长
方
体
阶梯
问题
基本
思路
将立体图形展开成平面图形→利用两点之间线段最短确定最短路线→构造直角三角形→利用勾股定理求解
针对训练
9.(2018?黄冈)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 20 cm(杯壁厚度不计).
【解析】将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解:如图:将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B===20(cm).故答案为20.
【小结】本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
10.(2017?东营)我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 25 尺.
【小结】本题考查了平面展开最短路径问题,关键是把立体图形展成平面图形,本题是展成平面图形后为直角三角形按照勾股定理可求出解.
专题七
等腰三角形综合题解题模型
解题模型一
等边三角形共顶点
等边△ABC与等边△DCE,B、C、E三点共线.
连接BD、AE交于点F,BD交AC于点G,AE交DC于点H,连接CF、GH,则:
(1)△BCD≌△ACE;
(2)AE=BD;
(3)∠AFB=∠DFE=60°;
(4)FC平分∠BFE;
(5)BF=AF+FC,EF=DF+FC;
(6)△CGH为等边三角形.
针对训练
1.(2017?恩施)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.
【答案】证明:∵△ABC和△ECD都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°.
∴∠ACB+∠BCE=∠DCE+∠BCE,即∠ACE=∠BCD.
在△ACE和△BCD中,,
∴△ACE≌△BCD(SAS).
∴∠CAE=∠CBD.
∵∠APC=∠BPO,
∴∠BOP=∠ACP=60°,即∠AOB=60°.
【小结】本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
解题模型二
等腰直角三角形共顶点
等腰Rt△ABC与等腰Rt△DCE中,∠ACB=∠DCE=90°.
如图1,连接BD、AE交于点F,连接FC、AD、BE,则:
(1)△BCD≌△ACE;
(2)AE=BD;
(3)AE⊥BD;
(4)FC平分∠BFE;
(5)AB2+DE2=AD2+BE2
(6)BF=AF+FC,EF=DF+FC;
(7)如图2,若G、I分别为BE、AD的中点,则GC⊥AD、IC⊥BE(反之亦然);
(8)S△ACD=S△BCE.
针对训练
2.(2018?东营)如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )
A.①②③④
B.②④
C.①②③
D.①③④
【小结】本题考查全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考选择题中的压轴题.
3.(2017?哈尔滨)已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.
(1)如图1,求证:AE=BD;[]
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
【解析】(1)∵△ACB和△DCE都是等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,DC=EC.
∴∠ACB+∠ACD=∠DCE+∠ACD.
∴∠BCD=∠ACE.
在△ACE与△BCD中,
∴△ACE≌△BCD(SAS).
∴AE=BD.
(2)由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC,
∴∠DOM=90°.
∵∠AEC=∠CAE=∠CBD,
∴△EMC≌△BCN(ASA).
∴CM=CN,
∴DM=AN.
∴△AON≌△DOM(AAS).
∵DE=AB,AO=DO,
∴△AOB≌△DOE(HL).
【小结】本题考查全等三角形,解题的关键是熟练运用全等三角形的判定条件,本题属于基础题型.
解题模型三
等腰三角形共顶点
等腰△ACB与等腰△DCE中,AC=BC,DC=CE,且∠ACB=∠DCE.
连接BD,AE交于点F,则:
(1)△BCD≌△ACE;
(2)AE=BD;
(3)∠AFB=∠ACB;
(4)FC平分∠BFE.
针对训练
4.(2018?河南)(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①的值为 1 ;②∠AMB的度数为 40° .
(2)类比探究:如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由;
(3)拓展延伸:在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=,请直接写出当点C与点M重合时AC的长.
(3)正确画图形,当点C与点M重合时,有两种情况:如图3和4,同理可得:△AOC∽△BOD,则∠AMB=90°,,可得AC的长.
故答案为:①1;②40°.
(2)类比探究
如图2,=,∠AMB=90°,理由是:Rt△COD中,∠DCO=30°,∠DOC=90°,∴.
同理得:,∴.
∵∠AOB=∠COD=90°,∴∠AOC=∠BOD,∴△AOC∽△BOD.[]∴=,∠CAO=∠DBO.
在△AMB中,∠AMB=180°﹣(∠MAB+∠ABM)=180°﹣(∠OAB+∠ABM+∠DBO)=90°.
(3)拓展延伸
【小结】本题是三角形的综合题,主要考查了三角形全等和相似的性质和判定,几何变换问题,解题的关键是能得出:△AOC∽△BOD,根据相似三角形的性质,并运用类比的思想解决问题,本题是一道比较好的题目.
同课章节目录
