湖南省蓝山二中2011-2012学年高二上学期期末考试数学(文)试题
文档属性
| 名称 | 湖南省蓝山二中2011-2012学年高二上学期期末考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 222.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-13 00:00:00 | ||
图片预览



文档简介
时量:120分钟 满分:100分
一、选择题(本大题共15小题,每小题3分,共45分)
1.“”是“” 的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
2.双曲线的渐近线方程是( )
A. B. C. D.
3.顶点在原点,且过点的抛物线的标准方程是( )
A. B.
C.或 D.或
4. 已知是正三角形,某椭圆以A、B为焦点,且经过点C,则其离心率等于( )
A. B. C. D.
5.以椭圆的顶点为焦点,焦点为顶点的双曲线方程是( )
A. B. C. D.
6. 在复平面内,复数 对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7.某工程的工序流程图如下(工时数单位,天),则工程总时数为 ( )
8.用反证法证明命题:若整系数一元二次方程有有理数根,
那么、、中至少有一个是偶数时,下列假设中正确的是( )
A.假设、、都是偶数 B.假设、、都不是偶数
C.假设、、至多有一个偶数 D.假设、、至多有两个偶数
9.函数的单调递减区间为( )
A.(,1) B.(1,)
C.(0,1) D.(1,e)
10.曲线在处的切线的斜率等于( )
A. 3 B.-3
C.-2 D. 2
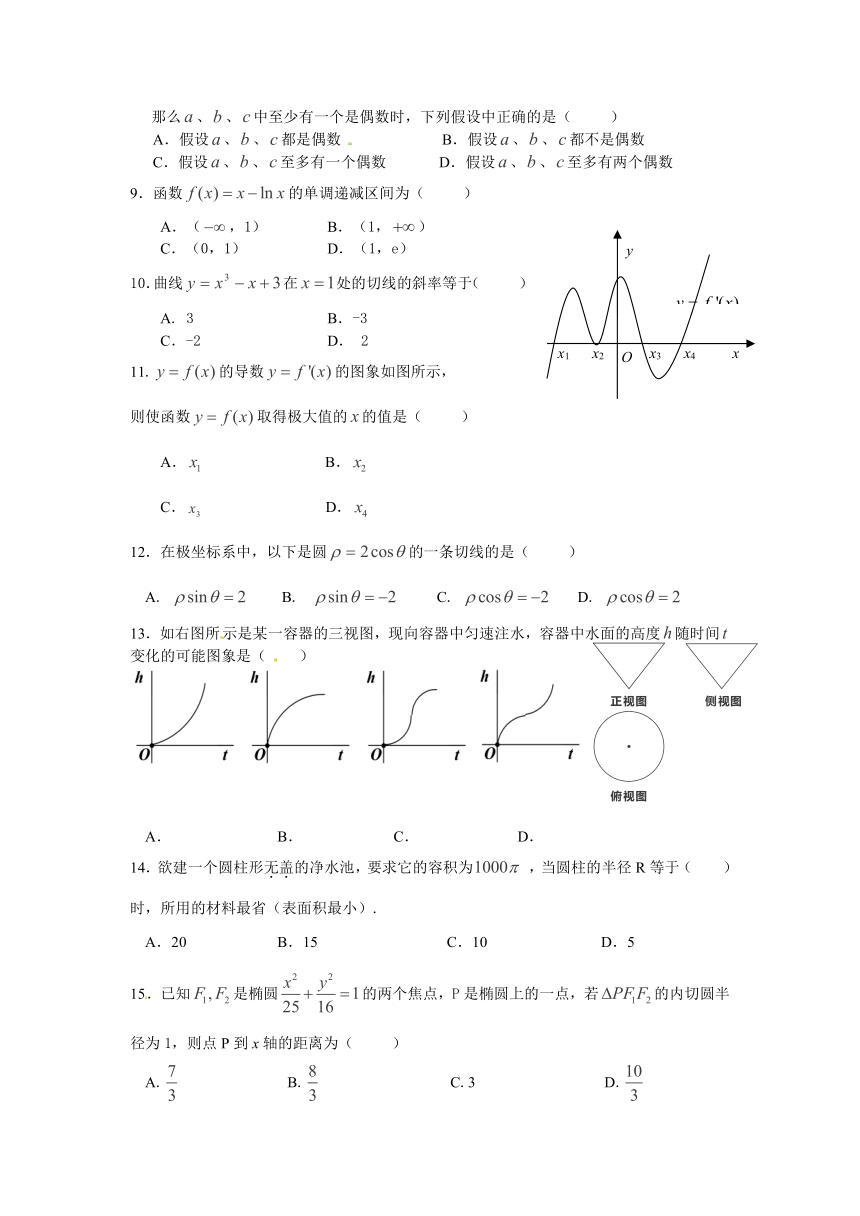
11.的导数的图象如图所示,
则使函数取得极大值的的值是( )
A. B.
C. D.
12.在极坐标系中,以下是圆的一条切线的是( )
A. B. C. D.
13.如右图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )
A. B. C. D.
14.欲建一个圆柱形无盖的净水池,要求它的容积为,当圆柱的半径R等于( )时,所用的材料最省(表面积最小).
A.20 B.15 C.10 D.5
15.已知是椭圆的两个焦点,P是椭圆上的一点,若的内切圆半径为1,则点P到x轴的距离为( )
A. B. C.3 D.
二、填空题(本大题共5小题,每小题3分,共15分)
16.已知曲线C的参数方程为(为参数),
则曲线C的普通方程是
17.如图,在腰长为2的等腰直角三角形ABC内任取一点P,
则点P到直角顶点A的距离小于的概率为
18.某课外小组在调查男女乘客是否晕机的情况中,获得男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,根据列联表的数据,可以有__________的把握认为晕机与性别有关.
数据列联表: 独立性检验临界值表:
P(k2≥k0) 0.10 0.05 0.025 0.010 0.005
k0 2.706 3.841 5.024 6.635 7.879
晕机 不晕机 合计
男乘客 28 28 56
女乘客 28 56 84
合计 56 84 140
独立性检验随机变量K2值的计算公式:
19.已知命题:,若命题是真命题,则实数的取值
范围是
20.已知数列满足,,,类比课本中推导等比数列前项和公式的方法,可求得____ _____
三、解答题(本大题共5小题,共40分,解答应写出文字说明,证明过程或演算步骤)
21.(本题满分6分)
将A、B两枚均匀的骰子各抛掷一次,向上的点数分别为,,
(I)共有多少种结果? (II)“”的概率是多少?
22.(本题满分6分)
请认真阅读下列材料:
“杨辉三角” (1261年)是中国古代重要的数学成就,它比西方的“帕斯卡三角”(1653年)早了300多年(如表1).在“杨辉三角”的基础上德国数学家莱布尼兹发现了下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
请回答下列问题:
(I)记为表1中第n行各个数字之和,求,并归纳出;
(II)根据表2前5行的规律依次写出第6行的数.
23.(本题满分8分)
已知实数,设P:函数在R上单调递减,
Q:关于的一元二次方程有两个不相等的实数根,
如果命题“”为真命题,命题“”为假命题,求实数c的取值范围.
24.(本题满分10分)
椭圆C1:的左、右焦点分别为F1、F2,F2也是抛物线
C2:的焦点,点M为C1与C2在第一象限的交点,且
(I)求C1的方程;
(II)直线l∥OM(为坐标原点),且与C1交于A、B两点,若·=0,
求直线l的方程.
25.(本题满分10分)
已知函数是函数的极值点,
其中是自然对数的底数。
(I)求实数a的值;
(II)直线同时满足:
① 是函数的图象在点处的切线 ,
② 与函数的图象相切于点,
求实数b的取值范围.
高二文科数学参考答案
一、选择题(本大题共15小题,每小题3分,共45分)
二、填空题(本大题共5小题,每小题3分,共15分)
16. 17. 18. 95% 19. 20.
三、解答题(本大题共5小题,共40分,解答应写出文字说明,证明过程或演算步骤)
21.(本题满分6分)
解:(I) 共有种结果 ………………2分
(II) 若用(,)来表示两枚骰子向上的点数,
则“” 的结果有:(2,1),(4,2),(6,3) 共3种 ………………4分
故“”的概率是:P= …………6分
23.(本题满分8分)
解:函数在R上单调递减 ………………2分
关于的一元二次方程有两个不相等的实数根,
………………4分
依题意,P和Q有且仅有一个正确。 ………………5分
如果正确,且不正确,则, ………………6分
如果不正确,且正确,则 ………………7分
实数的取值范围是. ………………8分
24.(本题满分10分)
解:(Ⅰ)由:知.设,在上,
因为,所以,得,. ………………2分
在上,且椭圆的半焦距,于是
消去并整理得,解得(不合题意,舍去).
故椭圆的方程为.………………5分
(或利用定义法求出)
(Ⅱ)因为,所以与的斜率相同,故的斜率.……6分
设的方程为.
由消去并化简得.
设,,,.…………7分
因为,所以.
.所以.
此时,
故所求直线的方程为,或.……………10分
(未验证扣1分)
25.(本题满分10分)
解:(I)
…………2分
由已知,
得a =1 …………4分
(II)时,
函数的图象在点处的切线的方程为:
直线与函数的图象相切于点,
又,所以切线的斜率为
故切线的方程为
即的方程为:
得 …………7分
A.11
B.10
C.8
D.7
y
x1 x2 x3 x4 x
O
A
B
C
P
2
2
晕机 不晕机 合计
男乘客 28 28 56
女乘客 28 56 84
合计 56 84 140
表2
表1
一、选择题(本大题共15小题,每小题3分,共45分)
1.“”是“” 的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
2.双曲线的渐近线方程是( )
A. B. C. D.
3.顶点在原点,且过点的抛物线的标准方程是( )
A. B.
C.或 D.或
4. 已知是正三角形,某椭圆以A、B为焦点,且经过点C,则其离心率等于( )
A. B. C. D.
5.以椭圆的顶点为焦点,焦点为顶点的双曲线方程是( )
A. B. C. D.
6. 在复平面内,复数 对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7.某工程的工序流程图如下(工时数单位,天),则工程总时数为 ( )
8.用反证法证明命题:若整系数一元二次方程有有理数根,
那么、、中至少有一个是偶数时,下列假设中正确的是( )
A.假设、、都是偶数 B.假设、、都不是偶数
C.假设、、至多有一个偶数 D.假设、、至多有两个偶数
9.函数的单调递减区间为( )
A.(,1) B.(1,)
C.(0,1) D.(1,e)
10.曲线在处的切线的斜率等于( )
A. 3 B.-3
C.-2 D. 2
11.的导数的图象如图所示,
则使函数取得极大值的的值是( )
A. B.
C. D.
12.在极坐标系中,以下是圆的一条切线的是( )
A. B. C. D.
13.如右图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )
A. B. C. D.
14.欲建一个圆柱形无盖的净水池,要求它的容积为,当圆柱的半径R等于( )时,所用的材料最省(表面积最小).
A.20 B.15 C.10 D.5
15.已知是椭圆的两个焦点,P是椭圆上的一点,若的内切圆半径为1,则点P到x轴的距离为( )
A. B. C.3 D.
二、填空题(本大题共5小题,每小题3分,共15分)
16.已知曲线C的参数方程为(为参数),
则曲线C的普通方程是
17.如图,在腰长为2的等腰直角三角形ABC内任取一点P,
则点P到直角顶点A的距离小于的概率为
18.某课外小组在调查男女乘客是否晕机的情况中,获得男乘客晕机为28人,不会晕机的也是28人,而女乘客晕机为28人,不会晕机的为56人,根据列联表的数据,可以有__________的把握认为晕机与性别有关.
数据列联表: 独立性检验临界值表:
P(k2≥k0) 0.10 0.05 0.025 0.010 0.005
k0 2.706 3.841 5.024 6.635 7.879
晕机 不晕机 合计
男乘客 28 28 56
女乘客 28 56 84
合计 56 84 140
独立性检验随机变量K2值的计算公式:
19.已知命题:,若命题是真命题,则实数的取值
范围是
20.已知数列满足,,,类比课本中推导等比数列前项和公式的方法,可求得____ _____
三、解答题(本大题共5小题,共40分,解答应写出文字说明,证明过程或演算步骤)
21.(本题满分6分)
将A、B两枚均匀的骰子各抛掷一次,向上的点数分别为,,
(I)共有多少种结果? (II)“”的概率是多少?
22.(本题满分6分)
请认真阅读下列材料:
“杨辉三角” (1261年)是中国古代重要的数学成就,它比西方的“帕斯卡三角”(1653年)早了300多年(如表1).在“杨辉三角”的基础上德国数学家莱布尼兹发现了下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
请回答下列问题:
(I)记为表1中第n行各个数字之和,求,并归纳出;
(II)根据表2前5行的规律依次写出第6行的数.
23.(本题满分8分)
已知实数,设P:函数在R上单调递减,
Q:关于的一元二次方程有两个不相等的实数根,
如果命题“”为真命题,命题“”为假命题,求实数c的取值范围.
24.(本题满分10分)
椭圆C1:的左、右焦点分别为F1、F2,F2也是抛物线
C2:的焦点,点M为C1与C2在第一象限的交点,且
(I)求C1的方程;
(II)直线l∥OM(为坐标原点),且与C1交于A、B两点,若·=0,
求直线l的方程.
25.(本题满分10分)
已知函数是函数的极值点,
其中是自然对数的底数。
(I)求实数a的值;
(II)直线同时满足:
① 是函数的图象在点处的切线 ,
② 与函数的图象相切于点,
求实数b的取值范围.
高二文科数学参考答案
一、选择题(本大题共15小题,每小题3分,共45分)
二、填空题(本大题共5小题,每小题3分,共15分)
16. 17. 18. 95% 19. 20.
三、解答题(本大题共5小题,共40分,解答应写出文字说明,证明过程或演算步骤)
21.(本题满分6分)
解:(I) 共有种结果 ………………2分
(II) 若用(,)来表示两枚骰子向上的点数,
则“” 的结果有:(2,1),(4,2),(6,3) 共3种 ………………4分
故“”的概率是:P= …………6分
23.(本题满分8分)
解:函数在R上单调递减 ………………2分
关于的一元二次方程有两个不相等的实数根,
………………4分
依题意,P和Q有且仅有一个正确。 ………………5分
如果正确,且不正确,则, ………………6分
如果不正确,且正确,则 ………………7分
实数的取值范围是. ………………8分
24.(本题满分10分)
解:(Ⅰ)由:知.设,在上,
因为,所以,得,. ………………2分
在上,且椭圆的半焦距,于是
消去并整理得,解得(不合题意,舍去).
故椭圆的方程为.………………5分
(或利用定义法求出)
(Ⅱ)因为,所以与的斜率相同,故的斜率.……6分
设的方程为.
由消去并化简得.
设,,,.…………7分
因为,所以.
.所以.
此时,
故所求直线的方程为,或.……………10分
(未验证扣1分)
25.(本题满分10分)
解:(I)
…………2分
由已知,
得a =1 …………4分
(II)时,
函数的图象在点处的切线的方程为:
直线与函数的图象相切于点,
又,所以切线的斜率为
故切线的方程为
即的方程为:
得 …………7分
A.11
B.10
C.8
D.7
y
x1 x2 x3 x4 x
O
A
B
C
P
2
2
晕机 不晕机 合计
男乘客 28 28 56
女乘客 28 56 84
合计 56 84 140
表2
表1
同课章节目录
