湖南省蓝山二中2011-2012学年高二上学期期末考试数学(理)试题
文档属性
| 名称 | 湖南省蓝山二中2011-2012学年高二上学期期末考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 145.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-13 14:48:10 | ||
图片预览



文档简介
总分:100分 时量:120分钟
一、选择题(每题3分,共45分)
1.x>2是的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 既充分又必要条件 D. 既不充分又不必要条件
2.抛物线在点M(,)处的切线的倾斜角是( )
A.30° B.45° C.60° D.90°
3.计算机执行下面的程序段后,输出的结果是( )
A. B. C. D.
4.下列值等于1的是( )
A. B. C. D.
5.若=(2,-3,1),=(2,0,3),=(0,2,2),则(+)=( )
A. 4 B. 15 C. 7 D. 3
6.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是 ( )
A.3.5 B.-3 C.3 D.-0.5
7.在空间直角坐标系中,若向量= ( -2,1,3 ),= (1,-1,1 ),= ( 1,-,-)
则它们之间的关系是 ( )
A. 且// B. 且
C.// 且 D. //且//
8. 已知函数在处的导数为3,则的解析式可能为 ( )
A. B. C. D.
9.抛物线上一点M到焦点的距离为1,则点M的纵坐标是( )
A. B. C. D.
10. 在第1、3、4、5、8路公共汽车都要停靠的一个站(假定这个站一次只能停靠一辆汽车),有一位乘客在等候第4路或第8路公共汽车.假定当时各路汽车首先到此站的可能性相等,则首先到站正好是这位乘客所需乘的汽车的概率等于( )
A. B. C. D.
11.有一个由奇数组成的数列1,3,5,7,9,┅,现在进行如下分组:第一组含一个数,第二组含两个数,第三组含三个数,第四组含四个数,┅,经观察,可以猜想每组内各数之和与其组的编号数的关系为( )
A.等于 B.等于 C.等于 D.等于
12. 已知则以为邻边的平行四边形的面积为( )
A. B. C.4 D.8
13.给出以下命题: ⑴若,则f(x)>0; ⑵;
⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则;
其中正确命题的个数为( )
A、1 B、2 C、3 D、0
14.已知双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线的右支有且仅有一个交点,则此双曲线离心率的范围是 ( )
A . B. C. D.
15.内接于半径为R的半圆且周长最大的矩形的边长为( )
A.和 B.和 C.和 D.和
二、填空题(每题3分,共15分)
16.甲乙两人下棋比赛,两人下成和棋的概率是,乙获胜的概率是,则乙不输的概率是
17. 三棱柱中,M、N分别是、的中点,设,,,则等于
18. 已知函数,则它的单调递增区间是
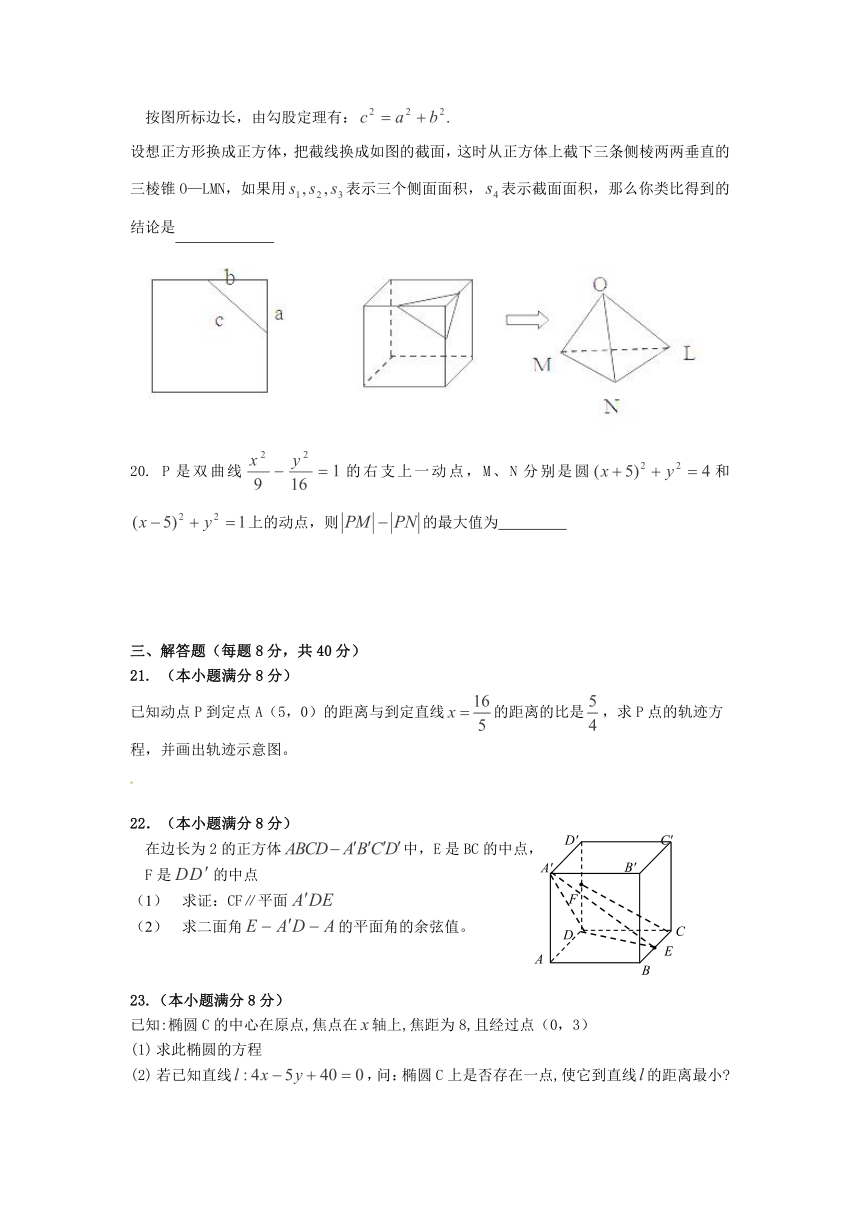
19.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,
按图所标边长,由勾股定理有:
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用表示三个侧面面积,表示截面面积,那么你类比得到的结论是
20. P是双曲线的右支上一动点,M、N分别是圆和上的动点,则的最大值为
三、解答题(每题8分,共40分)
21. (本小题满分8分)
已知动点P到定点A(5,0)的距离与到定直线的距离的比是,求P点的轨迹方
程,并画出轨迹示意图。
22.(本小题满分8分)
在边长为2的正方体中,E是BC的中点,
F是的中点
求证:CF∥平面
求二面角的平面角的余弦值。
23.(本小题满分8分)
已知:椭圆C的中心在原点,焦点在轴上,焦距为8,且经过点(0,3)
求此椭圆的方程
若已知直线,问:椭圆C上是否存在一点,使它到直线的距离最小 最小距离是多少
24.(本小题满分8分)
一艘小船在航行中的燃料费和它的速度的立方成正比。已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元。问:此船以多大的速度航行时,能使每公里的费用最少?
25.(本题满分8分)
已知函数在上为增函数,函数在上为减函数.
(1)分别求出函数和的导函数;
(2)求实数的值;
(3)求证:当时,
高二数学(理)参考答案
一、选择题(每题3分,共45分)
1.x>2是的 ( A )
A. 充分不必要条件 B. 必要不充分条件
C. 既充分又必要条件 D. 既不充分又不必要条件
2.抛物线在点M(,)处的切线的倾斜角是( B )
A.30° B.45° C.60° D.90°
3.计算机执行下面的程序段后,输出的结果是( B )
A. B. C. D.
4.下列值等于1的是 (C )
A. B. C. D.
5.若=(2,-3,1),=(2,0,3),=(0,2,2),则(+)=( D )
A. 4 B. 15 C. 7 D. 3
6.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是 ( B )
A.3.5 B.-3 C.3 D.-0.5
7.在空间直角坐标系中,若向量= ( -2,1,3 ),= (1,-1,1 ),= ( 1,-,-)
则它们之间的关系是 ( A )
A. 且// B. 且
C.// 且 D. //且//
8. 已知函数在处的导数为3,则的解析式可能为 ( A )
A.(x-1)3+3(x-1) B.2(x-1)2 C.2(x-1) D.x-1
9.抛物线上一点M到焦点的距离为1,则点M的纵坐标是( B )
A. B. C. D.
10. 在第1、3、4、5、8路公共汽车都要停靠的一个站(假定这个站一次只能停靠一辆汽车),有一位乘客在等候第4路或第8路公共汽车.假定当时各路汽车首先到此站的可能性相等,则首先到站正好是这位乘客所需乘的汽车的概率等于( D )
A. B. C. D.
11.有一个由奇数组成的数列1,3,5,7,9,┅,现在进行如下分组:第一组含一个数,第二组含两个数,第三组含三个数,第四组含四个数,┅,经观察,可以猜想每组内各数之和与其组的编号数的关系为( B )
A.等于 B.等于 C.等于 D.等于
12. 已知则以为邻边的平行四边形的面积为( A )
A. B. C.4 D.8
13.给出以下命题: ⑴若,则f(x)>0; ⑵;
⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则;
其中正确命题的个数为( B )
A、1 B、2 C、3 D、0
14.已知双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线的右支
有且仅有一个交点,则此双曲线离心率的范围是 ( C )
A . B. C. D.
15.内接于半径为R的半圆且周长最大的矩形的边长为( D )
A.和 B.和 C.和 D.和
二、填空题(每题3分,共15分)
16.甲乙两人下棋比赛,两人下成和棋的概率是,乙获胜的概率是,则乙不输的概率是
17. 三棱柱中,M、N分别是、的中点,设,,,则等于
18. 已知函数,则它的单调递增区间是和
19.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,
按图所标边长,由勾股定理有: ( http: / / www.21cnjy.com / )设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用表示三个侧面面积,表示截面面积,那么你类比得到的结论是
20. P是双曲线的右支上一动点,M、N分别是圆和上的动点,则的最大值为 9
三、解答题(每题8分,共40分)
21. (本小题满分8分)
已知动点P到定点A(5,0)的距离与到定直线的距离的比是,求P点的轨迹方
程,并画出轨迹示意图。
解:轨迹方程是 ………………6分
图略 ………………8分
22.(本小题满分8分)
在边长为2的正方体中,E是BC的中点,F是的中点
求证:CF∥平面
求二面角的平面角的余弦值。
解:分别以,, 为x轴,y轴,z轴
建立空间直角坐标系,
则(2,0,2),E(1,2,0),
D(0,0,0), C(0,2,0), F(0,0,1), ………2分
则
设平面的法向量是
则, 取………4分
,,所以,CF∥平面。…6分
(2)是面的法向量
………………8分
23.(本小题满分8分)
已知:椭圆C的中心在原点,焦点在轴上,焦距为8,且经过点(0,3)
求此椭圆的方程
若已知直线,问:椭圆C上是否存在一点,使它到直线的距离最小 最小距离是多少
解:(1) ……………4分
(2)由直线的方程与椭圆的方程可以知道,直线与椭圆不相交
设直线平行于直线,则直线的方程可以写成 (1)
由方程组
消去,得 (2)
令方程(2)的根的判别式,得 (3)
解方程(3)得或,
由图可知,当时,直线与椭圆交点到直线的距离最近,此时直线的方程为
直线与直线间的距离
所以,最小距离是. ………………8分
24.(本小题满分8分)
一艘小船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问:此船以多大的速度航行时,能使每公里的费用最少?
解:设船速度为x公里/小时(x>0)时,燃料费用Q为元,则
………………2分
………………4分
;
增。
∴当x=20时,y取得最小值。
∴此轮船以20公里/小时的速度行驶时每公里的费用总和最小。………8分
25.(本题满分8分)
已知函数在上为增函数,函数在上为减函数.
(1)分别求出函数和的导函数;
(2)求实数的值;
(3)求证:当时,
当x>0时, 1+>1,
所以由(1)知:f(1+)>f(1),即:ln(1+)+ >1,化简得:(1+x)ln(1+)>1
g(1+)所以当x>0时,xln(1+)<1<(x+1)ln(1+). ………………8分
PRINT ,
A
B
C
D
D'
C'
B'
A'
F
E
PRINT ,
b
c
a
L
N
M
O
A
B
C
D
D'
C'
B'
A'
F
E
一、选择题(每题3分,共45分)
1.x>2是的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 既充分又必要条件 D. 既不充分又不必要条件
2.抛物线在点M(,)处的切线的倾斜角是( )
A.30° B.45° C.60° D.90°
3.计算机执行下面的程序段后,输出的结果是( )
A. B. C. D.
4.下列值等于1的是( )
A. B. C. D.
5.若=(2,-3,1),=(2,0,3),=(0,2,2),则(+)=( )
A. 4 B. 15 C. 7 D. 3
6.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是 ( )
A.3.5 B.-3 C.3 D.-0.5
7.在空间直角坐标系中,若向量= ( -2,1,3 ),= (1,-1,1 ),= ( 1,-,-)
则它们之间的关系是 ( )
A. 且// B. 且
C.// 且 D. //且//
8. 已知函数在处的导数为3,则的解析式可能为 ( )
A. B. C. D.
9.抛物线上一点M到焦点的距离为1,则点M的纵坐标是( )
A. B. C. D.
10. 在第1、3、4、5、8路公共汽车都要停靠的一个站(假定这个站一次只能停靠一辆汽车),有一位乘客在等候第4路或第8路公共汽车.假定当时各路汽车首先到此站的可能性相等,则首先到站正好是这位乘客所需乘的汽车的概率等于( )
A. B. C. D.
11.有一个由奇数组成的数列1,3,5,7,9,┅,现在进行如下分组:第一组含一个数,第二组含两个数,第三组含三个数,第四组含四个数,┅,经观察,可以猜想每组内各数之和与其组的编号数的关系为( )
A.等于 B.等于 C.等于 D.等于
12. 已知则以为邻边的平行四边形的面积为( )
A. B. C.4 D.8
13.给出以下命题: ⑴若,则f(x)>0; ⑵;
⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则;
其中正确命题的个数为( )
A、1 B、2 C、3 D、0
14.已知双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线的右支有且仅有一个交点,则此双曲线离心率的范围是 ( )
A . B. C. D.
15.内接于半径为R的半圆且周长最大的矩形的边长为( )
A.和 B.和 C.和 D.和
二、填空题(每题3分,共15分)
16.甲乙两人下棋比赛,两人下成和棋的概率是,乙获胜的概率是,则乙不输的概率是
17. 三棱柱中,M、N分别是、的中点,设,,,则等于
18. 已知函数,则它的单调递增区间是
19.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,
按图所标边长,由勾股定理有:
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用表示三个侧面面积,表示截面面积,那么你类比得到的结论是
20. P是双曲线的右支上一动点,M、N分别是圆和上的动点,则的最大值为
三、解答题(每题8分,共40分)
21. (本小题满分8分)
已知动点P到定点A(5,0)的距离与到定直线的距离的比是,求P点的轨迹方
程,并画出轨迹示意图。
22.(本小题满分8分)
在边长为2的正方体中,E是BC的中点,
F是的中点
求证:CF∥平面
求二面角的平面角的余弦值。
23.(本小题满分8分)
已知:椭圆C的中心在原点,焦点在轴上,焦距为8,且经过点(0,3)
求此椭圆的方程
若已知直线,问:椭圆C上是否存在一点,使它到直线的距离最小 最小距离是多少
24.(本小题满分8分)
一艘小船在航行中的燃料费和它的速度的立方成正比。已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元。问:此船以多大的速度航行时,能使每公里的费用最少?
25.(本题满分8分)
已知函数在上为增函数,函数在上为减函数.
(1)分别求出函数和的导函数;
(2)求实数的值;
(3)求证:当时,
高二数学(理)参考答案
一、选择题(每题3分,共45分)
1.x>2是的 ( A )
A. 充分不必要条件 B. 必要不充分条件
C. 既充分又必要条件 D. 既不充分又不必要条件
2.抛物线在点M(,)处的切线的倾斜角是( B )
A.30° B.45° C.60° D.90°
3.计算机执行下面的程序段后,输出的结果是( B )
A. B. C. D.
4.下列值等于1的是 (C )
A. B. C. D.
5.若=(2,-3,1),=(2,0,3),=(0,2,2),则(+)=( D )
A. 4 B. 15 C. 7 D. 3
6.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是 ( B )
A.3.5 B.-3 C.3 D.-0.5
7.在空间直角坐标系中,若向量= ( -2,1,3 ),= (1,-1,1 ),= ( 1,-,-)
则它们之间的关系是 ( A )
A. 且// B. 且
C.// 且 D. //且//
8. 已知函数在处的导数为3,则的解析式可能为 ( A )
A.(x-1)3+3(x-1) B.2(x-1)2 C.2(x-1) D.x-1
9.抛物线上一点M到焦点的距离为1,则点M的纵坐标是( B )
A. B. C. D.
10. 在第1、3、4、5、8路公共汽车都要停靠的一个站(假定这个站一次只能停靠一辆汽车),有一位乘客在等候第4路或第8路公共汽车.假定当时各路汽车首先到此站的可能性相等,则首先到站正好是这位乘客所需乘的汽车的概率等于( D )
A. B. C. D.
11.有一个由奇数组成的数列1,3,5,7,9,┅,现在进行如下分组:第一组含一个数,第二组含两个数,第三组含三个数,第四组含四个数,┅,经观察,可以猜想每组内各数之和与其组的编号数的关系为( B )
A.等于 B.等于 C.等于 D.等于
12. 已知则以为邻边的平行四边形的面积为( A )
A. B. C.4 D.8
13.给出以下命题: ⑴若,则f(x)>0; ⑵;
⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则;
其中正确命题的个数为( B )
A、1 B、2 C、3 D、0
14.已知双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线的右支
有且仅有一个交点,则此双曲线离心率的范围是 ( C )
A . B. C. D.
15.内接于半径为R的半圆且周长最大的矩形的边长为( D )
A.和 B.和 C.和 D.和
二、填空题(每题3分,共15分)
16.甲乙两人下棋比赛,两人下成和棋的概率是,乙获胜的概率是,则乙不输的概率是
17. 三棱柱中,M、N分别是、的中点,设,,,则等于
18. 已知函数,则它的单调递增区间是和
19.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,
按图所标边长,由勾股定理有: ( http: / / www.21cnjy.com / )设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用表示三个侧面面积,表示截面面积,那么你类比得到的结论是
20. P是双曲线的右支上一动点,M、N分别是圆和上的动点,则的最大值为 9
三、解答题(每题8分,共40分)
21. (本小题满分8分)
已知动点P到定点A(5,0)的距离与到定直线的距离的比是,求P点的轨迹方
程,并画出轨迹示意图。
解:轨迹方程是 ………………6分
图略 ………………8分
22.(本小题满分8分)
在边长为2的正方体中,E是BC的中点,F是的中点
求证:CF∥平面
求二面角的平面角的余弦值。
解:分别以,, 为x轴,y轴,z轴
建立空间直角坐标系,
则(2,0,2),E(1,2,0),
D(0,0,0), C(0,2,0), F(0,0,1), ………2分
则
设平面的法向量是
则, 取………4分
,,所以,CF∥平面。…6分
(2)是面的法向量
………………8分
23.(本小题满分8分)
已知:椭圆C的中心在原点,焦点在轴上,焦距为8,且经过点(0,3)
求此椭圆的方程
若已知直线,问:椭圆C上是否存在一点,使它到直线的距离最小 最小距离是多少
解:(1) ……………4分
(2)由直线的方程与椭圆的方程可以知道,直线与椭圆不相交
设直线平行于直线,则直线的方程可以写成 (1)
由方程组
消去,得 (2)
令方程(2)的根的判别式,得 (3)
解方程(3)得或,
由图可知,当时,直线与椭圆交点到直线的距离最近,此时直线的方程为
直线与直线间的距离
所以,最小距离是. ………………8分
24.(本小题满分8分)
一艘小船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问:此船以多大的速度航行时,能使每公里的费用最少?
解:设船速度为x公里/小时(x>0)时,燃料费用Q为元,则
………………2分
………………4分
;
增。
∴当x=20时,y取得最小值。
∴此轮船以20公里/小时的速度行驶时每公里的费用总和最小。………8分
25.(本题满分8分)
已知函数在上为增函数,函数在上为减函数.
(1)分别求出函数和的导函数;
(2)求实数的值;
(3)求证:当时,
当x>0时, 1+>1,
所以由(1)知:f(1+)>f(1),即:ln(1+)+ >1,化简得:(1+x)ln(1+)>1
g(1+)
PRINT ,
A
B
C
D
D'
C'
B'
A'
F
E
PRINT ,
b
c
a
L
N
M
O
A
B
C
D
D'
C'
B'
A'
F
E
同课章节目录
