湖南省蓝山二中2012届高三第六次联考数学(文)试题
文档属性
| 名称 | 湖南省蓝山二中2012届高三第六次联考数学(文)试题 | 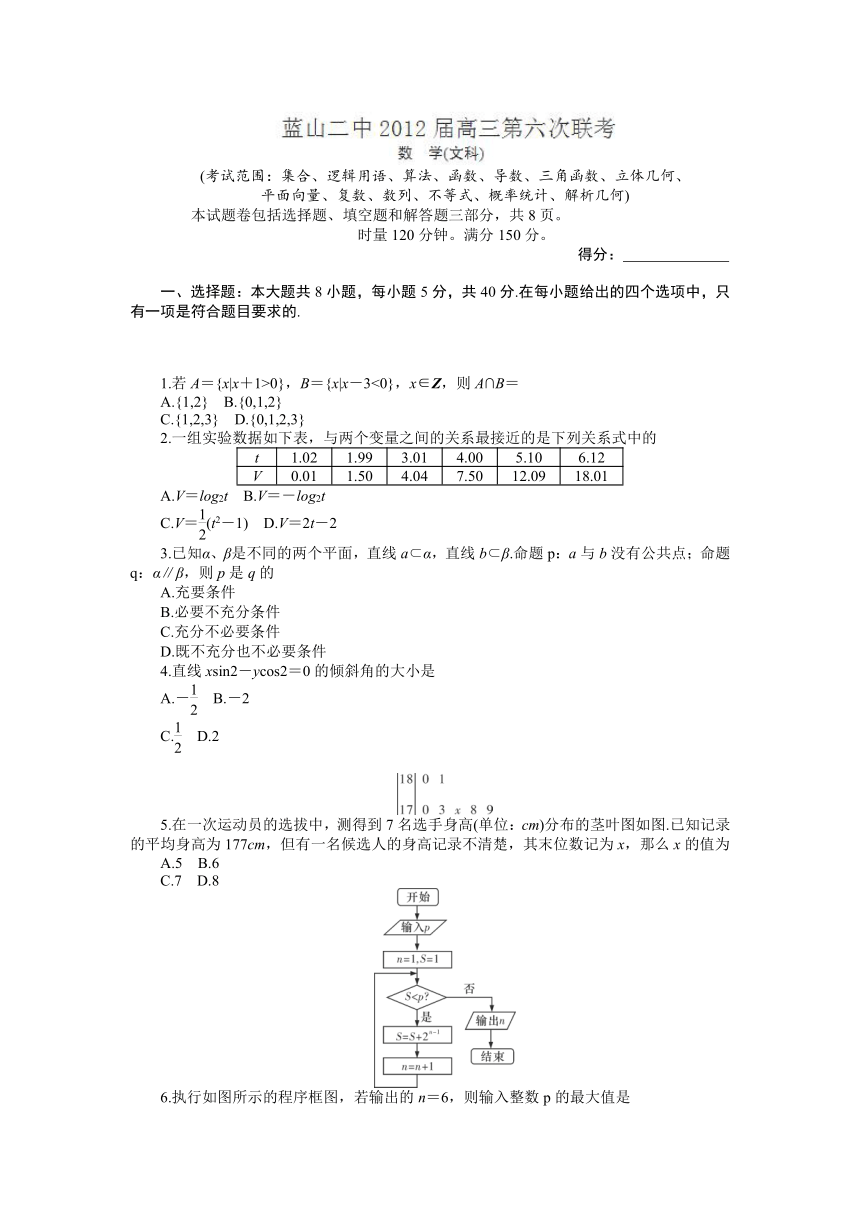 | |
| 格式 | zip | ||
| 文件大小 | 74.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-13 14:48:10 | ||
图片预览




文档简介
(考试范围:集合、逻辑用语、算法、函数、导数、三角函数、立体几何、
平面向量、复数、数列、不等式、概率统计、解析几何)
本试题卷包括选择题、填空题和解答题三部分,共8页。
时量120分钟。满分150分。
得分:
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若A={x|x+1>0},B={x|x-3<0},x∈Z,则A∩B=
A.{1,2} B.{0,1,2}
C.{1,2,3} D.{0,1,2,3}
2.一组实验数据如下表,与两个变量之间的关系最接近的是下列关系式中的
t 1.02 1.99 3.01 4.00 5.10 6.12
V 0.01 1.50 4.04 7.50 12.09 18.01
A.V=log2t B.V=-log2t
C.V=(t2-1) D.V=2t-2
3.已知α、β是不同的两个平面,直线a α,直线b β.命题p:a与b没有公共点;命题q:α∥β,则p是q的
A.充要条件
B.必要不充分条件
C.充分不必要条件
D.既不充分也不必要条件
4.直线xsin2-ycos2=0的倾斜角的大小是
A.- B.-2
C. D.2
5.在一次运动员的选拔中,测得到7名选手身高(单位:cm)分布的茎叶图如图.已知记录的平均身高为177cm,但有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为
A.5 B.6
C.7 D.8
6.执行如图所示的程序框图,若输出的n=6,则输入整数p的最大值是
A.32 B.31
C.15 D.16
7.设双曲线- =1(a>0,b>0)的离心率为,抛物线y2=20x的准线过双曲线的左焦点,则此双曲线的方程为
A.-=1 B.-=1
C.-=1 D.-=1
8.已知实系数一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1、x2,满足02.则的取值范围是
A.(-1,-) B.(-3,-1)
C.(-3,-) D.(-3,)
选择题答题卡
题 号 1 2 3 4 5 6 7 8
答 案
二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答题卡中对应题号后的横线上.
9.sin45°cos15°+cos45°sin15°的值为 .
10.若=ad-bc,则复数= .
11.函数y=2cos2-1的最小正周期是 .
12.若直线l:y+1=k(x-2)被圆C:x2+y2-2x-24=0截得的弦AB最短,则直线AB的方程是 .
13.有一个底面圆半径为1、高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,则点P到点O的距离大于1的概率为 .
14.已知向量a=(3,4),|a-b|=1,则|b|的范围是 .
15.某同学在研究函数f(x)=(x∈R)时,分别给出下面几个结论:
①等式f(-x)+f(x)=0对x∈R恒成立;
②函数f(x)的值域为(-1,1);
③若x1≠x2,则一定有f(x1)≠f(x2);
④函数g(x)=f(x)-x在R上有三个零点.
其中正确结论的序号有 .(请将你认为正确的结论的序号都填上)
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
在△ABC中,角A、B、C的对应边分别为a,b,c,且满足a2-ab+b2=c2.
(1)求角C;
(2)若△ABC的面积为,c=2,求a+b的值.
17.(本小题满分12分)
如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,E、M分别是DC、BC的中点.
(1)证明:AM⊥面PME;
(2)求二面角P—AM—D的大小.
18.(本小题满分12分)
已知:△ABC为直角三角形,∠C为直角,A(0,-8),顶点C在x轴上运动,M在y轴上,=(+),设B的运动轨迹为曲线E.
(1)求B的运动轨迹曲线E的方程;
(2)过点P(2,4)的直线l与曲线E相交于不同的两点Q、N,且满足=,求直线l的方程.
19.(本小题满分13分)
统计某校高三年级100名学生的数学月考成绩,得到样本频率分布直方图如下图所示,已知前4组的频数分别是等比数列的前4项,后6组的频数分别是等差数列的前6项,
(1)求数列、的通项公式;
(2)设m、n为该校学生的数学月考成绩,且已知m、n∈∪,求事件“>10”的概率.
20.(本小题满分13分)
为了加快经济的发展,某省选择A、B两城市作为龙头带动周边城市的发展,决定在A、B两城市的周边修建城际轻轨,假设10km为一个单位距离,A、B两城市相距8个单位距离,设城际轻轨所在的曲线为E,使轻轨E上的点到A、B两市的距离之和为10个单位距离,
(1)建立如图的直角坐标系,求城际轻轨所在曲线E的方程;
(2)若要在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离,求M、N之间的距离有多少个单位距离?
(3)在A、B两城市之间有一条与AB所在直线成45°的笔直公路l,直线l与曲线E交于P,Q两点,求四边形PAQB的面积的最大值.
21.(本小题满分13分)
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M,都有f(x)≥M成立,则称f是D上的有界函数,其中M称为函数f的下界.已知函数f(x)=(x2-3x+3)·ex,其定义域为[-2,t](t>-2),设f(-2)=m,f(t)=n.
(1)试确定t的取值范围,使得函数f(x)在[-2,t]上为单调递增函数;
(2)试判断m,n的大小,并说明理由;并判断函数f在定义域上是否为有界函数,请说明理由;
(3)求证:对于任意的t>-2,总存在x0∈(-2,t)满足=(t-1)2,并确定这样的x0的个数.
文科数学参考答案
一、选择题
题 号 1 2 3 4 5 6 7 8
答 案 B C B D D A C C
二、填空题
9. 10.3+i 11.2π 12.x-y-3=0 13. 14.[4,6] 15.①②③
三、解答题
17.解:(1)连接EA,∵△PCD为正三角形,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD,∴PE⊥AM.(3分)
∵四边形ABCD是矩形,∴△ADE、△ECM、△ABM均为直角三角形,由勾股定理可求得
EM=,AM=,AE=3,∴EM2+AM2=AE2,∴∠AME=90°,∴AM⊥EM.(4分)
又EM∩PE=E,∴AM⊥面PME.(6分)
(2)∵AM⊥平面PME,∴PM⊥AM,∴∠PME是二面角P—AM—D的平面角,
PE=PDsin60°=,∴tan∠PME===1,∴∠PME=45°,
∴二面角P—AM—D为45°.(12分)
18.解:(1)由=(+),知M为BC中点,(2分)
设B(x,y)则M(0,),C(-x,0).(4分)
又∠C为直角,故·=0,∴x2=4y(5分)
B的运动轨迹曲线E的方程为x2=4y.(x≠0)(6分)
(2)∵=,∴点P是线段QN的中点,
设Q(x1,y1)、N(x2,y2),线段QN的中点P(2,4),设l:y-4=k(x-2)
方法一:则x=4y1,① x=4y2,②
①-②得:4y1-4y2=(x1-x2)(x1+x2),(8分)
∴直线l的斜率为k==(x1+x2)=1.(11分)
方法二:由
x2=4y)),消去y得x2-4kx+8k-16=0,(*)
方程(*)中Δ=16(k2-2k+4)>0,显然方程(*)有两个不相等的实数根.(8分)
由x1+x2=4k=4 k=1.(11分)
所以直线l的方程为x-y+2=0.(12分)
19.解:(1)由已知:第2组的频数为3,第3组的频数为9,又前4组的频数是等比数列,
所以an=3n-1,(3分)
又第4组的频数为27,后6组是首项为27,和是87的等差数列,
所以bn=-5n+32.(6分)
(2)由(1)知成绩在中的有3人,成绩在中的有2人,分别记为:a1,a2,a3和b1,b2,由>10知,这两人必来自两个不同的组,(8分)
所以事件“>10”的概率为.(13分)
20.解:(1)以AB为x轴,以AB中点为原点O建立直角坐标系.设曲线E上点P(x,y),
∵|PA|+|PB|=10>=8
∴动点轨迹为椭圆,且a=5,c=4,从而b=3.
∴曲线E的方程为+=1.(4分)
(2)由|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,所以|MN|=8.(8分)
(3)将y=x+t代入+=1,得34y2-18ty+9t2-25×9=0.
设P(x1,y1)、Q(x2,y2),则y1+y2=,y1y2=.
==,
S=S△ABP+S△ABQ=AB·=,
所以当t=0时,面积最大是,此时直线为l:y=x.(13分)
21.解:(1)f′(x)=(x2-3x+3)·ex+(2x-3)·ex=x(x-1)·ex.
由f′(x)>0 x>1或x<0;由f′(x)<0 0所以f(x)在(-∞,0],[1,+∞)上单调递增,在[0,1]上单调递减,
要使f(x)在[-2,t]上为单调递增函数,则-2(2)n>m.
因为f(x)在(-∞,0],[1,+∞)上单调递增,在[0,1]上单调递减,
所以f(x)在x=1处取极小值e.又f(-2)=所以f(x)在[-2,+∞)上的最小值为f(-2),从而当t>-2时,f(-2)即m由上知,因为f(x)在上递增,且恒大于0,f(x)在(0,+∞)的最小值为e,
所以函数f在(-∞,+∞)上是有界函数,M=0.(8分)
(3)因为=x-x0,所以=(t-1)2,即为x-x0=(t-1)2.
令g(x)=x2-x-(t-1)2,从而问题转化为证明方程g(x)=x2-x-(t-1)2=0
在(-2,t)上有解,并讨论解的个数.
因为g(-2)=6-(t-1)2=-(t+2)(t-4),g(t)=t(t-1)-(t-1)2=(t+2)(t-1),
所以①当t>4或-2
平面向量、复数、数列、不等式、概率统计、解析几何)
本试题卷包括选择题、填空题和解答题三部分,共8页。
时量120分钟。满分150分。
得分:
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若A={x|x+1>0},B={x|x-3<0},x∈Z,则A∩B=
A.{1,2} B.{0,1,2}
C.{1,2,3} D.{0,1,2,3}
2.一组实验数据如下表,与两个变量之间的关系最接近的是下列关系式中的
t 1.02 1.99 3.01 4.00 5.10 6.12
V 0.01 1.50 4.04 7.50 12.09 18.01
A.V=log2t B.V=-log2t
C.V=(t2-1) D.V=2t-2
3.已知α、β是不同的两个平面,直线a α,直线b β.命题p:a与b没有公共点;命题q:α∥β,则p是q的
A.充要条件
B.必要不充分条件
C.充分不必要条件
D.既不充分也不必要条件
4.直线xsin2-ycos2=0的倾斜角的大小是
A.- B.-2
C. D.2
5.在一次运动员的选拔中,测得到7名选手身高(单位:cm)分布的茎叶图如图.已知记录的平均身高为177cm,但有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为
A.5 B.6
C.7 D.8
6.执行如图所示的程序框图,若输出的n=6,则输入整数p的最大值是
A.32 B.31
C.15 D.16
7.设双曲线- =1(a>0,b>0)的离心率为,抛物线y2=20x的准线过双曲线的左焦点,则此双曲线的方程为
A.-=1 B.-=1
C.-=1 D.-=1
8.已知实系数一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1、x2,满足0
A.(-1,-) B.(-3,-1)
C.(-3,-) D.(-3,)
选择题答题卡
题 号 1 2 3 4 5 6 7 8
答 案
二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答题卡中对应题号后的横线上.
9.sin45°cos15°+cos45°sin15°的值为 .
10.若=ad-bc,则复数= .
11.函数y=2cos2-1的最小正周期是 .
12.若直线l:y+1=k(x-2)被圆C:x2+y2-2x-24=0截得的弦AB最短,则直线AB的方程是 .
13.有一个底面圆半径为1、高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,则点P到点O的距离大于1的概率为 .
14.已知向量a=(3,4),|a-b|=1,则|b|的范围是 .
15.某同学在研究函数f(x)=(x∈R)时,分别给出下面几个结论:
①等式f(-x)+f(x)=0对x∈R恒成立;
②函数f(x)的值域为(-1,1);
③若x1≠x2,则一定有f(x1)≠f(x2);
④函数g(x)=f(x)-x在R上有三个零点.
其中正确结论的序号有 .(请将你认为正确的结论的序号都填上)
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
在△ABC中,角A、B、C的对应边分别为a,b,c,且满足a2-ab+b2=c2.
(1)求角C;
(2)若△ABC的面积为,c=2,求a+b的值.
17.(本小题满分12分)
如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,E、M分别是DC、BC的中点.
(1)证明:AM⊥面PME;
(2)求二面角P—AM—D的大小.
18.(本小题满分12分)
已知:△ABC为直角三角形,∠C为直角,A(0,-8),顶点C在x轴上运动,M在y轴上,=(+),设B的运动轨迹为曲线E.
(1)求B的运动轨迹曲线E的方程;
(2)过点P(2,4)的直线l与曲线E相交于不同的两点Q、N,且满足=,求直线l的方程.
19.(本小题满分13分)
统计某校高三年级100名学生的数学月考成绩,得到样本频率分布直方图如下图所示,已知前4组的频数分别是等比数列的前4项,后6组的频数分别是等差数列的前6项,
(1)求数列、的通项公式;
(2)设m、n为该校学生的数学月考成绩,且已知m、n∈∪,求事件“>10”的概率.
20.(本小题满分13分)
为了加快经济的发展,某省选择A、B两城市作为龙头带动周边城市的发展,决定在A、B两城市的周边修建城际轻轨,假设10km为一个单位距离,A、B两城市相距8个单位距离,设城际轻轨所在的曲线为E,使轻轨E上的点到A、B两市的距离之和为10个单位距离,
(1)建立如图的直角坐标系,求城际轻轨所在曲线E的方程;
(2)若要在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离,求M、N之间的距离有多少个单位距离?
(3)在A、B两城市之间有一条与AB所在直线成45°的笔直公路l,直线l与曲线E交于P,Q两点,求四边形PAQB的面积的最大值.
21.(本小题满分13分)
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M,都有f(x)≥M成立,则称f是D上的有界函数,其中M称为函数f的下界.已知函数f(x)=(x2-3x+3)·ex,其定义域为[-2,t](t>-2),设f(-2)=m,f(t)=n.
(1)试确定t的取值范围,使得函数f(x)在[-2,t]上为单调递增函数;
(2)试判断m,n的大小,并说明理由;并判断函数f在定义域上是否为有界函数,请说明理由;
(3)求证:对于任意的t>-2,总存在x0∈(-2,t)满足=(t-1)2,并确定这样的x0的个数.
文科数学参考答案
一、选择题
题 号 1 2 3 4 5 6 7 8
答 案 B C B D D A C C
二、填空题
9. 10.3+i 11.2π 12.x-y-3=0 13. 14.[4,6] 15.①②③
三、解答题
17.解:(1)连接EA,∵△PCD为正三角形,∴PE⊥CD,
∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD,∴PE⊥AM.(3分)
∵四边形ABCD是矩形,∴△ADE、△ECM、△ABM均为直角三角形,由勾股定理可求得
EM=,AM=,AE=3,∴EM2+AM2=AE2,∴∠AME=90°,∴AM⊥EM.(4分)
又EM∩PE=E,∴AM⊥面PME.(6分)
(2)∵AM⊥平面PME,∴PM⊥AM,∴∠PME是二面角P—AM—D的平面角,
PE=PDsin60°=,∴tan∠PME===1,∴∠PME=45°,
∴二面角P—AM—D为45°.(12分)
18.解:(1)由=(+),知M为BC中点,(2分)
设B(x,y)则M(0,),C(-x,0).(4分)
又∠C为直角,故·=0,∴x2=4y(5分)
B的运动轨迹曲线E的方程为x2=4y.(x≠0)(6分)
(2)∵=,∴点P是线段QN的中点,
设Q(x1,y1)、N(x2,y2),线段QN的中点P(2,4),设l:y-4=k(x-2)
方法一:则x=4y1,① x=4y2,②
①-②得:4y1-4y2=(x1-x2)(x1+x2),(8分)
∴直线l的斜率为k==(x1+x2)=1.(11分)
方法二:由
x2=4y)),消去y得x2-4kx+8k-16=0,(*)
方程(*)中Δ=16(k2-2k+4)>0,显然方程(*)有两个不相等的实数根.(8分)
由x1+x2=4k=4 k=1.(11分)
所以直线l的方程为x-y+2=0.(12分)
19.解:(1)由已知:第2组的频数为3,第3组的频数为9,又前4组的频数是等比数列,
所以an=3n-1,(3分)
又第4组的频数为27,后6组是首项为27,和是87的等差数列,
所以bn=-5n+32.(6分)
(2)由(1)知成绩在中的有3人,成绩在中的有2人,分别记为:a1,a2,a3和b1,b2,由>10知,这两人必来自两个不同的组,(8分)
所以事件“>10”的概率为.(13分)
20.解:(1)以AB为x轴,以AB中点为原点O建立直角坐标系.设曲线E上点P(x,y),
∵|PA|+|PB|=10>=8
∴动点轨迹为椭圆,且a=5,c=4,从而b=3.
∴曲线E的方程为+=1.(4分)
(2)由|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,所以|MN|=8.(8分)
(3)将y=x+t代入+=1,得34y2-18ty+9t2-25×9=0.
设P(x1,y1)、Q(x2,y2),则y1+y2=,y1y2=.
==,
S=S△ABP+S△ABQ=AB·=,
所以当t=0时,面积最大是,此时直线为l:y=x.(13分)
21.解:(1)f′(x)=(x2-3x+3)·ex+(2x-3)·ex=x(x-1)·ex.
由f′(x)>0 x>1或x<0;由f′(x)<0 0
要使f(x)在[-2,t]上为单调递增函数,则-2
因为f(x)在(-∞,0],[1,+∞)上单调递增,在[0,1]上单调递减,
所以f(x)在x=1处取极小值e.又f(-2)=
所以函数f在(-∞,+∞)上是有界函数,M=0.(8分)
(3)因为=x-x0,所以=(t-1)2,即为x-x0=(t-1)2.
令g(x)=x2-x-(t-1)2,从而问题转化为证明方程g(x)=x2-x-(t-1)2=0
在(-2,t)上有解,并讨论解的个数.
因为g(-2)=6-(t-1)2=-(t+2)(t-4),g(t)=t(t-1)-(t-1)2=(t+2)(t-1),
所以①当t>4或-2
同课章节目录
