六年级下册数学试题 6.2.1 平面图形的认识与测量人教版(39张ppt)
文档属性
| 名称 | 六年级下册数学试题 6.2.1 平面图形的认识与测量人教版(39张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 10:56:08 | ||
图片预览




文档简介
平面图形的认识与测量(1)
整理和复习
6
二维图像是指不包含深度信息的平面图像。 二维即左右、上下四个方向,不存在前后。在一张纸上的内容就可以看做成是二维。也就是平时我们所说的平面图形。常应用于人脸识别技术,用摄像机或摄像头采集含有人脸的图像,并自动在图像中检测和跟踪人脸,进而对检测到的人脸进行脸部识别,通常也叫做人像识别、面部识别。
举手回答:我们学过哪些平面图形?你能对学过的图形进行分类吗?
图形都是由线组成,那么我们就从复习线开始复习几何图形。
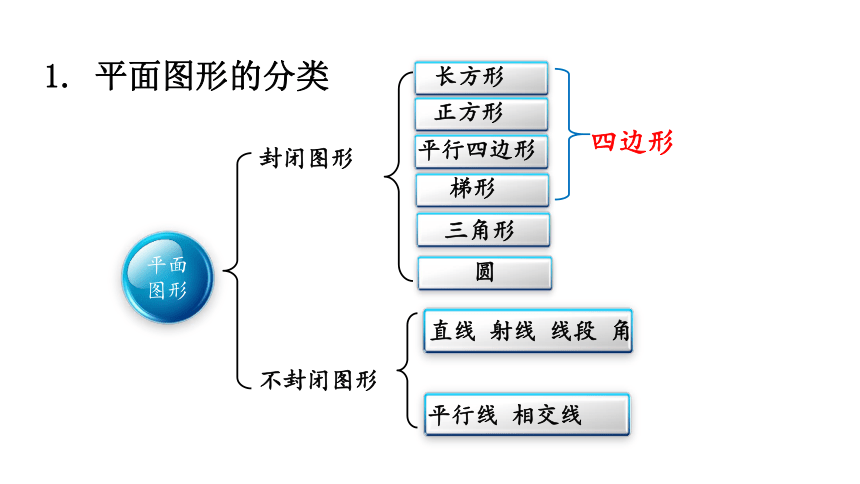
1. 平面图形的分类
封闭图形
不封闭图形
直线 射线 线段 角
平行线 相交线
四边形
平面图形
长方形
圆
正方形
平行四边形
梯形
三角形
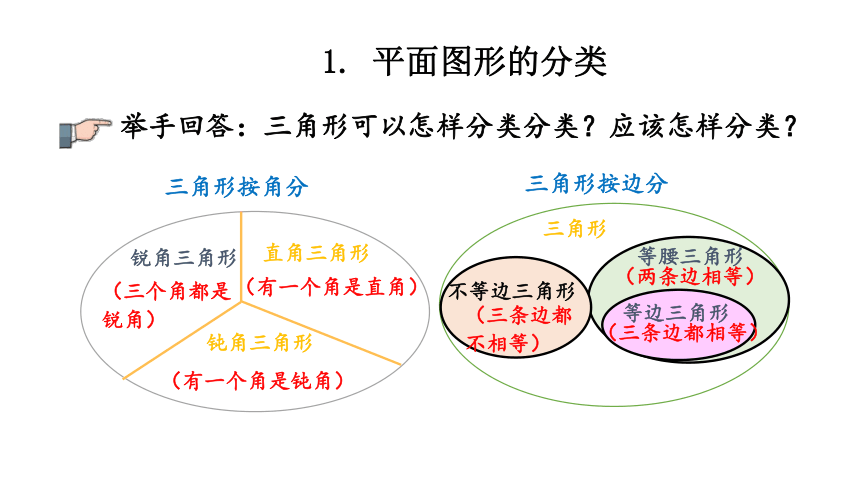
举手回答:三角形可以怎样分类分类?应该怎样分类?
1. 平面图形的分类
三角形按角分
锐角三角形
直角三角形
钝角三角形
(三个角都是锐角)
(有一个角是直角)
(有一个角是钝角)
三角形
等腰三角形
等边三角形
三角形按边分
(两条边相等)
(三条边都相等)
不等边三角形
(三条边都不相等)
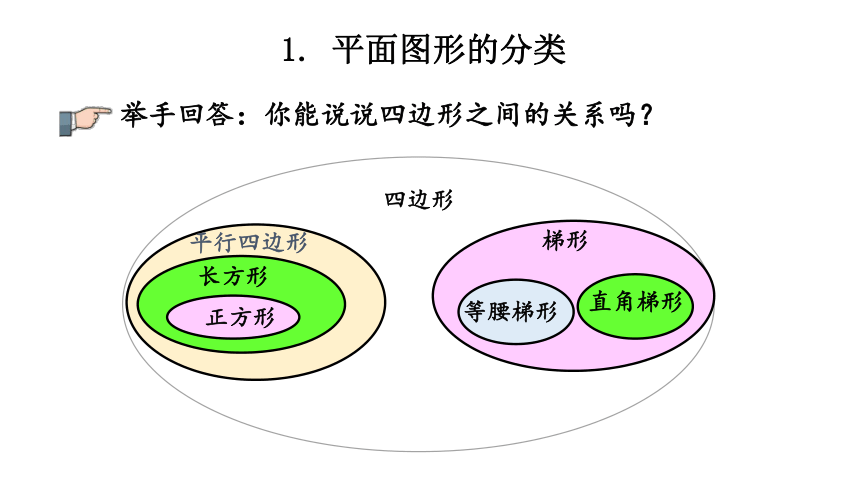
举手回答:你能说说四边形之间的关系吗?
1. 平面图形的分类
四边形
平行四边形
长方形
正方形
梯形
等腰梯形
直角梯形
2. 直线、射线和线段
射线
线段
直线
不同点
相同点
名称
能否延长
能
不能
不能
能否测量长度
1个
无
都是直
直的线
端点个数
2个
可以向两
端无限延长
可以向一
端无限延长
不能向两
端无限延长
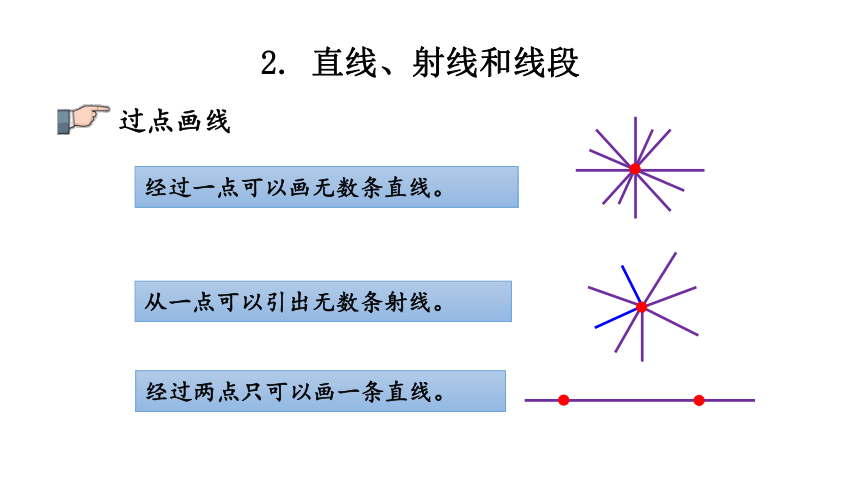
过点画线
经过一点可以画无数条直线。
从一点可以引出无数条射线。
经过两点只可以画一条直线。
2. 直线、射线和线段
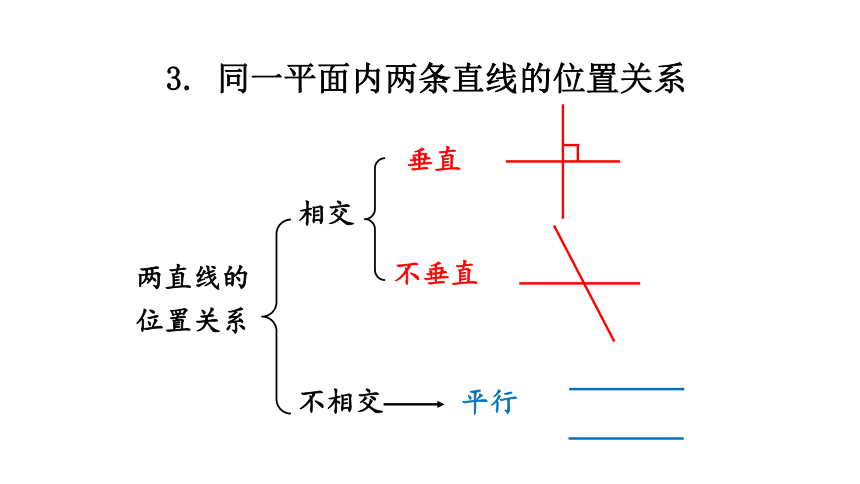
3. 同一平面内两条直线的位置关系
两直线的
位置关系
相交
不相交
垂直
不垂直
平行
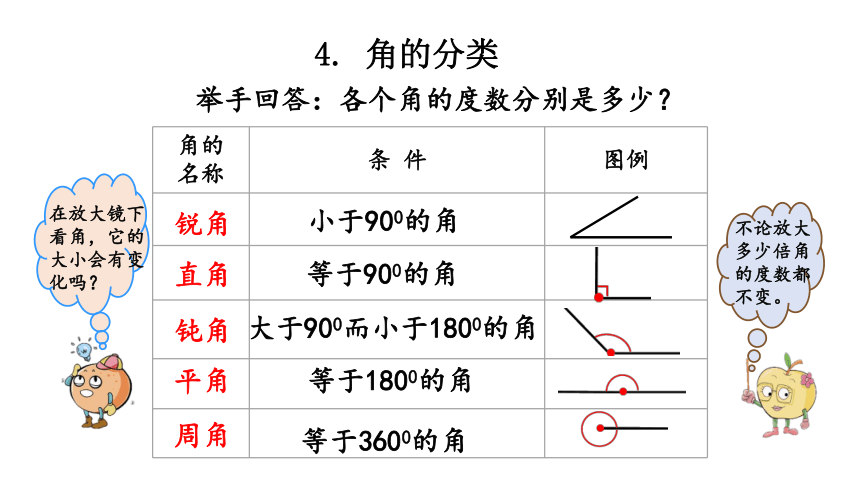
4. 角的分类
{8799B23B-EC83-4686-B30A-512413B5E67A}角的
名称
条 件
图例
锐角
小于900的角
直角
等于900的角
钝角
大于900而小于1800的角
平角
等于1800的角
周角
等于3600的角
在放大镜下看角,它的大小会有变化吗?
不论放大多少倍角的度数都不变。
举手回答:各个角的度数分别是多少?
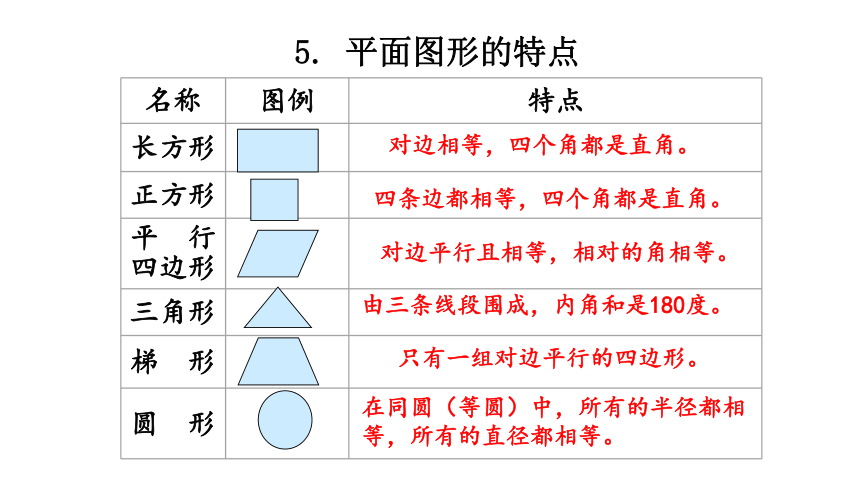
5. 平面图形的特点
{8799B23B-EC83-4686-B30A-512413B5E67A}名称
图例
特点
长方形
正方形
平 行
四边形
三角形
梯 形
圆 形
对边相等,四个角都是直角。
四条边都相等,四个角都是直角。
对边平行且相等,相对的角相等。
由三条线段围成,内角和是180度。
只有一组对边平行的四边形。
在同圆(等圆)中,所有的半径都相等,所有的直径都相等。
6. 圆
圆是平面图形上封闭的曲线图形
一个圆有无数条半径,一般用字母r表示;有无数条直径,一般用字母d表示。
1
同一个圆内,直径的长度是半径的2倍,即:d=2r。
2
3
圆是轴对称图形,它有无数条对称轴。
7.平面图形的周长和面积公式
C=2(ɑ+b)
S=ab
C=4a????
S=ɑ2
S=ɑh
C=2πr =πd
S=πr2
S=ɑh÷2
S=?(ɑ+b)h÷2
a
b
a
a
h
r
a
h
a
b
h
举手回答:我们学过哪些图形的周长与面积?说一说他们的公式分别是什么?
这些计算公式是怎样推导出来的?它们之间有什么联系?
利用割补、转化的方法来推导图形的面积公式。
长方形的面积是研究其它图形面积的基础。
长方形和正方形是用面积单位量出来的。
平行四边形转化成长方形。
两个完全相同的三角形或梯形都可以拼成平行四边形。
8.平面图形的周长和面积公式
9.三角形三边的关系
13cm
4cm
7cm
三角形其中两条线段的和大于第三条线段时,这样的三条线段才能组成一个三角形。
同桌交流:试着用自己的话说一说,三角形第三条边的取值在什么范围?
在括号里填上合适的计量单位。
北京至上海的铁路长约1463( )。
足球场的面积约为7500( )。
东北虎的体重可达320( )。
小虹家的冰箱容积有240 ( )。
km
kg
m2
L
下面说法是否正确?对的画“√”,错的画“×”。
(1)大于90°的角叫钝角。
(2)角的两条边越长,角就越大。
( )
( )
(3)直线的两端可以无限延长。
( )
(4)可以画一条长10厘米的直线。
( )
(5)平角就是一条直线。
( )
√
×
×
×
×
大于90°而小于180°
角的大小与角的两边的长短无关,与角的张口的大小有关。
只要是角,就是由一个顶点和两条边组成。
直线是不可度量。
做两个一样的平行四边形纸片。把它们重合在一起,将上面的平行四边形绕它的一个顶点旋转180度,再通过平移使它与下面的平行四边形重合。观察两个平行四边形的各条边与各个角,你有什么发现?
旋转和平移后的图形,各边与各个角都不变。
(1)请你画一条从蘑菇房到小木屋最近的路。
(2)请你画一条从蘑菇房通向小河最近的路。
动手操作。
计算下面各图形的周长和面积。(单位:m)
C:30+40+50
=120(m)
S:30×40÷2
=1200÷2
=600(m2)
C:6+6+7.5+10.5=30(m)
S:(6+10.5)×6÷2
=16.5 ×6÷2
=49.5( m2 )
C:3+5×2+3.14×5÷2+(5-2)
=15.7(m)
S:3.14×( 5÷2 )2÷2
+5 ×3
=9.8125+15
=24.8125( m2 )
如果一个正方形能够被分割为若干个边长不等的小正方形,则这个正方形成为完美正方形。下面的正方形是已知包含21个小正方形的完美正方形(称为21阶完美正方形),这个迄今为止最小阶数的完美正方形,分割方法如图所示,其中小正方形中心的数字代表其边长。请计算这个完美正方形的边长。(单位:厘米)
50+35+27=112(厘米)
答:这个正方形的周长是112厘米。
(1) 图中有( )条直线,( )条射线,( )条线段。
(2)钟面上3时整,时针和分针组成的角是( )角。
(3)一个三角形的两条边的长分别是8 cm和12 cm,第三条边最长是( ) cm,最短是( ) cm。(填整厘米数)
1.填一填。
考点
平面图形的认识
1
8
6
直
19
5
(4)一个三角形的两个角分别是78°和27°,第三个角是( )°。
(5)( )形和( )形是特殊的平行四边形,它们的对边分别( )且( )。
(6)如图,圆的半径是( )cm,长方形的周长是( ) cm,它有( )条对称轴。
75
长方
正方
平行
相等
3
30
一
2.选择。(将正确答案的字母填在括号里)
(1)把平行四边形任意分割成两个梯形,这两个梯形的
( )相等。
A.高 B.周长 C.上下底之和 D.面积
(2)下面图形中,不是轴对称图形的是( )。
A.半圆形 B.长方形
C.平行四边形 D.等腰梯形
A
C
(3)在同一平面内,与已知直线相距5 cm的直线有( )条。
A.1 B.2 C.无数 D.0
(4)一个三角形三个角的度数都不相等,其中最小的角是45°,这个三角形一定是( )三角形。
A.锐角 B.直角
C.钝角 D.等腰直角
B
A
3.判断。(对的画“√”,错的画“×”)
(1)从平行四边形的一个顶点出发最多可以画两条高。 ( )
(2)如果两个梯形能拼成一个平行四边形,那么这两个梯形一定完全一样。 ( )
辨析:受平行四边形有无数条高的影响,误认为可以画无数条高。
易错辨析
辨析:两个完全一样的梯形能拼成一个平行四边形,但能拼成一个平行四边形的两个梯形不一定完全一样。
(3)两个长方形的周长相等,它们的面积也一定相等。 ( )
辨析:周长相等,只能说明长与宽的和相等,但不能说明长和宽分别相等,所以面积不一定相等。
4.下图是一张长方形纸折起来后的图形,已知∠1=50°,求∠2的度数。
∠2=180°-50°×2=80°
提分点 1
计算角的度数
5.在长是6.4 cm,宽是5.6 cm的长方形纸中,最多可以剪出多少个半径是1 cm的圆?
半径是1 cm,直径是2 cm。长方形长里有6.4÷2≈3(个)直径,宽里有5.6÷2≈2(个)直径,所以最多可以剪出3×2=6(个)半径是1 cm的圆。
提分点 2
动手操作
54
6.如图,∠1=∠2=∠3,图中所有锐角的和是180°,∠1+∠2+∠3=( )°。
(1)0.05 m2=( ) dm2
6 m2 8 dm2=( ) m2
(2)一个三角形的面积是12.9 dm2,底是6 dm,高是( ) dm。
1.填一填。
考点
平面图形的周长和面积
5
6.08
4.3
(3)一个圆的直径是6 cm,这个圆的周长是( ) cm,面积是( )cm2。
(4)一个直角梯形的上底是4 cm,下底和高都是10 cm,这个梯形的面积是( )cm2。
(5)一个圆环,内圆直径是6 cm,环宽1 cm,这个圆环的面积是( )cm2。
18.84
28.26
70
21.98
2.计算下面图形的周长和面积。(单位: cm)
周长:(6+7)×2=26(cm)
面积:5×7=35(cm2)
3.求阴影部分的面积。(单位: cm)
(5+8)×5÷2=32.5(cm2)
辨析:通过割补发现,阴影部分相当于是一个梯形。
4.一块直角梯形麦地,上底长60 m,若将上底延长20 m就得到一个正方形。如果每平方米收小麦0.6 kg,这块地可以收小麦多少千克?
60+20=80(m)
(60+80)×80÷2=5600(m2)
0.6×5600=3360(kg)
答:这块地可以收小麦3360 kg。
5.下面的做法对吗?若不对,请改正。
易错辨析
不对。改正: 3.14×12÷2+12=30.84(cm)
求右面半圆形的周长。
3.14×12÷2=18.84( cm)
辨析:计算半圆形的周长时易漏掉直径。
3.14×42÷4-4×4÷2=4.56(cm2)
6.求阴影部分的面积。(单位: cm)
提分点 1
用“割补法”计算图形的面积
7.下图中梯形的面积是多少?
8×8÷2=32(cm2)
提分点 2
梯形面积的变式练习
8.求下图中阴影部分的面积。(单位: cm)
(4×2+12)×4÷2-4×2×4÷2 =24(cm2)
整理和复习
6
二维图像是指不包含深度信息的平面图像。 二维即左右、上下四个方向,不存在前后。在一张纸上的内容就可以看做成是二维。也就是平时我们所说的平面图形。常应用于人脸识别技术,用摄像机或摄像头采集含有人脸的图像,并自动在图像中检测和跟踪人脸,进而对检测到的人脸进行脸部识别,通常也叫做人像识别、面部识别。
举手回答:我们学过哪些平面图形?你能对学过的图形进行分类吗?
图形都是由线组成,那么我们就从复习线开始复习几何图形。
1. 平面图形的分类
封闭图形
不封闭图形
直线 射线 线段 角
平行线 相交线
四边形
平面图形
长方形
圆
正方形
平行四边形
梯形
三角形
举手回答:三角形可以怎样分类分类?应该怎样分类?
1. 平面图形的分类
三角形按角分
锐角三角形
直角三角形
钝角三角形
(三个角都是锐角)
(有一个角是直角)
(有一个角是钝角)
三角形
等腰三角形
等边三角形
三角形按边分
(两条边相等)
(三条边都相等)
不等边三角形
(三条边都不相等)
举手回答:你能说说四边形之间的关系吗?
1. 平面图形的分类
四边形
平行四边形
长方形
正方形
梯形
等腰梯形
直角梯形
2. 直线、射线和线段
射线
线段
直线
不同点
相同点
名称
能否延长
能
不能
不能
能否测量长度
1个
无
都是直
直的线
端点个数
2个
可以向两
端无限延长
可以向一
端无限延长
不能向两
端无限延长
过点画线
经过一点可以画无数条直线。
从一点可以引出无数条射线。
经过两点只可以画一条直线。
2. 直线、射线和线段
3. 同一平面内两条直线的位置关系
两直线的
位置关系
相交
不相交
垂直
不垂直
平行
4. 角的分类
{8799B23B-EC83-4686-B30A-512413B5E67A}角的
名称
条 件
图例
锐角
小于900的角
直角
等于900的角
钝角
大于900而小于1800的角
平角
等于1800的角
周角
等于3600的角
在放大镜下看角,它的大小会有变化吗?
不论放大多少倍角的度数都不变。
举手回答:各个角的度数分别是多少?
5. 平面图形的特点
{8799B23B-EC83-4686-B30A-512413B5E67A}名称
图例
特点
长方形
正方形
平 行
四边形
三角形
梯 形
圆 形
对边相等,四个角都是直角。
四条边都相等,四个角都是直角。
对边平行且相等,相对的角相等。
由三条线段围成,内角和是180度。
只有一组对边平行的四边形。
在同圆(等圆)中,所有的半径都相等,所有的直径都相等。
6. 圆
圆是平面图形上封闭的曲线图形
一个圆有无数条半径,一般用字母r表示;有无数条直径,一般用字母d表示。
1
同一个圆内,直径的长度是半径的2倍,即:d=2r。
2
3
圆是轴对称图形,它有无数条对称轴。
7.平面图形的周长和面积公式
C=2(ɑ+b)
S=ab
C=4a????
S=ɑ2
S=ɑh
C=2πr =πd
S=πr2
S=ɑh÷2
S=?(ɑ+b)h÷2
a
b
a
a
h
r
a
h
a
b
h
举手回答:我们学过哪些图形的周长与面积?说一说他们的公式分别是什么?
这些计算公式是怎样推导出来的?它们之间有什么联系?
利用割补、转化的方法来推导图形的面积公式。
长方形的面积是研究其它图形面积的基础。
长方形和正方形是用面积单位量出来的。
平行四边形转化成长方形。
两个完全相同的三角形或梯形都可以拼成平行四边形。
8.平面图形的周长和面积公式
9.三角形三边的关系
13cm
4cm
7cm
三角形其中两条线段的和大于第三条线段时,这样的三条线段才能组成一个三角形。
同桌交流:试着用自己的话说一说,三角形第三条边的取值在什么范围?
在括号里填上合适的计量单位。
北京至上海的铁路长约1463( )。
足球场的面积约为7500( )。
东北虎的体重可达320( )。
小虹家的冰箱容积有240 ( )。
km
kg
m2
L
下面说法是否正确?对的画“√”,错的画“×”。
(1)大于90°的角叫钝角。
(2)角的两条边越长,角就越大。
( )
( )
(3)直线的两端可以无限延长。
( )
(4)可以画一条长10厘米的直线。
( )
(5)平角就是一条直线。
( )
√
×
×
×
×
大于90°而小于180°
角的大小与角的两边的长短无关,与角的张口的大小有关。
只要是角,就是由一个顶点和两条边组成。
直线是不可度量。
做两个一样的平行四边形纸片。把它们重合在一起,将上面的平行四边形绕它的一个顶点旋转180度,再通过平移使它与下面的平行四边形重合。观察两个平行四边形的各条边与各个角,你有什么发现?
旋转和平移后的图形,各边与各个角都不变。
(1)请你画一条从蘑菇房到小木屋最近的路。
(2)请你画一条从蘑菇房通向小河最近的路。
动手操作。
计算下面各图形的周长和面积。(单位:m)
C:30+40+50
=120(m)
S:30×40÷2
=1200÷2
=600(m2)
C:6+6+7.5+10.5=30(m)
S:(6+10.5)×6÷2
=16.5 ×6÷2
=49.5( m2 )
C:3+5×2+3.14×5÷2+(5-2)
=15.7(m)
S:3.14×( 5÷2 )2÷2
+5 ×3
=9.8125+15
=24.8125( m2 )
如果一个正方形能够被分割为若干个边长不等的小正方形,则这个正方形成为完美正方形。下面的正方形是已知包含21个小正方形的完美正方形(称为21阶完美正方形),这个迄今为止最小阶数的完美正方形,分割方法如图所示,其中小正方形中心的数字代表其边长。请计算这个完美正方形的边长。(单位:厘米)
50+35+27=112(厘米)
答:这个正方形的周长是112厘米。
(1) 图中有( )条直线,( )条射线,( )条线段。
(2)钟面上3时整,时针和分针组成的角是( )角。
(3)一个三角形的两条边的长分别是8 cm和12 cm,第三条边最长是( ) cm,最短是( ) cm。(填整厘米数)
1.填一填。
考点
平面图形的认识
1
8
6
直
19
5
(4)一个三角形的两个角分别是78°和27°,第三个角是( )°。
(5)( )形和( )形是特殊的平行四边形,它们的对边分别( )且( )。
(6)如图,圆的半径是( )cm,长方形的周长是( ) cm,它有( )条对称轴。
75
长方
正方
平行
相等
3
30
一
2.选择。(将正确答案的字母填在括号里)
(1)把平行四边形任意分割成两个梯形,这两个梯形的
( )相等。
A.高 B.周长 C.上下底之和 D.面积
(2)下面图形中,不是轴对称图形的是( )。
A.半圆形 B.长方形
C.平行四边形 D.等腰梯形
A
C
(3)在同一平面内,与已知直线相距5 cm的直线有( )条。
A.1 B.2 C.无数 D.0
(4)一个三角形三个角的度数都不相等,其中最小的角是45°,这个三角形一定是( )三角形。
A.锐角 B.直角
C.钝角 D.等腰直角
B
A
3.判断。(对的画“√”,错的画“×”)
(1)从平行四边形的一个顶点出发最多可以画两条高。 ( )
(2)如果两个梯形能拼成一个平行四边形,那么这两个梯形一定完全一样。 ( )
辨析:受平行四边形有无数条高的影响,误认为可以画无数条高。
易错辨析
辨析:两个完全一样的梯形能拼成一个平行四边形,但能拼成一个平行四边形的两个梯形不一定完全一样。
(3)两个长方形的周长相等,它们的面积也一定相等。 ( )
辨析:周长相等,只能说明长与宽的和相等,但不能说明长和宽分别相等,所以面积不一定相等。
4.下图是一张长方形纸折起来后的图形,已知∠1=50°,求∠2的度数。
∠2=180°-50°×2=80°
提分点 1
计算角的度数
5.在长是6.4 cm,宽是5.6 cm的长方形纸中,最多可以剪出多少个半径是1 cm的圆?
半径是1 cm,直径是2 cm。长方形长里有6.4÷2≈3(个)直径,宽里有5.6÷2≈2(个)直径,所以最多可以剪出3×2=6(个)半径是1 cm的圆。
提分点 2
动手操作
54
6.如图,∠1=∠2=∠3,图中所有锐角的和是180°,∠1+∠2+∠3=( )°。
(1)0.05 m2=( ) dm2
6 m2 8 dm2=( ) m2
(2)一个三角形的面积是12.9 dm2,底是6 dm,高是( ) dm。
1.填一填。
考点
平面图形的周长和面积
5
6.08
4.3
(3)一个圆的直径是6 cm,这个圆的周长是( ) cm,面积是( )cm2。
(4)一个直角梯形的上底是4 cm,下底和高都是10 cm,这个梯形的面积是( )cm2。
(5)一个圆环,内圆直径是6 cm,环宽1 cm,这个圆环的面积是( )cm2。
18.84
28.26
70
21.98
2.计算下面图形的周长和面积。(单位: cm)
周长:(6+7)×2=26(cm)
面积:5×7=35(cm2)
3.求阴影部分的面积。(单位: cm)
(5+8)×5÷2=32.5(cm2)
辨析:通过割补发现,阴影部分相当于是一个梯形。
4.一块直角梯形麦地,上底长60 m,若将上底延长20 m就得到一个正方形。如果每平方米收小麦0.6 kg,这块地可以收小麦多少千克?
60+20=80(m)
(60+80)×80÷2=5600(m2)
0.6×5600=3360(kg)
答:这块地可以收小麦3360 kg。
5.下面的做法对吗?若不对,请改正。
易错辨析
不对。改正: 3.14×12÷2+12=30.84(cm)
求右面半圆形的周长。
3.14×12÷2=18.84( cm)
辨析:计算半圆形的周长时易漏掉直径。
3.14×42÷4-4×4÷2=4.56(cm2)
6.求阴影部分的面积。(单位: cm)
提分点 1
用“割补法”计算图形的面积
7.下图中梯形的面积是多少?
8×8÷2=32(cm2)
提分点 2
梯形面积的变式练习
8.求下图中阴影部分的面积。(单位: cm)
(4×2+12)×4÷2-4×2×4÷2 =24(cm2)
