第三章《不等式》水平测试(3)
文档属性
| 名称 | 第三章《不等式》水平测试(3) |

|
|
| 格式 | zip | ||
| 文件大小 | 167.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-13 00:00:00 | ||
图片预览

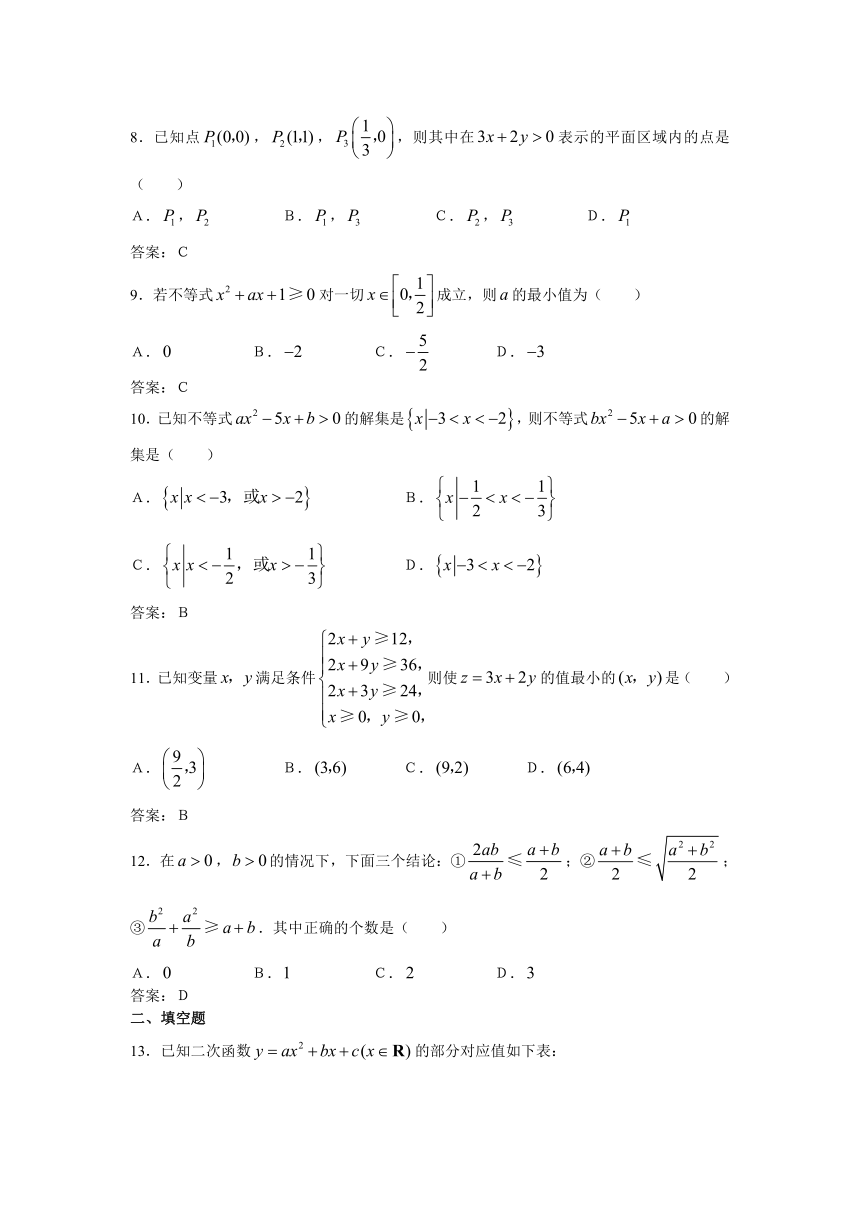

文档简介
第三章《不等式》水平测试(3)
一、选择题
1.若实数满足,且,那么下列选项中不一定成立的是( )
A. B. C. D.
答案:C
2.下列不等式中解集为实数集的是( )
A. B.
C. D.
答案:D
3.不等式的解集为( )
A. B.
C. D.
答案:A
4.不等式对一切恒成立,则实数的取值范围是( )
A. B. C. D.
答案:C
5.如果方程的两个实根一个小于,另一个大于,那么实数的取值范围是( )
A. B. C. D.
答案:D
6.若,,,,则( )
A. B. C. D.
答案:B
7.已知,,的等差中项是,且,,则的最小值是( )
A. B. C. D.
答案:C
8.已知点,,,则其中在表示的平面区域内的点是( )
A., B., C., D.
答案:C
9.若不等式对一切成立,则的最小值为( )
A. B. C. D.
答案:C
10.已知不等式的解集是,则不等式的解集是( )
A. B.
C. D.
答案:B
11.已知变量满足条件则使的值最小的是( )
A. B. C. D.
答案:B
12.在,的情况下,下面三个结论:①;②;③.其中正确的个数是( )
A. B. C. D.
答案:D
二、填空题
13.已知二次函数的部分对应值如下表:
则不等式的解集是 .
答案:
14.给出平面区域如右图阴影部分所示,目标函数,若当且仅当,时,目标函数取最小值,则实数的取值范围是 .
答案:
15.已知对任意正实数恒成立,则正实数最小值为 .
答案:4
16.若均为实数,则使不等式和都成立的一组值是 (只要写出适合条件的一组值即可).
答案:如等
三、解答题
17.设,试比较与的大小.
解:,
.
18.解不等式.
解:原不等式可变形为,
即
解得.
故原不等式的解集为.
19.设,已知关于的一元二次方程有两实数,,且,求实数的取值范围.
解:设.
是方程的两实根,且,,
即
解得,或.
实数的取值范围是.
20.已知满足约束条件求的最大值.
解:画出约束条件所示的区域,如下图图阴影部发所示.
作直线与平行,
当经过点时,原点到的距离最大.
由解得故.
因此,当,时,取最大值,此时,.
21.已知函数.
(1)若,解关于的不等式;
(2)若对于,恒成立,求实数的取值范围.
解:(1)由已知得,即,解得,或.
所以不等式的解集为;
(2),令,则是关于的一次函数,且一次项的系数为.
,
当时,,不合题意;
当时,为上的增函数.
恒成立,
只要使的最大值即可.
即,
解得.
综上所知,的取值范围是.
22.某商场预计全年分批购入每台价值为元的电视机共台,每批都购入台,且每批均需付运费元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运算)成正比,若每批购入台,则全年需要付运费和保管费元,现在全年只有元资金可以用于支付这笔费用,请问能否恰当安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
解:设每批购入电视机台时,今年费用为元,保管与款子批购入电视机的总价值的比例系九为,但题意有,
则当时,,
代入上述,解得,
故,即时,等号成立.
所以每批购进电视机台时,全年的奖金元才够用.
一、选择题
1.若实数满足,且,那么下列选项中不一定成立的是( )
A. B. C. D.
答案:C
2.下列不等式中解集为实数集的是( )
A. B.
C. D.
答案:D
3.不等式的解集为( )
A. B.
C. D.
答案:A
4.不等式对一切恒成立,则实数的取值范围是( )
A. B. C. D.
答案:C
5.如果方程的两个实根一个小于,另一个大于,那么实数的取值范围是( )
A. B. C. D.
答案:D
6.若,,,,则( )
A. B. C. D.
答案:B
7.已知,,的等差中项是,且,,则的最小值是( )
A. B. C. D.
答案:C
8.已知点,,,则其中在表示的平面区域内的点是( )
A., B., C., D.
答案:C
9.若不等式对一切成立,则的最小值为( )
A. B. C. D.
答案:C
10.已知不等式的解集是,则不等式的解集是( )
A. B.
C. D.
答案:B
11.已知变量满足条件则使的值最小的是( )
A. B. C. D.
答案:B
12.在,的情况下,下面三个结论:①;②;③.其中正确的个数是( )
A. B. C. D.
答案:D
二、填空题
13.已知二次函数的部分对应值如下表:
则不等式的解集是 .
答案:
14.给出平面区域如右图阴影部分所示,目标函数,若当且仅当,时,目标函数取最小值,则实数的取值范围是 .
答案:
15.已知对任意正实数恒成立,则正实数最小值为 .
答案:4
16.若均为实数,则使不等式和都成立的一组值是 (只要写出适合条件的一组值即可).
答案:如等
三、解答题
17.设,试比较与的大小.
解:,
.
18.解不等式.
解:原不等式可变形为,
即
解得.
故原不等式的解集为.
19.设,已知关于的一元二次方程有两实数,,且,求实数的取值范围.
解:设.
是方程的两实根,且,,
即
解得,或.
实数的取值范围是.
20.已知满足约束条件求的最大值.
解:画出约束条件所示的区域,如下图图阴影部发所示.
作直线与平行,
当经过点时,原点到的距离最大.
由解得故.
因此,当,时,取最大值,此时,.
21.已知函数.
(1)若,解关于的不等式;
(2)若对于,恒成立,求实数的取值范围.
解:(1)由已知得,即,解得,或.
所以不等式的解集为;
(2),令,则是关于的一次函数,且一次项的系数为.
,
当时,,不合题意;
当时,为上的增函数.
恒成立,
只要使的最大值即可.
即,
解得.
综上所知,的取值范围是.
22.某商场预计全年分批购入每台价值为元的电视机共台,每批都购入台,且每批均需付运费元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运算)成正比,若每批购入台,则全年需要付运费和保管费元,现在全年只有元资金可以用于支付这笔费用,请问能否恰当安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
解:设每批购入电视机台时,今年费用为元,保管与款子批购入电视机的总价值的比例系九为,但题意有,
则当时,,
代入上述,解得,
故,即时,等号成立.
所以每批购进电视机台时,全年的奖金元才够用.
