江苏省南京市第十四中学2020-2021学年高一下学期3月检测数学试题 Word版含解析
文档属性
| 名称 | 江苏省南京市第十四中学2020-2021学年高一下学期3月检测数学试题 Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 13:53:01 | ||
图片预览



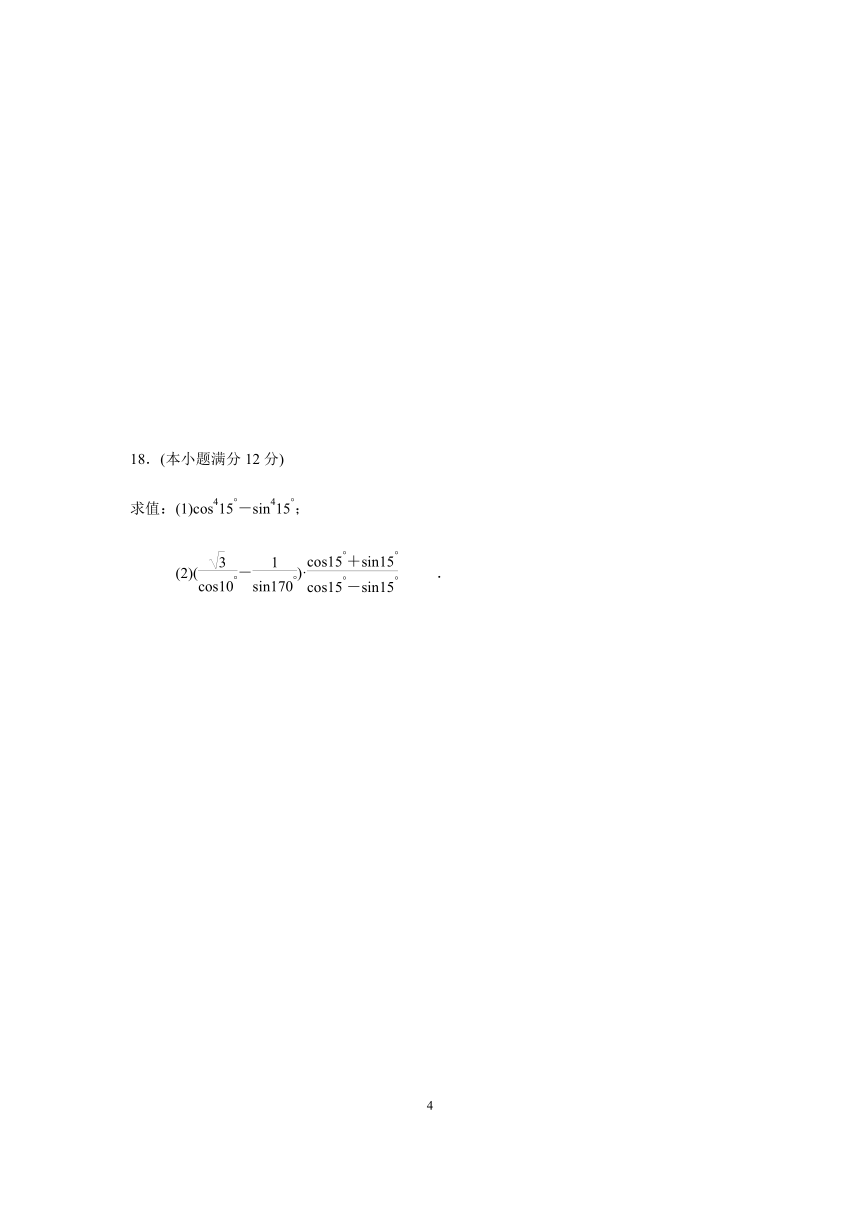

文档简介
南京市十四中2020-2021学年第二学期高一数学3月学情检测 满分:150分 时间:120分钟
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案直接填在答题卡相应位置上.
1.若=(1,-2),=(1,-1),则等于( )
A.(-2,3) B.(0,1) C.(-1,2) D.(2,-3)
2.若tanα=3,则的值为( )
A.2 B.3 C.4 D.6
3.若cos24°cos36°-cos66°cos54°=( )
A.0 B. C. D.-
4.已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是( )
4933950217170A
A
A.a+2b B.2a+b C.a-2b D.2a-b
5797550297180C
C
5067300990605067300990604400550990605.如图,在△ABC中,AD⊥AB,=,||=1,则=
539750077470D
D
4267200297180B
B
43999150A.2 B. C. D.
6.已知平面上A,B,C三点不共线,O是不同于A,B,C的任意一点,且(-)(+则△ABC是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
7.已知|a|=1,|b|=,且a⊥(a+b),则向量a在b方向上的投影向量为( )
A.b B.b C.b D.-b
8.若sin且β∈[π,]则α+β的值是( )
A. B. C.或 D.或
二、不定项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列等式成立的是( )
A.cos215°-sin215°= B.sin40°+cos40°=sin70°
C.sincos= D.tan15°=2-
10.对于菱形ABCD,给出下列各式,其中正确的有( )
A.= B.||=||
C.|-|=|+| D.||2+||2=4||2
11.已知向量a=(1,-2),b=(-1,m),则( )
A.若a与b垂直,则m=-1 B.若a∥b,则ab的值为-5
C.若m=1,则|a-b|= D.若m=-2,则a与b的夹角为60°
12.已知函数f(x)=sin2x+2sinxcosx-cos2x,x∈R,则( )
A.-2≤f(x)≤2 B.f(x)在区间是(0,π)上只有1个零点
C.f(x)的最小正周期为π D.x=为f(x)图象的一条对称轴
三、填空题:本题共4小题,每小题5分,共20分。第16题两空,第一空2分,第二空3分.
13.在△ABC中,已知tanA,tanB是方程3x2-7x+2=0的两根,求tanC= .
14.若e1,e2是夹角为60°的两个单位向量,向量a=2e1+e2,则|a|= .
4616450397510C
C
3863975393700D
D
4203700693420E
E
4003675494030367030049530046005754940303667125494030400050049530015.如图,在等腰梯形ABCD中,DC=AB,BC=CD=DA,DE⊥AC于点E,如果选择向量与作基底,则可用该基底表示为 .
4933950298450B
B
3533775297180A
A
367030099060
16.公元前6世纪,古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图,发现了黄金分割值约为0.618,这一数值也可以表示为m=2sin18°.若m2+n2=4,则= .(用数字作答)
四、解答题:本大题共6小题,共70分,请在答题卡指定区域内作答,'解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题满分10分)
已知
(1)求实数n的值;
(2)若⊥,求实数m的值.
18.(本小题满分12分)
求值:(1);
(2) .
19.(本小题满分12分)
已知cos(α-)=-,sin(-β)=,且α∈(,π),β∈(0,).求:
(1);
(2)tan(α+β).
20.(本小题满分12分)
3533775594360D
D
4968875594360C
C
3222625693420如图,在平行四边形ABCD中,点E,F,G分别在边AB,AD,BC上,且满足AE=AB,AF=AD,BG=BC,设=a,=b.
3536950990603333750396240480060045720G
G
3181350278130F
F
(1)用a,b表示,;
3467100184150E
E
4467225118110B
B
306705099060A
A
(2)若EF⊥EG,=2ab,求角A的值.
21.(本小题满分12分)
已知向量a=(sinx,),b=(cosx,-1).
(1)当a∥b时,求tan2x的值;
(2)设函数f(x)=2(a+b)b,且x∈(0,),求f(x)的最大值以及对应的x的值.
22.(本小题满分12分)
在平面直角坐标系中,O为坐标原点,已知向量a=(-1,2),点A(8,0),B(n,t),C(ksinθ,t),(0≤θ≤).
(1)若⊥a,且||=||,求向量;
(2)若向量与向量a共线,当k>4,且tsinθ取得最大值4时,求.
南京市十四中2020-2021学年第二学期高一数学3月学情检测 解析版 满分:150分 时间:120分钟
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案直接填在答题卡相应位置上.
1.若=(1,-2),=(1,-1),则等于( )
A.(-2,3) B.(0,1) C.(-1,2) D.(2,-3)
【答案】B
【考点】平面向量的坐标运算
【解析】由题意=-= (1,-1)-(1,-2)]=(0,1),故答案选B.
2.若tanα=3,则的值为( )
A.2 B.3 C.4 D.6
【答案】D
【考点】二倍角公式、齐次式化简
【解析】由题意==2tanα=6,故答案选D.
3.若cos24°cos36°-cos66°cos54°=( )
A.0 B. C. D.-
【答案】B
【考点】诱导公式、两角和的余弦公式
【解析】由题意可知cos66°=sin24°,cos54°=sin36°,所以原式=cos24°cos36°-cos66°cos54°=cos24°cos36°-sin24°sin36°=cos(24°+36°)=cos60°=,故答案选B.
4.已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是( )
A.a+2b B.2a+b C.a-2b D.2a-b
【答案】D
【考点】平面向量的数量积、垂直关系应用
【解析】由题意|a|=|b|=1,ab=|a||b|cos60°=,所以(a+2b)b=ab+2|b|2=+2=≠0,故选项A错误;(2a+b)b=2ab+|b|2=1+1=2≠0,故选项B错误;(a-2b)b=ab-2|b|2=-2=-≠0,故选项C错误;(2a-b)b=2ab-|b|2=1-1=0,即2a-b与b垂直,故选项D正确;综上答案选D.
5467350398780D
D
506730010287049307752540A
A
5797550297180C
C
5067300990604400550990605.如图,在△ABC中,AD⊥AB,=,||=1,则=
4267200297180B
B
43999150A.2 B. C. D.
【答案】D
【考点】平面向量中数量积的应用
【解析】由题意因为AD⊥AB,所以=0,所以=(+)=0+=||||cos∠ADB=||2=,故答案选D.
6.已知平面上A,B,C三点不共线,O是不同于A,B,C的任意一点,且(-)(+则△ABC是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
【答案】A
【考点】利用平面向量的运算判断三角形的形状
【解析】取BC边上的中点D,则有+=2,则(-)(+)=2=0,可得BC⊥AD,又因为点D为BC边上的中点,所以△ABC是等腰三角形,故答案选A.
7.已知|a|=1,|b|=,且a⊥(a+b),则向量a在b方向上的投影向量为( )
A.b B.b C.b D.-b
【答案】A
【考点】利用平面向量的垂直关系、数量积求解投影向量
【解析】由题意|a|=1,|b|=,且a⊥(a+b),所以a(a+b)=|a|2+ab=|a|2+|a||b|cos< a,b >=1+1 cos=0,解得=,则向量a在b方向上的投影向量为bcos=b,(或用公式:=b)故答案选A.
8.若sin且β∈[π,]则α+β的值是( )
A. B. C.或 D.或
【答案】B
【考点】给值求角问题的应用
【解析】因为β∈[π,],所以2又sin2α=>0,所以2则cos2α=-=-,又因为β-α∈所以-=-,所以cos(α+β)=cos[2α+(β-α)]=cos2α-sin2α=-×(-)-×=,又因为β∈[π,],所以α+β∈[,2π],所以α+β=,故答案选B.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列等式成立的是( )
A.cos215°-sin215°= B.sin40°+cos40°=sin70°
C.sincos= D.tan15°=2-
【答案】ACD
【考点】三角恒等变换的公式灵活应用
【解析】由题意,对于选项A,cos215°-sin215°=cos30°=,故选项A正确;对于选项B,sin40°+cos40°=cos60°sin40°+sin60°cos40°=sin(40°-60°)=-sin20°,故选项B错误;对于选项C,sincos=sin=,所以选项C正确;对应选项D,tan15°=tan(60°-45°)===2-,故选项D正确;综上,答案选项ACD.
10.对于菱形ABCD,给出下列各式,其中正确的有( )
A.= B.||=||
C.|-|=|+| D.||2+||2=4||2
【答案】BCD
【考点】平面向量的模、平行或垂直问题、数量积等应用
【解析】由题意,对于选项A,由于与方向不同,故≠,故选项A错误;对于选项B,因为四边形ABCD为菱形,所以||=||,故选项B正确;对于选项C,|-|=|+|=2||,而|+|=2||,且||=||,所以|-|=|+|,故选项C正确;对于选项D,||2+||2=|+|2+|-|2=2||2+2||2=4||2,故选项D正确;综上,答案选BCD.
11.已知向量a=(1,-2),b=(-1,m),则( )
A.若a与b垂直,则m=-1 B.若a∥b,则ab的值为-5
C.若m=1,则|a-b|= D.若m=-2,则a与b的夹角为60°
【答案】BC
【考点】平面向量的平行与垂直问题、数量积的坐标运算及求模
【解析】由题意,对于选项A,若a与b垂直,则1×(-1)+m×(-2)=0,解得x=-,故选项A错误;对于选项B,若a∥b,则m-(-2)×(-1)=0,解得m=2,则b=(-1,2),所以ab=(1,-2) (-1,2)=1×(-1)+2×(-2)=-5,故选项B正确;对于选项C,若m=1,则b=(-1,1),所以a-b=(1,-2)-(-1,1)=(2,-3),所以|a-b|=,故选项C正确;对于选项D,若m=-2,则b=(-1,-2),所以ab=(1,-2) (-1,-2)=3,且|a|=,|b|=,所以cos==,故选项D错误;综上答案选BC.
12.已知函数f(x)=sin2x+2sinxcosx-cos2x,x∈R,则( )
A.-2≤f(x)≤2 B.f(x)在区间是(0,π)上只有1个零点
C.f(x)的最小正周期为π D.x=为f(x)图象的一条对称轴
【答案】ACD
【考点】利用三角函数公式化简解决三角函数的图象与性质
【解析】由题意函数f(x)可化简为f(x)=sin2x-cos2x=2sin(2x-),则最小正周期为T==π,值域为[-2,2],故选项A、C正确;因为f()=2sin(2×-)=2,所以x=为f(x)图象的一条对称轴,故选项D正确;令f(x)=0,则2x-=kπ (k∈Z),解得x=+(k∈Z),则在区间(0,π)上可取k=0,1,即x=,x=,故选项B错误;综上,答案选ACD.
三、填空题:本题共4小题,每小题5分,共20分。第16题两空,第一空2分,第二空3分.
13.在△ABC中,已知tanA,tanB是方程3x2-7x+2=0的两根,求tanC= .
【答案】-7
【考点】两角和的正切公式、诱导公式在三角形中的应用
【解析】由题意可得tanA+tanB=,tanAtanB=,所以tanC=tan[π-(A+B)]=-tan(A+B)=-=-=-7,故答案为-7.
14.若e1,e2是夹角为60°的两个单位向量,向量a=2e1+e2,则|a|= .
【答案】
【考点】平面向量中数量积与模的求解
【解析】由题意|a|====,故答案为.
4616450397510C
C
3863975393700D
D
4203700693420E
E
4003675494030367030049530046005754940303667125494030400050049530015.如图,在等腰梯形ABCD中,DC=AB,BC=CD=DA,DE⊥AC于点E,如果选择向量与作基底,则可用该基底表示为 .
4933950298450B
B
3533775297180A
A
367030099060
【答案】+
【考点】平面向量的基本定理的应用
【解析】由题意可得E为AC的中点,所以=+=+=+,故答案为+.
16.公元前6世纪,古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图,发现了黄金分割值约为0.618,这一数值也可以表示为m=2sin18°.若m2+n2=4,则= .(用数字作答)
【答案】-
【考点】文化题:三角函数公式化简、三角恒等变换化简求值
【解析】由题意====-,故答案为-.
四、解答题:本题共6小题,共70分。需要写出解答过程,请把答案直接填在答题卡相应位置上.
17.(本小题满分10分)
已知
(1)求实数n的值;
(2)若⊥,求实数m的值.
【考点】平面向量的平行与垂直的条件应用
【解析】
因为m),
所以n),
(1)因为所以可得3×(3+m+n)-m×3=0,解得n=-3;
(2)因为,=+=(4,m-3),
因为⊥,所以所以解得m=±1.
18.(本小题满分12分)
求值:(1);
(2)
【考点】三角恒等变换应用
【解析】
(1)原式=(cos215°+sin215°) (cos215°-sin215°)=cos215°-sin215°=cos30°=;
(2) 原式
19.(本小题满分12分)
已知cos(α-)=-,sin(-β)=,且α∈(,π),β∈(0,).求:
(1);
(2)tan(α+β).
【考点】二倍角公式的应用、给值求值问题:变角(构造角)
【解析】
(1)
∴<α-<π,-<-β<,
∴sin(α-)==
cos(-β)==
]si
=;
(2)
,
∴
20.(本小题满分12分)
3533775594360D
D
4968875594360C
C
3222625693420如图,在平行四边形ABCD中,点E,F,G分别在边AB,AD,BC上,且满足AE=AB,AF=AD,BG=BC,设=a,=b.
3536950990603333750396240480060045720G
G
3181350278130F
F
(1)用a,b表示,;
3467100184150E
E
4467225118110B
B
306705099060A
A
(2)若EF⊥EG,=2ab,求角A的值.
【考点】平面向量的数量积应用
【解析】
(1)由平面向量的线性运算可知=-=-=b-a,
=+=+=b+a,
(2)由题意,因为EF⊥EG,所以=(b-a)(b+a)=(b-a)(b+a)=(|b|2-|a|2)=0,解得|a|=|b|,
所以=a(b+a)=ab+|a|2=2ab,
化简得2ab=|a|2,即2|a||b|cosA=|a||a|=|a||b|,
所以cosA=,
又因A∈(0,π),所以A=.
21.(本小题满分12分)
已知向量a=(sinx,),b=(cosx,-1).
(1)当a∥b时,求tan2x的值;
(2)设函数f(x)=2(a+b)b,且x∈(0,),求f(x)的最大值以及对应的x的值.
【考点】平面向量中平行的坐标运算、正切的二倍角公式运用、三角恒等变换与三角函数的图象与性质综合运用
【解析】
(1)因为a//b,所以.
因此tan2x===-.
(2)由题意f(x)=2(a+b)b=2
因此f(x)的最大值为
由x∈(0,),得此时.
22.(本小题满分12分)
在平面直角坐标系中,O为坐标原点,已知向量a=(-1,2),点A(8,0),B(n,t),C(ksinθ,t),(0≤θ≤).
(1)若⊥a,且||=||,求向量;
(2)若向量与向量a共线,当k>4,且tsinθ取得最大值4时,求.
【考点】三角函数与平面向量综合应用、三角函数的图象与性质及变换应用
【解析】
(1)由题设知
因为所以8-n+2t=0,
又所以,解得t=±8;
当t=8时,n=24;当t=-8时,n=-8.
所以,或.
(2)由题设知
因为与a共线,所以t=-2ksinθ+16,
tsinθ=(-2ksinθ+16)
因为k>4,所以
所以当时,tsinθ取得最大值
由得k=8,此时
所以=(8,0)(4,8)=32.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案直接填在答题卡相应位置上.
1.若=(1,-2),=(1,-1),则等于( )
A.(-2,3) B.(0,1) C.(-1,2) D.(2,-3)
2.若tanα=3,则的值为( )
A.2 B.3 C.4 D.6
3.若cos24°cos36°-cos66°cos54°=( )
A.0 B. C. D.-
4.已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是( )
4933950217170A
A
A.a+2b B.2a+b C.a-2b D.2a-b
5797550297180C
C
5067300990605067300990604400550990605.如图,在△ABC中,AD⊥AB,=,||=1,则=
539750077470D
D
4267200297180B
B
43999150A.2 B. C. D.
6.已知平面上A,B,C三点不共线,O是不同于A,B,C的任意一点,且(-)(+则△ABC是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
7.已知|a|=1,|b|=,且a⊥(a+b),则向量a在b方向上的投影向量为( )
A.b B.b C.b D.-b
8.若sin且β∈[π,]则α+β的值是( )
A. B. C.或 D.或
二、不定项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列等式成立的是( )
A.cos215°-sin215°= B.sin40°+cos40°=sin70°
C.sincos= D.tan15°=2-
10.对于菱形ABCD,给出下列各式,其中正确的有( )
A.= B.||=||
C.|-|=|+| D.||2+||2=4||2
11.已知向量a=(1,-2),b=(-1,m),则( )
A.若a与b垂直,则m=-1 B.若a∥b,则ab的值为-5
C.若m=1,则|a-b|= D.若m=-2,则a与b的夹角为60°
12.已知函数f(x)=sin2x+2sinxcosx-cos2x,x∈R,则( )
A.-2≤f(x)≤2 B.f(x)在区间是(0,π)上只有1个零点
C.f(x)的最小正周期为π D.x=为f(x)图象的一条对称轴
三、填空题:本题共4小题,每小题5分,共20分。第16题两空,第一空2分,第二空3分.
13.在△ABC中,已知tanA,tanB是方程3x2-7x+2=0的两根,求tanC= .
14.若e1,e2是夹角为60°的两个单位向量,向量a=2e1+e2,则|a|= .
4616450397510C
C
3863975393700D
D
4203700693420E
E
4003675494030367030049530046005754940303667125494030400050049530015.如图,在等腰梯形ABCD中,DC=AB,BC=CD=DA,DE⊥AC于点E,如果选择向量与作基底,则可用该基底表示为 .
4933950298450B
B
3533775297180A
A
367030099060
16.公元前6世纪,古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图,发现了黄金分割值约为0.618,这一数值也可以表示为m=2sin18°.若m2+n2=4,则= .(用数字作答)
四、解答题:本大题共6小题,共70分,请在答题卡指定区域内作答,'解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题满分10分)
已知
(1)求实数n的值;
(2)若⊥,求实数m的值.
18.(本小题满分12分)
求值:(1);
(2) .
19.(本小题满分12分)
已知cos(α-)=-,sin(-β)=,且α∈(,π),β∈(0,).求:
(1);
(2)tan(α+β).
20.(本小题满分12分)
3533775594360D
D
4968875594360C
C
3222625693420如图,在平行四边形ABCD中,点E,F,G分别在边AB,AD,BC上,且满足AE=AB,AF=AD,BG=BC,设=a,=b.
3536950990603333750396240480060045720G
G
3181350278130F
F
(1)用a,b表示,;
3467100184150E
E
4467225118110B
B
306705099060A
A
(2)若EF⊥EG,=2ab,求角A的值.
21.(本小题满分12分)
已知向量a=(sinx,),b=(cosx,-1).
(1)当a∥b时,求tan2x的值;
(2)设函数f(x)=2(a+b)b,且x∈(0,),求f(x)的最大值以及对应的x的值.
22.(本小题满分12分)
在平面直角坐标系中,O为坐标原点,已知向量a=(-1,2),点A(8,0),B(n,t),C(ksinθ,t),(0≤θ≤).
(1)若⊥a,且||=||,求向量;
(2)若向量与向量a共线,当k>4,且tsinθ取得最大值4时,求.
南京市十四中2020-2021学年第二学期高一数学3月学情检测 解析版 满分:150分 时间:120分钟
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案直接填在答题卡相应位置上.
1.若=(1,-2),=(1,-1),则等于( )
A.(-2,3) B.(0,1) C.(-1,2) D.(2,-3)
【答案】B
【考点】平面向量的坐标运算
【解析】由题意=-= (1,-1)-(1,-2)]=(0,1),故答案选B.
2.若tanα=3,则的值为( )
A.2 B.3 C.4 D.6
【答案】D
【考点】二倍角公式、齐次式化简
【解析】由题意==2tanα=6,故答案选D.
3.若cos24°cos36°-cos66°cos54°=( )
A.0 B. C. D.-
【答案】B
【考点】诱导公式、两角和的余弦公式
【解析】由题意可知cos66°=sin24°,cos54°=sin36°,所以原式=cos24°cos36°-cos66°cos54°=cos24°cos36°-sin24°sin36°=cos(24°+36°)=cos60°=,故答案选B.
4.已知单位向量a,b的夹角为60°,则在下列向量中,与b垂直的是( )
A.a+2b B.2a+b C.a-2b D.2a-b
【答案】D
【考点】平面向量的数量积、垂直关系应用
【解析】由题意|a|=|b|=1,ab=|a||b|cos60°=,所以(a+2b)b=ab+2|b|2=+2=≠0,故选项A错误;(2a+b)b=2ab+|b|2=1+1=2≠0,故选项B错误;(a-2b)b=ab-2|b|2=-2=-≠0,故选项C错误;(2a-b)b=2ab-|b|2=1-1=0,即2a-b与b垂直,故选项D正确;综上答案选D.
5467350398780D
D
506730010287049307752540A
A
5797550297180C
C
5067300990604400550990605.如图,在△ABC中,AD⊥AB,=,||=1,则=
4267200297180B
B
43999150A.2 B. C. D.
【答案】D
【考点】平面向量中数量积的应用
【解析】由题意因为AD⊥AB,所以=0,所以=(+)=0+=||||cos∠ADB=||2=,故答案选D.
6.已知平面上A,B,C三点不共线,O是不同于A,B,C的任意一点,且(-)(+则△ABC是( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等边三角形
【答案】A
【考点】利用平面向量的运算判断三角形的形状
【解析】取BC边上的中点D,则有+=2,则(-)(+)=2=0,可得BC⊥AD,又因为点D为BC边上的中点,所以△ABC是等腰三角形,故答案选A.
7.已知|a|=1,|b|=,且a⊥(a+b),则向量a在b方向上的投影向量为( )
A.b B.b C.b D.-b
【答案】A
【考点】利用平面向量的垂直关系、数量积求解投影向量
【解析】由题意|a|=1,|b|=,且a⊥(a+b),所以a(a+b)=|a|2+ab=|a|2+|a||b|cos< a,b >=1+1 cos
8.若sin且β∈[π,]则α+β的值是( )
A. B. C.或 D.或
【答案】B
【考点】给值求角问题的应用
【解析】因为β∈[π,],所以2又sin2α=>0,所以2则cos2α=-=-,又因为β-α∈所以-=-,所以cos(α+β)=cos[2α+(β-α)]=cos2α-sin2α=-×(-)-×=,又因为β∈[π,],所以α+β∈[,2π],所以α+β=,故答案选B.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列等式成立的是( )
A.cos215°-sin215°= B.sin40°+cos40°=sin70°
C.sincos= D.tan15°=2-
【答案】ACD
【考点】三角恒等变换的公式灵活应用
【解析】由题意,对于选项A,cos215°-sin215°=cos30°=,故选项A正确;对于选项B,sin40°+cos40°=cos60°sin40°+sin60°cos40°=sin(40°-60°)=-sin20°,故选项B错误;对于选项C,sincos=sin=,所以选项C正确;对应选项D,tan15°=tan(60°-45°)===2-,故选项D正确;综上,答案选项ACD.
10.对于菱形ABCD,给出下列各式,其中正确的有( )
A.= B.||=||
C.|-|=|+| D.||2+||2=4||2
【答案】BCD
【考点】平面向量的模、平行或垂直问题、数量积等应用
【解析】由题意,对于选项A,由于与方向不同,故≠,故选项A错误;对于选项B,因为四边形ABCD为菱形,所以||=||,故选项B正确;对于选项C,|-|=|+|=2||,而|+|=2||,且||=||,所以|-|=|+|,故选项C正确;对于选项D,||2+||2=|+|2+|-|2=2||2+2||2=4||2,故选项D正确;综上,答案选BCD.
11.已知向量a=(1,-2),b=(-1,m),则( )
A.若a与b垂直,则m=-1 B.若a∥b,则ab的值为-5
C.若m=1,则|a-b|= D.若m=-2,则a与b的夹角为60°
【答案】BC
【考点】平面向量的平行与垂直问题、数量积的坐标运算及求模
【解析】由题意,对于选项A,若a与b垂直,则1×(-1)+m×(-2)=0,解得x=-,故选项A错误;对于选项B,若a∥b,则m-(-2)×(-1)=0,解得m=2,则b=(-1,2),所以ab=(1,-2) (-1,2)=1×(-1)+2×(-2)=-5,故选项B正确;对于选项C,若m=1,则b=(-1,1),所以a-b=(1,-2)-(-1,1)=(2,-3),所以|a-b|=,故选项C正确;对于选项D,若m=-2,则b=(-1,-2),所以ab=(1,-2) (-1,-2)=3,且|a|=,|b|=,所以cos
12.已知函数f(x)=sin2x+2sinxcosx-cos2x,x∈R,则( )
A.-2≤f(x)≤2 B.f(x)在区间是(0,π)上只有1个零点
C.f(x)的最小正周期为π D.x=为f(x)图象的一条对称轴
【答案】ACD
【考点】利用三角函数公式化简解决三角函数的图象与性质
【解析】由题意函数f(x)可化简为f(x)=sin2x-cos2x=2sin(2x-),则最小正周期为T==π,值域为[-2,2],故选项A、C正确;因为f()=2sin(2×-)=2,所以x=为f(x)图象的一条对称轴,故选项D正确;令f(x)=0,则2x-=kπ (k∈Z),解得x=+(k∈Z),则在区间(0,π)上可取k=0,1,即x=,x=,故选项B错误;综上,答案选ACD.
三、填空题:本题共4小题,每小题5分,共20分。第16题两空,第一空2分,第二空3分.
13.在△ABC中,已知tanA,tanB是方程3x2-7x+2=0的两根,求tanC= .
【答案】-7
【考点】两角和的正切公式、诱导公式在三角形中的应用
【解析】由题意可得tanA+tanB=,tanAtanB=,所以tanC=tan[π-(A+B)]=-tan(A+B)=-=-=-7,故答案为-7.
14.若e1,e2是夹角为60°的两个单位向量,向量a=2e1+e2,则|a|= .
【答案】
【考点】平面向量中数量积与模的求解
【解析】由题意|a|====,故答案为.
4616450397510C
C
3863975393700D
D
4203700693420E
E
4003675494030367030049530046005754940303667125494030400050049530015.如图,在等腰梯形ABCD中,DC=AB,BC=CD=DA,DE⊥AC于点E,如果选择向量与作基底,则可用该基底表示为 .
4933950298450B
B
3533775297180A
A
367030099060
【答案】+
【考点】平面向量的基本定理的应用
【解析】由题意可得E为AC的中点,所以=+=+=+,故答案为+.
16.公元前6世纪,古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图,发现了黄金分割值约为0.618,这一数值也可以表示为m=2sin18°.若m2+n2=4,则= .(用数字作答)
【答案】-
【考点】文化题:三角函数公式化简、三角恒等变换化简求值
【解析】由题意====-,故答案为-.
四、解答题:本题共6小题,共70分。需要写出解答过程,请把答案直接填在答题卡相应位置上.
17.(本小题满分10分)
已知
(1)求实数n的值;
(2)若⊥,求实数m的值.
【考点】平面向量的平行与垂直的条件应用
【解析】
因为m),
所以n),
(1)因为所以可得3×(3+m+n)-m×3=0,解得n=-3;
(2)因为,=+=(4,m-3),
因为⊥,所以所以解得m=±1.
18.(本小题满分12分)
求值:(1);
(2)
【考点】三角恒等变换应用
【解析】
(1)原式=(cos215°+sin215°) (cos215°-sin215°)=cos215°-sin215°=cos30°=;
(2) 原式
19.(本小题满分12分)
已知cos(α-)=-,sin(-β)=,且α∈(,π),β∈(0,).求:
(1);
(2)tan(α+β).
【考点】二倍角公式的应用、给值求值问题:变角(构造角)
【解析】
(1)
∴<α-<π,-<-β<,
∴sin(α-)==
cos(-β)==
]si
=;
(2)
,
∴
20.(本小题满分12分)
3533775594360D
D
4968875594360C
C
3222625693420如图,在平行四边形ABCD中,点E,F,G分别在边AB,AD,BC上,且满足AE=AB,AF=AD,BG=BC,设=a,=b.
3536950990603333750396240480060045720G
G
3181350278130F
F
(1)用a,b表示,;
3467100184150E
E
4467225118110B
B
306705099060A
A
(2)若EF⊥EG,=2ab,求角A的值.
【考点】平面向量的数量积应用
【解析】
(1)由平面向量的线性运算可知=-=-=b-a,
=+=+=b+a,
(2)由题意,因为EF⊥EG,所以=(b-a)(b+a)=(b-a)(b+a)=(|b|2-|a|2)=0,解得|a|=|b|,
所以=a(b+a)=ab+|a|2=2ab,
化简得2ab=|a|2,即2|a||b|cosA=|a||a|=|a||b|,
所以cosA=,
又因A∈(0,π),所以A=.
21.(本小题满分12分)
已知向量a=(sinx,),b=(cosx,-1).
(1)当a∥b时,求tan2x的值;
(2)设函数f(x)=2(a+b)b,且x∈(0,),求f(x)的最大值以及对应的x的值.
【考点】平面向量中平行的坐标运算、正切的二倍角公式运用、三角恒等变换与三角函数的图象与性质综合运用
【解析】
(1)因为a//b,所以.
因此tan2x===-.
(2)由题意f(x)=2(a+b)b=2
因此f(x)的最大值为
由x∈(0,),得此时.
22.(本小题满分12分)
在平面直角坐标系中,O为坐标原点,已知向量a=(-1,2),点A(8,0),B(n,t),C(ksinθ,t),(0≤θ≤).
(1)若⊥a,且||=||,求向量;
(2)若向量与向量a共线,当k>4,且tsinθ取得最大值4时,求.
【考点】三角函数与平面向量综合应用、三角函数的图象与性质及变换应用
【解析】
(1)由题设知
因为所以8-n+2t=0,
又所以,解得t=±8;
当t=8时,n=24;当t=-8时,n=-8.
所以,或.
(2)由题设知
因为与a共线,所以t=-2ksinθ+16,
tsinθ=(-2ksinθ+16)
因为k>4,所以
所以当时,tsinθ取得最大值
由得k=8,此时
所以=(8,0)(4,8)=32.
同课章节目录
