6.4 平面向量的应用 正弦、余弦定理的应用(含解析)
文档属性
| 名称 | 6.4 平面向量的应用 正弦、余弦定理的应用(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 275.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 00:00:00 | ||
图片预览




文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
正弦、余弦定理的应用
一、单选题(共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.2020年5月,《东莞市生活垃圾分类三年行动方案》出台.根据该方案,小明家所在小区设置了两个垃圾回收点A,B,他从自家楼下出发,向正北方向走80米,到达回收点A,再向南偏东60°方向走30米,到达回收点B,则他从回收点B回到自家楼下至少还需走(???
)
A.?50米????????????????????????????????????B.?57米????????????????????????????????????C.?64米????????????????????????????????????D.?70米
2.某公园有一个边长为
的等边三角形花圃,现要在花圃中修一条篱笆,将花圃分成面积相等的两部分,则篱笆的最短长度为(???
)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
3.一辆汽车在一水平的公路上由北向南行驶,在公路右侧有一高山.汽车行驶到A处测得高山在南偏西15°方向上,山顶处的仰角为60°,继续向南行驶
到B处测得高山在南偏西75°方向上,则山高为(???
)
A.?????????????B.?????????????C.?????????????D.?
4.如图所示,
两地之间有一座山,汽车原来从
地到
地需经
地沿折线
行驶,现开通隧道后,汽车可直接沿直线
行驶,已知
,
,
,则隧道开通后,汽车从
地到
地比原来少走(结果精确到
;参考数据:
,
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
5.如图所示,为了测量某一隧道两侧A、B两地间的距离,某同学首先选定了不在直线AB上的一点C(
中∠A、∠B、∠C所对的边分别为a、b、c),然后确定测量方案并测出相关数据,进行计算.现给出如下四种测量方案;①测量∠A,∠C,b;②测量∠A,∠B,∠C;③测量a,b,∠C;④测量∠A,∠B,a,则一定能确定A、B间距离的所有方案的序号为(???
)
A.?①③?????????????????????????????????B.?①③④?????????????????????????????????C.?②③④?????????????????????????????????D.?①②④
6.某观察站
与两灯塔
,
的距离分别为3km和5km,测得灯塔
在观察站
北偏西50°,灯塔
在观察站
北偏东70°,则两灯塔
,
间的距离为(???
)
A.?7???????????????????????????????B.?8???????????????????????????????C.????????????????????????????????D.?
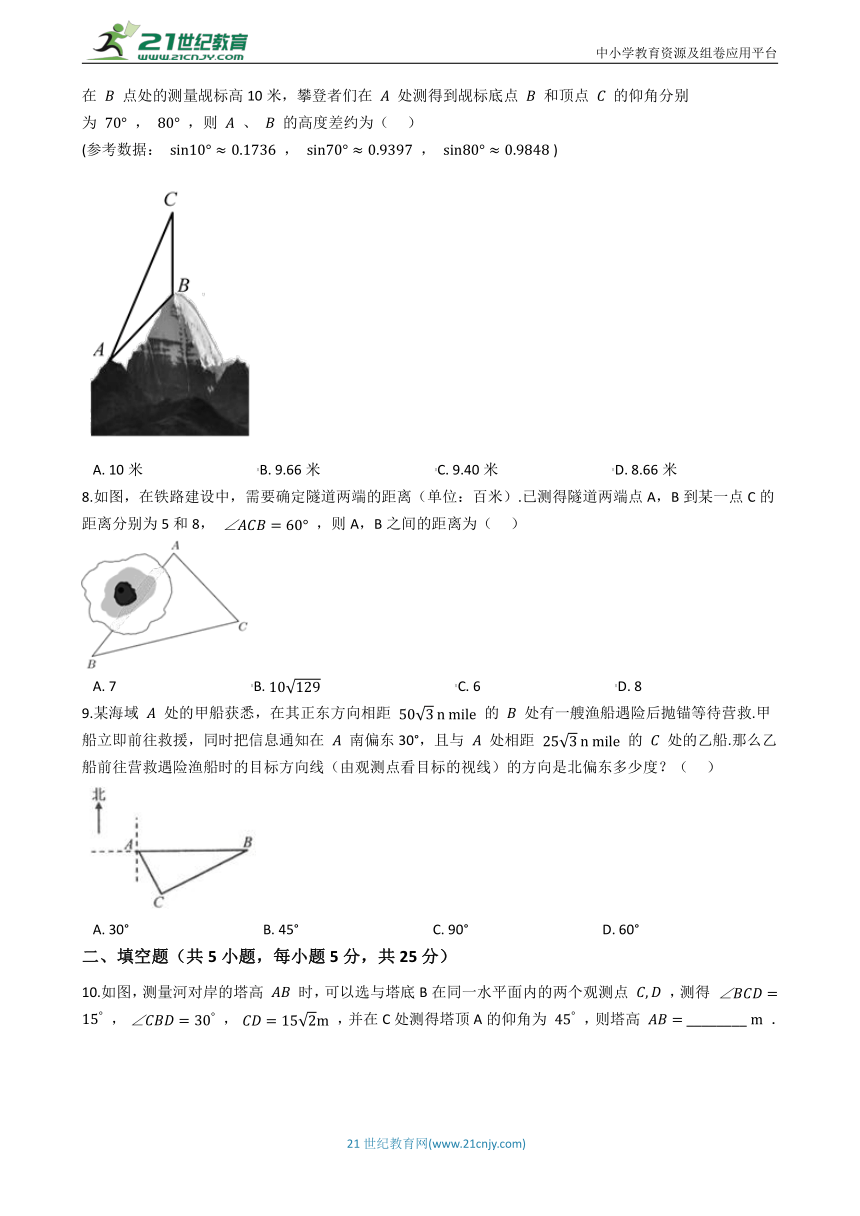
7.为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度,通常采用人工攀登的方式进行,测量人员从山脚开始,直到到达山顶分段测量,最后将所有的高度差累加,得到珠峰的高度,在测量过程中,已知竖立在
点处的测量觇标高10米,攀登者们在
处测得到觇标底点
和顶点
的仰角分别为
,
,则
、
的高度差约为(???
)
(参考数据:
,
,
)
A.?10米?????????????????????????????????B.?9.66米?????????????????????????????????C.?9.40米?????????????????????????????????D.?8.66米
8.如图,在铁路建设中,需要确定隧道两端的距离(单位:百米).已测得隧道两端点A,B到某一点C的距离分别为5和8,
,则A,B之间的距离为(??
?)
A.?7???????????????????????????????????????B.????????????????????????????????????????C.?6???????????????????????????????????????D.?8
9.某海域
处的甲船获悉,在其正东方向相距
的
处有一艘渔船遇险后抛锚等待营救.甲船立即前往救援,同时把信息通知在
南偏东30°,且与
处相距
的
处的乙船.那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度?(???
)
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?90°???????????????????????????????????????D.?60°
二、填空题(共5小题,每小题5分,共25分)
10.如图,测量河对岸的塔高
时,可以选与塔底B在同一水平面内的两个观测点
,测得
,
,
,并在C处测得塔顶A的仰角为
,则塔高
________
.
11.为了响应曲沃中学第三届文化艺术节,了解更多曲沃文化,在申园太子湖西岸测量位于湖中的萱楼的高度
,可以选与萱楼底在同一水平面内的两个点C与D.如图所示,现测得
并在点C测得楼顶的仰角为
,则萱楼的高度
________米.
12.在
中,内角
,
,
的对边分别是
,
,
.若
,且
的面积为
,则
的值为________.
13.
中,角
所对的边分别为
,已知
A=60°,b=2,
,则
________.
14.在
中,已知
,则角B=________.
三、解答题(共5小题,满分50分.解答应写出文字说明、证明过程或演算步骤.)
15.
中内角
所对的边分别为
,
.
(1)求角
;
(2)若
的周长为
,外接圆半径为
,求
的面积.
16.如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130m/min,山路AC长为1260m,经测量,
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
17.如图所示,基站
处获悉:在其正东方向的
处有一艘渔船遇险等待救援,基站
处的相关人员把消息告知在
处的南偏西
的
处的乙船,请乙船前往救援.
(1)若
两地相距10海里,乙船朝北偏东
的方向沿直线前往
处救援,问
两地相距多少海里?
(2)若乙船在海上从
航行到某一点
,请借助两个观察点
,画出草图,为乙船上的技术人员设计一种能测量
两地距离的方法.
18.在
中,角
,
,
所对的边分别是
,
,
,且
.
(1)若
,求角
的大小;
(2)若
,
,求
的面积.
19.小明在东方明珠广播电视塔底端的正东方向上的
处,沿着与电视塔(
)垂直的水平马路
驾驶机动车行驶,以南偏西60°的方向每小时60千米的速度开了15分钟以后,在点
处望见电视塔的底端
在东北方向上,设沿途
处观察电视塔的仰角
,
的最大值为60°.
(1)小明开车从
处出发到
处,几小时后其所在位置观察电视塔的仰角达到最大值60°,约为多少分钟?(分钟保留两位小数)
(2)求东方明珠塔
的高度约为多少米.(保留两位小数)
答案解析部分
一、单选题
1.【答案】
D
【解析】由题意,可知李华的行走路线,如图所示,
由余弦定理可得
,
即他从回收点B回到自家楼下至少还需要走70米.
故答案为:D.
【分析】画出图形,利用余弦定理转化求解即可。
2.【答案】
D
【解析】设等边三角形花圃为
,因为边长为
,
所以
,
设篱笆
的长度为
,
的长为
,
则
,
因为
,
所以
,即
,所以
,
在
中,由余弦定理可得:
,
即
由基本不等式可得
,
当且仅当
即
时,篱笆长
取得最小值为
,
故答案为:D
【分析】根据题意设出篱笆
的长度为
,
的长为
求出两个三角形的面积令由此得到再由余弦定理求出关于x的代数式,结合基本不等式即可求出y的最小值。
3.【答案】
C
【解析】如图所示:
设A处到山顶处下方的地面C距离为
,则山高
,
在
中,
,
,
,
由正弦定理,得
,
,
所以
,
所以山高为:
,
故答案为:C。
【分析】利用实际问题的已知条件结合正弦定理,从而求出山高。
4.【答案】
A
【解析】
,
,
由正弦定理得
,
.
故答案为:A.
【分析】由已知得
,利用正弦定理求出
BC,AB,即可求解.
5.【答案】
B
【解析】对①:由
,可求得
,再根据正弦定理
,求得AB即可;
对②:由三个角无法确定三角形,故无法计算
的值;
对③:根据余弦定理
,即可求得
的值;
对④:由
,可求得
,再根据正弦定理
,即可求得
的值.
综上所述:①③④可以求得
AB
.
故答案为:B.
【分析】根据正弦定理以及余弦定理,即可对每个选项进行逐一判断分析,作出选择.
6.【答案】
A
【解析】根据题意,画草图
,
结合题干条件易知
,
,
,利用余弦定理可得:
,∴
.
故答案为:A.
【分析】画出图形,可知
,利用余弦定理即可求出
的长.
7.【答案】
C
【解析】如图所示,
在
中,由正弦定理可得
,
由
,
,
所以
,
在
中,
.
故答案为:C.
【分析】根据题意由正弦定理代入数值即可求出再由三角形的几何关系计算出结果即可。
8.【答案】
A
【解析】由题意得:
,
由余弦定理得:
,
,
.
故答案为:A
【分析】根据题意得到
,然后利用余弦定理求解.
9.【答案】
D
【解析】解:如图所示,
,则
,
由题意可知,
,
由余弦定理得
,
解得
,
由正弦定理得
,
解得
,
所以
,
故答案为:D
【分析】根据余弦定理求出
,根据正弦定理求出
,从而可得答案
二、填空题
10.【答案】
30
【解析】在△BCD中,∠BCD=15°,∠CBD=30°,
,
∴
=
,∴
=
,
CB=30
×
=30;
中,∠ACB=45°,
∴塔高AB=BC=30m.
故答案为:30.
【分析】结合图形,利用正弦定理与直角三角形的边角关系,即可求出塔高AB的长.
11.【答案】
【解析】设
,
在直角三角形
中,
,则
,
在三角形
中,
,由正弦定理
,
得
,得
,
所以
.
故答案为:
.
【分析】设
,则
,
在三角形
中,由正弦定理可得的结果。
12.【答案】
4
【解析】由正弦定理及
,得
,
所以
①,
又
,所以
,由
的面积为
,得
,
即
,代入①,得
,所以
.
故答案为:4
【分析】由条件结合正弦定理可得
,再利用余弦定理以及角的范围可得
,然后根据三角形的面积公式即可得出答案.
13.【答案】
4
【解析】由面积公式得
,
,
.
【分析】首先根据三角形的面积公式S△ABC=bcsinA代入数值计算出边c的值再由余弦定理a2=
b2
+c2
-
2bccosA代入数值计算出边a的值,然后利用正弦定理=2R代入数值计算出结果即可。
14.【答案】
【解析】根据三角形的正弦定理
,则可知
的三个角所对应的三个边的比
,根据三角形的余弦定理,则有
=
,故
?。
【分析】利用正弦定理的性质推出
的三个角所对应的三个边的比
,再利用余弦定理,从而结合图替换法,从而求出角B的余弦值,再利用三角形中角B的取值范围,从而求出角B的值。
三、解答题
15.【答案】
(1)解:由
得,
,
所以
,
即
,
因为
,
所以
.
由正弦定理得
,
因为
,
所以
,
所以
,
因为
,
所以
.
(2)解:因为
的外接圆半径为
,
所以
,
所以
,
由余弦定理得,
,
所以
,
得
,
所以
的面积
【分析】(1)由正弦定理和三角恒等变换求得
的值,即可得出A的值;
(2)根据正弦定理求得a的值,再利用周长公式和余弦定理求得bc的值,即可求出的面积。
16.【答案】
(1)解:在△ABC中,因为cos
A=
,cos
C=
,
所以sin
A=
,sin
C=
.
从而sin
B=sin[π-(A+C)]=sin(A+C)
=sin
Acos
C+cos
Asin
C=
×
+
×
=
.
由正弦定理
=
,得AB=
×sin
C=
×
=1
040(m).
所以索道AB的长为1
040
m.
(2)解:假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t
m
所以由余弦定理得
d2=(100+50t)2+(130t)2-2×130t×(100+50t)×
=200(37t2-70t+50),
因0≤t≤
,即0≤t≤8,
故当t=
?(min)时,甲、乙两游客距离最短.
【分析】(1)根据正弦定理即可确定出AB的长。
(2)假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t
m?,
由余弦定理可求得?。
17.【答案】
(1)解:如图:
在△
中,
,
,
,
所以
,
由正弦定理得
,
所以
海里,
(2)解:方法为:乙船从
处向正东方向航行
海里到达
处,测得
,
,如图:
在△
中,
,
,
由正弦定理得
,所以
,
在△
中,
,
,
由正弦定理得
,所以
.
【分析】(1)在△
中,
,
,
,根据正弦定理可得结果;(2)乙船从
处向正东方向航行
海里到达
处,测得
,
,利用正弦定理可求得
两地距离.
18.【答案】
(1)解:在
中,因为
,
由正弦定理可得:
,
因为
,
,
可得
,又
,
所以
,
由
,
可得
,即
,
解得:
或
,
又
,得
,所以
(2)解:由(1)知,
,又
,
,
根据余弦定理得,
,
可得
,
即
,解得:
,
,
当
时,
;
当
时,
;
所以
的面积为
或
【分析】(1)利用已知条件结合正弦定理,再利用三角形中角B,C的取值范围,进而求出角B的余弦值,再结合三角形中角B的取值范围,进而求出角B的值,再利用二倍角的余弦公式结合一元二次方程求出角A的余弦值,再利用三角形中角A的取值范围,进而求出角A的值。
(2)
由(1)知,
,又
,
,
再利用余弦定理,进而求出c的值,再利用分类讨论的方法结合三角形面积公式,进而求出三角形
的面积
。
19.【答案】
(1)解:由题知,在
中,
千米,
所以由正弦定理得,
,所以
,
在直角
中,
,因为
不变,所以当
时,
最小,此时
最大,故
,所以
分钟;
(2)解:由(1)知当
时,
最大为
,此时
,
所以
千米,
故东方明珠塔
的高度约为
米.
【分析】(1)利用实际问题的已知条件结合正弦定理,从而求出BC的长,
在直角
中,
,因为
不变,所以当
时,
最小,此时
最大,故
,所以约为
分钟,所在位置观察电视塔的仰角达到最大值60°。
(2)
由(1)知当
时,
最大为
,此时
,
再利用正切函数的定义求出东方明珠塔
大约的高度。
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
正弦、余弦定理的应用
一、单选题(共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.2020年5月,《东莞市生活垃圾分类三年行动方案》出台.根据该方案,小明家所在小区设置了两个垃圾回收点A,B,他从自家楼下出发,向正北方向走80米,到达回收点A,再向南偏东60°方向走30米,到达回收点B,则他从回收点B回到自家楼下至少还需走(???
)
A.?50米????????????????????????????????????B.?57米????????????????????????????????????C.?64米????????????????????????????????????D.?70米
2.某公园有一个边长为
的等边三角形花圃,现要在花圃中修一条篱笆,将花圃分成面积相等的两部分,则篱笆的最短长度为(???
)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
3.一辆汽车在一水平的公路上由北向南行驶,在公路右侧有一高山.汽车行驶到A处测得高山在南偏西15°方向上,山顶处的仰角为60°,继续向南行驶
到B处测得高山在南偏西75°方向上,则山高为(???
)
A.?????????????B.?????????????C.?????????????D.?
4.如图所示,
两地之间有一座山,汽车原来从
地到
地需经
地沿折线
行驶,现开通隧道后,汽车可直接沿直线
行驶,已知
,
,
,则隧道开通后,汽车从
地到
地比原来少走(结果精确到
;参考数据:
,
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
5.如图所示,为了测量某一隧道两侧A、B两地间的距离,某同学首先选定了不在直线AB上的一点C(
中∠A、∠B、∠C所对的边分别为a、b、c),然后确定测量方案并测出相关数据,进行计算.现给出如下四种测量方案;①测量∠A,∠C,b;②测量∠A,∠B,∠C;③测量a,b,∠C;④测量∠A,∠B,a,则一定能确定A、B间距离的所有方案的序号为(???
)
A.?①③?????????????????????????????????B.?①③④?????????????????????????????????C.?②③④?????????????????????????????????D.?①②④
6.某观察站
与两灯塔
,
的距离分别为3km和5km,测得灯塔
在观察站
北偏西50°,灯塔
在观察站
北偏东70°,则两灯塔
,
间的距离为(???
)
A.?7???????????????????????????????B.?8???????????????????????????????C.????????????????????????????????D.?
7.为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度,通常采用人工攀登的方式进行,测量人员从山脚开始,直到到达山顶分段测量,最后将所有的高度差累加,得到珠峰的高度,在测量过程中,已知竖立在
点处的测量觇标高10米,攀登者们在
处测得到觇标底点
和顶点
的仰角分别为
,
,则
、
的高度差约为(???
)
(参考数据:
,
,
)
A.?10米?????????????????????????????????B.?9.66米?????????????????????????????????C.?9.40米?????????????????????????????????D.?8.66米
8.如图,在铁路建设中,需要确定隧道两端的距离(单位:百米).已测得隧道两端点A,B到某一点C的距离分别为5和8,
,则A,B之间的距离为(??
?)
A.?7???????????????????????????????????????B.????????????????????????????????????????C.?6???????????????????????????????????????D.?8
9.某海域
处的甲船获悉,在其正东方向相距
的
处有一艘渔船遇险后抛锚等待营救.甲船立即前往救援,同时把信息通知在
南偏东30°,且与
处相距
的
处的乙船.那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度?(???
)
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?90°???????????????????????????????????????D.?60°
二、填空题(共5小题,每小题5分,共25分)
10.如图,测量河对岸的塔高
时,可以选与塔底B在同一水平面内的两个观测点
,测得
,
,
,并在C处测得塔顶A的仰角为
,则塔高
________
.
11.为了响应曲沃中学第三届文化艺术节,了解更多曲沃文化,在申园太子湖西岸测量位于湖中的萱楼的高度
,可以选与萱楼底在同一水平面内的两个点C与D.如图所示,现测得
并在点C测得楼顶的仰角为
,则萱楼的高度
________米.
12.在
中,内角
,
,
的对边分别是
,
,
.若
,且
的面积为
,则
的值为________.
13.
中,角
所对的边分别为
,已知
A=60°,b=2,
,则
________.
14.在
中,已知
,则角B=________.
三、解答题(共5小题,满分50分.解答应写出文字说明、证明过程或演算步骤.)
15.
中内角
所对的边分别为
,
.
(1)求角
;
(2)若
的周长为
,外接圆半径为
,求
的面积.
16.如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130m/min,山路AC长为1260m,经测量,
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
17.如图所示,基站
处获悉:在其正东方向的
处有一艘渔船遇险等待救援,基站
处的相关人员把消息告知在
处的南偏西
的
处的乙船,请乙船前往救援.
(1)若
两地相距10海里,乙船朝北偏东
的方向沿直线前往
处救援,问
两地相距多少海里?
(2)若乙船在海上从
航行到某一点
,请借助两个观察点
,画出草图,为乙船上的技术人员设计一种能测量
两地距离的方法.
18.在
中,角
,
,
所对的边分别是
,
,
,且
.
(1)若
,求角
的大小;
(2)若
,
,求
的面积.
19.小明在东方明珠广播电视塔底端的正东方向上的
处,沿着与电视塔(
)垂直的水平马路
驾驶机动车行驶,以南偏西60°的方向每小时60千米的速度开了15分钟以后,在点
处望见电视塔的底端
在东北方向上,设沿途
处观察电视塔的仰角
,
的最大值为60°.
(1)小明开车从
处出发到
处,几小时后其所在位置观察电视塔的仰角达到最大值60°,约为多少分钟?(分钟保留两位小数)
(2)求东方明珠塔
的高度约为多少米.(保留两位小数)
答案解析部分
一、单选题
1.【答案】
D
【解析】由题意,可知李华的行走路线,如图所示,
由余弦定理可得
,
即他从回收点B回到自家楼下至少还需要走70米.
故答案为:D.
【分析】画出图形,利用余弦定理转化求解即可。
2.【答案】
D
【解析】设等边三角形花圃为
,因为边长为
,
所以
,
设篱笆
的长度为
,
的长为
,
则
,
因为
,
所以
,即
,所以
,
在
中,由余弦定理可得:
,
即
由基本不等式可得
,
当且仅当
即
时,篱笆长
取得最小值为
,
故答案为:D
【分析】根据题意设出篱笆
的长度为
,
的长为
求出两个三角形的面积令由此得到再由余弦定理求出关于x的代数式,结合基本不等式即可求出y的最小值。
3.【答案】
C
【解析】如图所示:
设A处到山顶处下方的地面C距离为
,则山高
,
在
中,
,
,
,
由正弦定理,得
,
,
所以
,
所以山高为:
,
故答案为:C。
【分析】利用实际问题的已知条件结合正弦定理,从而求出山高。
4.【答案】
A
【解析】
,
,
由正弦定理得
,
.
故答案为:A.
【分析】由已知得
,利用正弦定理求出
BC,AB,即可求解.
5.【答案】
B
【解析】对①:由
,可求得
,再根据正弦定理
,求得AB即可;
对②:由三个角无法确定三角形,故无法计算
的值;
对③:根据余弦定理
,即可求得
的值;
对④:由
,可求得
,再根据正弦定理
,即可求得
的值.
综上所述:①③④可以求得
AB
.
故答案为:B.
【分析】根据正弦定理以及余弦定理,即可对每个选项进行逐一判断分析,作出选择.
6.【答案】
A
【解析】根据题意,画草图
,
结合题干条件易知
,
,
,利用余弦定理可得:
,∴
.
故答案为:A.
【分析】画出图形,可知
,利用余弦定理即可求出
的长.
7.【答案】
C
【解析】如图所示,
在
中,由正弦定理可得
,
由
,
,
所以
,
在
中,
.
故答案为:C.
【分析】根据题意由正弦定理代入数值即可求出再由三角形的几何关系计算出结果即可。
8.【答案】
A
【解析】由题意得:
,
由余弦定理得:
,
,
.
故答案为:A
【分析】根据题意得到
,然后利用余弦定理求解.
9.【答案】
D
【解析】解:如图所示,
,则
,
由题意可知,
,
由余弦定理得
,
解得
,
由正弦定理得
,
解得
,
所以
,
故答案为:D
【分析】根据余弦定理求出
,根据正弦定理求出
,从而可得答案
二、填空题
10.【答案】
30
【解析】在△BCD中,∠BCD=15°,∠CBD=30°,
,
∴
=
,∴
=
,
CB=30
×
=30;
中,∠ACB=45°,
∴塔高AB=BC=30m.
故答案为:30.
【分析】结合图形,利用正弦定理与直角三角形的边角关系,即可求出塔高AB的长.
11.【答案】
【解析】设
,
在直角三角形
中,
,则
,
在三角形
中,
,由正弦定理
,
得
,得
,
所以
.
故答案为:
.
【分析】设
,则
,
在三角形
中,由正弦定理可得的结果。
12.【答案】
4
【解析】由正弦定理及
,得
,
所以
①,
又
,所以
,由
的面积为
,得
,
即
,代入①,得
,所以
.
故答案为:4
【分析】由条件结合正弦定理可得
,再利用余弦定理以及角的范围可得
,然后根据三角形的面积公式即可得出答案.
13.【答案】
4
【解析】由面积公式得
,
,
.
【分析】首先根据三角形的面积公式
b2
+c2
-
2bccosA代入数值计算出边a的值,然后利用正弦定理
14.【答案】
【解析】根据三角形的正弦定理
,则可知
的三个角所对应的三个边的比
,根据三角形的余弦定理,则有
=
,故
?。
【分析】利用正弦定理的性质推出
的三个角所对应的三个边的比
,再利用余弦定理,从而结合图替换法,从而求出角B的余弦值,再利用三角形中角B的取值范围,从而求出角B的值。
三、解答题
15.【答案】
(1)解:由
得,
,
所以
,
即
,
因为
,
所以
.
由正弦定理得
,
因为
,
所以
,
所以
,
因为
,
所以
.
(2)解:因为
的外接圆半径为
,
所以
,
所以
,
由余弦定理得,
,
所以
,
得
,
所以
的面积
【分析】(1)由正弦定理和三角恒等变换求得
的值,即可得出A的值;
(2)根据正弦定理求得a的值,再利用周长公式和余弦定理求得bc的值,即可求出的面积。
16.【答案】
(1)解:在△ABC中,因为cos
A=
,cos
C=
,
所以sin
A=
,sin
C=
.
从而sin
B=sin[π-(A+C)]=sin(A+C)
=sin
Acos
C+cos
Asin
C=
×
+
×
=
.
由正弦定理
=
,得AB=
×sin
C=
×
=1
040(m).
所以索道AB的长为1
040
m.
(2)解:假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t
m
所以由余弦定理得
d2=(100+50t)2+(130t)2-2×130t×(100+50t)×
=200(37t2-70t+50),
因0≤t≤
,即0≤t≤8,
故当t=
?(min)时,甲、乙两游客距离最短.
【分析】(1)根据正弦定理即可确定出AB的长。
(2)假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t
m?,
由余弦定理可求得?。
17.【答案】
(1)解:如图:
在△
中,
,
,
,
所以
,
由正弦定理得
,
所以
海里,
(2)解:方法为:乙船从
处向正东方向航行
海里到达
处,测得
,
,如图:
在△
中,
,
,
由正弦定理得
,所以
,
在△
中,
,
,
由正弦定理得
,所以
.
【分析】(1)在△
中,
,
,
,根据正弦定理可得结果;(2)乙船从
处向正东方向航行
海里到达
处,测得
,
,利用正弦定理可求得
两地距离.
18.【答案】
(1)解:在
中,因为
,
由正弦定理可得:
,
因为
,
,
可得
,又
,
所以
,
由
,
可得
,即
,
解得:
或
,
又
,得
,所以
(2)解:由(1)知,
,又
,
,
根据余弦定理得,
,
可得
,
即
,解得:
,
,
当
时,
;
当
时,
;
所以
的面积为
或
【分析】(1)利用已知条件结合正弦定理,再利用三角形中角B,C的取值范围,进而求出角B的余弦值,再结合三角形中角B的取值范围,进而求出角B的值,再利用二倍角的余弦公式结合一元二次方程求出角A的余弦值,再利用三角形中角A的取值范围,进而求出角A的值。
(2)
由(1)知,
,又
,
,
再利用余弦定理,进而求出c的值,再利用分类讨论的方法结合三角形面积公式,进而求出三角形
的面积
。
19.【答案】
(1)解:由题知,在
中,
千米,
所以由正弦定理得,
,所以
,
在直角
中,
,因为
不变,所以当
时,
最小,此时
最大,故
,所以
分钟;
(2)解:由(1)知当
时,
最大为
,此时
,
所以
千米,
故东方明珠塔
的高度约为
米.
【分析】(1)利用实际问题的已知条件结合正弦定理,从而求出BC的长,
在直角
中,
,因为
不变,所以当
时,
最小,此时
最大,故
,所以约为
分钟,所在位置观察电视塔的仰角达到最大值60°。
(2)
由(1)知当
时,
最大为
,此时
,
再利用正切函数的定义求出东方明珠塔
大约的高度。
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
