2020-2021学年 北师大版数学七年级下册单元过关复习测试练习 第三章 变量之间的关系(word版无答案)
文档属性
| 名称 | 2020-2021学年 北师大版数学七年级下册单元过关复习测试练习 第三章 变量之间的关系(word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 305.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 10:38:42 | ||
图片预览

文档简介
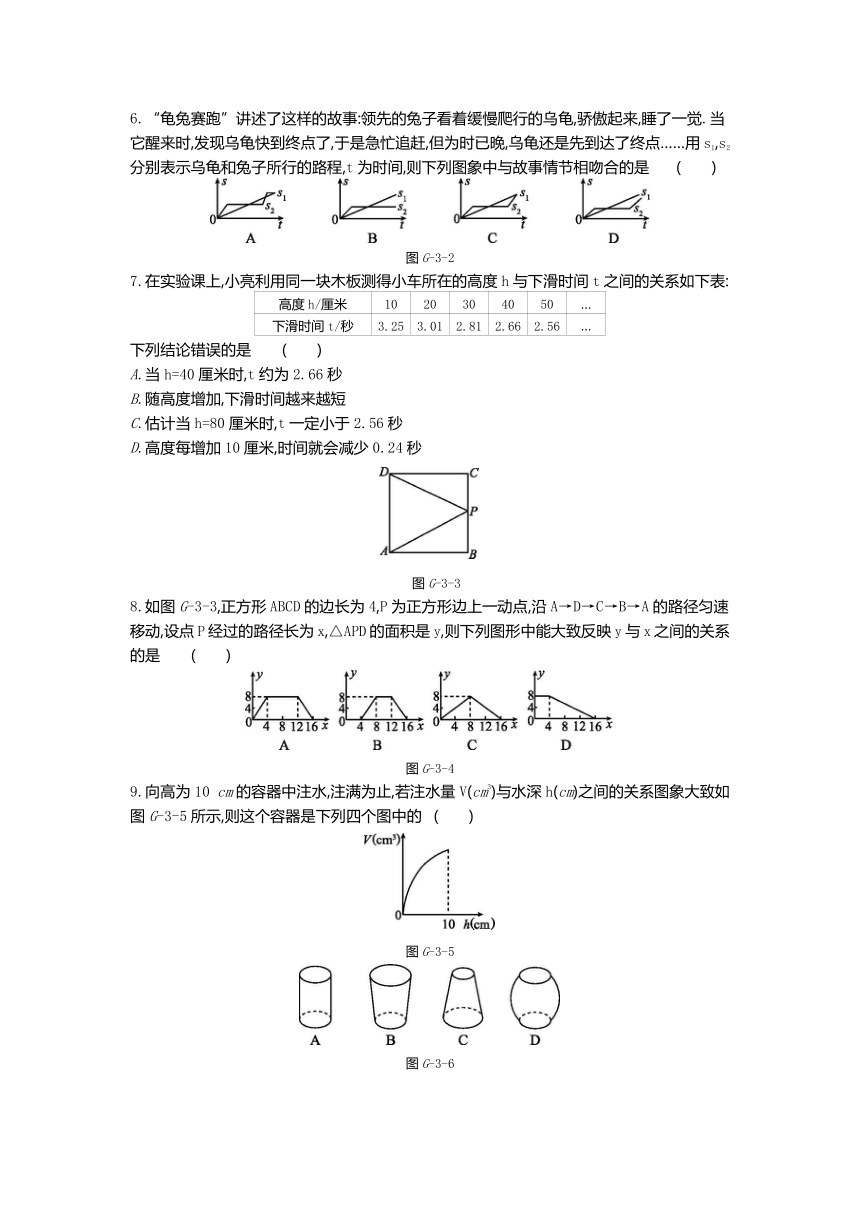
第三章过关测试
(变量之间的关系)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷30分,第Ⅱ卷70分,共100分,考试时间100分钟.
第Ⅰ卷(选择题 共30分)
一、选择题(每题3分,共30分)
1.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化.在这一关系中,自变量是
( )
A.沙漠
B.体温
C.时间
D.骆驼
2.1~6个月的婴儿生长发育得非常快,出生体重为4000克的婴儿,他们的体重y(克)和月龄x(月)之间的关系如下表所示,则6个月大的婴儿的体重为
( )
月龄(月)
1
2
3
4
5
体重(克)
4700
5400
6100
6800
7500
A.7600克
B.7800克
C.8200克
D.8500克
3.某地海拔高度h(千米)与温度T(℃)的关系可用T=21-6h来表示,则该地区海拔高度为2000米的山顶的温度为
( )
A.15
℃
B.9
℃
C.3
℃
D.-11979
℃
4.小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图形中能表示小明的父亲离家的距离与时间的关系的是
( )
图G-3-1
5.下面的表格列出了一个试验的统计数据,表示将皮球从高处落下时,弹跳高度b与下降高度d的关系,下面能表示这种关系的式子是
( )
d
50
80
100
150
b
25
40
50
75
A.b=d2
B.b=
C.b=2d
D.b=d+25
6.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点……用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是
( )
图G-3-2
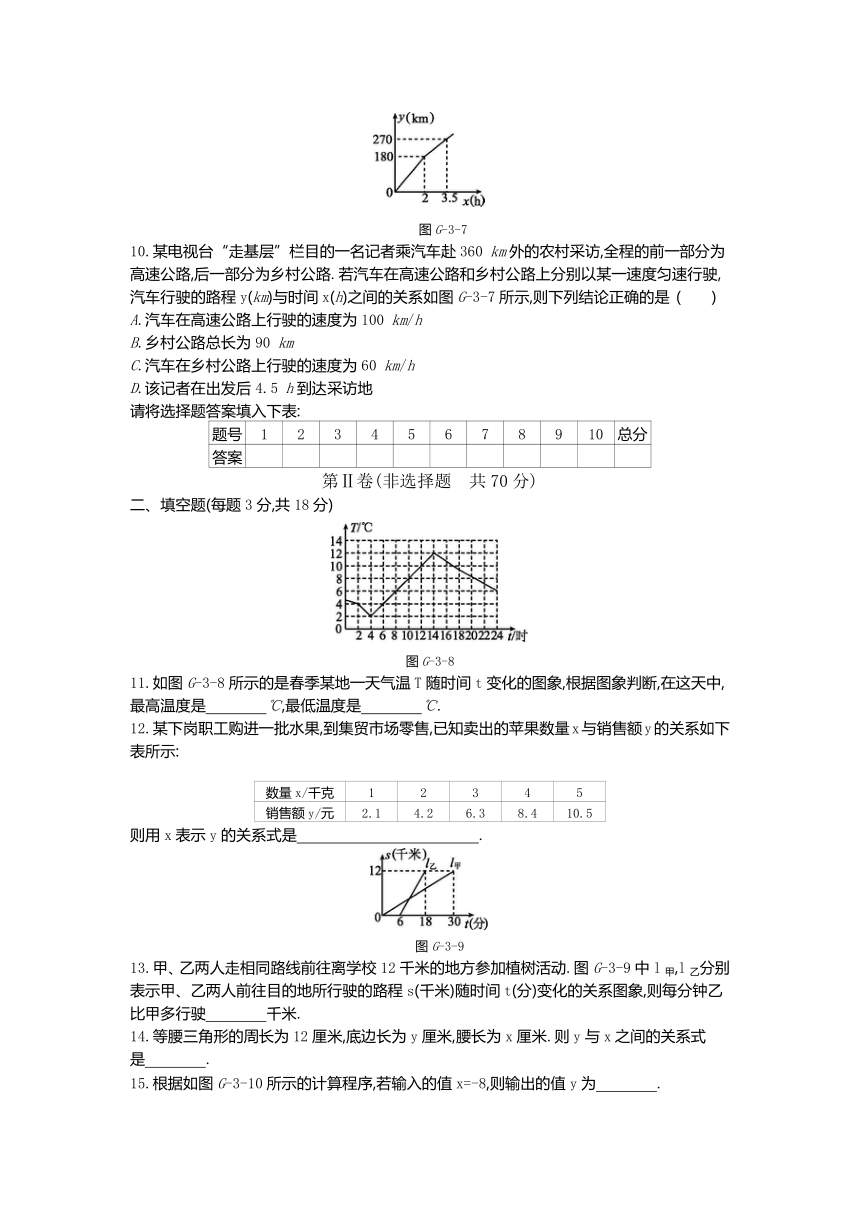
7.在实验课上,小亮利用同一块木板测得小车所在的高度h与下滑时间t之间的关系如下表:
高度h/厘米
10
20
30
40
50
…
下滑时间t/秒
3.25
3.01
2.81
2.66
2.56
…
下列结论错误的是
( )
A.当h=40厘米时,t约为2.66秒
B.随高度增加,下滑时间越来越短
C.估计当h=80厘米时,t一定小于2.56秒
D.高度每增加10厘米,时间就会减少0.24秒
图G-3-3
8.如图G-3-3,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A的路径匀速移动,设点P经过的路径长为x,△APD的面积是y,则下列图形中能大致反映y与x之间的关系的是
( )
图G-3-4
9.向高为10
cm的容器中注水,注满为止,若注水量V(cm3)与水深h(cm)之间的关系图象大致如图G-3-5所示,则这个容器是下列四个图中的
( )
图G-3-5
图G-3-6
图G-3-7
10.某电视台“走基层”栏目的一名记者乘汽车赴360
km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(km)与时间x(h)之间的关系如图G-3-7所示,则下列结论正确的是
( )
A.汽车在高速公路上行驶的速度为100
km/h
B.乡村公路总长为90
km
C.汽车在乡村公路上行驶的速度为60
km/h
D.该记者在出发后4.5
h到达采访地
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷(非选择题 共70分)
二、填空题(每题3分,共18分)
图G-3-8
11.如图G-3-8所示的是春季某地一天气温T随时间t变化的图象,根据图象判断,在这天中,最高温度是 ℃,最低温度是 ℃.?
12.某下岗职工购进一批水果,到集贸市场零售,已知卖出的苹果数量x与销售额y的关系如下表所示:
数量x/千克
1
2
3
4
5
销售额y/元
2.1
4.2
6.3
8.4
10.5
则用x表示y的关系式是 .?
图G-3-9
13.甲、乙两人走相同路线前往离学校12千米的地方参加植树活动.图G-3-9中l甲,l乙分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的关系图象,则每分钟乙比甲多行驶 千米.?
14.等腰三角形的周长为12厘米,底边长为y厘米,腰长为x厘米.则y与x之间的关系式是 .?
15.根据如图G-3-10所示的计算程序,若输入的值x=-8,则输出的值y为 .?
图G-3-10
图G-3-11
16.如图G-3-11(1),在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果图(2)表示y与x之间的关系,则当x=9时,点R应运动到 处.?
三、解答题(共52分)
17.(6分)一天之中不同时刻海水的深度是不同的,如图G-3-12是某港口从0时到12时的水深情况,结合图象回答下列问题:
(1)图中描述了哪两个变量之间的关系?其中自变量是什么,因变量是什么?
(2)大约什么时刻港口的水最深?深度约是多少?
(3)在什么时间范围内,水深在增加?在什么时间范围内,水深在减少?
图G-3-12
18.(6分)高空的气温与距地面的高度有关,某地地面气温为24
℃,且已知离地面距离每升高1
km,气温下降6
℃.
(1)写出该地空中气温T(℃)与高度h(km)之间的关系式;
(2)求距地面3
km处的气温T;
(3)求气温为-6
℃处距地面的高度h.
19.(6分)如图G-3-13所示,圆柱的高是4
cm,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
(1)在这个变化过程中,自变量是 ,因变量是 ;?
(2)求圆柱的体积V与底面半径r之间的关系式;
(3)当圆柱的底面半径由2
cm变化到8
cm时,圆柱的体积由 cm3变化到 cm3.?
图G-3-13
20.(6分)某私营企业现在年产值是30万元,计划以后每年增加15万元.
(1)写出年产值y(万元)与年数x(年)之间的关系式;
(2)用表格表示当x从0到6(每次增加1)时y的对应值;
(3)求10年后的年产值.
21.(6分)星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分)之间的关系图象如图G-3-14所示.根据图象回答下列问题.
(1)小明家离图书馆的距离是多少千米?
(2)小明在图书馆看书的时间为几小时?
(3)小明去图书馆时的速度是多少千米/时?
图G-3-14
22.(6分)某剧院观众席的座位为扇形,且按下列方式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
23.(10分)如图G-3-15是甲、乙两人在同一地点出发后,路程随时间变化的图象.
图G-3-15
(1)此变化过程中, 是自变量, 是因变量;?
(2)甲的速度 (填“大于”“等于”或“小于”)乙的速度;?
(3)路程为150千米时,甲行驶了 小时,乙行驶了 小时.?
(4)9时甲在乙的 (填“前面”“后面”或“相同位置”);?
(5)乙比甲先走了3小时,对吗? .?
24.(6分)图G-3-16①,②分别反映的是孪生兄弟小明与小强从家到劳动公园的行进过程中,离家的距离s与时间t之间的关系图象.请根据图象所提供的信息解答下列问题.
(1)当小强出发的时候,小明此时距离公园 km;?
(2)小强何时与小明第一次相遇?
(3)小强出发后,在什么时间内比小明距离公园更近?
图G-3-16
(变量之间的关系)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷30分,第Ⅱ卷70分,共100分,考试时间100分钟.
第Ⅰ卷(选择题 共30分)
一、选择题(每题3分,共30分)
1.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化.在这一关系中,自变量是
( )
A.沙漠
B.体温
C.时间
D.骆驼
2.1~6个月的婴儿生长发育得非常快,出生体重为4000克的婴儿,他们的体重y(克)和月龄x(月)之间的关系如下表所示,则6个月大的婴儿的体重为
( )
月龄(月)
1
2
3
4
5
体重(克)
4700
5400
6100
6800
7500
A.7600克
B.7800克
C.8200克
D.8500克
3.某地海拔高度h(千米)与温度T(℃)的关系可用T=21-6h来表示,则该地区海拔高度为2000米的山顶的温度为
( )
A.15
℃
B.9
℃
C.3
℃
D.-11979
℃
4.小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图形中能表示小明的父亲离家的距离与时间的关系的是
( )
图G-3-1
5.下面的表格列出了一个试验的统计数据,表示将皮球从高处落下时,弹跳高度b与下降高度d的关系,下面能表示这种关系的式子是
( )
d
50
80
100
150
b
25
40
50
75
A.b=d2
B.b=
C.b=2d
D.b=d+25
6.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点……用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是
( )
图G-3-2
7.在实验课上,小亮利用同一块木板测得小车所在的高度h与下滑时间t之间的关系如下表:
高度h/厘米
10
20
30
40
50
…
下滑时间t/秒
3.25
3.01
2.81
2.66
2.56
…
下列结论错误的是
( )
A.当h=40厘米时,t约为2.66秒
B.随高度增加,下滑时间越来越短
C.估计当h=80厘米时,t一定小于2.56秒
D.高度每增加10厘米,时间就会减少0.24秒
图G-3-3
8.如图G-3-3,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A的路径匀速移动,设点P经过的路径长为x,△APD的面积是y,则下列图形中能大致反映y与x之间的关系的是
( )
图G-3-4
9.向高为10
cm的容器中注水,注满为止,若注水量V(cm3)与水深h(cm)之间的关系图象大致如图G-3-5所示,则这个容器是下列四个图中的
( )
图G-3-5
图G-3-6
图G-3-7
10.某电视台“走基层”栏目的一名记者乘汽车赴360
km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(km)与时间x(h)之间的关系如图G-3-7所示,则下列结论正确的是
( )
A.汽车在高速公路上行驶的速度为100
km/h
B.乡村公路总长为90
km
C.汽车在乡村公路上行驶的速度为60
km/h
D.该记者在出发后4.5
h到达采访地
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷(非选择题 共70分)
二、填空题(每题3分,共18分)
图G-3-8
11.如图G-3-8所示的是春季某地一天气温T随时间t变化的图象,根据图象判断,在这天中,最高温度是 ℃,最低温度是 ℃.?
12.某下岗职工购进一批水果,到集贸市场零售,已知卖出的苹果数量x与销售额y的关系如下表所示:
数量x/千克
1
2
3
4
5
销售额y/元
2.1
4.2
6.3
8.4
10.5
则用x表示y的关系式是 .?
图G-3-9
13.甲、乙两人走相同路线前往离学校12千米的地方参加植树活动.图G-3-9中l甲,l乙分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的关系图象,则每分钟乙比甲多行驶 千米.?
14.等腰三角形的周长为12厘米,底边长为y厘米,腰长为x厘米.则y与x之间的关系式是 .?
15.根据如图G-3-10所示的计算程序,若输入的值x=-8,则输出的值y为 .?
图G-3-10
图G-3-11
16.如图G-3-11(1),在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果图(2)表示y与x之间的关系,则当x=9时,点R应运动到 处.?
三、解答题(共52分)
17.(6分)一天之中不同时刻海水的深度是不同的,如图G-3-12是某港口从0时到12时的水深情况,结合图象回答下列问题:
(1)图中描述了哪两个变量之间的关系?其中自变量是什么,因变量是什么?
(2)大约什么时刻港口的水最深?深度约是多少?
(3)在什么时间范围内,水深在增加?在什么时间范围内,水深在减少?
图G-3-12
18.(6分)高空的气温与距地面的高度有关,某地地面气温为24
℃,且已知离地面距离每升高1
km,气温下降6
℃.
(1)写出该地空中气温T(℃)与高度h(km)之间的关系式;
(2)求距地面3
km处的气温T;
(3)求气温为-6
℃处距地面的高度h.
19.(6分)如图G-3-13所示,圆柱的高是4
cm,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
(1)在这个变化过程中,自变量是 ,因变量是 ;?
(2)求圆柱的体积V与底面半径r之间的关系式;
(3)当圆柱的底面半径由2
cm变化到8
cm时,圆柱的体积由 cm3变化到 cm3.?
图G-3-13
20.(6分)某私营企业现在年产值是30万元,计划以后每年增加15万元.
(1)写出年产值y(万元)与年数x(年)之间的关系式;
(2)用表格表示当x从0到6(每次增加1)时y的对应值;
(3)求10年后的年产值.
21.(6分)星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分)之间的关系图象如图G-3-14所示.根据图象回答下列问题.
(1)小明家离图书馆的距离是多少千米?
(2)小明在图书馆看书的时间为几小时?
(3)小明去图书馆时的速度是多少千米/时?
图G-3-14
22.(6分)某剧院观众席的座位为扇形,且按下列方式设置:
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
23.(10分)如图G-3-15是甲、乙两人在同一地点出发后,路程随时间变化的图象.
图G-3-15
(1)此变化过程中, 是自变量, 是因变量;?
(2)甲的速度 (填“大于”“等于”或“小于”)乙的速度;?
(3)路程为150千米时,甲行驶了 小时,乙行驶了 小时.?
(4)9时甲在乙的 (填“前面”“后面”或“相同位置”);?
(5)乙比甲先走了3小时,对吗? .?
24.(6分)图G-3-16①,②分别反映的是孪生兄弟小明与小强从家到劳动公园的行进过程中,离家的距离s与时间t之间的关系图象.请根据图象所提供的信息解答下列问题.
(1)当小强出发的时候,小明此时距离公园 km;?
(2)小强何时与小明第一次相遇?
(3)小强出发后,在什么时间内比小明距离公园更近?
图G-3-16
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
