2020—2021学年八年级数学人教版下册18.1.1 平行四边形的性质(共26张ppt)
文档属性
| 名称 | 2020—2021学年八年级数学人教版下册18.1.1 平行四边形的性质(共26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 00:00:00 | ||
图片预览






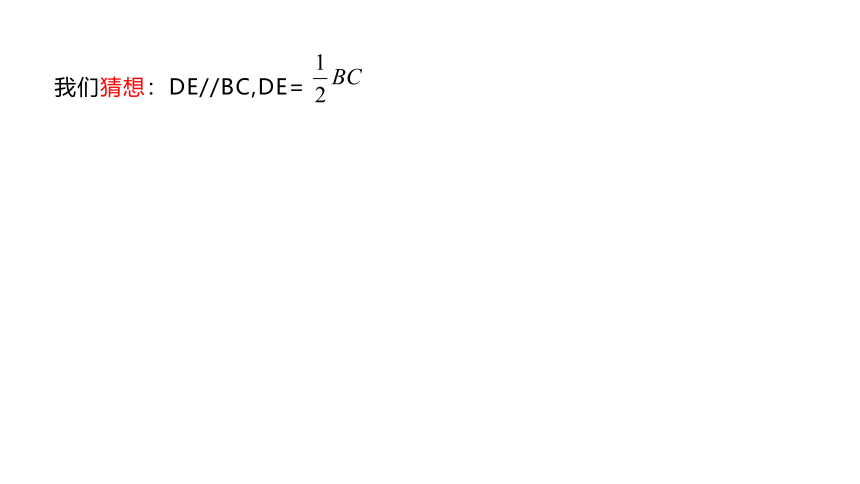
文档简介
(共26张PPT)
三角形的中位线定理
教学目标
1
了解三角形中位线的定义。
2
掌握三角形中位线定理及证明方法。
3
会运用三角形中位线定理进行计算或证明。
教学重难点
三角形中位线定理的证明及应用。
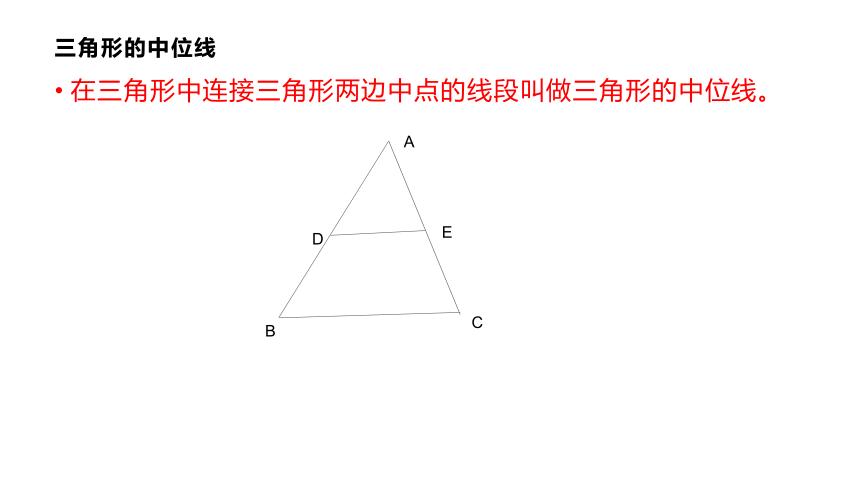
三角形的中位线
在三角形中连接三角形两边中点的线段叫做三角形的中位线。
A
B
C
D
E
思考
根据三角形的中位线定义,请回答一个三角形有几条中位线?
三角形的中位线和中线有区别吗?
由于三角形有三条边,所以一个三角形有三条中位线。
在三角形中连接三角形两边中点的线段叫做三角形的中位线。
在三角形中连接一顶点和它所对边的中点的线段叫做三角形的中线。由于三角形有三条边,所以一个三角形有三条中线。
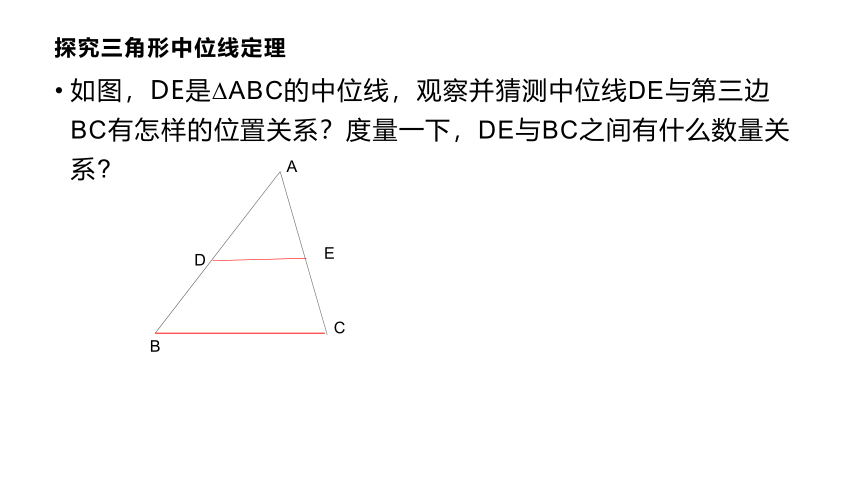
探究三角形中位线定理
如图,DE是?ABC的中位线,观察并猜测中位线DE与第三边BC有怎样的位置关系?度量一下,DE与BC之间有什么数量关系?
A
B
C
D
E
我们猜想:DE//BC,DE=
如图,D,E
分别是?ABC的边AB,AC的中点,求证:DE//BC,且DE=
A
B
C
D
E
分析:本题既要证明两条直线所在的直线平行,又要证明其中一条线段的长等于另一条线段长的一半,将DE延长一倍后,可以将证明DE=
转化为证明延长后的线段与BC相等。又由于E是AC的中点,根据对角线互相平分的四边形是平行四边形构造一个平行四边形,利用平行四边形的性质进行证明。
B
C
A
D
E
F
A
B
C
D
E
→
做相等证平行
A
B
C
D
E
F
做平行证相等
三角形的中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半。
注意:
1.“第三边”含义
2.中位线定理的几何意义
3.理解符号
的含义
4.三角形中位线定理的作用:用于证两线段的位置和数量关系。
“
”
三角形中位线定理的应用
例1见探究
例1及例题1变式训练和例2
A
B
C
E
F
例1
A
F
G
D
E
B
C
例1变式训练
A
D
E
B
C
F
例2
例2
如图
D,E,F是?ABC三边的中点,
①说出图中的所有平行四边形,并选出一个进行证明
②若
=3,则
=
(
)
A
B
C
D
E
F
练习如图,DE是?ABC的中位线,
=12,则
=(
)
A
D
E
B
C
A
B
C
D
F
例3
如图,E,F,G,H是四边形ABCD各边的中点,求证:四边形EFGH是平行四边形。
A
B
C
D
E
F
G
H
A
B
C
D
E
G
F
H
练习
1探究试卷54页第11题
2探究试卷54页第10题
A
B
C
D
E
F
11题
A
E
B
C
D
F
P
10题
3如图,点O是
ABC内任意一点,连接OB,OC,D,G,E,F分别是
AB,AC,OB,OC的中点,求证:四边形DEFG是平行四边形
.
A
B
C
D
G
E
F
O
课堂小结
1三角形中位线的定义及定理
2三角形中位线的性质是证两线段位置关系和数量关系的重要定理,当条件出现中位线或出现一边的中点时,常常要用到中位线定理。
三角形的中位线定理
教学目标
1
了解三角形中位线的定义。
2
掌握三角形中位线定理及证明方法。
3
会运用三角形中位线定理进行计算或证明。
教学重难点
三角形中位线定理的证明及应用。
三角形的中位线
在三角形中连接三角形两边中点的线段叫做三角形的中位线。
A
B
C
D
E
思考
根据三角形的中位线定义,请回答一个三角形有几条中位线?
三角形的中位线和中线有区别吗?
由于三角形有三条边,所以一个三角形有三条中位线。
在三角形中连接三角形两边中点的线段叫做三角形的中位线。
在三角形中连接一顶点和它所对边的中点的线段叫做三角形的中线。由于三角形有三条边,所以一个三角形有三条中线。
探究三角形中位线定理
如图,DE是?ABC的中位线,观察并猜测中位线DE与第三边BC有怎样的位置关系?度量一下,DE与BC之间有什么数量关系?
A
B
C
D
E
我们猜想:DE//BC,DE=
如图,D,E
分别是?ABC的边AB,AC的中点,求证:DE//BC,且DE=
A
B
C
D
E
分析:本题既要证明两条直线所在的直线平行,又要证明其中一条线段的长等于另一条线段长的一半,将DE延长一倍后,可以将证明DE=
转化为证明延长后的线段与BC相等。又由于E是AC的中点,根据对角线互相平分的四边形是平行四边形构造一个平行四边形,利用平行四边形的性质进行证明。
B
C
A
D
E
F
A
B
C
D
E
→
做相等证平行
A
B
C
D
E
F
做平行证相等
三角形的中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半。
注意:
1.“第三边”含义
2.中位线定理的几何意义
3.理解符号
的含义
4.三角形中位线定理的作用:用于证两线段的位置和数量关系。
“
”
三角形中位线定理的应用
例1见探究
例1及例题1变式训练和例2
A
B
C
E
F
例1
A
F
G
D
E
B
C
例1变式训练
A
D
E
B
C
F
例2
例2
如图
D,E,F是?ABC三边的中点,
①说出图中的所有平行四边形,并选出一个进行证明
②若
=3,则
=
(
)
A
B
C
D
E
F
练习如图,DE是?ABC的中位线,
=12,则
=(
)
A
D
E
B
C
A
B
C
D
F
例3
如图,E,F,G,H是四边形ABCD各边的中点,求证:四边形EFGH是平行四边形。
A
B
C
D
E
F
G
H
A
B
C
D
E
G
F
H
练习
1探究试卷54页第11题
2探究试卷54页第10题
A
B
C
D
E
F
11题
A
E
B
C
D
F
P
10题
3如图,点O是
ABC内任意一点,连接OB,OC,D,G,E,F分别是
AB,AC,OB,OC的中点,求证:四边形DEFG是平行四边形
.
A
B
C
D
G
E
F
O
课堂小结
1三角形中位线的定义及定理
2三角形中位线的性质是证两线段位置关系和数量关系的重要定理,当条件出现中位线或出现一边的中点时,常常要用到中位线定理。
