2020-2021学年北师大版数学七年级下册第二章 2.3.1 平行线的性质 课件(共57张PPT)
文档属性
| 名称 | 2020-2021学年北师大版数学七年级下册第二章 2.3.1 平行线的性质 课件(共57张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-05 21:40:35 | ||
图片预览






文档简介
(共57张PPT)
第二章
相交线与平行线
2.3.1
平行线的性质
北师大版数学七年级下册
1.探索并掌握平行线的性质。
2.能用平行线的性质定理进行简单的计算、证明。
3.知道对平行线的性质和判定进行的区别。
学习目标
条件
结论
平行线的判定
同位角相等
内错角相等
同旁内角互补
两直线平行
复习旧知
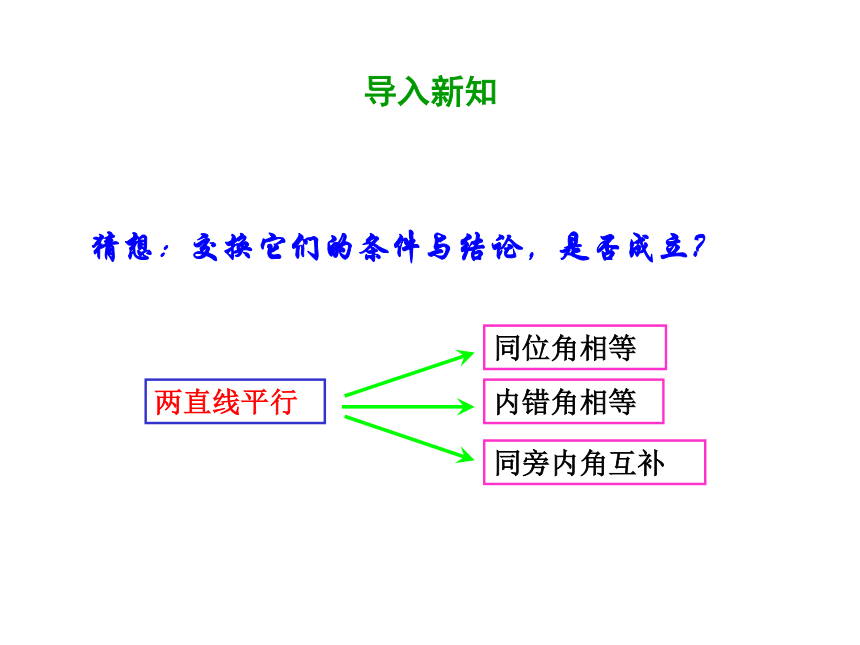
两直线平行
同位角相等
内错角相等
同旁内角互补
猜想:交换它们的条件与结论,是否成立?
导入新知
1
知识点
两条直线平行,同位角相等
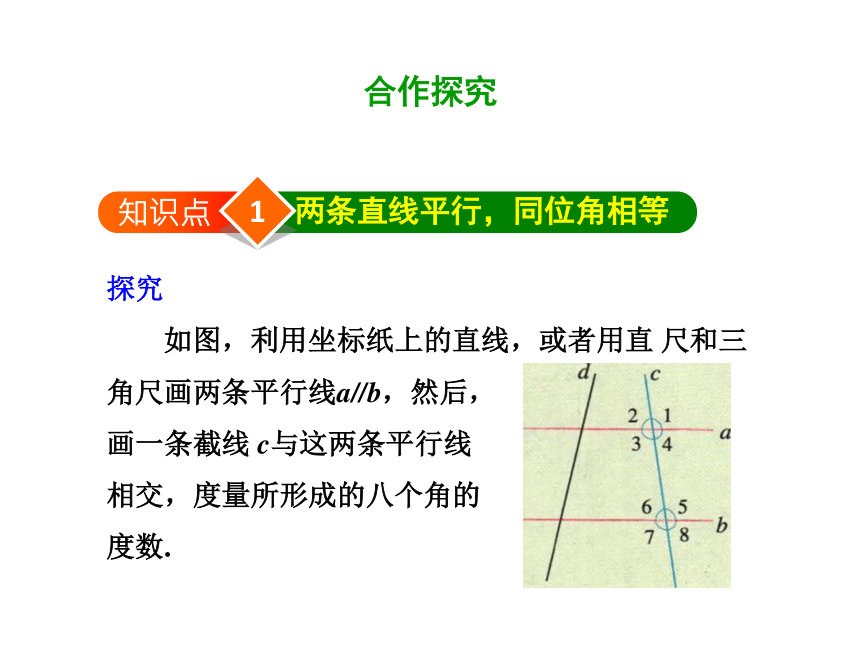
探究
如图,利用坐标纸上的直线,或者用直
尺和三
角尺画两条平行线a//b,然后,
画一条截线
c与这两条平行线
相交,度量所形成的八个角的
度数.
合作探究
两条平行线被第三条直线截得的同位角会具有怎样的数量关系?
性质1
两条平行线被第三条直线
所截,同位角相等.
A
B
P
C
D
E
F
2
1
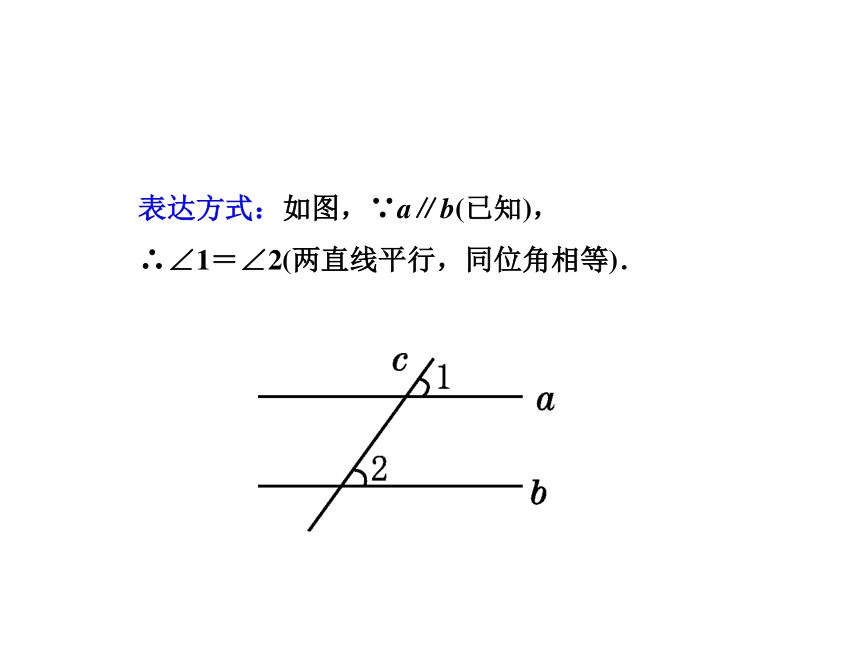
表达方式:如图,∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
例1
如图,直线a∥b,直线c与a,b相交,∠1=70°,
则∠2的大小是( )
A.20°
B.50°
C.70°
D.110°
观察图形可以把求∠2转化为求∠2的对顶角来
解,因为∠2的对顶角与∠1是同位角,而直线
a∥b,所以∠2=∠1=70°.
导引:
C
1
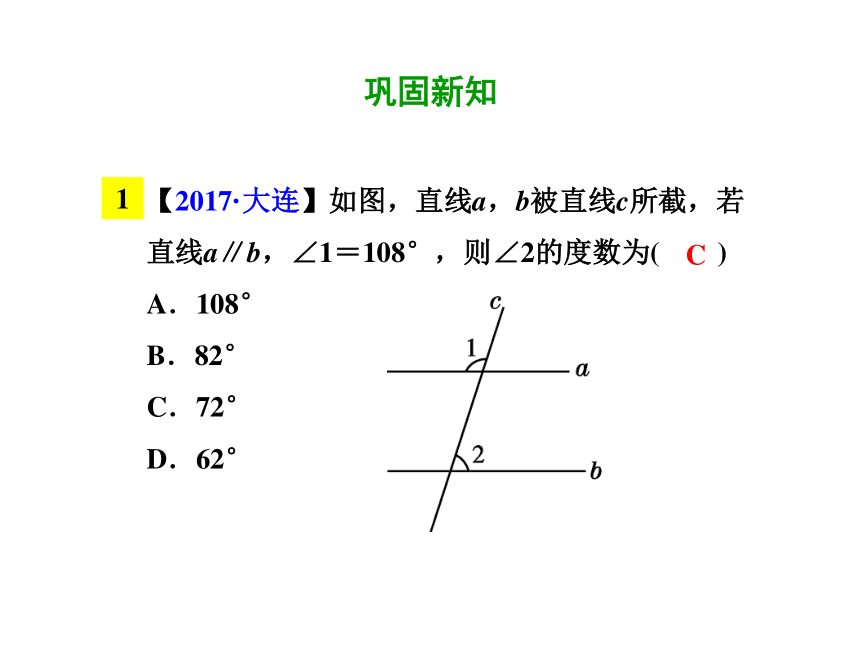
【2017·大连】如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A.108°
B.82°
C.72°
D.62°
C
巩固新知
2
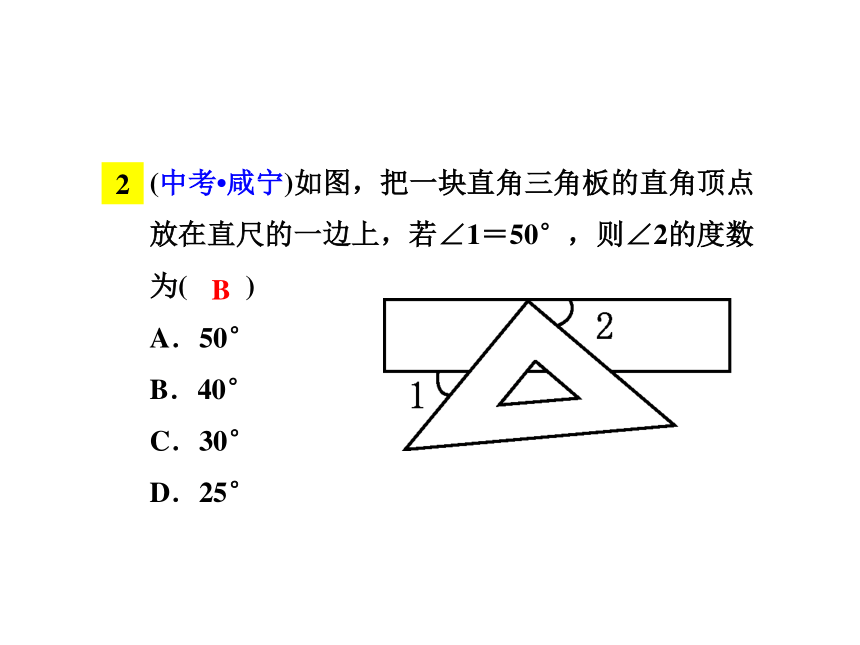
(中考?咸宁)如图,把一块直角三角板的直角顶点
放在直尺的一边上,若∠1=50°,则∠2的度数
为( )
A.50°
B.40°
C.30°
D.25°
B
3
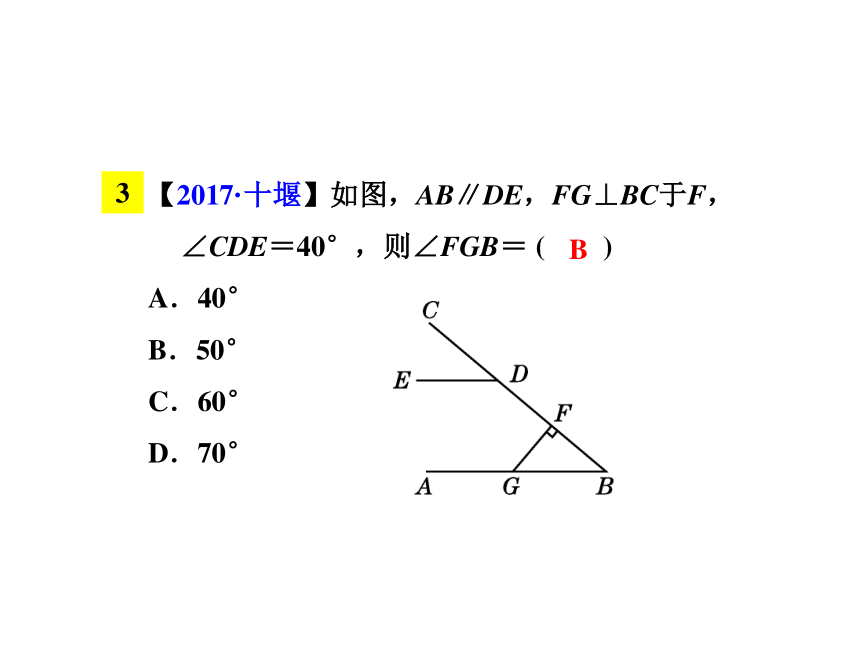
【2017·十堰】如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=
( )
A.40°
B.50°
C.60°
D.70°
B
4
如图,直线a∥b,∠1=60°,∠2=40°,则
∠3等于( )
A.40°
B.60°
C.80°
D.100°
C
5
【2016·朝阳】如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( )
A.40°
B.50°
C.150°
D.140°
D
2
知识点
两条直线平行,内错角相等
性质2
两条平行线被第三条直线
所截,内错角相等.
两条平行线被第三条直线截得的内错角会具有怎样的数量关系?
合作探究
表达方式:如图,
因为a∥b(已知),
所以∠1=∠2(两直线平行,内错角相等).
例2
如图,已知∠B=∠C,AE∥BC,试说明AE平分∠CAD.
要说明AE平分∠CAD,即说明
∠DAE=∠CAE.由于AE∥BC,
根据两直线平行,同位角相等和
内错角相等可知∠DAE=∠B,∠EAC=∠C,
这就将说明∠DAE=∠CAE转化为说明∠B=∠C了.
导引:
因为AE∥BC(已知),
所以∠DAE=∠B(两直线平行,同位角相等),
∠EAC=∠C(两直线平行,内错角相等).
因为∠B=∠C(已知),
所以∠DAE=∠EAC(等量代换).
所以AE平分∠CAD(角平分线的定义).
解:
本题同时运用“两直线平行,同位角相等”和
“两直线平行,内错角相等”提供了一种说明两个
角相等的新思路.
新知小结
1
【2017·安顺】如图,已知a∥b,小华把三角板
的直角顶点放在直线b上.若∠1=40°,则∠2
的度数为( )
A.100°
B.110°
C.120°
D.130°
D
巩固新知
2
【2017·宁波】已知直线m∥n,将一块含30°角的直角三角尺ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在m,n上,若∠1=20°,则∠2的度数为( )
A.20°
B.30°
C.45°
D.50°
D
3
【2017·天门】如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
A.25°
B.35°
C.45°
D.50°
D
3
知识点
两条直线平行,同旁内角互补
“同旁内角”的性质:
性质3
两条平行线被第三条直线
所截,同旁内角互补.
合作探究
表达方式:如图,
因为a∥b(已知),
所以∠1+∠2=180°(两直线平行,同旁内角互补).
例3
如图,如果AB∥DF,DE∥BC,且∠1=65°,那么你能说出∠2,∠3,∠4的度数吗?为什么?
由DE∥BC,可得
∠1=∠4,∠1+∠2=180°;
由DF∥AB,可得∠3=∠2,
从而得∠2,∠3,∠4的度数.
导引:
能.∠2=∠3=115°,∠4=65°.
理由如下:因为DE∥BC(已知),
所以∠4=∠1=65°(两直线平行,内错角相等),
∠2+∠1=180°(两直线平行,同旁内角互补).
所以∠2=180°-∠1=180°-65°=115°.
又因为DF∥AB(已知),
所以∠3=∠2(两直线平行,同位角相等).
所以∠3=115°(等量代换).
解:
(1)求角的度数的基本思路:根据平行线的判定由角
的数量关系得到直线的位置关系,根据平行线的
性质由直线的位置关系得到角的数量关系,通过
上述相互转化,从而找到所求角与已知角之间的
关系.
(2)两直线平行时,应联想到平行线的三个性质,由
两条直线平行的位置关系得到相关角的数量关系,
由角的关系求相应角的度数.
新知小结
1
如图所示,AB∥CD,AC∥BD.
分别找出与∠1相等或互补的角.
如图,与∠1相等的角有∠3,
∠5,∠7,∠9,∠11,∠13,∠15;
与∠1互补的角有∠2,∠4,∠6,∠8,∠10,∠12,∠14,∠16.
解:
巩固新知
2
【2017·邵阳】如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120°
B.100°
C.80°
D.60°
D
3
【2016·深圳】如图,已知a∥b,直角三角尺的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
A.∠2=60°
B.∠3=60°
C.∠4=120°
D.∠5=40°
D
平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
1
知识小结
归纳新知
已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数
是( )
A.50°
B.130°
C.50°或130°
D.不能确定
2
易错小结
D
易错点:利用平行线的性质时易忽视两直线平行这一前提而出错.
本题易忽略利用平行线的性质的前提条件而误用平行线的性质.本题没有说明两直线平行,因此同旁内角的数量关系是不确定的.
B
课后练习
B
A
【答案】B
【答案】D
【答案】C
A
D
D
【答案】B
再见
第二章
相交线与平行线
2.3.1
平行线的性质
北师大版数学七年级下册
1.探索并掌握平行线的性质。
2.能用平行线的性质定理进行简单的计算、证明。
3.知道对平行线的性质和判定进行的区别。
学习目标
条件
结论
平行线的判定
同位角相等
内错角相等
同旁内角互补
两直线平行
复习旧知
两直线平行
同位角相等
内错角相等
同旁内角互补
猜想:交换它们的条件与结论,是否成立?
导入新知
1
知识点
两条直线平行,同位角相等
探究
如图,利用坐标纸上的直线,或者用直
尺和三
角尺画两条平行线a//b,然后,
画一条截线
c与这两条平行线
相交,度量所形成的八个角的
度数.
合作探究
两条平行线被第三条直线截得的同位角会具有怎样的数量关系?
性质1
两条平行线被第三条直线
所截,同位角相等.
A
B
P
C
D
E
F
2
1
表达方式:如图,∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
例1
如图,直线a∥b,直线c与a,b相交,∠1=70°,
则∠2的大小是( )
A.20°
B.50°
C.70°
D.110°
观察图形可以把求∠2转化为求∠2的对顶角来
解,因为∠2的对顶角与∠1是同位角,而直线
a∥b,所以∠2=∠1=70°.
导引:
C
1
【2017·大连】如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A.108°
B.82°
C.72°
D.62°
C
巩固新知
2
(中考?咸宁)如图,把一块直角三角板的直角顶点
放在直尺的一边上,若∠1=50°,则∠2的度数
为( )
A.50°
B.40°
C.30°
D.25°
B
3
【2017·十堰】如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=
( )
A.40°
B.50°
C.60°
D.70°
B
4
如图,直线a∥b,∠1=60°,∠2=40°,则
∠3等于( )
A.40°
B.60°
C.80°
D.100°
C
5
【2016·朝阳】如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( )
A.40°
B.50°
C.150°
D.140°
D
2
知识点
两条直线平行,内错角相等
性质2
两条平行线被第三条直线
所截,内错角相等.
两条平行线被第三条直线截得的内错角会具有怎样的数量关系?
合作探究
表达方式:如图,
因为a∥b(已知),
所以∠1=∠2(两直线平行,内错角相等).
例2
如图,已知∠B=∠C,AE∥BC,试说明AE平分∠CAD.
要说明AE平分∠CAD,即说明
∠DAE=∠CAE.由于AE∥BC,
根据两直线平行,同位角相等和
内错角相等可知∠DAE=∠B,∠EAC=∠C,
这就将说明∠DAE=∠CAE转化为说明∠B=∠C了.
导引:
因为AE∥BC(已知),
所以∠DAE=∠B(两直线平行,同位角相等),
∠EAC=∠C(两直线平行,内错角相等).
因为∠B=∠C(已知),
所以∠DAE=∠EAC(等量代换).
所以AE平分∠CAD(角平分线的定义).
解:
本题同时运用“两直线平行,同位角相等”和
“两直线平行,内错角相等”提供了一种说明两个
角相等的新思路.
新知小结
1
【2017·安顺】如图,已知a∥b,小华把三角板
的直角顶点放在直线b上.若∠1=40°,则∠2
的度数为( )
A.100°
B.110°
C.120°
D.130°
D
巩固新知
2
【2017·宁波】已知直线m∥n,将一块含30°角的直角三角尺ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在m,n上,若∠1=20°,则∠2的度数为( )
A.20°
B.30°
C.45°
D.50°
D
3
【2017·天门】如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
A.25°
B.35°
C.45°
D.50°
D
3
知识点
两条直线平行,同旁内角互补
“同旁内角”的性质:
性质3
两条平行线被第三条直线
所截,同旁内角互补.
合作探究
表达方式:如图,
因为a∥b(已知),
所以∠1+∠2=180°(两直线平行,同旁内角互补).
例3
如图,如果AB∥DF,DE∥BC,且∠1=65°,那么你能说出∠2,∠3,∠4的度数吗?为什么?
由DE∥BC,可得
∠1=∠4,∠1+∠2=180°;
由DF∥AB,可得∠3=∠2,
从而得∠2,∠3,∠4的度数.
导引:
能.∠2=∠3=115°,∠4=65°.
理由如下:因为DE∥BC(已知),
所以∠4=∠1=65°(两直线平行,内错角相等),
∠2+∠1=180°(两直线平行,同旁内角互补).
所以∠2=180°-∠1=180°-65°=115°.
又因为DF∥AB(已知),
所以∠3=∠2(两直线平行,同位角相等).
所以∠3=115°(等量代换).
解:
(1)求角的度数的基本思路:根据平行线的判定由角
的数量关系得到直线的位置关系,根据平行线的
性质由直线的位置关系得到角的数量关系,通过
上述相互转化,从而找到所求角与已知角之间的
关系.
(2)两直线平行时,应联想到平行线的三个性质,由
两条直线平行的位置关系得到相关角的数量关系,
由角的关系求相应角的度数.
新知小结
1
如图所示,AB∥CD,AC∥BD.
分别找出与∠1相等或互补的角.
如图,与∠1相等的角有∠3,
∠5,∠7,∠9,∠11,∠13,∠15;
与∠1互补的角有∠2,∠4,∠6,∠8,∠10,∠12,∠14,∠16.
解:
巩固新知
2
【2017·邵阳】如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120°
B.100°
C.80°
D.60°
D
3
【2016·深圳】如图,已知a∥b,直角三角尺的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
A.∠2=60°
B.∠3=60°
C.∠4=120°
D.∠5=40°
D
平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
1
知识小结
归纳新知
已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数
是( )
A.50°
B.130°
C.50°或130°
D.不能确定
2
易错小结
D
易错点:利用平行线的性质时易忽视两直线平行这一前提而出错.
本题易忽略利用平行线的性质的前提条件而误用平行线的性质.本题没有说明两直线平行,因此同旁内角的数量关系是不确定的.
B
课后练习
B
A
【答案】B
【答案】D
【答案】C
A
D
D
【答案】B
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
