2020-2021学年七年级数学北师大版下册第2章相交线与平行线章末综合优生辅导训练(word版附答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册第2章相交线与平行线章末综合优生辅导训练(word版附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 246.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 13:44:08 | ||
图片预览

文档简介
2021年度北师大版七年级数学下册第2章相交线与平行线章末综合优生辅导训练(附答案)
1.沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反,若汽车第一次是右拐40°,则第二次应该是( )
A.左拐40°
B.左拐50°
C.左拐140°
D.右拐140°
2.如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )
A.∠A=∠C+∠E+∠F
B.∠A+∠E﹣∠C﹣∠F=180°
C.∠A+∠C﹣∠E﹣∠F=180°
D.∠A+∠E+∠C+∠F=360°
3.把一副三角尺放在同一水平桌面上,若它们的两个直角顶点重合,两条斜边平行(如图所示),则∠1=( )
A.75°
B.90°
C.100°
D.105°
4.如图,直线MN∥PQ,点A是MN上一点,∠MAC的角平分线交PQ于点B,若∠1=20°,∠2=116°,则∠3的大小为( )
A.136°
B.138°
C.146°
D.148°
5.将直角三角板按照如图方式摆放,直线a∥b,若∠1=130°,则∠2的度数为( )
A.40°
B.45°
C.50°
D.60°
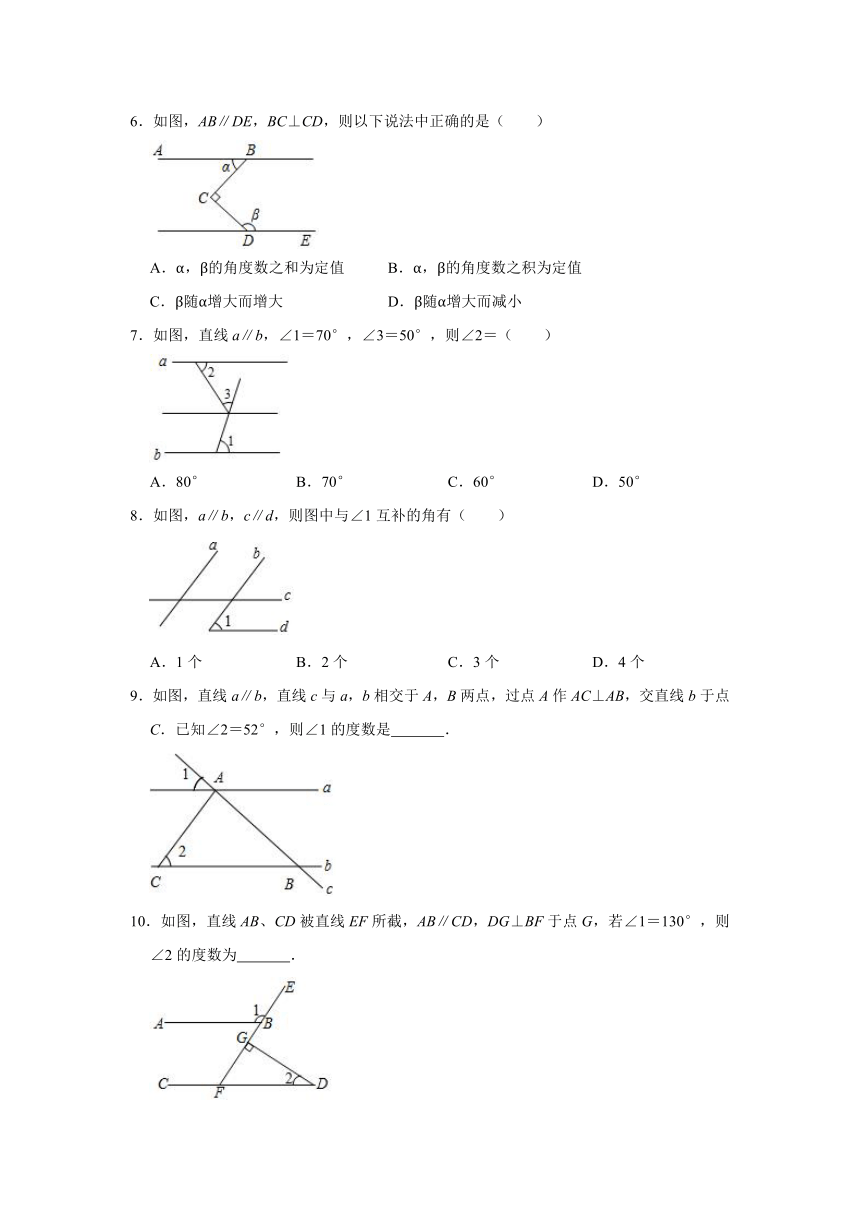
6.如图,AB∥DE,BC⊥CD,则以下说法中正确的是( )
A.α,β的角度数之和为定值
B.α,β的角度数之积为定值
C.β随α增大而增大
D.β随α增大而减小
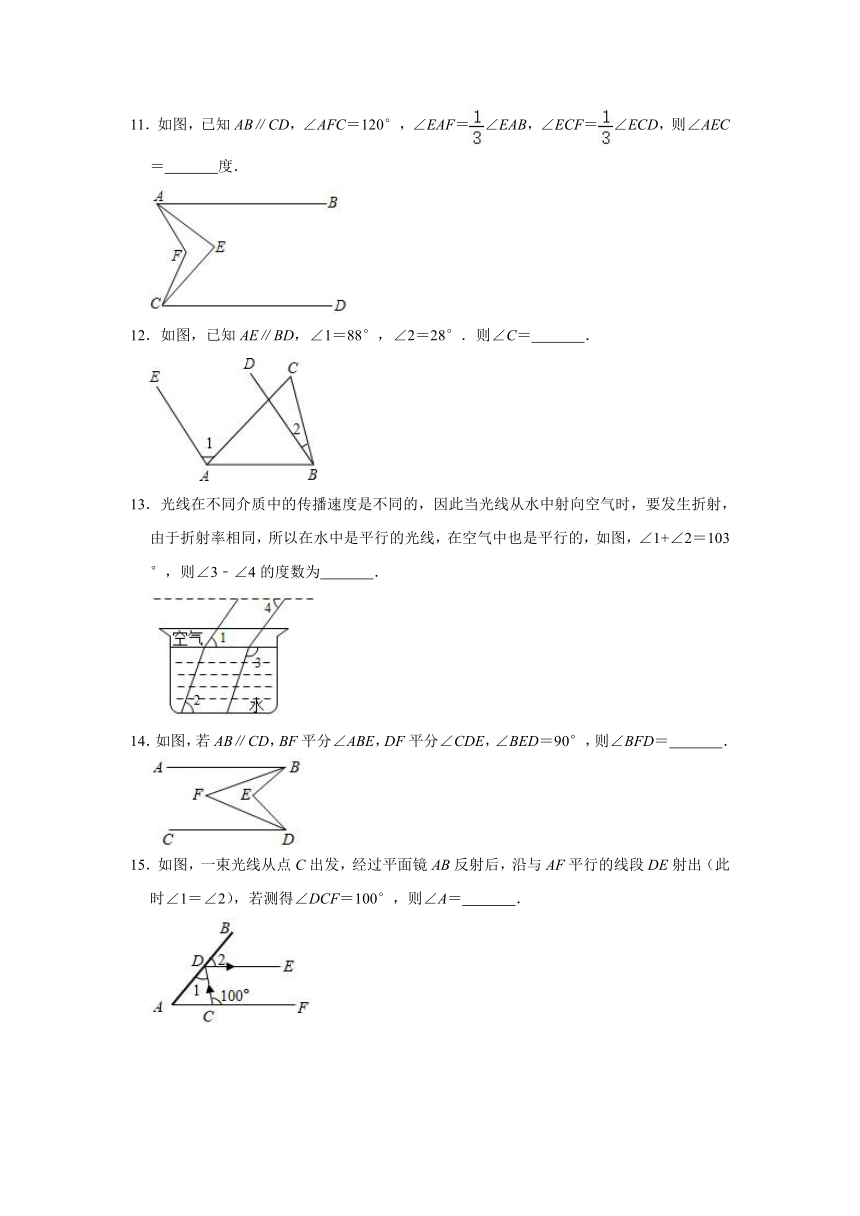
7.如图,直线a∥b,∠1=70°,∠3=50°,则∠2=( )
A.80°
B.70°
C.60°
D.50°
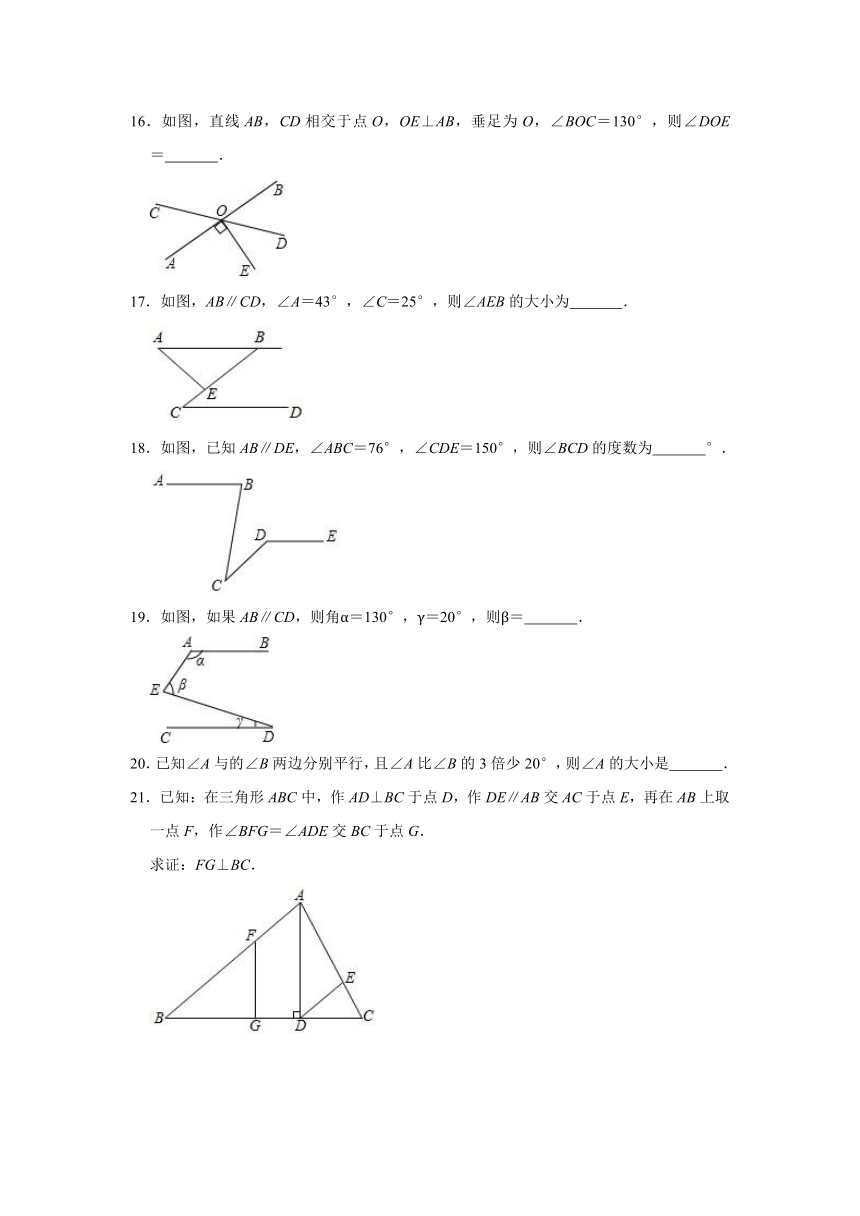
8.如图,a∥b,c∥d,则图中与∠1互补的角有( )
A.1个
B.2个
C.3个
D.4个
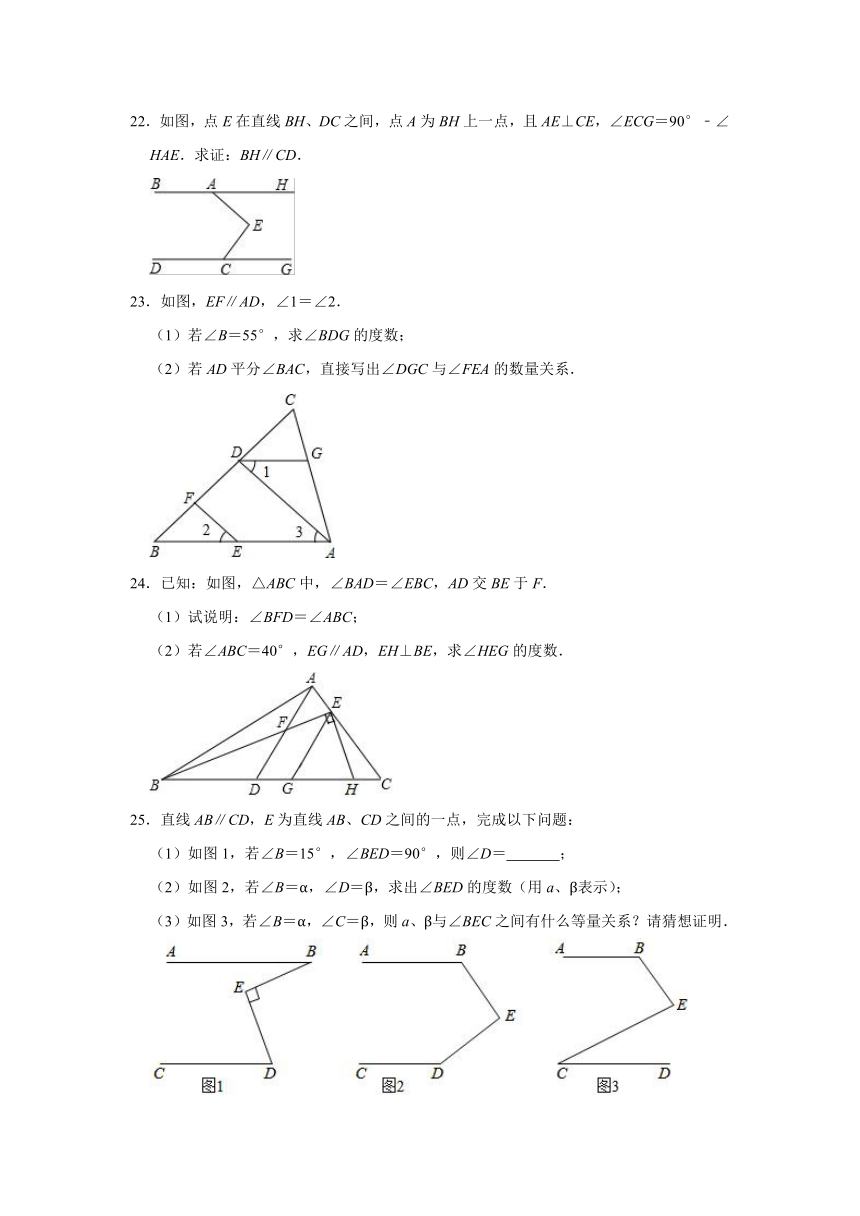
9.如图,直线a∥b,直线c与a,b相交于A,B两点,过点A作AC⊥AB,交直线b于点C.已知∠2=52°,则∠1的度数是
.
10.如图,直线AB、CD被直线EF所截,AB∥CD,DG⊥BF于点G,若∠1=130°,则∠2的度数为
.
11.如图,已知AB∥CD,∠AFC=120°,∠EAF=∠EAB,∠ECF=∠ECD,则∠AEC=
度.
12.如图,已知AE∥BD,∠1=88°,∠2=28°.则∠C=
.
13.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中是平行的光线,在空气中也是平行的,如图,∠1+∠2=103°,则∠3﹣∠4的度数为
.
14.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD=
.
15.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=
.
16.如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOC=130°,则∠DOE=
.
17.如图,AB∥CD,∠A=43°,∠C=25°,则∠AEB的大小为
.
18.如图,已知AB∥DE,∠ABC=76°,∠CDE=150°,则∠BCD的度数为
°.
19.如图,如果AB∥CD,则角α=130°,γ=20°,则β=
.
20.已知∠A与的∠B两边分别平行,且∠A比∠B的3倍少20°,则∠A的大小是
.
21.已知:在三角形ABC中,作AD⊥BC于点D,作DE∥AB交AC于点E,再在AB上取一点F,作∠BFG=∠ADE交BC于点G.
求证:FG⊥BC.
22.如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠ECG=90°﹣∠HAE.求证:BH∥CD.
23.如图,EF∥AD,∠1=∠2.
(1)若∠B=55°,求∠BDG的度数;
(2)若AD平分∠BAC,直接写出∠DGC与∠FEA的数量关系.
24.已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明:∠BFD=∠ABC;
(2)若∠ABC=40°,EG∥AD,EH⊥BE,求∠HEG的度数.
25.直线AB∥CD,E为直线AB、CD之间的一点,完成以下问题:
(1)如图1,若∠B=15°,∠BED=90°,则∠D=
;
(2)如图2,若∠B=α,∠D=β,求出∠BED的度数(用a、β表示);
(3)如图3,若∠B=α,∠C=β,则a、β与∠BEC之间有什么等量关系?请猜想证明.
26.直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点.
(1)若点P在直线CD上,如图①,∠α=50°,则∠2=
°.
(2)若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;
(3)若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由.
27.已知直线AB∥CD,M是直线AB上一点,N是直线CD上一点,点P在AB,CD之间.
(1)如图1,求证:∠BMP+∠DNP=∠MPN;
(2)如图2,NQ⊥CD,MQ⊥MP,若∠PND=30°,∠MPN=100°,直接写出∠MQN的度数.
28.如图,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG=90°,点F在直线AD上,∠AHG=90°.
(1)找出一个角与∠D相等,并说明理由;
(2)如果∠ECF=60°,求∠BCD的度数;
(3)在(2)的条件下,点C(点C不与点B、H重合)从点B出发,沿射线BG的方向运动,其他条件不变,请求出∠BAF的度数.
参考答案
1.解:依照题意画出图形,如图所示.
∵直线l1∥直线l2,
∴∠1+∠2=180°,
∴∠2=180°﹣∠1=180°﹣40°=140°,
∴∠3=∠2=140°,
∴第二次是右拐140°.
故选:D.
2.解:如图,过E作EG∥AB,EG交FC于点O,
∵AB∥CD,
∴AB∥CD∥EG,
∴∠A+∠AEG=180°,∠C=∠FOG,
∵∠FOG=∠F+∠FEG=∠F+∠FEA+∠AEG,
∴∠A+∠AEG=∠A+∠C﹣(∠F+∠FEA)=180°,
∴∠A+∠C﹣∠F﹣∠E=180°,
故选:C.
3.解:作直线l平行于直角三角板的斜边,
可得:∠2=∠3=45°,∠5=∠4=60°,
故∠1的度数是:45°+60°=105°.
故选:D.
4.解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°﹣116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2﹣∠1=116°﹣20°=96°,
∴∠ADC=180°﹣96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
5.解:延长直角三角板的一边交于直线b,给各角标上序号,则∠4=90°,如图所示,
∵直线a∥b,
∴∠3=∠1=130°.
又∵∠3=∠2+∠4,
即130°=∠2+90°,
∴∠2=130°﹣90°=40°.
故选:A.
6.解:过C点作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠α=∠BCF,∠β+∠DCF=180°,
∵BC⊥CD,
∴∠BCF+∠DCF=90°,
∴∠α+180°﹣∠β=90°,
∴∠β﹣∠α=90°,
∴β随α增大而增大,
故选:C.
7.解:如右图所示,
∵a∥b,
∴∠1=∠4,
∴∠1=70°,
∴∠4=70°,
∵∠3=50°,∠2+∠3+∠4=180°,
∴∠2=180°﹣∠3﹣∠4=180°﹣50°﹣70°=60°,
故选:C.
8.解:∵a∥b,c∥d,
∴∠2=∠3,∠1+∠2=180°,
∴∠1+∠3=180°,
∵∠3=∠4,∠2=∠5,
∴∠1+∠4=180°,∠1+∠5=180°,
故选:D.
9.解:∵直线a∥b,
∴∠1=∠CBA,
∵AC⊥AB,
∴∠2+∠CBA=90°,
∴∠2+∠1=90°,
∵∠2=52°,
∴∠1=38°,
故答案为:38°.
10.解:∵AB∥CD,∠1=130°,
∴∠CFB=∠1=130°,
∴∠BFD=180°﹣∠CFB=180°﹣130°=50°,
∵DG⊥BF,
∴∠DGF=90°,
∴∠2=90°﹣∠BFD=90°﹣50°=40°,
故答案为40°.
11.解:过点E作EM∥AB,过点F作FN∥AB,如图所示.
∵EM∥AB,AB∥CD,
∴EM∥CD,
∴∠AEM=∠EAB,∠CEM=∠ECD.
同理,可得:∠AFN=∠FAB,∠CFN=∠FCD.
又∵∠EAF=∠EAB,∠ECF=∠ECD,
∴∠EAB=∠FAB,∠ECD=∠FCD.
∴∠AEC=∠AEM+∠CEM=∠EAB+∠ECD=(∠FAB+∠FCD)=(∠AFN+∠CFN)=∠AFC=90°.
故答案为:90.
12.解:∵AE∥BD,
∴∠1=∠3=88°,
∵∠3=∠2+∠C,
∴∠C=∠3﹣∠2=88°﹣28°=60°,
故答案为:60°.
13.解:如图,∵AB∥CD,
∴∠5=180°﹣∠2,
∵AC∥BD,
∴∠3=∠5,
∵AE∥BF,
∴∠1=∠6,
∵EF∥AB,
∴∠4=∠6,
∴∠3﹣∠4=180°﹣∠2﹣∠1=180°﹣(∠1+∠2)=77°.
故答案为:77°.
14.解:∵AB∥CD,
∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,
∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠1+∠3=45°,
∵∠5=∠2+∠3,
∴∠5=∠1+∠3=45°,
即∠BFD=45°,
故答案为:45°.
15.解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
16.解:∵∠BOC=130°,
∴∠AOD=130°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠DOE=130°﹣90°=40°
故答案为:40°.
17.解:∵AB∥CD,∠C=25°,
∴∠ABE=∠C=25°,
又∵∠A=43°,
∴∠AEB=180°﹣∠A﹣∠ABE=180°﹣43°﹣25°=112°,
故答案为:112°.
18.解:过点C作CF∥AB,
∵AB∥DE,
∴AB∥DE∥CF,
∴∠ABC=∠BCF,∠CDE+∠DCF=180°,
∵∠ABC=76°,∠CDE=150°,
∴∠BCF=76°,∠DCF=30°,
∴∠BCD=46°,
故答案为:46.
19.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠D=∠FED,
∴∠AEF=180°﹣130°=50°,∠FED=20°,
∴∠AED=∠AEF+∠FED=50°+20°=70°.
即β=70°.
故答案为:70°.
20.解:因为∠A与的∠B两边分别平行,
所以∠A与∠B相等或互补,
因为∠A比∠B的3倍少20°,
所以∠A=3∠B﹣20°,
①当∠A=∠B时,
∠A=3∠A﹣20°,
解得∠A=10°;
②当∠A+∠B=180°时,
∠A=3(180°﹣∠A)﹣20°,
解得∠A=130°.
所以∠A的大小是10°或130°.
故答案为:10°或130°.
21.证明:∵AD⊥BC,
∴∠ADB=90°.
∵DE∥AB,
∴∠BAD=∠ADE,
∵∠BFG=∠ADE,
∴∠BAD=∠BFG,
∴AD∥FG,
∴∠FGB=∠ADB=90°,
∴FG⊥BC.
22.证明:过点E作EF∥BH,
∴∠HAE=∠AEF,
∵AE⊥CE,
∴∠AEC=90°
即∠AEF+∠CEF=90°,
∴∠HAE+∠CEF=90°,
∴∠CEF=90°﹣∠HAE,
∵∠ECG=90°﹣∠HAE,
∴∠CEF=∠ECG,
∴EF∥CD,
∵EF∥BH,
∴BH∥CD.
23.解:(1)∵EF∥AD,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥BA,
∴∠B+∠BDG=180°,
∵∠B=55°,
∴∠BDG=125°;
(2)∠DGC+∠FEA=180°,
理由:∵AD平分∠BAC,
∴∠BAC=2∠3,
由(1)知,DG∥BA,
∴∠CGD=∠BAC,
∴∠CGD=2∠3,
∵EF∥AD,
∴∠FEA+∠3=180°,
∴∠DGC+∠FEA=180°.
24.解:(1)∵∠BFD是△ABF的外角,
∴∠BFD=∠BAD+∠ABF,
∵∠BAD=∠EBC,
∴∠BAD+∠ABF=∠EBC+∠ABF,
即∠BFD=∠ABC;
(2)∵∠ABC=40°,∠BFD=∠ABC,
∴∠BFD=40°,
∵EG∥AD,
∴∠BFD=∠BEG,
∴∠BEG=40°,
∵EH⊥BE,
∴∠BEH=90°,
∴∠HEG=∠BEH﹣∠BEG=50°.
25.解:(1)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为:75°;
(2)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°﹣α﹣β,
故答案为:∠BED=360°﹣α﹣β;
(3)猜想:∠BEC=180°﹣α+β.
证明:过点E作EF∥AB,
则∠BEF=180°﹣∠B=180°﹣α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°﹣α+β.
26.解:①∵AB∥CD,∠α=50°
∴∠2=∠α=50°,
故答案为50;
(2)∠α=∠1+∠2.
证明:过P作PG∥AB,
∵AB∥CD,
∴PG∥AB∥CD,
∴∠2=∠EPG,∠1=∠FPG,
∵∠α=∠EPF=∠EPG+∠FPG,
∴∠α=∠1+∠2;
(3)不成立.
理由:过P作PH∥AB,
∵AB∥CD,
∴PH∥AB∥CD,
∴∠2=∠EPH,∠1=∠FPH,
∵∠α=∠EPF=∠EPH﹣∠FPH,
∴∠α=∠2﹣∠1,
故不成立.
27.(1)证明:过P作PG∥AB,
∵AB∥CD,
∴AB∥CD∥PG,
∴∠BMP=∠MPG,∠GPN=∠PND,
∴∠BMP+∠PND=∠MPG+∠GPN,
∴∠MPN=∠BMP+∠PND;
(2)解:∵NQ⊥CD,MQ⊥MP,
∴∠QMP=∠QND=90°,
∵∠PND=30°,
∴∠QNP=90°﹣30°=60°,
∵∠MPN=100°,
∴∠MQN=360°﹣100°﹣60°﹣90°=110°.
28.解:(1)与∠D相等的角为∠DCG,∠ECF,∠B,
∵AD∥BC,
∴∠D=∠DCG,
∵∠FCG=90°,∠DCE=90°,
∴∠ECF=∠DCG,
∴∠D=∠ECF,
∵AB∥DC,
∴∠DCG=∠B,
∴∠B=∠D,
∴与∠D相等的角为∠DCG,∠ECF,∠B;
(2)∵∠ECF=60°,∠DCE=90°,
∴∠FCD=30°,
又∵∠BCF=90°,
∴∠BCD=30°+90°=120°;
(3)如图,当点C在线段BH上时,点F在DA延长线上,
∠ECF=∠DCG=∠B=60°,
∵AD∥BC,
∴∠BAF=∠B=60°;
如图,当点C在BH延长线上时,点F在线段AD上,
∵∠B=60°,AD∥BC,
∴∠BAF=180°﹣60°=120°.
综上所述,∠BAF的度数为60°或120°
1.沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反,若汽车第一次是右拐40°,则第二次应该是( )
A.左拐40°
B.左拐50°
C.左拐140°
D.右拐140°
2.如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )
A.∠A=∠C+∠E+∠F
B.∠A+∠E﹣∠C﹣∠F=180°
C.∠A+∠C﹣∠E﹣∠F=180°
D.∠A+∠E+∠C+∠F=360°
3.把一副三角尺放在同一水平桌面上,若它们的两个直角顶点重合,两条斜边平行(如图所示),则∠1=( )
A.75°
B.90°
C.100°
D.105°
4.如图,直线MN∥PQ,点A是MN上一点,∠MAC的角平分线交PQ于点B,若∠1=20°,∠2=116°,则∠3的大小为( )
A.136°
B.138°
C.146°
D.148°
5.将直角三角板按照如图方式摆放,直线a∥b,若∠1=130°,则∠2的度数为( )
A.40°
B.45°
C.50°
D.60°
6.如图,AB∥DE,BC⊥CD,则以下说法中正确的是( )
A.α,β的角度数之和为定值
B.α,β的角度数之积为定值
C.β随α增大而增大
D.β随α增大而减小
7.如图,直线a∥b,∠1=70°,∠3=50°,则∠2=( )
A.80°
B.70°
C.60°
D.50°
8.如图,a∥b,c∥d,则图中与∠1互补的角有( )
A.1个
B.2个
C.3个
D.4个
9.如图,直线a∥b,直线c与a,b相交于A,B两点,过点A作AC⊥AB,交直线b于点C.已知∠2=52°,则∠1的度数是
.
10.如图,直线AB、CD被直线EF所截,AB∥CD,DG⊥BF于点G,若∠1=130°,则∠2的度数为
.
11.如图,已知AB∥CD,∠AFC=120°,∠EAF=∠EAB,∠ECF=∠ECD,则∠AEC=
度.
12.如图,已知AE∥BD,∠1=88°,∠2=28°.则∠C=
.
13.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中是平行的光线,在空气中也是平行的,如图,∠1+∠2=103°,则∠3﹣∠4的度数为
.
14.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD=
.
15.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=
.
16.如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOC=130°,则∠DOE=
.
17.如图,AB∥CD,∠A=43°,∠C=25°,则∠AEB的大小为
.
18.如图,已知AB∥DE,∠ABC=76°,∠CDE=150°,则∠BCD的度数为
°.
19.如图,如果AB∥CD,则角α=130°,γ=20°,则β=
.
20.已知∠A与的∠B两边分别平行,且∠A比∠B的3倍少20°,则∠A的大小是
.
21.已知:在三角形ABC中,作AD⊥BC于点D,作DE∥AB交AC于点E,再在AB上取一点F,作∠BFG=∠ADE交BC于点G.
求证:FG⊥BC.
22.如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠ECG=90°﹣∠HAE.求证:BH∥CD.
23.如图,EF∥AD,∠1=∠2.
(1)若∠B=55°,求∠BDG的度数;
(2)若AD平分∠BAC,直接写出∠DGC与∠FEA的数量关系.
24.已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明:∠BFD=∠ABC;
(2)若∠ABC=40°,EG∥AD,EH⊥BE,求∠HEG的度数.
25.直线AB∥CD,E为直线AB、CD之间的一点,完成以下问题:
(1)如图1,若∠B=15°,∠BED=90°,则∠D=
;
(2)如图2,若∠B=α,∠D=β,求出∠BED的度数(用a、β表示);
(3)如图3,若∠B=α,∠C=β,则a、β与∠BEC之间有什么等量关系?请猜想证明.
26.直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点.
(1)若点P在直线CD上,如图①,∠α=50°,则∠2=
°.
(2)若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;
(3)若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由.
27.已知直线AB∥CD,M是直线AB上一点,N是直线CD上一点,点P在AB,CD之间.
(1)如图1,求证:∠BMP+∠DNP=∠MPN;
(2)如图2,NQ⊥CD,MQ⊥MP,若∠PND=30°,∠MPN=100°,直接写出∠MQN的度数.
28.如图,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG=90°,点F在直线AD上,∠AHG=90°.
(1)找出一个角与∠D相等,并说明理由;
(2)如果∠ECF=60°,求∠BCD的度数;
(3)在(2)的条件下,点C(点C不与点B、H重合)从点B出发,沿射线BG的方向运动,其他条件不变,请求出∠BAF的度数.
参考答案
1.解:依照题意画出图形,如图所示.
∵直线l1∥直线l2,
∴∠1+∠2=180°,
∴∠2=180°﹣∠1=180°﹣40°=140°,
∴∠3=∠2=140°,
∴第二次是右拐140°.
故选:D.
2.解:如图,过E作EG∥AB,EG交FC于点O,
∵AB∥CD,
∴AB∥CD∥EG,
∴∠A+∠AEG=180°,∠C=∠FOG,
∵∠FOG=∠F+∠FEG=∠F+∠FEA+∠AEG,
∴∠A+∠AEG=∠A+∠C﹣(∠F+∠FEA)=180°,
∴∠A+∠C﹣∠F﹣∠E=180°,
故选:C.
3.解:作直线l平行于直角三角板的斜边,
可得:∠2=∠3=45°,∠5=∠4=60°,
故∠1的度数是:45°+60°=105°.
故选:D.
4.解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°﹣116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2﹣∠1=116°﹣20°=96°,
∴∠ADC=180°﹣96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
5.解:延长直角三角板的一边交于直线b,给各角标上序号,则∠4=90°,如图所示,
∵直线a∥b,
∴∠3=∠1=130°.
又∵∠3=∠2+∠4,
即130°=∠2+90°,
∴∠2=130°﹣90°=40°.
故选:A.
6.解:过C点作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠α=∠BCF,∠β+∠DCF=180°,
∵BC⊥CD,
∴∠BCF+∠DCF=90°,
∴∠α+180°﹣∠β=90°,
∴∠β﹣∠α=90°,
∴β随α增大而增大,
故选:C.
7.解:如右图所示,
∵a∥b,
∴∠1=∠4,
∴∠1=70°,
∴∠4=70°,
∵∠3=50°,∠2+∠3+∠4=180°,
∴∠2=180°﹣∠3﹣∠4=180°﹣50°﹣70°=60°,
故选:C.
8.解:∵a∥b,c∥d,
∴∠2=∠3,∠1+∠2=180°,
∴∠1+∠3=180°,
∵∠3=∠4,∠2=∠5,
∴∠1+∠4=180°,∠1+∠5=180°,
故选:D.
9.解:∵直线a∥b,
∴∠1=∠CBA,
∵AC⊥AB,
∴∠2+∠CBA=90°,
∴∠2+∠1=90°,
∵∠2=52°,
∴∠1=38°,
故答案为:38°.
10.解:∵AB∥CD,∠1=130°,
∴∠CFB=∠1=130°,
∴∠BFD=180°﹣∠CFB=180°﹣130°=50°,
∵DG⊥BF,
∴∠DGF=90°,
∴∠2=90°﹣∠BFD=90°﹣50°=40°,
故答案为40°.
11.解:过点E作EM∥AB,过点F作FN∥AB,如图所示.
∵EM∥AB,AB∥CD,
∴EM∥CD,
∴∠AEM=∠EAB,∠CEM=∠ECD.
同理,可得:∠AFN=∠FAB,∠CFN=∠FCD.
又∵∠EAF=∠EAB,∠ECF=∠ECD,
∴∠EAB=∠FAB,∠ECD=∠FCD.
∴∠AEC=∠AEM+∠CEM=∠EAB+∠ECD=(∠FAB+∠FCD)=(∠AFN+∠CFN)=∠AFC=90°.
故答案为:90.
12.解:∵AE∥BD,
∴∠1=∠3=88°,
∵∠3=∠2+∠C,
∴∠C=∠3﹣∠2=88°﹣28°=60°,
故答案为:60°.
13.解:如图,∵AB∥CD,
∴∠5=180°﹣∠2,
∵AC∥BD,
∴∠3=∠5,
∵AE∥BF,
∴∠1=∠6,
∵EF∥AB,
∴∠4=∠6,
∴∠3﹣∠4=180°﹣∠2﹣∠1=180°﹣(∠1+∠2)=77°.
故答案为:77°.
14.解:∵AB∥CD,
∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,
∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠1+∠3=45°,
∵∠5=∠2+∠3,
∴∠5=∠1+∠3=45°,
即∠BFD=45°,
故答案为:45°.
15.解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
16.解:∵∠BOC=130°,
∴∠AOD=130°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠DOE=130°﹣90°=40°
故答案为:40°.
17.解:∵AB∥CD,∠C=25°,
∴∠ABE=∠C=25°,
又∵∠A=43°,
∴∠AEB=180°﹣∠A﹣∠ABE=180°﹣43°﹣25°=112°,
故答案为:112°.
18.解:过点C作CF∥AB,
∵AB∥DE,
∴AB∥DE∥CF,
∴∠ABC=∠BCF,∠CDE+∠DCF=180°,
∵∠ABC=76°,∠CDE=150°,
∴∠BCF=76°,∠DCF=30°,
∴∠BCD=46°,
故答案为:46.
19.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠D=∠FED,
∴∠AEF=180°﹣130°=50°,∠FED=20°,
∴∠AED=∠AEF+∠FED=50°+20°=70°.
即β=70°.
故答案为:70°.
20.解:因为∠A与的∠B两边分别平行,
所以∠A与∠B相等或互补,
因为∠A比∠B的3倍少20°,
所以∠A=3∠B﹣20°,
①当∠A=∠B时,
∠A=3∠A﹣20°,
解得∠A=10°;
②当∠A+∠B=180°时,
∠A=3(180°﹣∠A)﹣20°,
解得∠A=130°.
所以∠A的大小是10°或130°.
故答案为:10°或130°.
21.证明:∵AD⊥BC,
∴∠ADB=90°.
∵DE∥AB,
∴∠BAD=∠ADE,
∵∠BFG=∠ADE,
∴∠BAD=∠BFG,
∴AD∥FG,
∴∠FGB=∠ADB=90°,
∴FG⊥BC.
22.证明:过点E作EF∥BH,
∴∠HAE=∠AEF,
∵AE⊥CE,
∴∠AEC=90°
即∠AEF+∠CEF=90°,
∴∠HAE+∠CEF=90°,
∴∠CEF=90°﹣∠HAE,
∵∠ECG=90°﹣∠HAE,
∴∠CEF=∠ECG,
∴EF∥CD,
∵EF∥BH,
∴BH∥CD.
23.解:(1)∵EF∥AD,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥BA,
∴∠B+∠BDG=180°,
∵∠B=55°,
∴∠BDG=125°;
(2)∠DGC+∠FEA=180°,
理由:∵AD平分∠BAC,
∴∠BAC=2∠3,
由(1)知,DG∥BA,
∴∠CGD=∠BAC,
∴∠CGD=2∠3,
∵EF∥AD,
∴∠FEA+∠3=180°,
∴∠DGC+∠FEA=180°.
24.解:(1)∵∠BFD是△ABF的外角,
∴∠BFD=∠BAD+∠ABF,
∵∠BAD=∠EBC,
∴∠BAD+∠ABF=∠EBC+∠ABF,
即∠BFD=∠ABC;
(2)∵∠ABC=40°,∠BFD=∠ABC,
∴∠BFD=40°,
∵EG∥AD,
∴∠BFD=∠BEG,
∴∠BEG=40°,
∵EH⊥BE,
∴∠BEH=90°,
∴∠HEG=∠BEH﹣∠BEG=50°.
25.解:(1)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为:75°;
(2)过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°﹣α﹣β,
故答案为:∠BED=360°﹣α﹣β;
(3)猜想:∠BEC=180°﹣α+β.
证明:过点E作EF∥AB,
则∠BEF=180°﹣∠B=180°﹣α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°﹣α+β.
26.解:①∵AB∥CD,∠α=50°
∴∠2=∠α=50°,
故答案为50;
(2)∠α=∠1+∠2.
证明:过P作PG∥AB,
∵AB∥CD,
∴PG∥AB∥CD,
∴∠2=∠EPG,∠1=∠FPG,
∵∠α=∠EPF=∠EPG+∠FPG,
∴∠α=∠1+∠2;
(3)不成立.
理由:过P作PH∥AB,
∵AB∥CD,
∴PH∥AB∥CD,
∴∠2=∠EPH,∠1=∠FPH,
∵∠α=∠EPF=∠EPH﹣∠FPH,
∴∠α=∠2﹣∠1,
故不成立.
27.(1)证明:过P作PG∥AB,
∵AB∥CD,
∴AB∥CD∥PG,
∴∠BMP=∠MPG,∠GPN=∠PND,
∴∠BMP+∠PND=∠MPG+∠GPN,
∴∠MPN=∠BMP+∠PND;
(2)解:∵NQ⊥CD,MQ⊥MP,
∴∠QMP=∠QND=90°,
∵∠PND=30°,
∴∠QNP=90°﹣30°=60°,
∵∠MPN=100°,
∴∠MQN=360°﹣100°﹣60°﹣90°=110°.
28.解:(1)与∠D相等的角为∠DCG,∠ECF,∠B,
∵AD∥BC,
∴∠D=∠DCG,
∵∠FCG=90°,∠DCE=90°,
∴∠ECF=∠DCG,
∴∠D=∠ECF,
∵AB∥DC,
∴∠DCG=∠B,
∴∠B=∠D,
∴与∠D相等的角为∠DCG,∠ECF,∠B;
(2)∵∠ECF=60°,∠DCE=90°,
∴∠FCD=30°,
又∵∠BCF=90°,
∴∠BCD=30°+90°=120°;
(3)如图,当点C在线段BH上时,点F在DA延长线上,
∠ECF=∠DCG=∠B=60°,
∵AD∥BC,
∴∠BAF=∠B=60°;
如图,当点C在BH延长线上时,点F在线段AD上,
∵∠B=60°,AD∥BC,
∴∠BAF=180°﹣60°=120°.
综上所述,∠BAF的度数为60°或120°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
