2020-2021学年七年级数学北师大版下册第三章 变量之间的关系 单元同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册第三章 变量之间的关系 单元同步练习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 81.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 10:41:57 | ||
图片预览



文档简介
2020-2021学年北师大版七年级数学下册第三章
变量之间的关系
单元同步练习题
A组(基础题)
一、填空题
1.多边形内角和α与边数之间的关系是α=(n-2)180°,这个关系式中的变量是_______,常量(不变的量)是_______.
2.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.06毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,则y与x之间的函数关系式是_______.
3.亮亮骑自行车到距家9千米的体育馆看一场球赛,开始以正常速度匀速行驶,途中自行车出故障,他只好停下来修车.车修好后,他加速继续匀速赶往体育馆,其速度为原正常速度的倍,结果正好按预计时间(如果自行车不出故障,以正常速度匀速行驶到达体育馆的时间)到达.亮亮行驶的路程s(千米)与时间t(分钟)之间的关系如图所示,那么他修车占用的时间为_______分钟.
4.如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时,甲、乙两家售价一样;②买1件时,买乙家的合算;③买3件时,买甲家的合算;④买乙家的1件售价约为3元.其中正确的说法是_______.(填序号)
二、选择题
5.
已知甲、乙两地相距20
km,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(h)关于行驶速度v(km/h)的关系式是(
)
A.t=20v
B.t=
C.t=
D.t=
6.已知长方形的周长为24
cm,其中一边长为x
cm(其中x>0),面积为y
cm2,则这个长方形中y与x的关系可以写为(
)
A.y=x2
B.y=(12-x)2
C.y=2(12-x)
D.y=(12-x)x
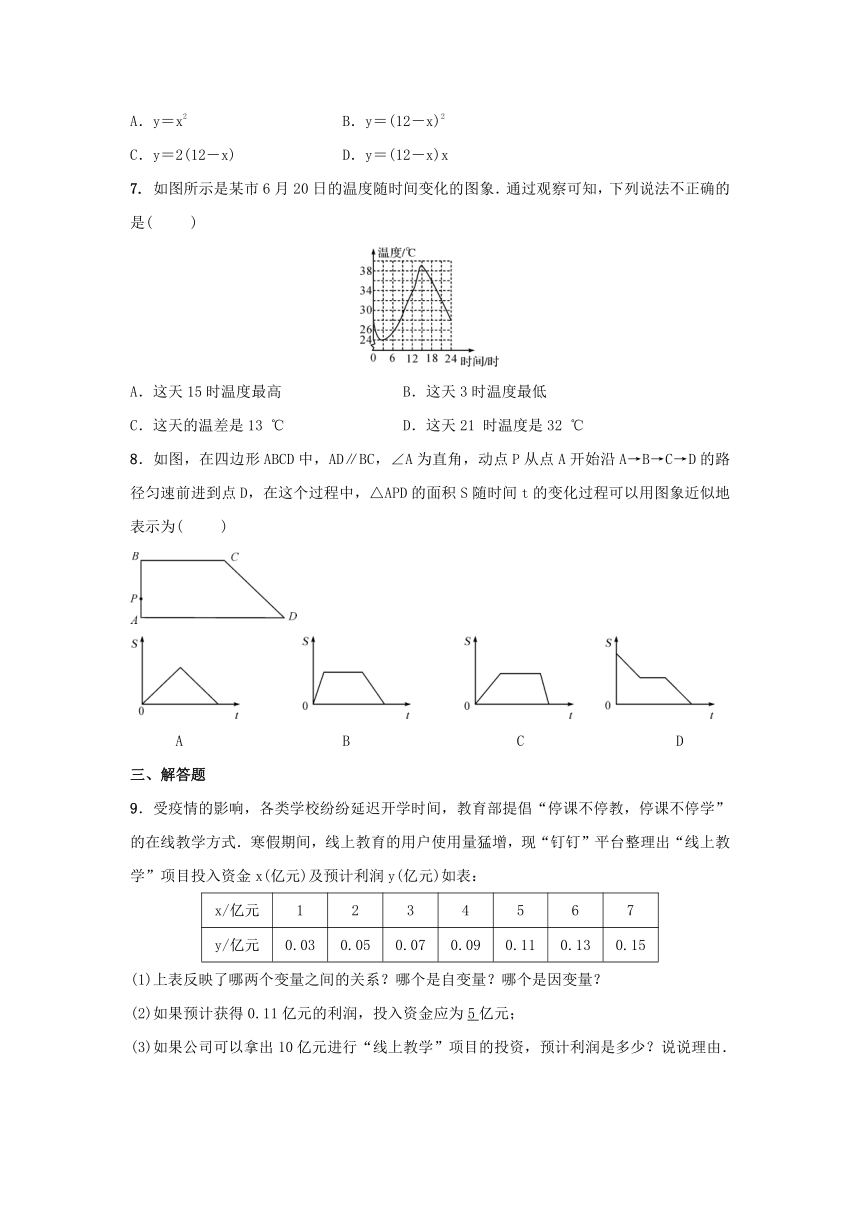
7.
如图所示是某市6月20日的温度随时间变化的图象.通过观察可知,下列说法不正确的是(
)
A.这天15时温度最高
B.这天3时温度最低
C.这天的温差是13
℃
D.这天21
时温度是32
℃
8.如图,在四边形ABCD中,AD∥BC,∠A为直角,动点P从点A开始沿A→B→C→D的路径匀速前进到点D,在这个过程中,△APD的面积S随时间t的变化过程可以用图象近似地表示为(
)
A
B
C
D
三、解答题
9.受疫情的影响,各类学校纷纷延迟开学时间,教育部提倡“停课不停教,停课不停学”的在线教学方式.寒假期间,线上教育的用户使用量猛增,现“钉钉”平台整理出“线上教学”项目投入资金x(亿元)及预计利润y(亿元)如表:
x/亿元
1
2
3
4
5
6
7
y/亿元
0.03
0.05
0.07
0.09
0.11
0.13
0.15
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计获得0.11亿元的利润,投入资金应为5亿元;
(3)如果公司可以拿出10亿元进行“线上教学”项目的投资,预计利润是多少?说说理由.
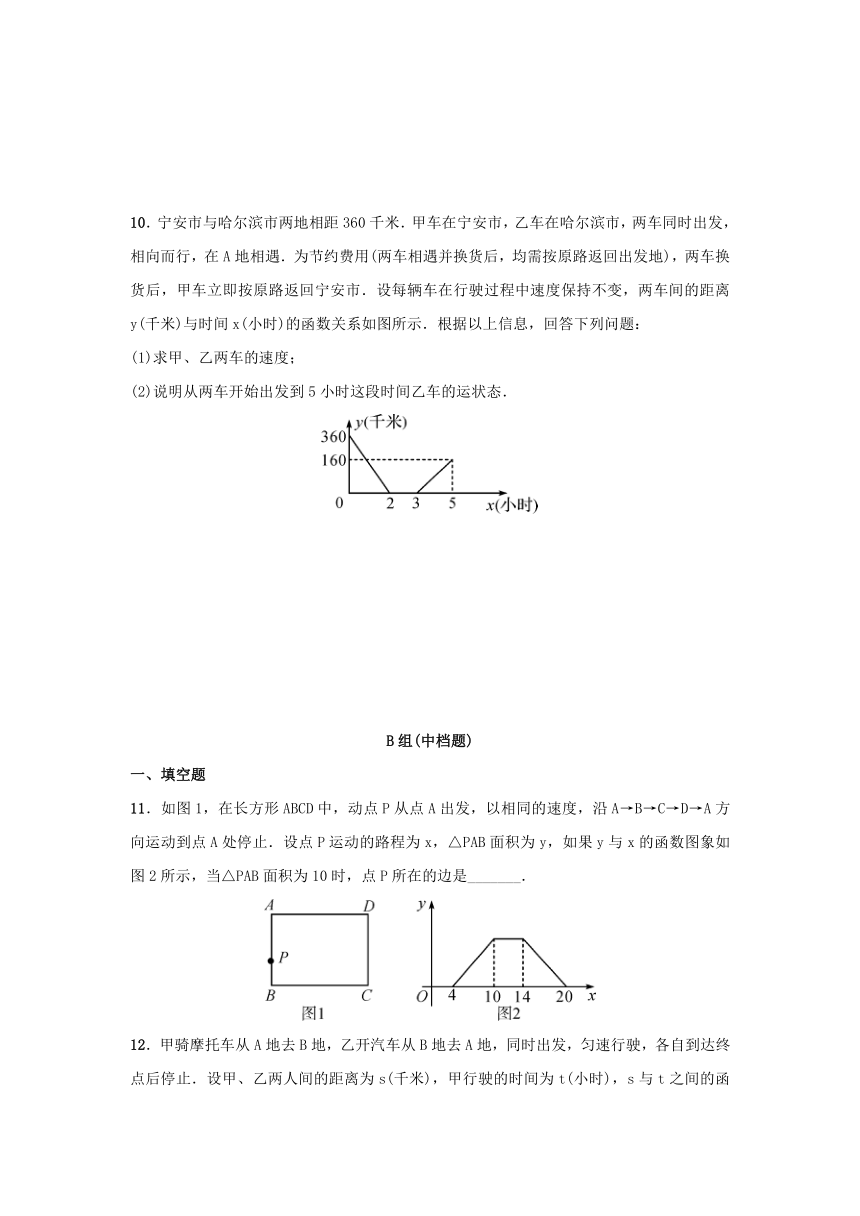
10.宁安市与哈尔滨市两地相距360千米.甲车在宁安市,乙车在哈尔滨市,两车同时出发,相向而行,在A地相遇.为节约费用(两车相遇并换货后,均需按原路返回出发地),两车换货后,甲车立即按原路返回宁安市.设每辆车在行驶过程中速度保持不变,两车间的距离y(千米)与时间x(小时)的函数关系如图所示.根据以上信息,回答下列问题:
(1)求甲、乙两车的速度;
(2)说明从两车开始出发到5小时这段时间乙车的运状态.
B组(中档题)
一、填空题
11.如图1,在长方形ABCD中,动点P从点A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,如果y与x的函数图象如图2所示,当△PAB面积为10时,点P所在的边是_______.
12.甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止.设甲、乙两人间的距离为s(千米),甲行驶的时间为t(小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数有_______个.
13.已知关系式f(x)=1+,其中f(a)表示x=a时关系式对应的值,如f(x)=1+,f(1)=1+,f(2)=1+,f(a)=1+,则f(1)·f(2)·f(3)·…·f(100)=_______.
二、解答题
14.
如图,自行车每节链条的长度为2.5
cm,交叉重叠部分的圆的直径为0.8
cm.
(1)观察图形,填写下表:
链条的节数/节
2
3
4
…
链条的长度/cm
4.2
5.9
7.6
…
(2)如果x节链条的长度为y(cm)
,那么y与x之间的关系式是什么?
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
C组(综合题)
15.如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设两点之间的距离为s(厘米),动点P的运动时间为t(秒),图2表示s与t之间的函数关系.
(1)求动点P,Q运动的速度;
(2)图2中,a=3,b=6,c=6;
(3)当a≤t≤c时,求s与t之间的函数关系式(即线段MN对应的函数关系式).
参考答案
2020-2021学年北师大版七年级数学下册第三章
变量之间的关系
单元同步练习题
A组(基础题)
一、填空题
1.多边形内角和α与边数之间的关系是α=(n-2)180°,这个关系式中的变量是n,α,常量(不变的量)是-2,180°.
2.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.06毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,则y与x之间的函数关系式是y=6x.
3.亮亮骑自行车到距家9千米的体育馆看一场球赛,开始以正常速度匀速行驶,途中自行车出故障,他只好停下来修车.车修好后,他加速继续匀速赶往体育馆,其速度为原正常速度的倍,结果正好按预计时间(如果自行车不出故障,以正常速度匀速行驶到达体育馆的时间)到达.亮亮行驶的路程s(千米)与时间t(分钟)之间的关系如图所示,那么他修车占用的时间为5分钟.
4.如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时,甲、乙两家售价一样;②买1件时,买乙家的合算;③买3件时,买甲家的合算;④买乙家的1件售价约为3元.其中正确的说法是①②③.(填序号)
二、选择题
5.
已知甲、乙两地相距20
km,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(h)关于行驶速度v(km/h)的关系式是(B)
A.t=20v
B.t=
C.t=
D.t=
6.已知长方形的周长为24
cm,其中一边长为x
cm(其中x>0),面积为y
cm2,则这个长方形中y与x的关系可以写为(D)
A.y=x2
B.y=(12-x)2
C.y=2(12-x)
D.y=(12-x)x
7.
如图所示是某市6月20日的温度随时间变化的图象.通过观察可知,下列说法不正确的是(C)
A.这天15时温度最高
B.这天3时温度最低
C.这天的温差是13
℃
D.这天21
时温度是32
℃
8.如图,在四边形ABCD中,AD∥BC,∠A为直角,动点P从点A开始沿A→B→C→D的路径匀速前进到点D,在这个过程中,△APD的面积S随时间t的变化过程可以用图象近似地表示为(B)
A
B
C
D
三、解答题
9.受疫情的影响,各类学校纷纷延迟开学时间,教育部提倡“停课不停教,停课不停学”的在线教学方式.寒假期间,线上教育的用户使用量猛增,现“钉钉”平台整理出“线上教学”项目投入资金x(亿元)及预计利润y(亿元)如表:
x/亿元
1
2
3
4
5
6
7
y/亿元
0.03
0.05
0.07
0.09
0.11
0.13
0.15
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计获得0.11亿元的利润,投入资金应为5亿元;
(3)如果公司可以拿出10亿元进行“线上教学”项目的投资,预计利润是多少?说说理由.
解:(1)反映了投入资金x和预计利润y之间的关系,投入资金是自变量,预计利润是因变量.
(3)从表格数据看,y与x之间的关系为y=0.02x+0.01.
当x=10时,y=0.2+0.01=0.21,
故预计利润是0.21亿元.
10.宁安市与哈尔滨市两地相距360千米.甲车在宁安市,乙车在哈尔滨市,两车同时出发,相向而行,在A地相遇.为节约费用(两车相遇并换货后,均需按原路返回出发地),两车换货后,甲车立即按原路返回宁安市.设每辆车在行驶过程中速度保持不变,两车间的距离y(千米)与时间x(小时)的函数关系如图所示.根据以上信息,回答下列问题:
(1)求甲、乙两车的速度;
(2)说明从两车开始出发到5小时这段时间乙车的运状态.
解:(1)由题意知,甲、乙两车的速度之和为=180(千米/时).=80(千米/时).
因为180>80,所以换货后只有甲车运动.
则甲车速度为80千米/时.
乙车的速度为180-80=100(千米/时).
(2)乙车以100千米/时的速度从哈尔滨市出发2个小时到达A地,又在A地停留3个小时.
B组(中档题)
一、填空题
11.如图1,在长方形ABCD中,动点P从点A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,如果y与x的函数图象如图2所示,当△PAB面积为10时,点P所在的边是AD或BC.
12.甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止.设甲、乙两人间的距离为s(千米),甲行驶的时间为t(小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数有3个.
13.已知关系式f(x)=1+,其中f(a)表示x=a时关系式对应的值,如f(x)=1+,f(1)=1+,f(2)=1+,f(a)=1+,则f(1)·f(2)·f(3)·…·f(100)=5_151.
二、解答题
14.
如图,自行车每节链条的长度为2.5
cm,交叉重叠部分的圆的直径为0.8
cm.
(1)观察图形,填写下表:
链条的节数/节
2
3
4
…
链条的长度/cm
4.2
5.9
7.6
…
(2)如果x节链条的长度为y(cm)
,那么y与x之间的关系式是什么?
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
解:(2)y=2.5+(2.5-0.8)(x-1),即y=1.7x+0.8.
(3)当x=60时,y=1.7×60+0.8=102.8.
因为安装好的链条首尾相连,所以102.8-0.8=102(cm).
故这辆自行车上的链条(安装后)总长度为102
cm.
C组(综合题)
15.如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设两点之间的距离为s(厘米),动点P的运动时间为t(秒),图2表示s与t之间的函数关系.
(1)求动点P,Q运动的速度;
(2)图2中,a=3,b=6,c=6;
(3)当a≤t≤c时,求s与t之间的函数关系式(即线段MN对应的函数关系式).
解:(1)设动点P运动的速度为x厘米/秒,则动点Q运动的速度为2x厘米/秒,根据题意,得
2(x+2x)=12,解得x=2.
故动点P,Q运动的速度分别是2厘米/秒、4厘米/秒.
(3)由(2)得,a=3,b=6,c=6.
当3≤t≤6时,点Q到达点A停止运动,点P继续以2厘米/秒的速度向点B运动,则PQ=PA.
所以s=2t(3≤t≤6).
变量之间的关系
单元同步练习题
A组(基础题)
一、填空题
1.多边形内角和α与边数之间的关系是α=(n-2)180°,这个关系式中的变量是_______,常量(不变的量)是_______.
2.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.06毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,则y与x之间的函数关系式是_______.
3.亮亮骑自行车到距家9千米的体育馆看一场球赛,开始以正常速度匀速行驶,途中自行车出故障,他只好停下来修车.车修好后,他加速继续匀速赶往体育馆,其速度为原正常速度的倍,结果正好按预计时间(如果自行车不出故障,以正常速度匀速行驶到达体育馆的时间)到达.亮亮行驶的路程s(千米)与时间t(分钟)之间的关系如图所示,那么他修车占用的时间为_______分钟.
4.如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时,甲、乙两家售价一样;②买1件时,买乙家的合算;③买3件时,买甲家的合算;④买乙家的1件售价约为3元.其中正确的说法是_______.(填序号)
二、选择题
5.
已知甲、乙两地相距20
km,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(h)关于行驶速度v(km/h)的关系式是(
)
A.t=20v
B.t=
C.t=
D.t=
6.已知长方形的周长为24
cm,其中一边长为x
cm(其中x>0),面积为y
cm2,则这个长方形中y与x的关系可以写为(
)
A.y=x2
B.y=(12-x)2
C.y=2(12-x)
D.y=(12-x)x
7.
如图所示是某市6月20日的温度随时间变化的图象.通过观察可知,下列说法不正确的是(
)
A.这天15时温度最高
B.这天3时温度最低
C.这天的温差是13
℃
D.这天21
时温度是32
℃
8.如图,在四边形ABCD中,AD∥BC,∠A为直角,动点P从点A开始沿A→B→C→D的路径匀速前进到点D,在这个过程中,△APD的面积S随时间t的变化过程可以用图象近似地表示为(
)
A
B
C
D
三、解答题
9.受疫情的影响,各类学校纷纷延迟开学时间,教育部提倡“停课不停教,停课不停学”的在线教学方式.寒假期间,线上教育的用户使用量猛增,现“钉钉”平台整理出“线上教学”项目投入资金x(亿元)及预计利润y(亿元)如表:
x/亿元
1
2
3
4
5
6
7
y/亿元
0.03
0.05
0.07
0.09
0.11
0.13
0.15
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计获得0.11亿元的利润,投入资金应为5亿元;
(3)如果公司可以拿出10亿元进行“线上教学”项目的投资,预计利润是多少?说说理由.
10.宁安市与哈尔滨市两地相距360千米.甲车在宁安市,乙车在哈尔滨市,两车同时出发,相向而行,在A地相遇.为节约费用(两车相遇并换货后,均需按原路返回出发地),两车换货后,甲车立即按原路返回宁安市.设每辆车在行驶过程中速度保持不变,两车间的距离y(千米)与时间x(小时)的函数关系如图所示.根据以上信息,回答下列问题:
(1)求甲、乙两车的速度;
(2)说明从两车开始出发到5小时这段时间乙车的运状态.
B组(中档题)
一、填空题
11.如图1,在长方形ABCD中,动点P从点A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,如果y与x的函数图象如图2所示,当△PAB面积为10时,点P所在的边是_______.
12.甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止.设甲、乙两人间的距离为s(千米),甲行驶的时间为t(小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数有_______个.
13.已知关系式f(x)=1+,其中f(a)表示x=a时关系式对应的值,如f(x)=1+,f(1)=1+,f(2)=1+,f(a)=1+,则f(1)·f(2)·f(3)·…·f(100)=_______.
二、解答题
14.
如图,自行车每节链条的长度为2.5
cm,交叉重叠部分的圆的直径为0.8
cm.
(1)观察图形,填写下表:
链条的节数/节
2
3
4
…
链条的长度/cm
4.2
5.9
7.6
…
(2)如果x节链条的长度为y(cm)
,那么y与x之间的关系式是什么?
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
C组(综合题)
15.如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设两点之间的距离为s(厘米),动点P的运动时间为t(秒),图2表示s与t之间的函数关系.
(1)求动点P,Q运动的速度;
(2)图2中,a=3,b=6,c=6;
(3)当a≤t≤c时,求s与t之间的函数关系式(即线段MN对应的函数关系式).
参考答案
2020-2021学年北师大版七年级数学下册第三章
变量之间的关系
单元同步练习题
A组(基础题)
一、填空题
1.多边形内角和α与边数之间的关系是α=(n-2)180°,这个关系式中的变量是n,α,常量(不变的量)是-2,180°.
2.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.06毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,则y与x之间的函数关系式是y=6x.
3.亮亮骑自行车到距家9千米的体育馆看一场球赛,开始以正常速度匀速行驶,途中自行车出故障,他只好停下来修车.车修好后,他加速继续匀速赶往体育馆,其速度为原正常速度的倍,结果正好按预计时间(如果自行车不出故障,以正常速度匀速行驶到达体育馆的时间)到达.亮亮行驶的路程s(千米)与时间t(分钟)之间的关系如图所示,那么他修车占用的时间为5分钟.
4.如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时,甲、乙两家售价一样;②买1件时,买乙家的合算;③买3件时,买甲家的合算;④买乙家的1件售价约为3元.其中正确的说法是①②③.(填序号)
二、选择题
5.
已知甲、乙两地相距20
km,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(h)关于行驶速度v(km/h)的关系式是(B)
A.t=20v
B.t=
C.t=
D.t=
6.已知长方形的周长为24
cm,其中一边长为x
cm(其中x>0),面积为y
cm2,则这个长方形中y与x的关系可以写为(D)
A.y=x2
B.y=(12-x)2
C.y=2(12-x)
D.y=(12-x)x
7.
如图所示是某市6月20日的温度随时间变化的图象.通过观察可知,下列说法不正确的是(C)
A.这天15时温度最高
B.这天3时温度最低
C.这天的温差是13
℃
D.这天21
时温度是32
℃
8.如图,在四边形ABCD中,AD∥BC,∠A为直角,动点P从点A开始沿A→B→C→D的路径匀速前进到点D,在这个过程中,△APD的面积S随时间t的变化过程可以用图象近似地表示为(B)
A
B
C
D
三、解答题
9.受疫情的影响,各类学校纷纷延迟开学时间,教育部提倡“停课不停教,停课不停学”的在线教学方式.寒假期间,线上教育的用户使用量猛增,现“钉钉”平台整理出“线上教学”项目投入资金x(亿元)及预计利润y(亿元)如表:
x/亿元
1
2
3
4
5
6
7
y/亿元
0.03
0.05
0.07
0.09
0.11
0.13
0.15
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计获得0.11亿元的利润,投入资金应为5亿元;
(3)如果公司可以拿出10亿元进行“线上教学”项目的投资,预计利润是多少?说说理由.
解:(1)反映了投入资金x和预计利润y之间的关系,投入资金是自变量,预计利润是因变量.
(3)从表格数据看,y与x之间的关系为y=0.02x+0.01.
当x=10时,y=0.2+0.01=0.21,
故预计利润是0.21亿元.
10.宁安市与哈尔滨市两地相距360千米.甲车在宁安市,乙车在哈尔滨市,两车同时出发,相向而行,在A地相遇.为节约费用(两车相遇并换货后,均需按原路返回出发地),两车换货后,甲车立即按原路返回宁安市.设每辆车在行驶过程中速度保持不变,两车间的距离y(千米)与时间x(小时)的函数关系如图所示.根据以上信息,回答下列问题:
(1)求甲、乙两车的速度;
(2)说明从两车开始出发到5小时这段时间乙车的运状态.
解:(1)由题意知,甲、乙两车的速度之和为=180(千米/时).=80(千米/时).
因为180>80,所以换货后只有甲车运动.
则甲车速度为80千米/时.
乙车的速度为180-80=100(千米/时).
(2)乙车以100千米/时的速度从哈尔滨市出发2个小时到达A地,又在A地停留3个小时.
B组(中档题)
一、填空题
11.如图1,在长方形ABCD中,动点P从点A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,如果y与x的函数图象如图2所示,当△PAB面积为10时,点P所在的边是AD或BC.
12.甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止.设甲、乙两人间的距离为s(千米),甲行驶的时间为t(小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数有3个.
13.已知关系式f(x)=1+,其中f(a)表示x=a时关系式对应的值,如f(x)=1+,f(1)=1+,f(2)=1+,f(a)=1+,则f(1)·f(2)·f(3)·…·f(100)=5_151.
二、解答题
14.
如图,自行车每节链条的长度为2.5
cm,交叉重叠部分的圆的直径为0.8
cm.
(1)观察图形,填写下表:
链条的节数/节
2
3
4
…
链条的长度/cm
4.2
5.9
7.6
…
(2)如果x节链条的长度为y(cm)
,那么y与x之间的关系式是什么?
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
解:(2)y=2.5+(2.5-0.8)(x-1),即y=1.7x+0.8.
(3)当x=60时,y=1.7×60+0.8=102.8.
因为安装好的链条首尾相连,所以102.8-0.8=102(cm).
故这辆自行车上的链条(安装后)总长度为102
cm.
C组(综合题)
15.如图1,线段AB=12厘米,动点P从点A出发向点B运动,动点Q从点B出发向点A运动,两点同时出发,到达各自的终点后停止运动.已知动点Q运动的速度是动点P运动的速度的2倍.设两点之间的距离为s(厘米),动点P的运动时间为t(秒),图2表示s与t之间的函数关系.
(1)求动点P,Q运动的速度;
(2)图2中,a=3,b=6,c=6;
(3)当a≤t≤c时,求s与t之间的函数关系式(即线段MN对应的函数关系式).
解:(1)设动点P运动的速度为x厘米/秒,则动点Q运动的速度为2x厘米/秒,根据题意,得
2(x+2x)=12,解得x=2.
故动点P,Q运动的速度分别是2厘米/秒、4厘米/秒.
(3)由(2)得,a=3,b=6,c=6.
当3≤t≤6时,点Q到达点A停止运动,点P继续以2厘米/秒的速度向点B运动,则PQ=PA.
所以s=2t(3≤t≤6).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
