2.1.1平面(新人教A版必修2)
文档属性
| 名称 | 2.1.1平面(新人教A版必修2) |  | |
| 格式 | rar | ||
| 文件大小 | 39.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-14 09:44:59 | ||
图片预览





文档简介
(共20张PPT)
2.1 空间点、直线、平面之间
的位置关系
2.1.1 平 面
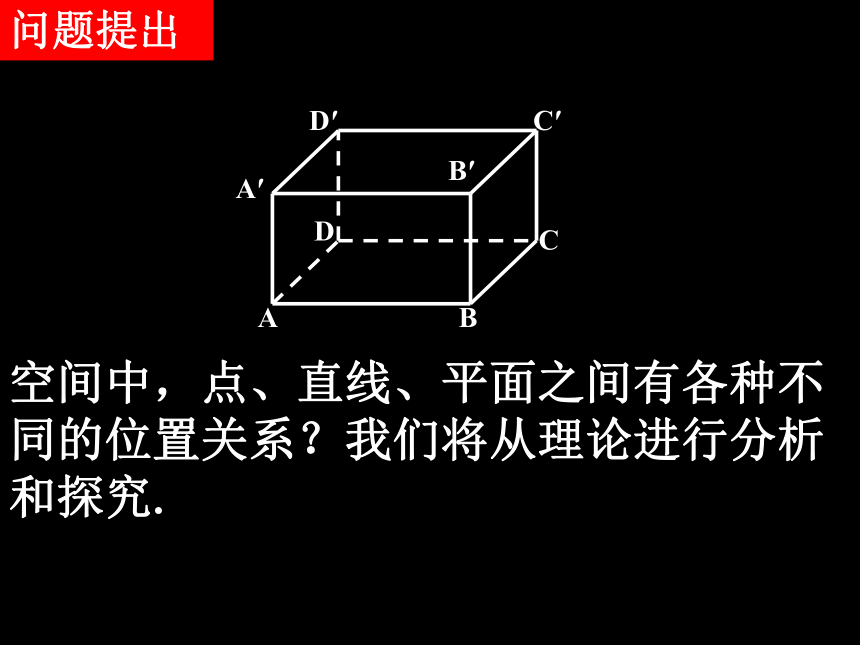
问题提出
A′
B′
C′
D′
A
B
C
D
空间中,点、直线、平面之间有各种不同的位置关系?我们将从理论进行分析和探究.
知识探究(一): 平面的概念、画法及表示
思考1:生活中有许多物体通常呈平 面形,你能列举一些实例吗?
思考3:直线是否有长短、粗细之分?
平面是否有大小、厚薄之别?
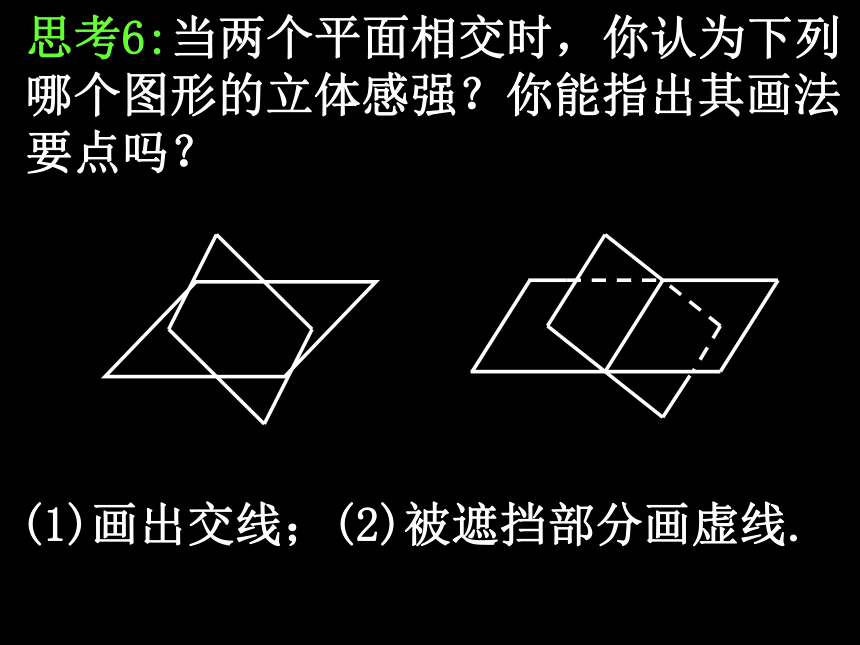
思考6:当两个平面相交时,你认为下列哪个图形的立体感强?你能指出其画法要点吗?
(1)画出交线;(2)被遮挡部分画虚线.
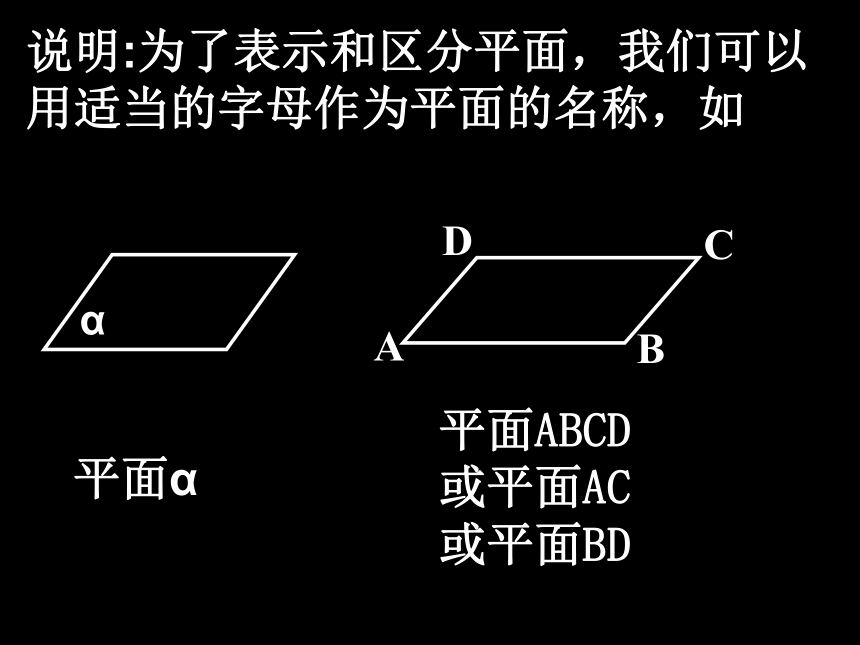
说明:为了表示和区分平面,我们可以用适当的字母作为平面的名称,如
平面α
α
A
B
C
D
平面ABCD或平面AC
或平面BD
“点P在直线l上”,
“点A在平面α内”,用集合符号可怎样表示?
“点P在直线l外”,
“点A在平面α外”用集合符号可怎样表示?
如果直线l上的所有点都在平面α内,就说直线l在平面α内,或者说平面α经过直线l,否则,就说直线l在平面α外.
那么“直线l在平面α内”,“直线l在平面α外”, 用集合符号可怎样表示?
知识探究(二):平面的基本性质1
思考1:如果直线l与平面α有一个公共点P,那么直线l是否在平面α内
思考2:如图,设直线l与平面α有一个公共点A,点B为直线l上另一个点,当点B逐渐与平面α靠近时,直线l上其余各点与平面α的位置关系如何变化?
.
A
A
B
α
思考3:如图,当点A、B落在平面α内时,直线l上其余各点与平面α的位置关系如何?由此可得什么结论?
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
思考4:公理1如何用符号语言表述?它有什么理论作用?
.
.
A
B
α
知识探究(三):平面的基本性质2
照相机,测量仪等器材的支架为何要做成三脚架?
思考3:经过任意三点都能确定一个平面吗?由此可得什么结论?
公理2 过不在一条直线上的三点,有且只有一个平面.
.
.
.
A
B
C
思考4:公理2可简述为“不共线的三点确定一个平面”, 它有什么理论作用?
知识探究(四):平面的基本性质3
思考1:如图,把三角板的一个角立在课桌面上,三角板所在的平面与桌面所在的平面是否只相交于一点B?为什么?
B
B
思考2:如果两条不重合
的直线有公共点,则其
公共点只有一个.如果两个不重合的平面有公共点,其公共点有多少个?这些公共点的位置关系如何?
思考3:根据上述分析可得什么结论?
P
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
你能说一说公理3有哪些理论作用吗?
确定两平面相交的依据,判断多点共线的依据.
公理3用符号语言可怎样表述
理论迁移
例1 如图,在正方体ABCD-A1B1C1D1中,
判断下列命题是否正确,并说明理由.
(1)直线AC1在平面A1B1C1D1内;
(2)设正方体上、下底面中心分别为 O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1;
(3)由点A,O,C可以确定一个平面;(4)平面AB1C1与平面AC1D重合.
B
B1
D1
A1
D
A
C
C1
O
O1
(1)直线AC1在平面A1B1C1D1内;
(2)设正方体上、下底面中心分别为 O、O1,则平面AA1C1C与平面BB1D1D 的交 线为OO1;
(3)由点A,O,C可以确定一个平面;(4)平面AB1C1与平面AC1D重合.
例2 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
A
B
β
α
a
l
(1)
a
b
P
l
β
α
(2)
作业:
P43练习:1,2, 3(做书上), 4.
P51习题2.1A组:1,2.
2.1 空间点、直线、平面之间
的位置关系
2.1.1 平 面
问题提出
A′
B′
C′
D′
A
B
C
D
空间中,点、直线、平面之间有各种不同的位置关系?我们将从理论进行分析和探究.
知识探究(一): 平面的概念、画法及表示
思考1:生活中有许多物体通常呈平 面形,你能列举一些实例吗?
思考3:直线是否有长短、粗细之分?
平面是否有大小、厚薄之别?
思考6:当两个平面相交时,你认为下列哪个图形的立体感强?你能指出其画法要点吗?
(1)画出交线;(2)被遮挡部分画虚线.
说明:为了表示和区分平面,我们可以用适当的字母作为平面的名称,如
平面α
α
A
B
C
D
平面ABCD或平面AC
或平面BD
“点P在直线l上”,
“点A在平面α内”,用集合符号可怎样表示?
“点P在直线l外”,
“点A在平面α外”用集合符号可怎样表示?
如果直线l上的所有点都在平面α内,就说直线l在平面α内,或者说平面α经过直线l,否则,就说直线l在平面α外.
那么“直线l在平面α内”,“直线l在平面α外”, 用集合符号可怎样表示?
知识探究(二):平面的基本性质1
思考1:如果直线l与平面α有一个公共点P,那么直线l是否在平面α内
思考2:如图,设直线l与平面α有一个公共点A,点B为直线l上另一个点,当点B逐渐与平面α靠近时,直线l上其余各点与平面α的位置关系如何变化?
.
A
A
B
α
思考3:如图,当点A、B落在平面α内时,直线l上其余各点与平面α的位置关系如何?由此可得什么结论?
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
思考4:公理1如何用符号语言表述?它有什么理论作用?
.
.
A
B
α
知识探究(三):平面的基本性质2
照相机,测量仪等器材的支架为何要做成三脚架?
思考3:经过任意三点都能确定一个平面吗?由此可得什么结论?
公理2 过不在一条直线上的三点,有且只有一个平面.
.
.
.
A
B
C
思考4:公理2可简述为“不共线的三点确定一个平面”, 它有什么理论作用?
知识探究(四):平面的基本性质3
思考1:如图,把三角板的一个角立在课桌面上,三角板所在的平面与桌面所在的平面是否只相交于一点B?为什么?
B
B
思考2:如果两条不重合
的直线有公共点,则其
公共点只有一个.如果两个不重合的平面有公共点,其公共点有多少个?这些公共点的位置关系如何?
思考3:根据上述分析可得什么结论?
P
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
你能说一说公理3有哪些理论作用吗?
确定两平面相交的依据,判断多点共线的依据.
公理3用符号语言可怎样表述
理论迁移
例1 如图,在正方体ABCD-A1B1C1D1中,
判断下列命题是否正确,并说明理由.
(1)直线AC1在平面A1B1C1D1内;
(2)设正方体上、下底面中心分别为 O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1;
(3)由点A,O,C可以确定一个平面;(4)平面AB1C1与平面AC1D重合.
B
B1
D1
A1
D
A
C
C1
O
O1
(1)直线AC1在平面A1B1C1D1内;
(2)设正方体上、下底面中心分别为 O、O1,则平面AA1C1C与平面BB1D1D 的交 线为OO1;
(3)由点A,O,C可以确定一个平面;(4)平面AB1C1与平面AC1D重合.
例2 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
A
B
β
α
a
l
(1)
a
b
P
l
β
α
(2)
作业:
P43练习:1,2, 3(做书上), 4.
P51习题2.1A组:1,2.
