3.1.1倾斜角与斜率(新人教A版必修2)
文档属性
| 名称 | 3.1.1倾斜角与斜率(新人教A版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 44.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-14 09:44:59 | ||
图片预览




文档简介
(共24张PPT)
3.1 直线的倾斜角与斜率
3.1.1 倾斜角与斜率
问题提出
1.在平面直角坐标系中,一次函数 y=kx+b的图象是什么?其中k,b的几何意义如何?
2.在平面直角坐标系中,经过一点P可以作无数条直线,如何区别这些直线的不同位置?
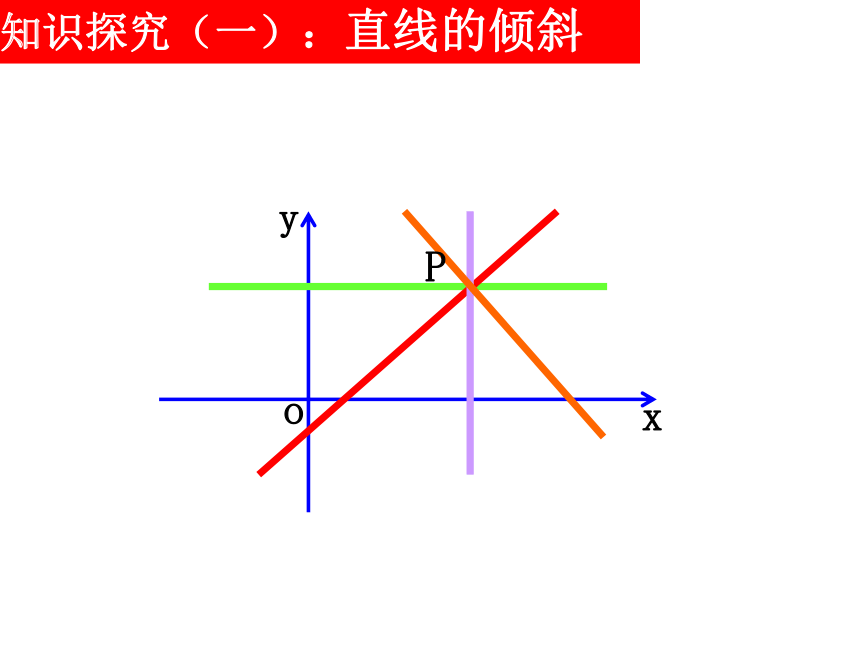
知识探究(一):直线的倾斜角
x
y
o
P
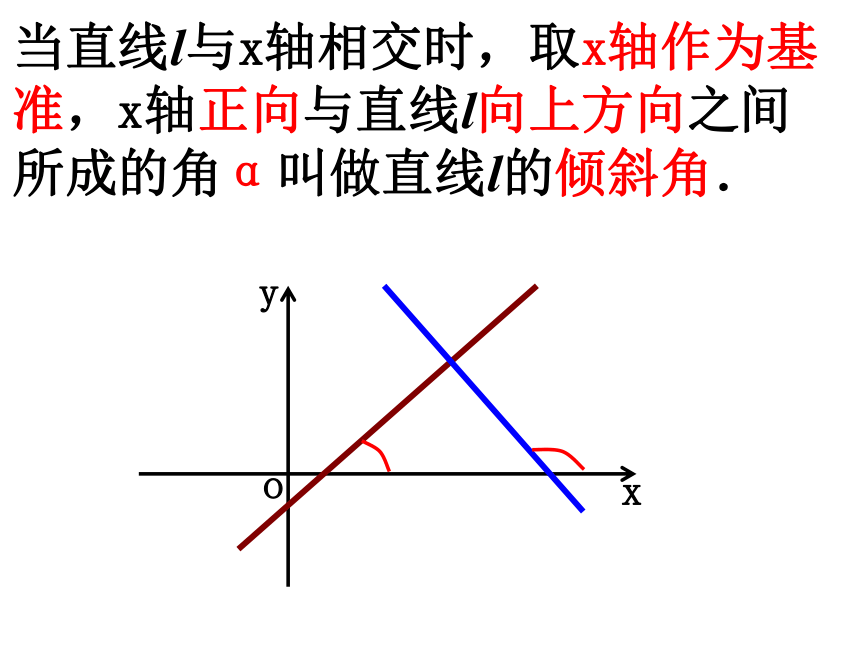
当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.
x
y
o
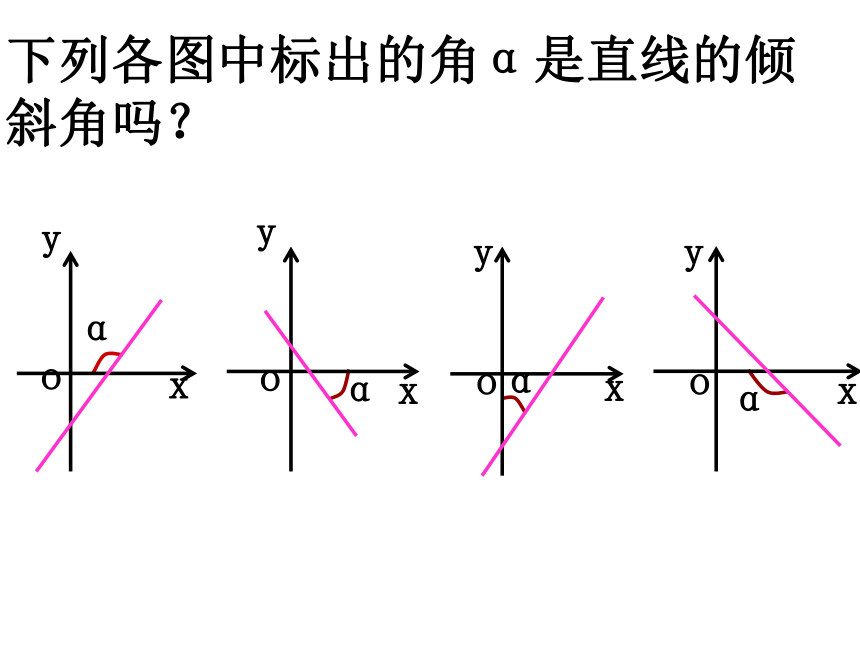
下列各图中标出的角α是直线的倾斜角吗?
x
o
y
α
x
o
y
α
x
o
y
α
o
α
x
y
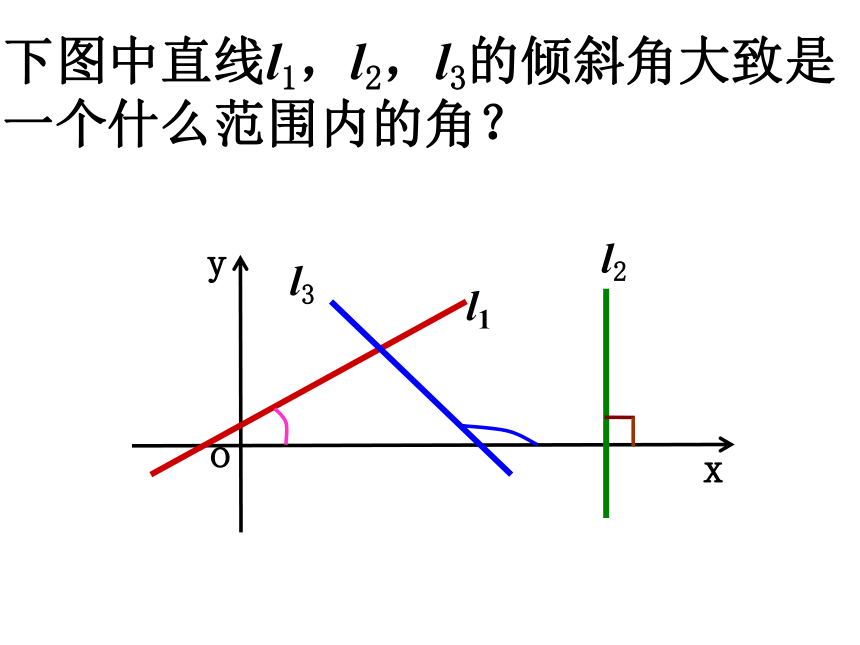
下图中直线l1,l2,l3的倾斜角大致是一个什么范围内的角?
x
y
o
l1
l2
l3
问: 任何一条直线都有倾斜角吗?
直线的倾斜角的取值范围
0°≤α<180°
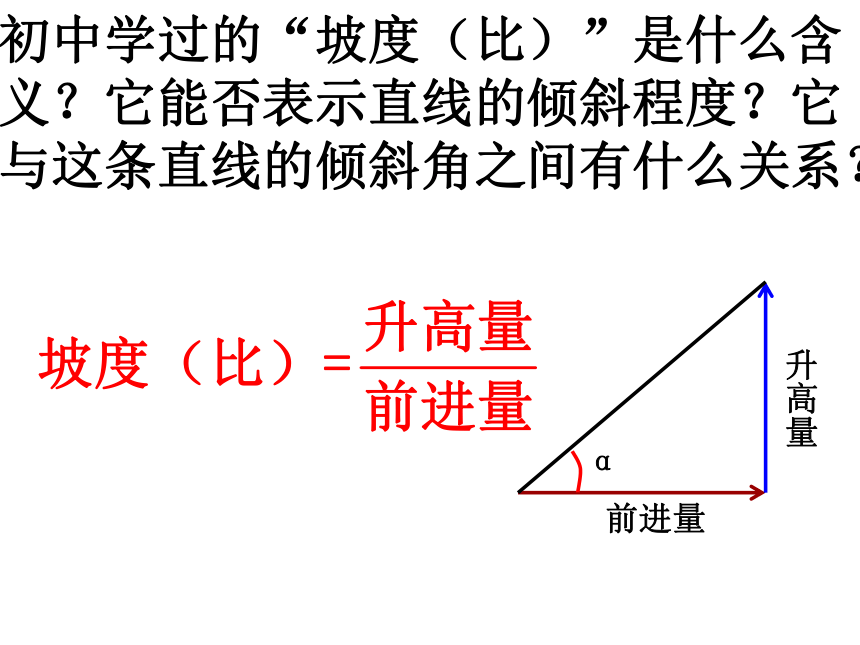
初中学过的“坡度(比)”是什么含义?它能否表示直线的倾斜程度?它与这条直线的倾斜角之间有什么关系?
前进量
升高量
α
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.常用小写字母k表示,即k=tanα,那么任何一条直线都有斜率吗?
倾斜角是900的直线(垂直与x轴的直线)没有斜率.
思考:当α是锐角时,有
tan(1800-α)=-tanα. 那么当倾斜角α=1200,1350,1500时,这条直线的斜率分别等于多少?
思考:当倾斜角α=00,300,450,600时,这条直线的斜率分别等于多少?
思考:斜率相等的直线其倾斜角相等吗?斜率大的直线其倾斜角也大吗?
问:倾斜角为锐角、钝角的直线的斜率的取值范围分别是什么?一般地,直线的斜率的取值范围是什么?
倾斜角为锐角时,k>0;倾斜角为钝角时,k<0;倾斜角为00时,k=0.
倾斜角是900没有斜率.
知识探究(三):直线的斜率公式
思考:在直角坐标系中,经过两点 A(2,4)、B(-1,3)的直线有几条?直线AB的斜率是多少?
α
x
y
o
A
B
C
α
(2,4)
(-1,3)
思考:一般地,已知直线上的两点P1(x1,y1),P2(x2,y2),且直线P1P2与x轴不垂直,即x1≠x2,直线P1P2的斜率是什么?
x
y
o
α
P1
P2
Q
α
x
y
o
α
P1
P2
Q
θ
(x1,y1)
思考:当直线P1P2平行于x轴或与x轴重合时,上述公式还适用吗?为什么?
思考:当直线P1P2平行于y轴或与y轴重合时,上述公式还适用吗?为什么?
思考:经过点A(a,b)、B(m,n)(a≠m)的直线的斜率是什么?
思考:对于三个不同的点A,B,C,若 ,则这三点的位置关系如何?
例1 如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是纯角。
O
x
y
A
C
B
例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
例题分析
O
x
y
A3
A1
A2
A4
直线的倾斜角与斜率
在平面直角坐标系中,当直线l与x轴相交时,我们取x轴作为基准, x轴正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角。
当直线l和x轴平行或重合时,我们规定直线的倾斜角为00.
倾斜角不是900的直线,它的倾斜角的正切叫做这条直线的斜率,常用k来表示.
k>0,则倾斜角是锐角;k<0,则倾斜角是钝角。
小结:
斜率公式
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
下列哪些说法是正确的( )
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是0或1800
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
练习
练习
l1
l2
l3
(3)如图,直线l1的倾斜角α1=300,
直线l1⊥l2,求l1、l2的斜率.
α1
α2
x
y
练习
作业:
P86练习:2,3,4.
P89习题3.1A组:3,4,5.
P90习题3.1B组:5,6.
3.1 直线的倾斜角与斜率
3.1.1 倾斜角与斜率
问题提出
1.在平面直角坐标系中,一次函数 y=kx+b的图象是什么?其中k,b的几何意义如何?
2.在平面直角坐标系中,经过一点P可以作无数条直线,如何区别这些直线的不同位置?
知识探究(一):直线的倾斜角
x
y
o
P
当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.
x
y
o
下列各图中标出的角α是直线的倾斜角吗?
x
o
y
α
x
o
y
α
x
o
y
α
o
α
x
y
下图中直线l1,l2,l3的倾斜角大致是一个什么范围内的角?
x
y
o
l1
l2
l3
问: 任何一条直线都有倾斜角吗?
直线的倾斜角的取值范围
0°≤α<180°
初中学过的“坡度(比)”是什么含义?它能否表示直线的倾斜程度?它与这条直线的倾斜角之间有什么关系?
前进量
升高量
α
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.常用小写字母k表示,即k=tanα,那么任何一条直线都有斜率吗?
倾斜角是900的直线(垂直与x轴的直线)没有斜率.
思考:当α是锐角时,有
tan(1800-α)=-tanα. 那么当倾斜角α=1200,1350,1500时,这条直线的斜率分别等于多少?
思考:当倾斜角α=00,300,450,600时,这条直线的斜率分别等于多少?
思考:斜率相等的直线其倾斜角相等吗?斜率大的直线其倾斜角也大吗?
问:倾斜角为锐角、钝角的直线的斜率的取值范围分别是什么?一般地,直线的斜率的取值范围是什么?
倾斜角为锐角时,k>0;倾斜角为钝角时,k<0;倾斜角为00时,k=0.
倾斜角是900没有斜率.
知识探究(三):直线的斜率公式
思考:在直角坐标系中,经过两点 A(2,4)、B(-1,3)的直线有几条?直线AB的斜率是多少?
α
x
y
o
A
B
C
α
(2,4)
(-1,3)
思考:一般地,已知直线上的两点P1(x1,y1),P2(x2,y2),且直线P1P2与x轴不垂直,即x1≠x2,直线P1P2的斜率是什么?
x
y
o
α
P1
P2
Q
α
x
y
o
α
P1
P2
Q
θ
(x1,y1)
思考:当直线P1P2平行于x轴或与x轴重合时,上述公式还适用吗?为什么?
思考:当直线P1P2平行于y轴或与y轴重合时,上述公式还适用吗?为什么?
思考:经过点A(a,b)、B(m,n)(a≠m)的直线的斜率是什么?
思考:对于三个不同的点A,B,C,若 ,则这三点的位置关系如何?
例1 如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是纯角。
O
x
y
A
C
B
例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
例题分析
O
x
y
A3
A1
A2
A4
直线的倾斜角与斜率
在平面直角坐标系中,当直线l与x轴相交时,我们取x轴作为基准, x轴正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角。
当直线l和x轴平行或重合时,我们规定直线的倾斜角为00.
倾斜角不是900的直线,它的倾斜角的正切叫做这条直线的斜率,常用k来表示.
k>0,则倾斜角是锐角;k<0,则倾斜角是钝角。
小结:
斜率公式
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
下列哪些说法是正确的( )
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是0或1800
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
练习
练习
l1
l2
l3
(3)如图,直线l1的倾斜角α1=300,
直线l1⊥l2,求l1、l2的斜率.
α1
α2
x
y
练习
作业:
P86练习:2,3,4.
P89习题3.1A组:3,4,5.
P90习题3.1B组:5,6.
