3.2.2直线的两点式方程(2)(新人教A版必修2)
文档属性
| 名称 | 3.2.2直线的两点式方程(2)(新人教A版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 384.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-14 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
复习回顾
点斜式
y-y1 = k(x-x1)
斜截式
y = kx + b
解:当 =2时,过点(2, 1)和(2,2)的直线斜率不存在,故其直线方程是x=2;
当 ≠2时。直线的斜率k=
因为直线过(2,1)点, 所以由直线方程的点斜式可得 ,即
综上所述,所求直线得方程为
练习:
求过点(2,1)和点( 2)的直线方程
例题分析
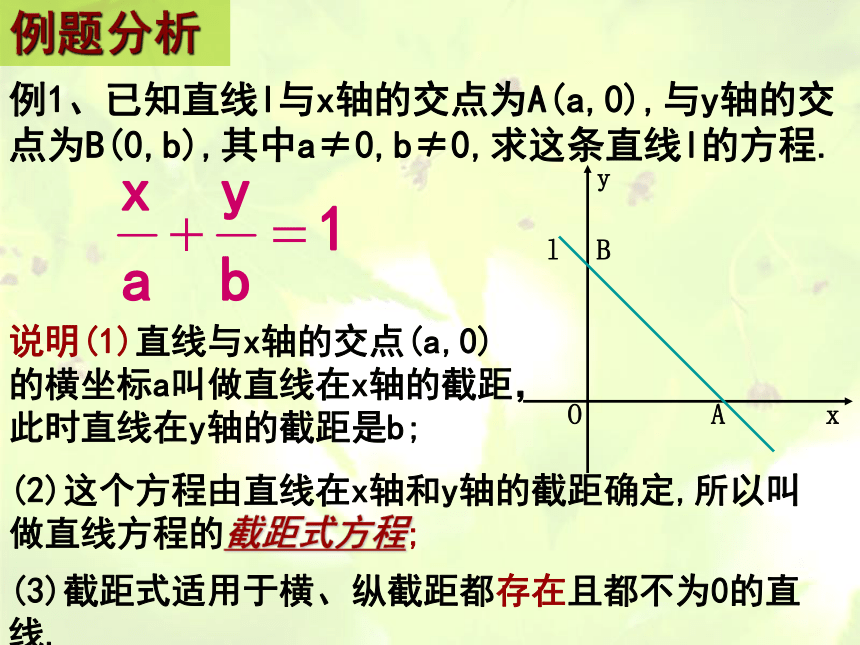
例1、已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求这条直线l的方程.
说明(1)直线与x轴的交点(a,0)的横坐标a叫做直线在x轴的截距,此时直线在y轴的截距是b;
x
l
B
A
O
y
(3)截距式适用于横、纵截距都存在且都不为0的直线.
(2)这个方程由直线在x轴和y轴的截距确定,所以叫做直线方程的截距式方程;
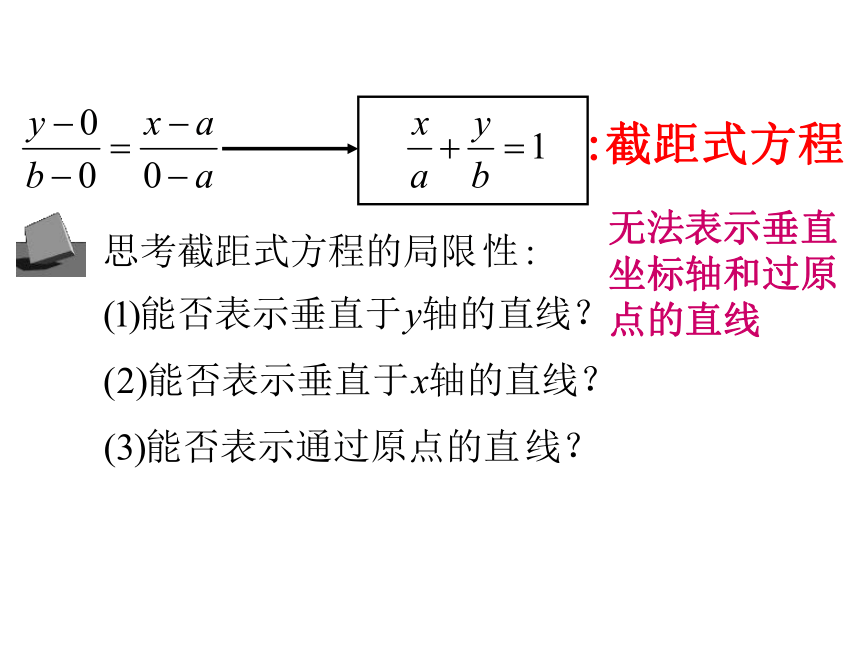
无法表示垂直坐标轴和过原点的直线
练习
B
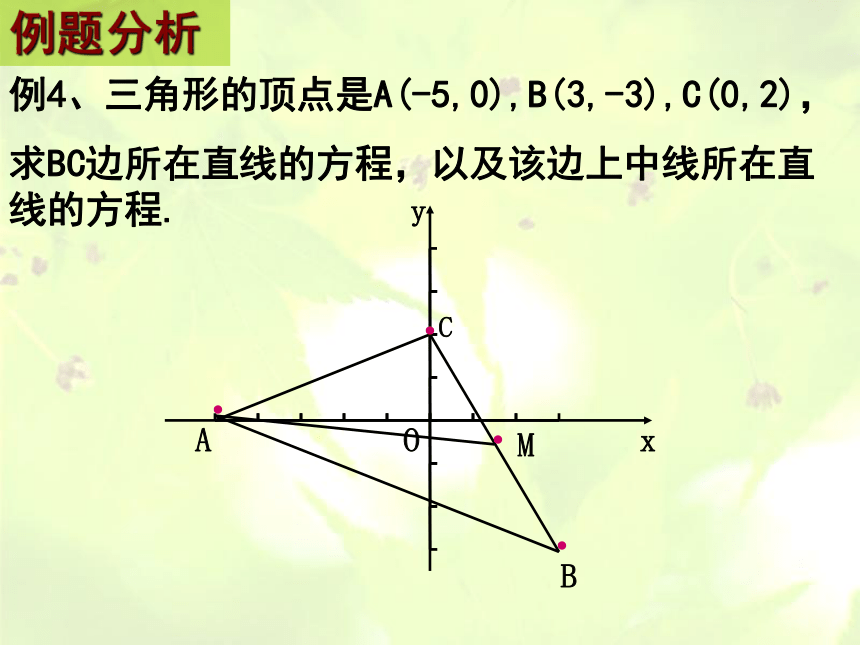
例4、三角形的顶点是A(-5,0),B(3,-3),C(0,2),
求BC边所在直线的方程,以及该边上中线所在直线的方程.
x
y
O
.
M
例题分析
B
.
A
.
.
C
P97 练习2,
练习
根据下列条件,求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2;
例2 求经过点P(2,3),且在两坐标轴上的截距相等的直线方程.
P100 习题8, 11
直线名称 已知条件 直线方程 使用范围
k
y
x
P
),
,
(
1
1
1
直线方程有哪几种形式?
点斜式
斜截式
两点式
截距式
问题1:平面内的任一条直线,一定可以用以上 四种形式之一表示吗?
直线方程的四种特殊形式各自都有自己的优点,但都有局限性,即都无法表示平面内的任一条直线
问题2:是否存在某种形式的直线方程,
它能表示平面内的任何一条直线?
上述四种直线方程,能否写成如下统一形式?
x+ y+ =0
上述四式都可以写成以下形式:
Ax+By+C=0, (A、B不同时为0)
①在直角坐标系中,任何一条直线的方程都是关于x,y的一 次方程吗
⑴直线和Y轴相交时:此时倾α≠90 0,
直线的斜率k存在,直线可表示成y=kx+b
⑵直线和Y轴平行(包括重合)时:此时倾斜角α=90 0,直线的斜率k不存在,不能用y =kx+b表示,这时方程可表示成x=xo
结论:任何一条直线的方程都是关于x,y的二元一次方程。
②任何关于x,y的二元一次方Ax+By+C=0(A,B不同时为零) 都表示直线吗
⑴B≠0时,方程化成 这是直线的斜截 式,
它表示为斜率为 – A/B,纵截距为- C/B的直线。
⑵B=0时,由于A,B不同时为零所以A≠0,此时,Ax+By+
C=0可化为x= -C / A,它表示为与Y轴平行(当C=0时)或重合
(当C=0时)的直线。
直线与二元一次方程的关系:
结论:(1)直线方程都是关于x,y的二元一次方程
(2)关于x,y的二元一次方程总表示一条直线。
我们把关于x,y的二元一次方程
(其中A、B不全为0)的形式,叫做直线的一般式方程,简称一般式.
已知两点A(-3,4),B(3, 2),过点P(2,-1)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围
练习
复习回顾
点斜式
y-y1 = k(x-x1)
斜截式
y = kx + b
解:当 =2时,过点(2, 1)和(2,2)的直线斜率不存在,故其直线方程是x=2;
当 ≠2时。直线的斜率k=
因为直线过(2,1)点, 所以由直线方程的点斜式可得 ,即
综上所述,所求直线得方程为
练习:
求过点(2,1)和点( 2)的直线方程
例题分析
例1、已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求这条直线l的方程.
说明(1)直线与x轴的交点(a,0)的横坐标a叫做直线在x轴的截距,此时直线在y轴的截距是b;
x
l
B
A
O
y
(3)截距式适用于横、纵截距都存在且都不为0的直线.
(2)这个方程由直线在x轴和y轴的截距确定,所以叫做直线方程的截距式方程;
无法表示垂直坐标轴和过原点的直线
练习
B
例4、三角形的顶点是A(-5,0),B(3,-3),C(0,2),
求BC边所在直线的方程,以及该边上中线所在直线的方程.
x
y
O
.
M
例题分析
B
.
A
.
.
C
P97 练习2,
练习
根据下列条件,求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2;
例2 求经过点P(2,3),且在两坐标轴上的截距相等的直线方程.
P100 习题8, 11
直线名称 已知条件 直线方程 使用范围
k
y
x
P
),
,
(
1
1
1
直线方程有哪几种形式?
点斜式
斜截式
两点式
截距式
问题1:平面内的任一条直线,一定可以用以上 四种形式之一表示吗?
直线方程的四种特殊形式各自都有自己的优点,但都有局限性,即都无法表示平面内的任一条直线
问题2:是否存在某种形式的直线方程,
它能表示平面内的任何一条直线?
上述四种直线方程,能否写成如下统一形式?
x+ y+ =0
上述四式都可以写成以下形式:
Ax+By+C=0, (A、B不同时为0)
①在直角坐标系中,任何一条直线的方程都是关于x,y的一 次方程吗
⑴直线和Y轴相交时:此时倾α≠90 0,
直线的斜率k存在,直线可表示成y=kx+b
⑵直线和Y轴平行(包括重合)时:此时倾斜角α=90 0,直线的斜率k不存在,不能用y =kx+b表示,这时方程可表示成x=xo
结论:任何一条直线的方程都是关于x,y的二元一次方程。
②任何关于x,y的二元一次方Ax+By+C=0(A,B不同时为零) 都表示直线吗
⑴B≠0时,方程化成 这是直线的斜截 式,
它表示为斜率为 – A/B,纵截距为- C/B的直线。
⑵B=0时,由于A,B不同时为零所以A≠0,此时,Ax+By+
C=0可化为x= -C / A,它表示为与Y轴平行(当C=0时)或重合
(当C=0时)的直线。
直线与二元一次方程的关系:
结论:(1)直线方程都是关于x,y的二元一次方程
(2)关于x,y的二元一次方程总表示一条直线。
我们把关于x,y的二元一次方程
(其中A、B不全为0)的形式,叫做直线的一般式方程,简称一般式.
已知两点A(-3,4),B(3, 2),过点P(2,-1)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围
练习
