3.3.2两点间的距离(新人教A版必修2)
文档属性
| 名称 | 3.3.2两点间的距离(新人教A版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 87.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-14 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
利用二元一次方程组的解讨论平面上两条直线的位置关系
已知方程组
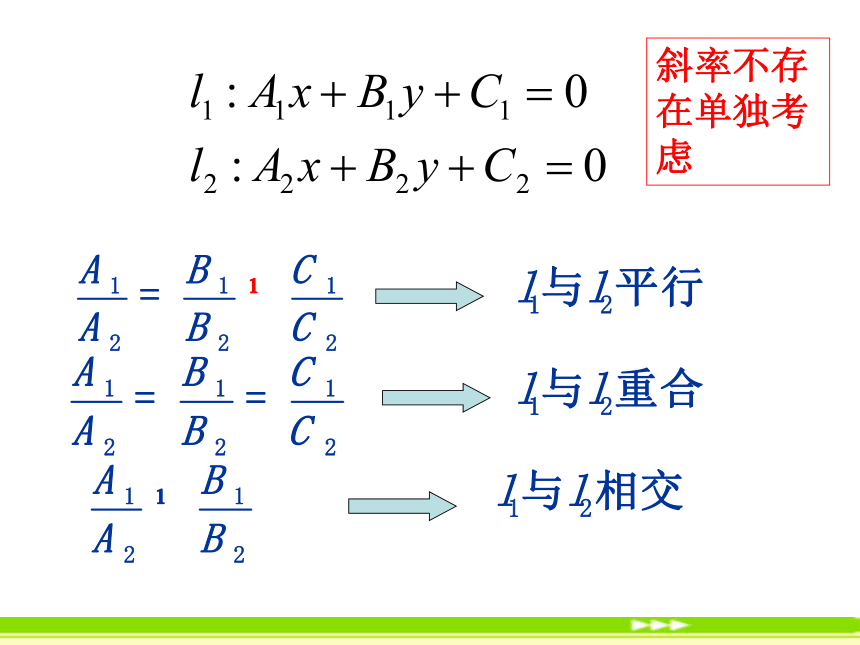
A1x+B1y+C1=0 (1)
A2x+B2y+C2=0 (2)
当A1,A2,B1,B2全不为零时
(1)×B2-(2)×B1得(A1B2-A2B1)x=B1C2-B2C1
讨论:⒈当A1B2-A2B1≠0时,方程组有唯一解
x = ——————
B1C2-B2C1
A1B2-A2B1
y= ——————
A1B2-A2B1
C1A2-C2A1
⒉当A1B2-A2B1=0, B1C2-B2C1≠0 时,方程组无解
⒊当A1B2-A2B1=0, B1C2-B2C1=0 时,方程组有无
穷多解。
斜率不存在单独考虑
判断下列各对直线的位置关系
(1)l1:2x-3y=7, l2:4x+2y=1;
(2)l1:2x-6y+4=0, l2:y=
(3)l1: l2:
练习
1、A和C取什么值时,直线Ax-2y-1=0与直线6x-
4y+C=0:
①平行,②相交,③ 重合,④ 垂直
例1
直线l1:x+ay-2a-2=0和l2:ax+y-1-a=0,
(1)若l1//l2,求a的值.
(2)若l1⊥l2,求a的值.
例2
a为何值时, 直线l1.(a-1)x-2y+4=0 l2:x-ay-1=0,(1)平行 (2)垂直
§3.3.4 两点间的距离
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 P2的距离| P1 P2 |呢
两点间的距离
y
x
o
P1
P2
y
x
o
P2
P1
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 P2的距离| P1 P2 |呢
两点间的距离
Q
(x2,y1)
y
x
o
P1
P2
(x1,y1)
(x2,y2)
练习
1、求下列两点间的距离:
(1)、A(6,0),B(-2,0) (2)、C(0,-4),D(0,-1)
(3)、P(6,0),Q(0,-2) (4)、M(2,1),N(5,-1)
例题分析
解:设所求点为P(x,0),于是有
解得x=1,所以所求点P(1,0)
求在x轴上与点A(5,12)的距离为13的坐标;
练习
例题分析
例4、证明平行四边形四条边的平方和等于两条对角线的平方和。
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
解:如图,以顶点A为坐标原点,AB所在直线为x轴,建立直角坐标系,则有A(0,0)
设B(a,0),D(b,c),由平行四边形的性质可得C(a+b,c)
因此,平行四边形四条边的平方和等于两条对角线的 平方和
A
B
D
C
用“坐标法”解决有关几何问题的基本步骤:
第一步;建立坐标系,
用坐标系表示有关的量
第二步:进行
有关代数运算
第三步:把代数运算结果
“翻译”成几何关系
练习
4、证明直角三角形斜边的中点到三个顶点的距离相等。
y
x
o
B
C
A
M
(0,0)
(a,0)
(0,b)
平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是
小结
利用二元一次方程组的解讨论平面上两条直线的位置关系
已知方程组
A1x+B1y+C1=0 (1)
A2x+B2y+C2=0 (2)
当A1,A2,B1,B2全不为零时
(1)×B2-(2)×B1得(A1B2-A2B1)x=B1C2-B2C1
讨论:⒈当A1B2-A2B1≠0时,方程组有唯一解
x = ——————
B1C2-B2C1
A1B2-A2B1
y= ——————
A1B2-A2B1
C1A2-C2A1
⒉当A1B2-A2B1=0, B1C2-B2C1≠0 时,方程组无解
⒊当A1B2-A2B1=0, B1C2-B2C1=0 时,方程组有无
穷多解。
斜率不存在单独考虑
判断下列各对直线的位置关系
(1)l1:2x-3y=7, l2:4x+2y=1;
(2)l1:2x-6y+4=0, l2:y=
(3)l1: l2:
练习
1、A和C取什么值时,直线Ax-2y-1=0与直线6x-
4y+C=0:
①平行,②相交,③ 重合,④ 垂直
例1
直线l1:x+ay-2a-2=0和l2:ax+y-1-a=0,
(1)若l1//l2,求a的值.
(2)若l1⊥l2,求a的值.
例2
a为何值时, 直线l1.(a-1)x-2y+4=0 l2:x-ay-1=0,(1)平行 (2)垂直
§3.3.4 两点间的距离
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 P2的距离| P1 P2 |呢
两点间的距离
y
x
o
P1
P2
y
x
o
P2
P1
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 P2的距离| P1 P2 |呢
两点间的距离
Q
(x2,y1)
y
x
o
P1
P2
(x1,y1)
(x2,y2)
练习
1、求下列两点间的距离:
(1)、A(6,0),B(-2,0) (2)、C(0,-4),D(0,-1)
(3)、P(6,0),Q(0,-2) (4)、M(2,1),N(5,-1)
例题分析
解:设所求点为P(x,0),于是有
解得x=1,所以所求点P(1,0)
求在x轴上与点A(5,12)的距离为13的坐标;
练习
例题分析
例4、证明平行四边形四条边的平方和等于两条对角线的平方和。
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
解:如图,以顶点A为坐标原点,AB所在直线为x轴,建立直角坐标系,则有A(0,0)
设B(a,0),D(b,c),由平行四边形的性质可得C(a+b,c)
因此,平行四边形四条边的平方和等于两条对角线的 平方和
A
B
D
C
用“坐标法”解决有关几何问题的基本步骤:
第一步;建立坐标系,
用坐标系表示有关的量
第二步:进行
有关代数运算
第三步:把代数运算结果
“翻译”成几何关系
练习
4、证明直角三角形斜边的中点到三个顶点的距离相等。
y
x
o
B
C
A
M
(0,0)
(a,0)
(0,b)
平面内两点P1(x1,y1), P2(x2,y2) 的距离公式是
小结
