4.1.1圆的标准方程 (新人教A版必修2)
文档属性
| 名称 | 4.1.1圆的标准方程 (新人教A版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 105.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-14 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
§4.1.1 圆的标准方程
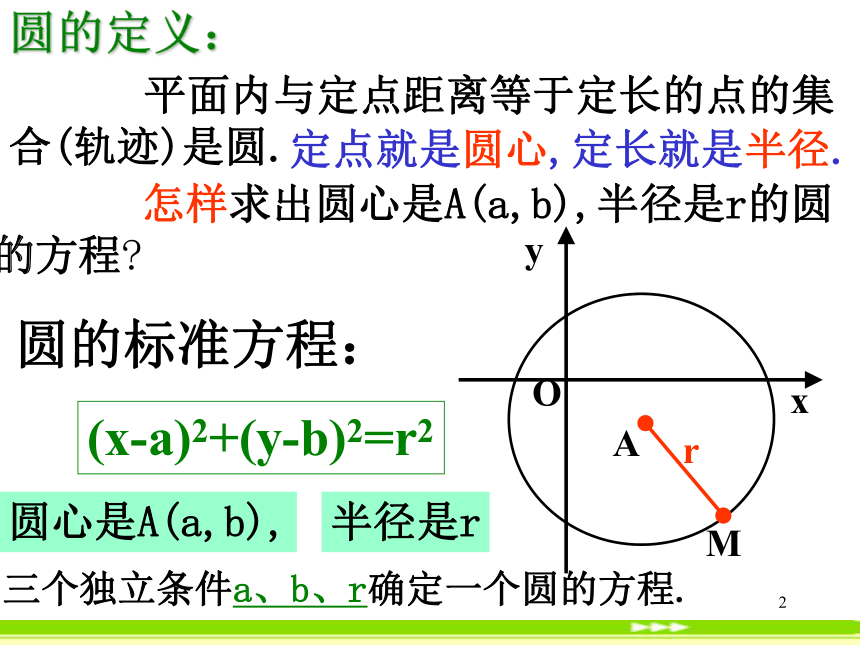
圆的定义:
怎样求出圆心是A(a,b),半径是r的圆的方程
平面内与定点距离等于定长的点的集合(轨迹)是圆.
(x-a)2+(y-b)2=r2
三个独立条件a、b、r确定一个圆的方程.
x
y
O
A
M
r
圆的标准方程:
定点就是圆心,
定长就是半径.
圆心是A(a,b),
半径是r
点M0(x0,y0)在圆(x-a)2+(y-b)2=r2上、内、外的条件是什么?
点M0在圆上
点M0在圆内
(x0-a)2+(y0-b)2=r2
(x0-a)2+(y0-b)2(x0-a)2+(y0-b)2>r2
点M0在圆外
例题分析
例1、写出圆心为A(2,-3),半径长等于5的圆的方程,并判断M1(5,-7),M2(4,-5), M3(6,-8)是在圆上或圆内或圆外?
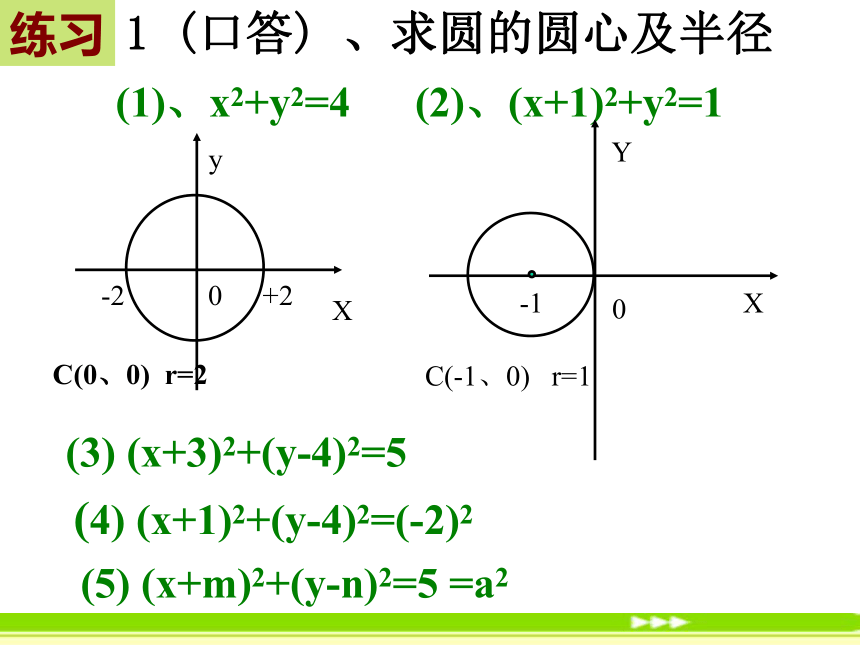
1 (口答) 、求圆的圆心及半径
(1)、x2+y2=4 (2)、(x+1)2+y2=1
练习
X
y
0
+2
-2
C(0、0) r=2
X
Y
0
-1
C(-1、0) r=1
(3) (x+3)2+(y-4)2=5
(5) (x+m)2+(y-n)2=5 =a2
(4) (x+1)2+(y-4)2=(-2)2
(1) x2+y2=9
(2) (x+3)2+(y-4)2=5
练习
2、写出下列圆的方程
3、圆心在(-1、2),与y轴相切的圆
(1)圆心在原点,半径是3
(2)圆心为(-3,4),半径为
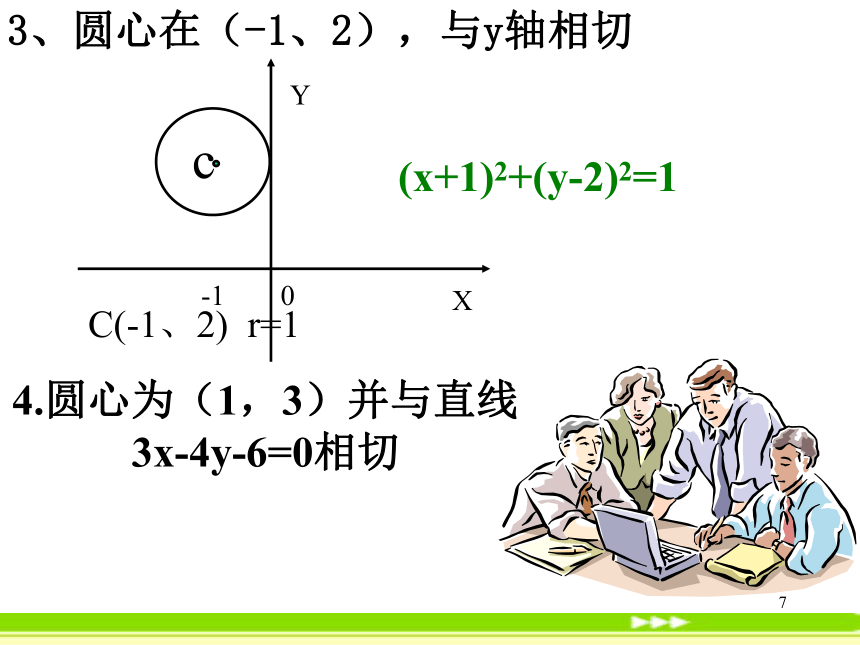
3、圆心在(-1、2),与y轴相切
X
Y
0
c
-1
C(-1、2) r=1
(x+1)2+(y-2)2=1
4.圆心为(1,3)并与直线3x-4y-6=0相切
例题分析
例2、△ABC的三个顶点的坐标分别是A(5,1),B(7,-3),C(2,-8),求它的外接圆的方程.
解:设的求圆的方程是(x-a)2+(y-b)2=r2
根据题意,可得
解此方程组,得 a=2 , b=-3 , r2=25
所以, △ABC的外接圆的方程是
(x-2)2+(y+3)2=25
例题分析
例3、已知圆心为C的圆经过点A(1,1)和B(2,-2) 圆心C在直线l: x-y+1=0上,求圆心为C的圆的标准方程.
y
x
O
C
A
B
l
X
Y
0
C(8、3)
P(5、1)
4、已知圆经过P(5、1),圆心在C(8、3),求圆方程.
练习
(x-8)2+(y-3)2=13
5、已知两点A(4、9)、B(6、 3), 求以AB为直径的圆的方程.
A(4、9)
B(6、3)
X
0
Y
练习
小结:
(1)、牢记: 圆的标准方程:(x-a)2+(y-b)2=r2。
(2)、明确:三个条件a、b、r确定一个圆。
(3)、方法:①待定系数法
②数形结合法
思考题:
圆的方程(x-a)2+(y-b)2=r2
展开:x2+y2-2ax-2by+(a2+b2-r2)=0
是关于x、y的二元二次方程。
那么是否二元二次方程均可化为圆方程?
怎样的二元二次方程可化为圆的方程?
(x-2)2+(y-2)2=4 或 (x+2)2+(y+2)2=4
2
0
C(2,2)
C(-2,-2)
X
Y
-2
-2
Y=X
练习
4、圆心在直线y=x上,与两轴同时相切,半径为2.
求曲线方程的步骤
1、选系
2、取动点
3、列方程
4、化简
§4.1.1 圆的标准方程
圆的定义:
怎样求出圆心是A(a,b),半径是r的圆的方程
平面内与定点距离等于定长的点的集合(轨迹)是圆.
(x-a)2+(y-b)2=r2
三个独立条件a、b、r确定一个圆的方程.
x
y
O
A
M
r
圆的标准方程:
定点就是圆心,
定长就是半径.
圆心是A(a,b),
半径是r
点M0(x0,y0)在圆(x-a)2+(y-b)2=r2上、内、外的条件是什么?
点M0在圆上
点M0在圆内
(x0-a)2+(y0-b)2=r2
(x0-a)2+(y0-b)2
点M0在圆外
例题分析
例1、写出圆心为A(2,-3),半径长等于5的圆的方程,并判断M1(5,-7),M2(4,-5), M3(6,-8)是在圆上或圆内或圆外?
1 (口答) 、求圆的圆心及半径
(1)、x2+y2=4 (2)、(x+1)2+y2=1
练习
X
y
0
+2
-2
C(0、0) r=2
X
Y
0
-1
C(-1、0) r=1
(3) (x+3)2+(y-4)2=5
(5) (x+m)2+(y-n)2=5 =a2
(4) (x+1)2+(y-4)2=(-2)2
(1) x2+y2=9
(2) (x+3)2+(y-4)2=5
练习
2、写出下列圆的方程
3、圆心在(-1、2),与y轴相切的圆
(1)圆心在原点,半径是3
(2)圆心为(-3,4),半径为
3、圆心在(-1、2),与y轴相切
X
Y
0
c
-1
C(-1、2) r=1
(x+1)2+(y-2)2=1
4.圆心为(1,3)并与直线3x-4y-6=0相切
例题分析
例2、△ABC的三个顶点的坐标分别是A(5,1),B(7,-3),C(2,-8),求它的外接圆的方程.
解:设的求圆的方程是(x-a)2+(y-b)2=r2
根据题意,可得
解此方程组,得 a=2 , b=-3 , r2=25
所以, △ABC的外接圆的方程是
(x-2)2+(y+3)2=25
例题分析
例3、已知圆心为C的圆经过点A(1,1)和B(2,-2) 圆心C在直线l: x-y+1=0上,求圆心为C的圆的标准方程.
y
x
O
C
A
B
l
X
Y
0
C(8、3)
P(5、1)
4、已知圆经过P(5、1),圆心在C(8、3),求圆方程.
练习
(x-8)2+(y-3)2=13
5、已知两点A(4、9)、B(6、 3), 求以AB为直径的圆的方程.
A(4、9)
B(6、3)
X
0
Y
练习
小结:
(1)、牢记: 圆的标准方程:(x-a)2+(y-b)2=r2。
(2)、明确:三个条件a、b、r确定一个圆。
(3)、方法:①待定系数法
②数形结合法
思考题:
圆的方程(x-a)2+(y-b)2=r2
展开:x2+y2-2ax-2by+(a2+b2-r2)=0
是关于x、y的二元二次方程。
那么是否二元二次方程均可化为圆方程?
怎样的二元二次方程可化为圆的方程?
(x-2)2+(y-2)2=4 或 (x+2)2+(y+2)2=4
2
0
C(2,2)
C(-2,-2)
X
Y
-2
-2
Y=X
练习
4、圆心在直线y=x上,与两轴同时相切,半径为2.
求曲线方程的步骤
1、选系
2、取动点
3、列方程
4、化简
