4.2.1直线与圆的位置关系(新人教A版必修2)
文档属性
| 名称 | 4.2.1直线与圆的位置关系(新人教A版必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 232.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-14 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
4.2 直线、圆的位置关系
一.复习回顾
4、点和圆的位置关系有几种?
(1)d(2)d=r 点在圆上
(3)d>r 点 在圆外
r
d
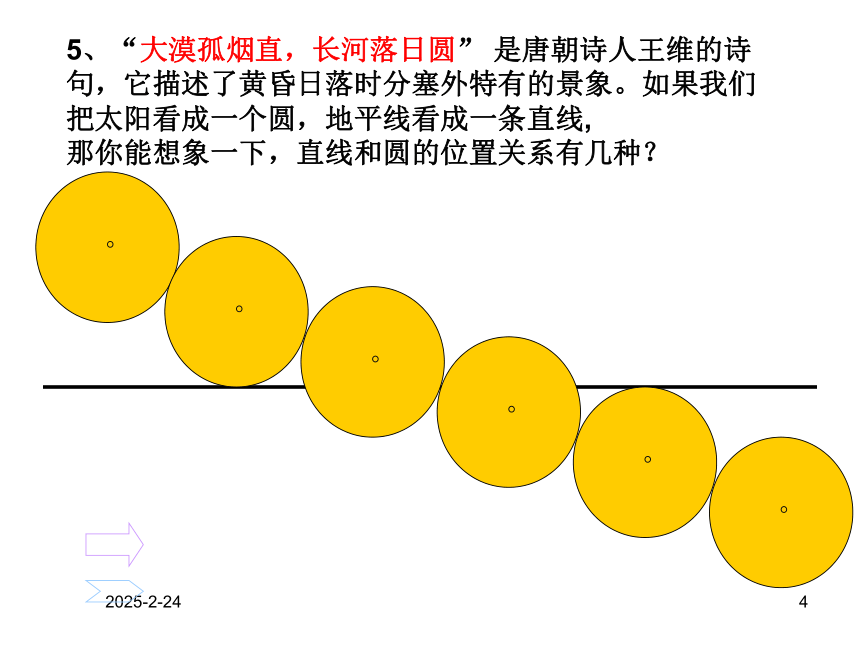
5、“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,
那你能想象一下,直线和圆的位置关系有几种?
思考:我们怎样判别直线与圆的关系
直线与圆相交
直线与圆相切
直线与圆相离
位置关系
判别方法
2个交点
1个交点
没有交点
问题:如何用直线和圆的方程判断它们之间的位置关系?
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆的位置关系的判定方法:
直线l:Ax+By+C=0
圆C:(x-a)2+(y-b)2=r2(r>0)
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
(2) 利用直线与圆的公共点的个数进行判断:
n=0
n=1
n=2
直线与圆相离
直线与圆相切
直线与圆相交
△<0
△=0
△>0
例1、如图,已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。
.
x
y
O
C
A
B
l
解法一:
所以,直线l与圆相交,有两个公共点.
例1、如图,已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。
.
x
y
O
C
A
B
l
解法二:由直线l与圆的方程,得
消去y,得
例1、如图,已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。
.
x
y
O
C
A
B
l
所以,直线l与圆有两个公共点,它们的坐标分别是A(2,0),B(1,3).
X
C(1、3)
3x-4y-6=0
Y
0
练习
1、求以c(1、3)为圆心,并和直线
3x-4y-6=0相切的圆的方程.
2、判断直线3x+4y+2=0与圆x2+y2-2x=0的位置关系.
例2、已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为 ,求直线l的方程。
.
x
y
O
M
.
E
F
例3.已知过点M(-3,-3)的直线l 被圆
所截得的弦长为 ,求 l 的方程.
解:因为直线l 过点M,可设所求直线l 的方程为:
对于圆:
如图:
,根据圆的性质,
解得:
所求直线为:
问题:一艘轮船在沿直线返回港口的 途中,接到气象台的台风预报:台风中心位于 轮船正西70km处,受影响的范围是半径长为30km的圆形区域,已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响
分析:以台风中心为原点O,东西方向为x轴,建立如图所示的直角坐标系,其中,取10km为单位长度.
问题归结为圆O与直线l 是否有交点
例3、已知圆的方程是x2+y2=r2,求经过圆
上一点M(x0,y0)的切线方程.
y
x
O
)
,
(
0
0
y
x
M
思考
1.圆的切线有哪些性质?
2.求切线方程的关键是什么?
3.切线的斜率一定存在吗?
(x-2)2+(y-2)2=4 或 (x+2)2+(y+2)2=4
2
0
C(2,2)
C(-2,-2)
X
Y
-2
-2
Y=X
练习
4、圆心在直线y=x上,与两轴同时相切,半径为2.
判别直线与圆的位置关系的方法:
直线
圆
d :圆心C (a , b)到直线 l 的距离
相交 相切 相离
公共点(交点)个数
d与r的大小关系
图象
0个
1个
2个
例题
自点 作圆 的切线
求切线 的方程
y
x
o
A
分析
方法总结:求过圆外一点所作圆的切线的方程分两种情况进行讨论:(1)直线垂直于X轴(k不存在)(2)直线不垂直于X轴(k存在)
分析:
(结合图形分析)由于本题知道了一点的坐标,可设方程为点斜式方程,用点斜式的前提是斜率存在,因此我们要首先对直线的斜率是否存在进行讨论:
1、直线垂直于X轴(斜率不存在),由图形可知直线不和圆相切
2、直线不垂直于X轴(斜率存在),由图形可知共有两条直线,求出k即可.(k有两个值)
x
o
A
y
§4.1.1 直线与圆的位置关系
4.2 直线、圆的位置关系
一.复习回顾
4、点和圆的位置关系有几种?
(1)d
(3)d>r 点 在圆外
r
d
5、“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,
那你能想象一下,直线和圆的位置关系有几种?
思考:我们怎样判别直线与圆的关系
直线与圆相交
直线与圆相切
直线与圆相离
位置关系
判别方法
2个交点
1个交点
没有交点
问题:如何用直线和圆的方程判断它们之间的位置关系?
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆的位置关系的判定方法:
直线l:Ax+By+C=0
圆C:(x-a)2+(y-b)2=r2(r>0)
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
(2) 利用直线与圆的公共点的个数进行判断:
n=0
n=1
n=2
直线与圆相离
直线与圆相切
直线与圆相交
△<0
△=0
△>0
例1、如图,已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。
.
x
y
O
C
A
B
l
解法一:
所以,直线l与圆相交,有两个公共点.
例1、如图,已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。
.
x
y
O
C
A
B
l
解法二:由直线l与圆的方程,得
消去y,得
例1、如图,已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。
.
x
y
O
C
A
B
l
所以,直线l与圆有两个公共点,它们的坐标分别是A(2,0),B(1,3).
X
C(1、3)
3x-4y-6=0
Y
0
练习
1、求以c(1、3)为圆心,并和直线
3x-4y-6=0相切的圆的方程.
2、判断直线3x+4y+2=0与圆x2+y2-2x=0的位置关系.
例2、已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为 ,求直线l的方程。
.
x
y
O
M
.
E
F
例3.已知过点M(-3,-3)的直线l 被圆
所截得的弦长为 ,求 l 的方程.
解:因为直线l 过点M,可设所求直线l 的方程为:
对于圆:
如图:
,根据圆的性质,
解得:
所求直线为:
问题:一艘轮船在沿直线返回港口的 途中,接到气象台的台风预报:台风中心位于 轮船正西70km处,受影响的范围是半径长为30km的圆形区域,已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响
分析:以台风中心为原点O,东西方向为x轴,建立如图所示的直角坐标系,其中,取10km为单位长度.
问题归结为圆O与直线l 是否有交点
例3、已知圆的方程是x2+y2=r2,求经过圆
上一点M(x0,y0)的切线方程.
y
x
O
)
,
(
0
0
y
x
M
思考
1.圆的切线有哪些性质?
2.求切线方程的关键是什么?
3.切线的斜率一定存在吗?
(x-2)2+(y-2)2=4 或 (x+2)2+(y+2)2=4
2
0
C(2,2)
C(-2,-2)
X
Y
-2
-2
Y=X
练习
4、圆心在直线y=x上,与两轴同时相切,半径为2.
判别直线与圆的位置关系的方法:
直线
圆
d :圆心C (a , b)到直线 l 的距离
相交 相切 相离
公共点(交点)个数
d与r的大小关系
图象
0个
1个
2个
例题
自点 作圆 的切线
求切线 的方程
y
x
o
A
分析
方法总结:求过圆外一点所作圆的切线的方程分两种情况进行讨论:(1)直线垂直于X轴(k不存在)(2)直线不垂直于X轴(k存在)
分析:
(结合图形分析)由于本题知道了一点的坐标,可设方程为点斜式方程,用点斜式的前提是斜率存在,因此我们要首先对直线的斜率是否存在进行讨论:
1、直线垂直于X轴(斜率不存在),由图形可知直线不和圆相切
2、直线不垂直于X轴(斜率存在),由图形可知共有两条直线,求出k即可.(k有两个值)
x
o
A
y
§4.1.1 直线与圆的位置关系
