人教版九年级上册 第22章 二次函数 经典专题88题(共102张)
文档属性
| 名称 | 人教版九年级上册 第22章 二次函数 经典专题88题(共102张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 18:23:17 | ||
图片预览






文档简介
(共102张PPT)
一、选择题
2.函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
A
.
m,n是常数,且m≠0
B
.
m,n是常数,且n≠0
C.
m,n是常数,且m≠n
D
.
m,n为任何实数
C
1.下列函数是二次函数的是
(
)
A.y=2x+1
B.
C.y=3x2+1
D.
C
3.
二次函数y=-3x2+1的图象是将( )
A.抛物线y=-3x2向左平移3个单位得到
B.抛物线y=-3x2向左平移1个单位得到
C.抛物线y=3x2向上平移1个单位得到
D.抛物线y=-3x2向上平移1个单位得到
解析:二次函数y=-3x2+1的图象是将抛物线y=-3x2向上平移1个单位得到的.故选D.
D
C
D
D
D
A
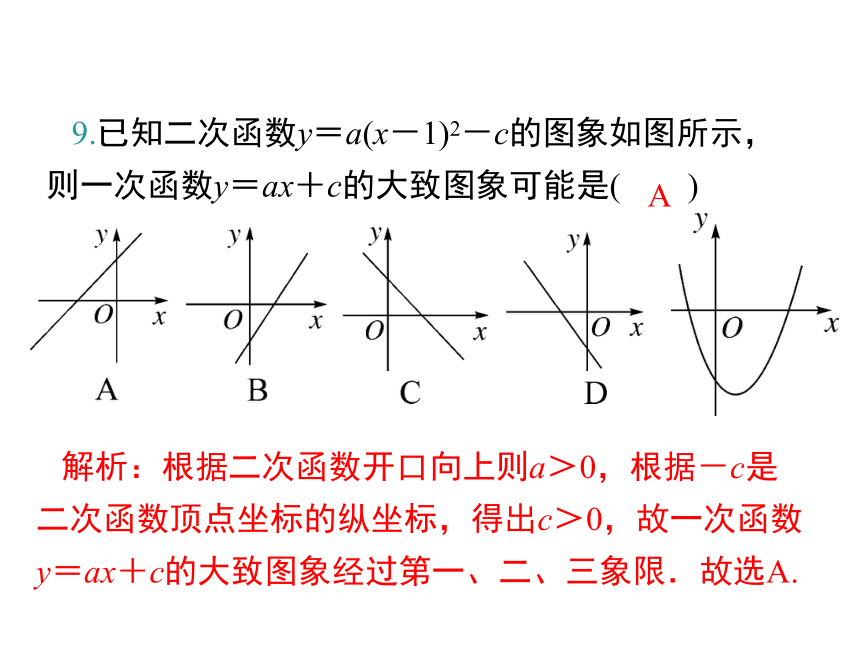
9.已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
解析:根据二次函数开口向上则a>0,根据-c是二次函数顶点坐标的纵坐标,得出c>0,故一次函数y=ax+c的大致图象经过第一、二、三象限.故选A.
A
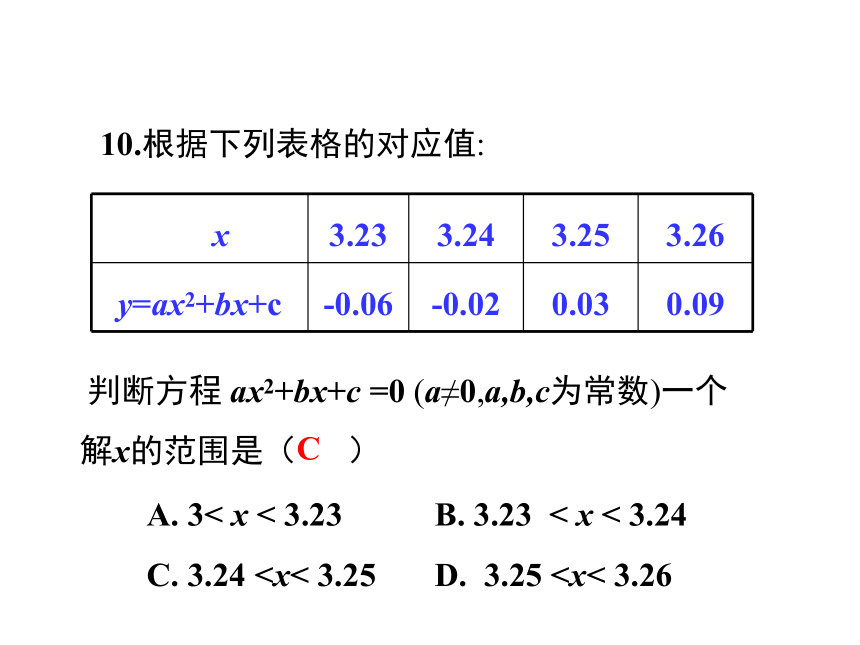
判断方程
ax2+bx+c
=0
(a≠0,a,b,c为常数)一个解x的范围是(
)
A.
3<
x
<
3.23
B.
3.23
<
x
<
3.24
C.
3.24
3.25
D.
3.25
3.26
x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
10.根据下列表格的对应值:
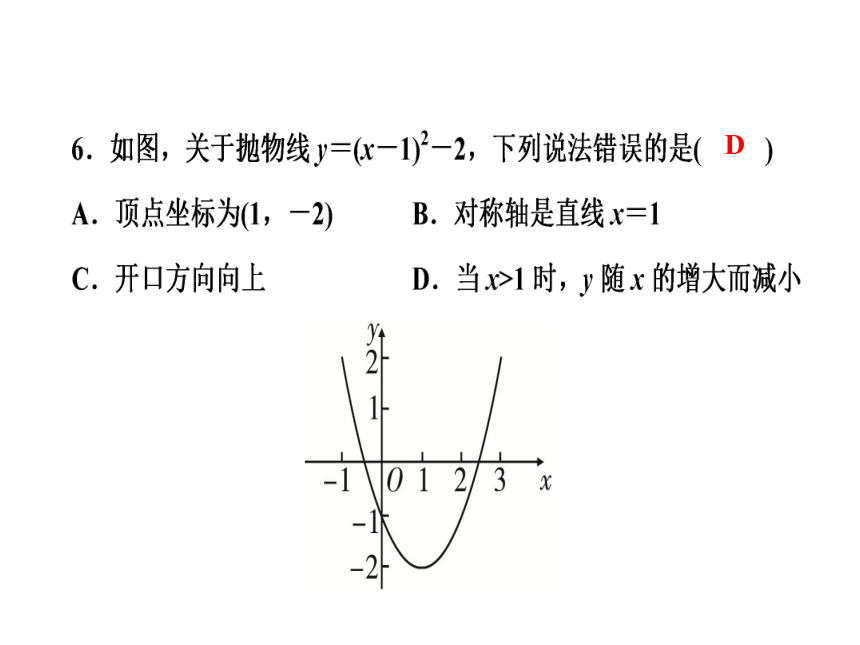
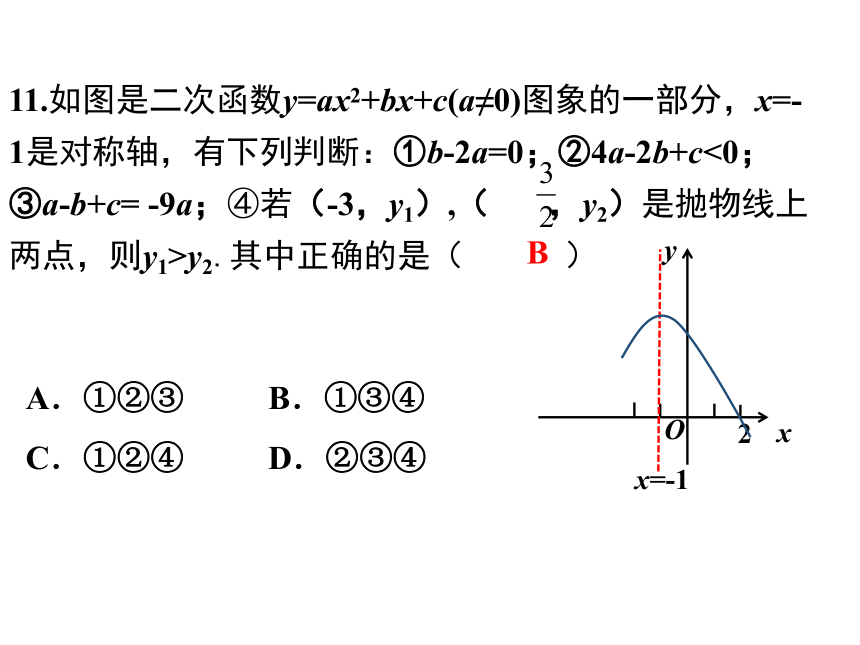
11.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=
-9a;④若(-3,y1),(
,y2)是抛物线上两点,则y1>y2.其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.②③④
x
y
O
2
x=-1
B
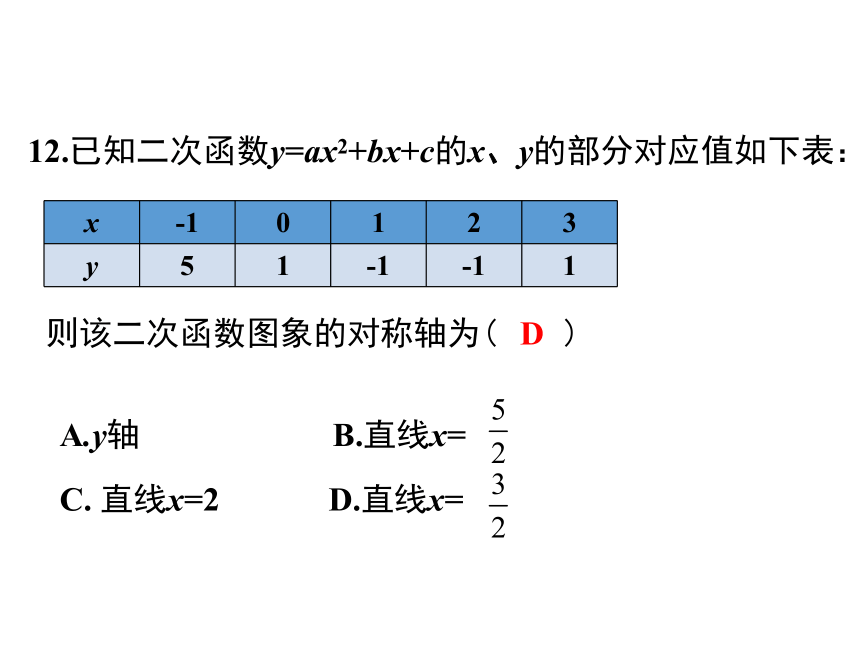
12.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x
-1
0
1
2
3
y
5
1
-1
-1
1
A.y轴
B.直线x=
C.
直线x=2
D.直线x=
则该二次函数图象的对称轴为(
)
D
13.若一元二次方程
无实根,则抛物线
图象位于(
)
A.x轴上方
B.第一、二、三象限
C.x轴下方
D.第二、三、四象限
A
14.二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3
B.k<3且k≠0
C.k≤3
D.k≤3且k≠0
D
15.已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是(
)
A.b≥-1
B.b≤-1
C.b≥1
D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴
,即b≤1,故选择D
.
D
D
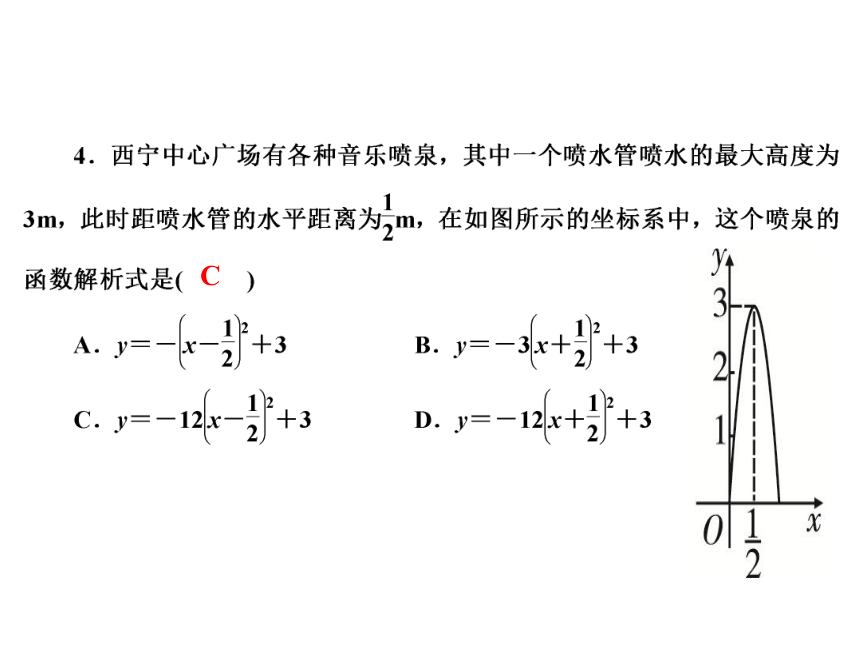
3.
17.
某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.
A.50m
B.100m
C.160m
D.200m
C
18.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的图象大致为( )
方法总结:熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.
D
B
B
20:已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似根为( )
A.x1≈-2.1,x2≈0.1
B.x1≈-2.5,x2≈0.5
C.x1≈-2.9,x2≈0.9
D.x1≈-3,x2≈1
解析:由图象可得二次函数y=ax2+bx+c图象的对称轴为x=-1,而对称轴右侧图象与x轴交点到原点的距离约为0.5,∴x2≈0.5;又∵对称轴为x=-1,则
=-1,∴x1=2×(-1)-0.5=-2.5.故x1≈-2.5,x2≈0.5.故选B.
B
21.已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2.
其中正确的个数是
( )
A.1 B.2 C.3 D.4
D
由图象上横坐标为
x=-2的点在第三象限可得4a-2b+c<0,故③正确;
由图象上x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出
a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.
【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得
c>0,则abc>0,故①正确;
由对称轴x>-1可得2a-b<0,故②正确;
22.如图,平面直角坐标系中,函数图象的表达式应是
.
x
y
O
1
2
-1
-2
-3
-4
3
2
1
-1
3
4
5
二、填空题
23.
已知函数
y=3x2m-1-5
(1)
当m=__时,y是关于x的一次函数;
(2)
当m=__时,y是关于x的二次函数
.
1
24.对于二次函数y=(m+1)xm2-m+3,当x>0时y随x的增大而增大,则m=____.
25.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)
则a=____.
26.抛物线y=ax2+c与x轴交于A(-2,0)﹑B两点,与y轴交于点C(0,-4),则三角形ABC的面积是_______.
2
-2
8
27.把抛物线y=-x2沿着x轴方向平移3个单位长度,那么平移后抛物线的解析式是
.
28.二次函数y=2(x-
)2图象的对称轴是直线_______,顶点是________.
29
.若(-
,y1)(-
,y2)(
,y3)为二次函数y=(x-2)2图象上的三点,则y1
,y2
,y3的大小关系为_______________.
y=-(x+3)2或y=-(x-3)2
y1
>y2
>
y3
30.把抛物线y=-3x2先向上平移2个单位,再向右平移1
个单位,那么所得抛物线是___________________.
.
31.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为______________
下
(2,13)
直线x=2
x>3或x<-1
32.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在
s后落地.
4
33.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为为
那么铅球运动过程中最高点离地面的距离为
米.
x
y
O
2
③④⑤
15
20
37.若二次函数y=-x2+2x+k的部分图象如图所示,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2=
;
-1
y
O
x
1
3
38.一元二次方程
3x2+x-10=0的两个根是x1=-2
,x2=
,那么二次函数
y=
3x2+x-10与x轴的交点坐标是
.
(-2,0)
(
,0)
39.函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是
______________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
3
-1
O
x
2
(4,2)
(-2,2)
x1=-2,
x2=4
x<-2或x>4
-2y
40.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20
≤x
≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为
元.
25
m>0
足球离开地面后落地时间
2
19.6m
y=-x2+x+2
44.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为
.每月利润w(元)与衬衣售价x(元)之间的函数关系式为
.(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
45.
已知
函数
(1)m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
第(2)问易忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案,需要引起同学们的重视.
注意
三、解答题
46.已知:
,k取什么值时,y是x的二次函数?
解:当
=2且k+2≠0,即k=-2时,
y是x的二次函数.
解:
由题意得:
∴m≠±3
48.
一个二次函数
.
(1)求k的值.
(2)当x=0.5时,y的值是多少?
解:
(1)由题意,得
解得
将x=0.5代入函数关系式
.
(2)当k=2时,
49.若函数
是二次函数,求:
(1)求a的值.
(2)
求函数关系式.
(3)当x=-2时,y的值是多少?
解:
(1)由题意,得
解得
(2)当a=-1时,函数关系式为
.
(3)将x=-2代入函数关系式中,有
57.
某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
解:建立如图所示的坐标系,
根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
●B(1,2.25)
(0,1.25)
●
C
●
D
o
A
x
y
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0)
;
同理,点
D的坐标为(-2.5,0)
.
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=-
(x-1)2+2.25.
●B(1,2.25)
(0,1.25)
●
D
o
A
x
y
●
C
58.
有一座抛物线形拱桥,正常水位时桥下水面宽度为
20
m,拱顶距离水面
4
m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20
m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
59。如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:如图,建立直角坐标系.
则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
x
y
O
解得
a=-0.2,
k=3.5,
设以y轴为对称轴的抛物线的解析式为
y=a(x-0)2+k
,
即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=-0.2x2+3.5.
当
x=-2.5时,y=2.25
.
故该运动员出手时的高度为2.25m.
2.25a+k=3.05,
k=3.5,
x
y
O
60.
某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系怎样表示?
分析:这种产品的原产量是20件,
一年后的产量是
件,再经过一年后的产量是
件,即两年后的产量y=________.
20(1+x)
20(1+x)2
20(1+x)2
答:
y=20x2+40x+20;
此式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有唯一的一个对应值,即y是x的函数.
61.
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件,当销售单价为多少元时,该店能在一个月内获得最大利润?
①每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,填空:
单件利润(元)
销售量(件)
每月利润(元)
正常销售
涨价销售
10
180
10+x
180-10x
y=(10+x)(180-10x)
1800
建立函数关系式:y=(10+x)(180-10x),
即:y=-10x2+80x+1800.
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故180-10x
≥0,因此自变量的取值范围是
x
≤18.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+80x+1800
=-10(x-4)2+1960.
当x=4时,即销售单价为34元时,y取最大值1960元.
答:当销售单价为34元时,该店在一个月内能获得最
大利润1960元.
②自变量x的取值范围如何确定?
62.一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
w=[12+2(x-1)][80-4(x-1)]
=(10+2x)(84-4x)
=-8x2+128x+840
=-8(x-8)2+1352.
解:设生产x档次的产品时,每天所获得的利润为w元,
则
当x=8时,w有最大值,且w最大=1352.
答:该工艺师生产第8档次产品,可使利润最大,
最大利润为1352.
x
y
5
16
O
7
63.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由题中条件可求y=-x2+20x-75
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最
大,为25元;
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
(2)由对称性知y=16时,x=7和13.
故销售单价在7
≤x
≤13时,利润不低于16元.
64:已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:此抛物线与x轴总有两个交点;
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.
(1)证明:∵m≠0,
∴Δ=(m+2)2-4m×2=m2+4m+4-8m=(m-2)2.
∵(m-2)2≥0,
∴Δ≥0,
∴此抛物线与x轴总有两个交点;
(2)解:令y=0,则(x-1)(mx-2)=0,
所以
x-1=0或mx-2=0,
解得
x1=1,x2=
.
当m为正整数1或2时,x2为整数,即抛物线与x轴总有两个交点,且它们的横坐标都是整数.
所以正整数m的值为1或2.
65:已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:此抛物线与x轴总有两个交点;
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.
66:已知:抛物线y=x2+ax+a-2.
(1)求证:不论a取何值时,抛物线y=x2+ax+a-2与x轴都有两个不同的交点;
(2)设这个二次函数的图象与x轴相交于A(x1,0),B(x2,0),且x1、x2的平方和为3,求a的值.
(1)证明:∵Δ=a2-4(a-2)=(a-2)2+4>0,
∴不论a取何值时,抛物线y=x2+ax+a-2与x轴都有两个不同的交点;
(2)解:∵x1+x2=-a,x1·x2=a-2,
∴x1(2)+x2(2)=(x1+x2)2-2x1·x2=a2-2a+4=3,
∴a=1.
67.如图,丁丁在扔铅球时,铅球沿抛物线
运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.
(1)当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
(3)铅球离地面的高度能否达
到3m?为什么?
解
(1)由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.1m时,它离初始
位置的水平距离是1m或5m.
(1)当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
(2)由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.5m时,它离初始位
置的水平距离是3m.
(3)由抛物线的表达式得
即
因为
所以方程无实根.
所以铅球离地面的高度不能达到3m.
(3)铅球离地面的高度能否达到3m?为什么?
68.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.
解:当k=3时,函数y=2x+1是一次函数.
∵一次函数y=2x+1与x轴有一个交点,
∴k=3;
当k≠3时,y=(k-3)x2+2x+1是二次函数.
∵二次函数y=(k-3)x2+2x+1的图象与x轴有交点,
∴Δ=b2-4ac≥0.
∵b2-4ac=22-4(k-3)=-4k+16,
∴-4k+16≥0.∴k≤4且k≠3.
综上所述,k的取值范围是k≤4.
69.某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面
米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
解:(1)由条件可得到出手点、最高点和篮框的坐标分别为A(0,
),B(4,4),C(7,3),其中B是抛物线的顶点.
设二次函数关系式为y=a(x-h)2+k,将点A、B的坐标代入,可得y=-
(x-4)2+4.
将点C的坐标代入上式,得左边=3,右边=-
(7-4)2+4=3,左边=右边,即点C在抛物线上.所以此球一定能投中;
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
(2)将x=1代入函数关系式,得y=3.
因为3.1>3,所以盖帽能获得成功.
70.已知二次函数
的图象,利用图象回答问题:
(1)方程
的解是什么?
(2)x取什么值时,y>0
?
(3)x取什么值时,y<0
?
x
y
O
2
4
8
解:(1)x1=2,x2=4;
(2)x<2或x>4;
(3)271.
一个二次函数的图象经过
(0,
1)、(2,4)、(3,10)三点,求这个二次函数的表达式.
解:
设这个二次函数的表达式是y=ax2+bx+c,由于这个函数经过点(0,
1),可得c=1.
又由于其图象经过(2,4)、(3,10)两点,可得
4a+2b+1=4,
9a+3b+1=10,
解这个方程组,得
∴所求的二次函数的表达式是
72.
一个二次函数的图象经点
(0,
1),它的顶点坐标为(8,9),求这个二次函数的表达式.
解:
因为这个二次函数的图象的顶点坐标为(8,9),因此,可以设函数表达式为
y=a(x-8)2+9.
又由于它的图象经过点(0
,1),可得
0=a(0-8)2+9.
解得
∴所求的二次函数的解析式是
解:∵(-3,0)(-1,0)是抛物线y=ax2+bx+c与x轴的交点.所以可设这个二次函数的表达式是y=a(x-x1)(x-x2).(其中x1、x2为交点的横坐标.因此得
y=a(x+3)(x+1).
再把点(0,-3)代入上式得
∴a(0+3)(0+1)=-3,
解得a=-1,
∴所求的二次函数的表达式是
y=-(x+3)(x+1),即y=-x2-4x-3.
73.选取(-3,0),(-1,0),(0,-3),试出这个二次函数的表达式.
x
y
O
1
2
-1
-2
-3
-4
-1
-2
-3
-4
-5
1
2
74.请回答抛物线y
=
4(x-3)2+7由抛物线y=4x2怎样平移得到?
由抛物线向上平移7个单位再向右平移3个单位得到的.
71.如果一条抛物线的形状与
形状相同,且顶点坐标是(4,-2),试求这个函数关系式.
75.已知二次函数y=ax2
+
c的图象经过点(2,3)
和(-1,-3),求这个二次函数的表达式.
解:∵该图象经过点(2,3)和(-1,-3),
3=4a+c,
-3=a+c,
∴所求二次函数表达式为
y=2x2-5.
∴{
a=2,
c=-5.
解得
{
76.已知二次函数y=ax2
+
bx的图象经过点(-2,8)
和(-1,5),求这个二次函数的表达式.
解:∵该图象经过点(-2,8)和(-1,5),
8=4a-2b,
5=a-b,
∴{
解得a=-1,b=-6.
∴
y=-x2-6x.
77.已知二次函数的图象经过点(-1,-5),(0,-4)和(1,1).求这个二次函数的表达式.
解:设这个二次函数的表达式为y=ax2+bx+c.
依题意得
∴这个二次函数的表达式为y=2x2+3x-4.
a+b+c=1,
c=-4,
a-b+c=-5,
解得
b=3,
c=-4,
a=2,
78.已知抛物线与x轴相交于点A(-1,0),B(1,0),且过点M(0,1),求此函数的表达式.
解:因为点A(-1,0),B(1,0)是图象与x轴的交点,所以设二次函数的表达式为y=a(x+1)(x-1).
又因为抛物线过点M(0,1),
所以1=a(0+1)(0-1),解得a=-1,
所以所求抛物线的表达式为y=-(x+1)(x-1),
即y=-x2+1.
79.如图,抛物线y=x2+bx+c过点A(-4,-3),与y轴交于点B,对称轴是x=-3,请解答下列问题:
(1)求抛物线的表达式;
解:(1)把点A(-4,-3)代入y=x2+bx+c
得16-4b+c=-3,c-4b=-19.
∵对称轴是x=-3,∴
=-3,
∴b=6,∴c=5,
∴抛物线的表达式是y=x2+6x+5;
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.
(2)∵CD∥x轴,∴点C与点D关于x=-3对称.
∵点C在对称轴左侧,且CD=8,
∴点C的横坐标为-7,
∴点C的纵坐标为(-7)2+6×(-7)+5=12.
∵点B的坐标为(0,5),
∴△BCD中CD边上的高为12-5=7,
∴△BCD的面积=
×8×7=28.
80.
已知二次函数y=a(x-1)2-4的图象经过点(3,0).
(1)求a的值;
(2)若A(m,y1)、B(m+n,y2)(n>0)是该函数图象上的两点,当y1=y
2时,求m、n之间的数量关系.
解:(1)将(3,0)代入y=a(x-1)2-4,
得0=4a-4,解得a=1;
(2)方法一:
根据题意,得y1=(m-1)2-4,y2=(m+n-1)2-4,
∵y1=y2,
∴(m-1)2-4=(m+n-1)2-4,即(m-1)2=(m+n-1)2.
∵n>0,∴m-1=-(m+n-1),化简,得2m+n=2;
方法二:
∵函数y=(x-1)2-4的图象的对称轴是经过点(1,-4),且平行于y轴的直线,
∴m+n-1=1-m,化简,得
2m+n=2.
方法总结:已知函数图象上的点,则这点的坐标必满足函数的表达式,代入即可求得函数解析式.
81.
要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
C(3,0)
B(1,3)
A
x
O
y
1
2
3
1
2
3
解:如图建立直角坐标系,
点(1,3)是图中这段抛物线的顶点.
因此可设这段抛物线对应的函数是
∵这段抛物线经过点(3,0),
∴
0=a(3-1)2+3.
解得:
因此抛物线的解析式为:
y=a(x-1)2+3
(0≤x≤3).
当x=0时,y=2.25.
答:水管长应为2.25m.
3
4
a=-
y=
(x-1)2+3
(0≤x≤3)
3
4
-
O
y
x
–1
–2
3
82.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a、b同号;
(2)当x=–1和x=3时,函数值相等;
(3)
4a+b=0;
(4)当y=–2时,x的值只能取0;
其中正确的是
.
直线x=1
(2)
83.
如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴
×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=±
,
此时P点坐标为(
,2),(-
,2);
当b=-2时,x2-4=-2,解得x=±
,
此时P点坐标为(
,2),(-
,2).
84.
抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2,
,
∴平移后二次函数关系式为y=
(x-3)2.
方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
85:如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴
×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=±
,
此时P点坐标为(
,2),(-
,2);
当b=-2时,x2-4=-2,解得x=±
,
此时P点坐标为(
,2),(-
,2).
86.矩形的周长为16cm,它的一边长为x(cm),面积为y(cm2).求
(1)y与x之间的函数解析式及自变量x的取值范围;
(2)当x=3时矩形的面积.
解:(1)y=(8-x)x=-x2+8x
(0<x<8);
(2)当x=3时,y=-32+8×3=15
cm2
.
87:某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
解:由题意可得
-10x2+180x+400=1120,
整理得
x2-18x+72=0,
解得
x1=6,x2=12(舍去).
所以,该产品的质量档次为第6档.
【方法总结】解决此类问题的关键是要吃透题意,确定变量,建立函数模型.
88.某商店经销一种销售成本为每千克40元的商品,根据市场分析,若按每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量
就减少10kg,针对这种商品的销售情况,请解答下列问题:
(1)当销售单价为每千克55元时,计算月销售量和销售利润分别为多少?
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出自变量x的取值范围)
一、选择题
2.函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
A
.
m,n是常数,且m≠0
B
.
m,n是常数,且n≠0
C.
m,n是常数,且m≠n
D
.
m,n为任何实数
C
1.下列函数是二次函数的是
(
)
A.y=2x+1
B.
C.y=3x2+1
D.
C
3.
二次函数y=-3x2+1的图象是将( )
A.抛物线y=-3x2向左平移3个单位得到
B.抛物线y=-3x2向左平移1个单位得到
C.抛物线y=3x2向上平移1个单位得到
D.抛物线y=-3x2向上平移1个单位得到
解析:二次函数y=-3x2+1的图象是将抛物线y=-3x2向上平移1个单位得到的.故选D.
D
C
D
D
D
A
9.已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
解析:根据二次函数开口向上则a>0,根据-c是二次函数顶点坐标的纵坐标,得出c>0,故一次函数y=ax+c的大致图象经过第一、二、三象限.故选A.
A
判断方程
ax2+bx+c
=0
(a≠0,a,b,c为常数)一个解x的范围是(
)
A.
3<
x
<
3.23
B.
3.23
<
x
<
3.24
C.
3.24
D.
3.25
x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
10.根据下列表格的对应值:
11.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=
-9a;④若(-3,y1),(
,y2)是抛物线上两点,则y1>y2.其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.②③④
x
y
O
2
x=-1
B
12.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x
-1
0
1
2
3
y
5
1
-1
-1
1
A.y轴
B.直线x=
C.
直线x=2
D.直线x=
则该二次函数图象的对称轴为(
)
D
13.若一元二次方程
无实根,则抛物线
图象位于(
)
A.x轴上方
B.第一、二、三象限
C.x轴下方
D.第二、三、四象限
A
14.二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3
B.k<3且k≠0
C.k≤3
D.k≤3且k≠0
D
15.已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是(
)
A.b≥-1
B.b≤-1
C.b≥1
D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴
,即b≤1,故选择D
.
D
D
3.
17.
某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.
A.50m
B.100m
C.160m
D.200m
C
18.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的图象大致为( )
方法总结:熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.
D
B
B
20:已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似根为( )
A.x1≈-2.1,x2≈0.1
B.x1≈-2.5,x2≈0.5
C.x1≈-2.9,x2≈0.9
D.x1≈-3,x2≈1
解析:由图象可得二次函数y=ax2+bx+c图象的对称轴为x=-1,而对称轴右侧图象与x轴交点到原点的距离约为0.5,∴x2≈0.5;又∵对称轴为x=-1,则
=-1,∴x1=2×(-1)-0.5=-2.5.故x1≈-2.5,x2≈0.5.故选B.
B
21.已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2.
其中正确的个数是
( )
A.1 B.2 C.3 D.4
D
由图象上横坐标为
x=-2的点在第三象限可得4a-2b+c<0,故③正确;
由图象上x=1的点在第四象限得a+b+c<0,由图象上x=-1的点在第二象限得出
a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.
【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得
c>0,则abc>0,故①正确;
由对称轴x>-1可得2a-b<0,故②正确;
22.如图,平面直角坐标系中,函数图象的表达式应是
.
x
y
O
1
2
-1
-2
-3
-4
3
2
1
-1
3
4
5
二、填空题
23.
已知函数
y=3x2m-1-5
(1)
当m=__时,y是关于x的一次函数;
(2)
当m=__时,y是关于x的二次函数
.
1
24.对于二次函数y=(m+1)xm2-m+3,当x>0时y随x的增大而增大,则m=____.
25.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)
则a=____.
26.抛物线y=ax2+c与x轴交于A(-2,0)﹑B两点,与y轴交于点C(0,-4),则三角形ABC的面积是_______.
2
-2
8
27.把抛物线y=-x2沿着x轴方向平移3个单位长度,那么平移后抛物线的解析式是
.
28.二次函数y=2(x-
)2图象的对称轴是直线_______,顶点是________.
29
.若(-
,y1)(-
,y2)(
,y3)为二次函数y=(x-2)2图象上的三点,则y1
,y2
,y3的大小关系为_______________.
y=-(x+3)2或y=-(x-3)2
y1
>y2
>
y3
30.把抛物线y=-3x2先向上平移2个单位,再向右平移1
个单位,那么所得抛物线是___________________.
.
31.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为______________
下
(2,13)
直线x=2
x>3或x<-1
32.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在
s后落地.
4
33.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为为
那么铅球运动过程中最高点离地面的距离为
米.
x
y
O
2
③④⑤
15
20
37.若二次函数y=-x2+2x+k的部分图象如图所示,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2=
;
-1
y
O
x
1
3
38.一元二次方程
3x2+x-10=0的两个根是x1=-2
,x2=
,那么二次函数
y=
3x2+x-10与x轴的交点坐标是
.
(-2,0)
(
,0)
39.函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是
______________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
3
-1
O
x
2
(4,2)
(-2,2)
x1=-2,
x2=4
x<-2或x>4
-2
40.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20
≤x
≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为
元.
25
m>0
足球离开地面后落地时间
2
19.6m
y=-x2+x+2
44.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为
.每月利润w(元)与衬衣售价x(元)之间的函数关系式为
.(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
45.
已知
函数
(1)m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
第(2)问易忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案,需要引起同学们的重视.
注意
三、解答题
46.已知:
,k取什么值时,y是x的二次函数?
解:当
=2且k+2≠0,即k=-2时,
y是x的二次函数.
解:
由题意得:
∴m≠±3
48.
一个二次函数
.
(1)求k的值.
(2)当x=0.5时,y的值是多少?
解:
(1)由题意,得
解得
将x=0.5代入函数关系式
.
(2)当k=2时,
49.若函数
是二次函数,求:
(1)求a的值.
(2)
求函数关系式.
(3)当x=-2时,y的值是多少?
解:
(1)由题意,得
解得
(2)当a=-1时,函数关系式为
.
(3)将x=-2代入函数关系式中,有
57.
某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
解:建立如图所示的坐标系,
根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
●B(1,2.25)
(0,1.25)
●
C
●
D
o
A
x
y
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0)
;
同理,点
D的坐标为(-2.5,0)
.
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=-
(x-1)2+2.25.
●B(1,2.25)
(0,1.25)
●
D
o
A
x
y
●
C
58.
有一座抛物线形拱桥,正常水位时桥下水面宽度为
20
m,拱顶距离水面
4
m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20
m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
59。如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:如图,建立直角坐标系.
则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
x
y
O
解得
a=-0.2,
k=3.5,
设以y轴为对称轴的抛物线的解析式为
y=a(x-0)2+k
,
即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=-0.2x2+3.5.
当
x=-2.5时,y=2.25
.
故该运动员出手时的高度为2.25m.
2.25a+k=3.05,
k=3.5,
x
y
O
60.
某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系怎样表示?
分析:这种产品的原产量是20件,
一年后的产量是
件,再经过一年后的产量是
件,即两年后的产量y=________.
20(1+x)
20(1+x)2
20(1+x)2
答:
y=20x2+40x+20;
此式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有唯一的一个对应值,即y是x的函数.
61.
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件,当销售单价为多少元时,该店能在一个月内获得最大利润?
①每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,填空:
单件利润(元)
销售量(件)
每月利润(元)
正常销售
涨价销售
10
180
10+x
180-10x
y=(10+x)(180-10x)
1800
建立函数关系式:y=(10+x)(180-10x),
即:y=-10x2+80x+1800.
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故180-10x
≥0,因此自变量的取值范围是
x
≤18.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+80x+1800
=-10(x-4)2+1960.
当x=4时,即销售单价为34元时,y取最大值1960元.
答:当销售单价为34元时,该店在一个月内能获得最
大利润1960元.
②自变量x的取值范围如何确定?
62.一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
w=[12+2(x-1)][80-4(x-1)]
=(10+2x)(84-4x)
=-8x2+128x+840
=-8(x-8)2+1352.
解:设生产x档次的产品时,每天所获得的利润为w元,
则
当x=8时,w有最大值,且w最大=1352.
答:该工艺师生产第8档次产品,可使利润最大,
最大利润为1352.
x
y
5
16
O
7
63.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由题中条件可求y=-x2+20x-75
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最
大,为25元;
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
(2)由对称性知y=16时,x=7和13.
故销售单价在7
≤x
≤13时,利润不低于16元.
64:已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:此抛物线与x轴总有两个交点;
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.
(1)证明:∵m≠0,
∴Δ=(m+2)2-4m×2=m2+4m+4-8m=(m-2)2.
∵(m-2)2≥0,
∴Δ≥0,
∴此抛物线与x轴总有两个交点;
(2)解:令y=0,则(x-1)(mx-2)=0,
所以
x-1=0或mx-2=0,
解得
x1=1,x2=
.
当m为正整数1或2时,x2为整数,即抛物线与x轴总有两个交点,且它们的横坐标都是整数.
所以正整数m的值为1或2.
65:已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:此抛物线与x轴总有两个交点;
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.
66:已知:抛物线y=x2+ax+a-2.
(1)求证:不论a取何值时,抛物线y=x2+ax+a-2与x轴都有两个不同的交点;
(2)设这个二次函数的图象与x轴相交于A(x1,0),B(x2,0),且x1、x2的平方和为3,求a的值.
(1)证明:∵Δ=a2-4(a-2)=(a-2)2+4>0,
∴不论a取何值时,抛物线y=x2+ax+a-2与x轴都有两个不同的交点;
(2)解:∵x1+x2=-a,x1·x2=a-2,
∴x1(2)+x2(2)=(x1+x2)2-2x1·x2=a2-2a+4=3,
∴a=1.
67.如图,丁丁在扔铅球时,铅球沿抛物线
运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.
(1)当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
(3)铅球离地面的高度能否达
到3m?为什么?
解
(1)由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.1m时,它离初始
位置的水平距离是1m或5m.
(1)当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
(2)由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.5m时,它离初始位
置的水平距离是3m.
(3)由抛物线的表达式得
即
因为
所以方程无实根.
所以铅球离地面的高度不能达到3m.
(3)铅球离地面的高度能否达到3m?为什么?
68.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.
解:当k=3时,函数y=2x+1是一次函数.
∵一次函数y=2x+1与x轴有一个交点,
∴k=3;
当k≠3时,y=(k-3)x2+2x+1是二次函数.
∵二次函数y=(k-3)x2+2x+1的图象与x轴有交点,
∴Δ=b2-4ac≥0.
∵b2-4ac=22-4(k-3)=-4k+16,
∴-4k+16≥0.∴k≤4且k≠3.
综上所述,k的取值范围是k≤4.
69.某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面
米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
解:(1)由条件可得到出手点、最高点和篮框的坐标分别为A(0,
),B(4,4),C(7,3),其中B是抛物线的顶点.
设二次函数关系式为y=a(x-h)2+k,将点A、B的坐标代入,可得y=-
(x-4)2+4.
将点C的坐标代入上式,得左边=3,右边=-
(7-4)2+4=3,左边=右边,即点C在抛物线上.所以此球一定能投中;
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
(2)将x=1代入函数关系式,得y=3.
因为3.1>3,所以盖帽能获得成功.
70.已知二次函数
的图象,利用图象回答问题:
(1)方程
的解是什么?
(2)x取什么值时,y>0
?
(3)x取什么值时,y<0
?
x
y
O
2
4
8
解:(1)x1=2,x2=4;
(2)x<2或x>4;
(3)2
一个二次函数的图象经过
(0,
1)、(2,4)、(3,10)三点,求这个二次函数的表达式.
解:
设这个二次函数的表达式是y=ax2+bx+c,由于这个函数经过点(0,
1),可得c=1.
又由于其图象经过(2,4)、(3,10)两点,可得
4a+2b+1=4,
9a+3b+1=10,
解这个方程组,得
∴所求的二次函数的表达式是
72.
一个二次函数的图象经点
(0,
1),它的顶点坐标为(8,9),求这个二次函数的表达式.
解:
因为这个二次函数的图象的顶点坐标为(8,9),因此,可以设函数表达式为
y=a(x-8)2+9.
又由于它的图象经过点(0
,1),可得
0=a(0-8)2+9.
解得
∴所求的二次函数的解析式是
解:∵(-3,0)(-1,0)是抛物线y=ax2+bx+c与x轴的交点.所以可设这个二次函数的表达式是y=a(x-x1)(x-x2).(其中x1、x2为交点的横坐标.因此得
y=a(x+3)(x+1).
再把点(0,-3)代入上式得
∴a(0+3)(0+1)=-3,
解得a=-1,
∴所求的二次函数的表达式是
y=-(x+3)(x+1),即y=-x2-4x-3.
73.选取(-3,0),(-1,0),(0,-3),试出这个二次函数的表达式.
x
y
O
1
2
-1
-2
-3
-4
-1
-2
-3
-4
-5
1
2
74.请回答抛物线y
=
4(x-3)2+7由抛物线y=4x2怎样平移得到?
由抛物线向上平移7个单位再向右平移3个单位得到的.
71.如果一条抛物线的形状与
形状相同,且顶点坐标是(4,-2),试求这个函数关系式.
75.已知二次函数y=ax2
+
c的图象经过点(2,3)
和(-1,-3),求这个二次函数的表达式.
解:∵该图象经过点(2,3)和(-1,-3),
3=4a+c,
-3=a+c,
∴所求二次函数表达式为
y=2x2-5.
∴{
a=2,
c=-5.
解得
{
76.已知二次函数y=ax2
+
bx的图象经过点(-2,8)
和(-1,5),求这个二次函数的表达式.
解:∵该图象经过点(-2,8)和(-1,5),
8=4a-2b,
5=a-b,
∴{
解得a=-1,b=-6.
∴
y=-x2-6x.
77.已知二次函数的图象经过点(-1,-5),(0,-4)和(1,1).求这个二次函数的表达式.
解:设这个二次函数的表达式为y=ax2+bx+c.
依题意得
∴这个二次函数的表达式为y=2x2+3x-4.
a+b+c=1,
c=-4,
a-b+c=-5,
解得
b=3,
c=-4,
a=2,
78.已知抛物线与x轴相交于点A(-1,0),B(1,0),且过点M(0,1),求此函数的表达式.
解:因为点A(-1,0),B(1,0)是图象与x轴的交点,所以设二次函数的表达式为y=a(x+1)(x-1).
又因为抛物线过点M(0,1),
所以1=a(0+1)(0-1),解得a=-1,
所以所求抛物线的表达式为y=-(x+1)(x-1),
即y=-x2+1.
79.如图,抛物线y=x2+bx+c过点A(-4,-3),与y轴交于点B,对称轴是x=-3,请解答下列问题:
(1)求抛物线的表达式;
解:(1)把点A(-4,-3)代入y=x2+bx+c
得16-4b+c=-3,c-4b=-19.
∵对称轴是x=-3,∴
=-3,
∴b=6,∴c=5,
∴抛物线的表达式是y=x2+6x+5;
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.
(2)∵CD∥x轴,∴点C与点D关于x=-3对称.
∵点C在对称轴左侧,且CD=8,
∴点C的横坐标为-7,
∴点C的纵坐标为(-7)2+6×(-7)+5=12.
∵点B的坐标为(0,5),
∴△BCD中CD边上的高为12-5=7,
∴△BCD的面积=
×8×7=28.
80.
已知二次函数y=a(x-1)2-4的图象经过点(3,0).
(1)求a的值;
(2)若A(m,y1)、B(m+n,y2)(n>0)是该函数图象上的两点,当y1=y
2时,求m、n之间的数量关系.
解:(1)将(3,0)代入y=a(x-1)2-4,
得0=4a-4,解得a=1;
(2)方法一:
根据题意,得y1=(m-1)2-4,y2=(m+n-1)2-4,
∵y1=y2,
∴(m-1)2-4=(m+n-1)2-4,即(m-1)2=(m+n-1)2.
∵n>0,∴m-1=-(m+n-1),化简,得2m+n=2;
方法二:
∵函数y=(x-1)2-4的图象的对称轴是经过点(1,-4),且平行于y轴的直线,
∴m+n-1=1-m,化简,得
2m+n=2.
方法总结:已知函数图象上的点,则这点的坐标必满足函数的表达式,代入即可求得函数解析式.
81.
要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
C(3,0)
B(1,3)
A
x
O
y
1
2
3
1
2
3
解:如图建立直角坐标系,
点(1,3)是图中这段抛物线的顶点.
因此可设这段抛物线对应的函数是
∵这段抛物线经过点(3,0),
∴
0=a(3-1)2+3.
解得:
因此抛物线的解析式为:
y=a(x-1)2+3
(0≤x≤3).
当x=0时,y=2.25.
答:水管长应为2.25m.
3
4
a=-
y=
(x-1)2+3
(0≤x≤3)
3
4
-
O
y
x
–1
–2
3
82.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a、b同号;
(2)当x=–1和x=3时,函数值相等;
(3)
4a+b=0;
(4)当y=–2时,x的值只能取0;
其中正确的是
.
直线x=1
(2)
83.
如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴
×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=±
,
此时P点坐标为(
,2),(-
,2);
当b=-2时,x2-4=-2,解得x=±
,
此时P点坐标为(
,2),(-
,2).
84.
抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2,
,
∴平移后二次函数关系式为y=
(x-3)2.
方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
85:如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴
×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=±
,
此时P点坐标为(
,2),(-
,2);
当b=-2时,x2-4=-2,解得x=±
,
此时P点坐标为(
,2),(-
,2).
86.矩形的周长为16cm,它的一边长为x(cm),面积为y(cm2).求
(1)y与x之间的函数解析式及自变量x的取值范围;
(2)当x=3时矩形的面积.
解:(1)y=(8-x)x=-x2+8x
(0<x<8);
(2)当x=3时,y=-32+8×3=15
cm2
.
87:某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
解:由题意可得
-10x2+180x+400=1120,
整理得
x2-18x+72=0,
解得
x1=6,x2=12(舍去).
所以,该产品的质量档次为第6档.
【方法总结】解决此类问题的关键是要吃透题意,确定变量,建立函数模型.
88.某商店经销一种销售成本为每千克40元的商品,根据市场分析,若按每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量
就减少10kg,针对这种商品的销售情况,请解答下列问题:
(1)当销售单价为每千克55元时,计算月销售量和销售利润分别为多少?
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出自变量x的取值范围)
同课章节目录
