人教版数学五年级下册 6.3分数加减混合运算课件(27张ppt)
文档属性
| 名称 | 人教版数学五年级下册 6.3分数加减混合运算课件(27张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 00:00:00 | ||
图片预览







文档简介
第6单元 分数的加法和减法
分数加减混合运算
一、复习旧知,引入新课
说说下面算式的计算顺序。
32+47-18 95-20+35 42-(21+15)
整数加减混合运算的顺序:加减混合运算是同级运算,运算顺序是从左往右依次计算,有括号的,先算括号里面的。
二、合作交流,探究新知
云梦森林公园地貌情况对比
地貌类型
占公园面积的几分之几
乔木林
灌木林
草地
乔木林和灌木林都属于森林,森林部分比草地部分多几分之几?怎样列式?
提示:分数加减混合运算的顺序和整数
加减混合运算的顺序相同。
这是异分母分数的加减混合运算,得先通分,怎样通分好呢?
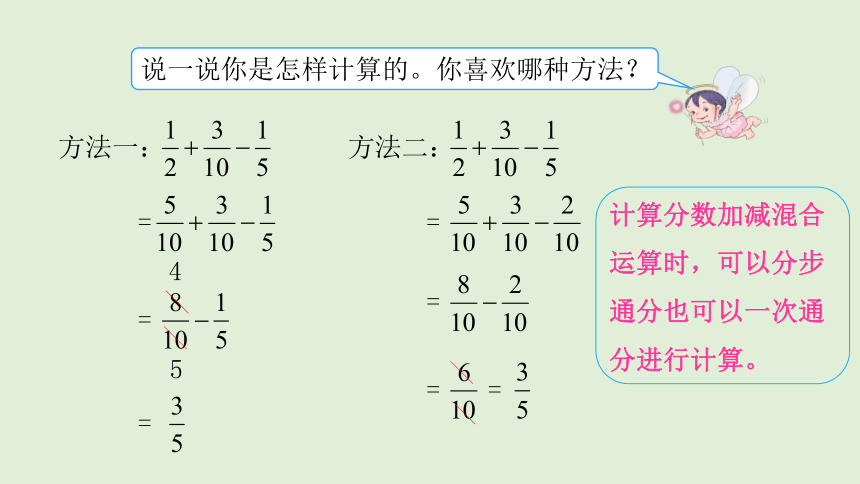
说一说你是怎样计算的。你喜欢哪种方法?
方法一:
=
=
=
方法二:
=
=
=
=
4
5
计算分数加减混合运算时,可以分步通分也可以一次通分进行计算。
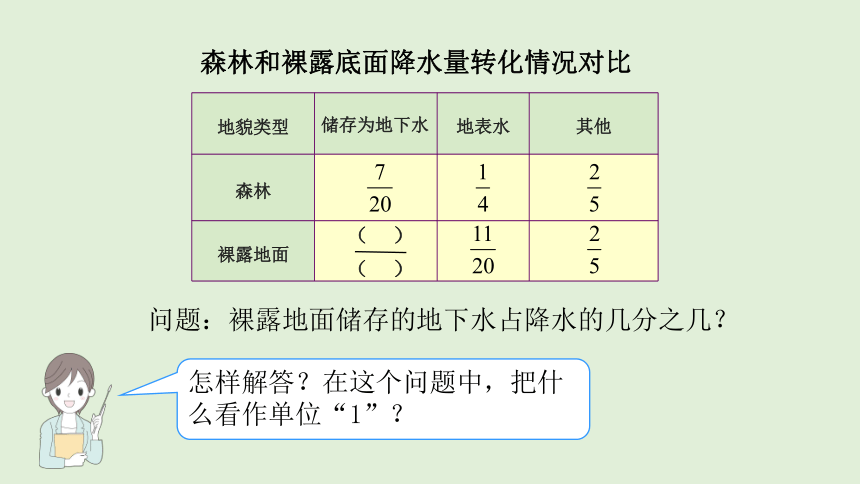
森林和裸露底面降水量转化情况对比
地貌类型
储存为地下水
地表水
其他
森林
裸露地面
( )
( )
怎样解答?在这个问题中,把什么看作单位“1”?
问题:裸露地面储存的地下水占降水的几分之几?
=
=
=
=
=
=
这两种方法有什么不同?
分数加减混合运算与整数加减混合运算的顺序相同,也是按从左往右依次计算,有括号的要先算括号里面的。
(一)基础练习
三、练习巩固,拓展提升
2
3
7
12
1.计算。
5
8
1
5
2
0
7
24
7
12
9
5
总结:学习了分数加减混合运算的运算顺序。知道了分数加减混合运算的运算顺序与整数加减混合运算的运算顺序相同,如果是异分母分数,要先进行通分。计算没有括号的异分母分数加减混合运算时,可以分步通分进行计算,也可以将几个分数一次性通分进行计算。
四、总结归纳
第6单元 分数的加法和减法
分数加减简便运算
一、复习旧知,引入新课
用简便方法计算下面各题。
整数加法交换律:a+b=b+a
整数加法结合律:(a+b)+c=a+(b+c)
53+34+66+47
248+175+252+825
这两题进行简便计算的根据是什么?用字母怎样表示?
当上面各式中的字母表示分数时,加法的交换律和结合律还适用吗?
二、创设情境,探索新知
在加法运算定律中,用字母表示的两个数或三个数,它的适用范围都包括了什么样的数?
……
下面每组算式的左右两边有什么样的关系?
你发现了什么?
=
=
整数加法的交换律、结合律对分数加法同样适用。
利用运算定律可以使一些分数计算变得更简便。
观察这些加数,注意分母和分子有什么特点并讨论怎样可以使计算简便?
8
12
1
应用加法运算定律,可以把分母相同的分数先加起来(或凑成整数),再进行计算。
(一)基础练习
三、练习巩固,拓展提升
1
3
1
1.用简便方法计算下面各题。
1
2
1
1
2
2
2.在 里填上合适的运算符号。
+
+
(二)拓展应用:
3.在括号里填上恰当的数,使等式成立。
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1
4
9
10
5
12
1
4
3
4
总结:通过这节课的学习,我们发现整数加法的交换律、结合律对分数加法同样适用。我们可以从分数的分母中进行辨别,判断出能简算的式子。通过分数加减简便运算,既能提高计算速度,还能提高准确度。
四、总结归纳
第6单元 分数的加法和减法
分数加减混合运算的应用
一、复习旧知,引入新课
这有一张长方形的纸,我把这张纸对折后,用分数怎样表示呢?为什么?
我再将这张纸对折,这时用分数怎样表示呢?再对折呢?同学们发现了什么?
11
12
4
7
20
7
12
二、合作交流,探究新知
一杯纯牛奶,乐乐喝了半杯后,觉得有些凉,就兑满了热水。他又喝了半杯,就出去玩了。乐乐一共喝了多少杯纯牛奶?多少杯水?
提示:喝了几次牛奶?第一次喝了多少?第二次呢?加了多少水?水全喝完了吗?
从题目中能提炼出哪些信息?
第二次喝的纯牛奶比第一次少。
问题是:乐乐一共喝了多少杯纯牛奶?可以用第一次加上第二次来解答。
乐乐一共喝了两次牛奶,第一次喝了 杯,第二次喝了兑水后的 杯。
第二次喝的纯牛奶可能是 杯。
加满水,水是 杯,纯牛奶还是 杯。
第一次喝了 杯纯牛奶
组织研讨:
第一次喝了 杯纯牛奶,第二次喝了多少杯纯牛奶呢?
又喝了 杯,这 杯里,一半是纯牛奶,一半是水
把 杯的纯牛奶再平均分成2份,喝的纯牛奶就是其中的1份了。
}
}
牛奶
水
一共喝的纯牛奶:
(杯)
一共喝的水:
(杯)
(一)基础练习
三、练习巩固,拓展提升
1.五(1)班同学去革命老区参观,共用去10小时。其中路上用去的时间占 ,吃午饭与休息时间共占 ,剩下的是游览的时间,游览的时间占几分之几?
1- - =
1
5
3
10
1
2
答:游览的时间占 。
1
2
总结:这节课我们学习了用分数加减混合运算的应用。在解决实际问题时,必须要先认真审题,理清题目中的各个数量关系,然后进行列式解答。
四、总结归纳
分数加减混合运算
一、复习旧知,引入新课
说说下面算式的计算顺序。
32+47-18 95-20+35 42-(21+15)
整数加减混合运算的顺序:加减混合运算是同级运算,运算顺序是从左往右依次计算,有括号的,先算括号里面的。
二、合作交流,探究新知
云梦森林公园地貌情况对比
地貌类型
占公园面积的几分之几
乔木林
灌木林
草地
乔木林和灌木林都属于森林,森林部分比草地部分多几分之几?怎样列式?
提示:分数加减混合运算的顺序和整数
加减混合运算的顺序相同。
这是异分母分数的加减混合运算,得先通分,怎样通分好呢?
说一说你是怎样计算的。你喜欢哪种方法?
方法一:
=
=
=
方法二:
=
=
=
=
4
5
计算分数加减混合运算时,可以分步通分也可以一次通分进行计算。
森林和裸露底面降水量转化情况对比
地貌类型
储存为地下水
地表水
其他
森林
裸露地面
( )
( )
怎样解答?在这个问题中,把什么看作单位“1”?
问题:裸露地面储存的地下水占降水的几分之几?
=
=
=
=
=
=
这两种方法有什么不同?
分数加减混合运算与整数加减混合运算的顺序相同,也是按从左往右依次计算,有括号的要先算括号里面的。
(一)基础练习
三、练习巩固,拓展提升
2
3
7
12
1.计算。
5
8
1
5
2
0
7
24
7
12
9
5
总结:学习了分数加减混合运算的运算顺序。知道了分数加减混合运算的运算顺序与整数加减混合运算的运算顺序相同,如果是异分母分数,要先进行通分。计算没有括号的异分母分数加减混合运算时,可以分步通分进行计算,也可以将几个分数一次性通分进行计算。
四、总结归纳
第6单元 分数的加法和减法
分数加减简便运算
一、复习旧知,引入新课
用简便方法计算下面各题。
整数加法交换律:a+b=b+a
整数加法结合律:(a+b)+c=a+(b+c)
53+34+66+47
248+175+252+825
这两题进行简便计算的根据是什么?用字母怎样表示?
当上面各式中的字母表示分数时,加法的交换律和结合律还适用吗?
二、创设情境,探索新知
在加法运算定律中,用字母表示的两个数或三个数,它的适用范围都包括了什么样的数?
……
下面每组算式的左右两边有什么样的关系?
你发现了什么?
=
=
整数加法的交换律、结合律对分数加法同样适用。
利用运算定律可以使一些分数计算变得更简便。
观察这些加数,注意分母和分子有什么特点并讨论怎样可以使计算简便?
8
12
1
应用加法运算定律,可以把分母相同的分数先加起来(或凑成整数),再进行计算。
(一)基础练习
三、练习巩固,拓展提升
1
3
1
1.用简便方法计算下面各题。
1
2
1
1
2
2
2.在 里填上合适的运算符号。
+
+
(二)拓展应用:
3.在括号里填上恰当的数,使等式成立。
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1
4
9
10
5
12
1
4
3
4
总结:通过这节课的学习,我们发现整数加法的交换律、结合律对分数加法同样适用。我们可以从分数的分母中进行辨别,判断出能简算的式子。通过分数加减简便运算,既能提高计算速度,还能提高准确度。
四、总结归纳
第6单元 分数的加法和减法
分数加减混合运算的应用
一、复习旧知,引入新课
这有一张长方形的纸,我把这张纸对折后,用分数怎样表示呢?为什么?
我再将这张纸对折,这时用分数怎样表示呢?再对折呢?同学们发现了什么?
11
12
4
7
20
7
12
二、合作交流,探究新知
一杯纯牛奶,乐乐喝了半杯后,觉得有些凉,就兑满了热水。他又喝了半杯,就出去玩了。乐乐一共喝了多少杯纯牛奶?多少杯水?
提示:喝了几次牛奶?第一次喝了多少?第二次呢?加了多少水?水全喝完了吗?
从题目中能提炼出哪些信息?
第二次喝的纯牛奶比第一次少。
问题是:乐乐一共喝了多少杯纯牛奶?可以用第一次加上第二次来解答。
乐乐一共喝了两次牛奶,第一次喝了 杯,第二次喝了兑水后的 杯。
第二次喝的纯牛奶可能是 杯。
加满水,水是 杯,纯牛奶还是 杯。
第一次喝了 杯纯牛奶
组织研讨:
第一次喝了 杯纯牛奶,第二次喝了多少杯纯牛奶呢?
又喝了 杯,这 杯里,一半是纯牛奶,一半是水
把 杯的纯牛奶再平均分成2份,喝的纯牛奶就是其中的1份了。
}
}
牛奶
水
一共喝的纯牛奶:
(杯)
一共喝的水:
(杯)
(一)基础练习
三、练习巩固,拓展提升
1.五(1)班同学去革命老区参观,共用去10小时。其中路上用去的时间占 ,吃午饭与休息时间共占 ,剩下的是游览的时间,游览的时间占几分之几?
1- - =
1
5
3
10
1
2
答:游览的时间占 。
1
2
总结:这节课我们学习了用分数加减混合运算的应用。在解决实际问题时,必须要先认真审题,理清题目中的各个数量关系,然后进行列式解答。
四、总结归纳
