初中数学人教版八年级下学期专题复习:05 菱形(含解析)
文档属性
| 名称 | 初中数学人教版八年级下学期专题复习:05 菱形(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 11:18:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学人教版八年级下学期专题复习 :05 菱形
一、单选题
1.矩形具有而菱形不具有的性质是(?? )
A.?对角相等???????????????????????B.?对角线互相垂直???????????????????????C.?对角线相等???????????????????????D.?对边平行
2.已知四边形ABCD是平行四边形,则下列结论中正确的是(?? )
A.?当AB⊥BD时,它是菱形?????????????????????????????????????B.?当AC=BD时,它是正方形
C.?当∠ABC=90°时,它是矩形????????????????????????????????D.?当AB=BC时,它是矩形21*cnjy*com
3.如图,菱形ABCD的两条对角线长分别为AC=6,BD=8,点P是BC边上的一动点,则AP的最小值为(? ) 【来源:21cnj*y.co*m】
A.?4??????????????????????????????????????????B.?4.8??????????????????????????????????????????C.?5??????????????????????????????????????????D.?5.5
4.如图,菱形 中, ,则 的度数为(?? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
5.如图,在菱形ABCD中, , ,则 的周长等于(?? )
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?12
6.已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为(??? )
A.?4??????????????????????????????????????????B.???????????????????????????????????????????C.?2??????????????????????????????????????????D.?1
二、填空题
7.如图,在四边形 中,对角线 交于点 ,且 ,若要使四边形 是菱形,则可以添加的条件是________. 【来源:21·世纪·教育·网】
8.如图,AC是菱形ABC_D??????è§???????_P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2 , 则PE+PF的值是________cm.
9.如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是________.
10.如图,菱形ABCD的边长_???13??????è§?_线AC=24,点E、F分别是边CD、BC的中点,连接EF 并延长与AB的延长线相交于点G,则EG = ________. 21世纪教育网版权所有
三、综合题
11.如图,已知四边形 是平行四边形,E是 延长线上一点且 ,连接 , .
(1)求证:四边形 是平行四边形
(2)连接 ,若 , ,求 的面积.
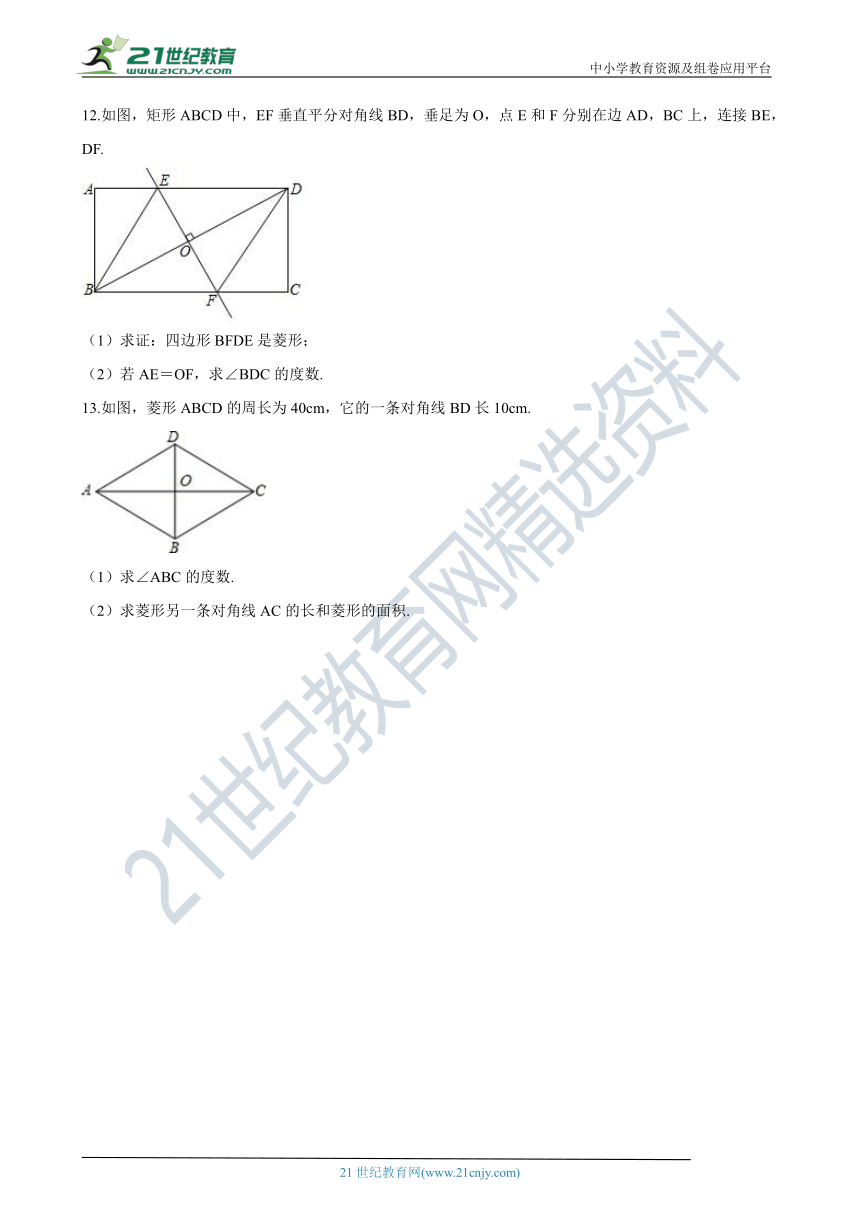
12.如图,矩形ABCD中,EF垂直平分对角线BD,垂足为O,点E和F分别在边AD,BC上,连接BE,DF. 【出处:21教育名师】
(1)求证:四边形BFDE是菱形;
(2)若AE=OF,求∠BDC的度数.
13.如图,菱形ABCD的周长为40cm,它的一条对角线BD长10cm.
(1)求∠ABC的度数.
(2)求菱形另一条对角线AC的长和菱形的面积.
答案解析部分
一、单选题
1.答案: C
解析:解:矩形的对角线相等,对边平行且相等,对角也相等,
菱形的对角相等,对角线互相垂直平分,对边平行且相等,
于是可得矩形具有菱形不具有的性质是对角线相等,
故答案为:C.
分析:根据矩形、菱形的性质逐项判定即可。
2.答案: C
解析:解_???A????????A_C⊥BD时,四边形ABCD是菱形,故A错误;
B、当AC=BD时,四边形ABCD是矩形,故B错误;
C、当∠ABC=90°时,四边形ABCD是矩形,故C正确;
D、 当AB=BC时,四边形ABCD是菱形,故D错误.
故答案为:C.
分析:对角线互相垂直的平行四边形是菱形,邻边相等的平行四边形是菱形,对角线相等的平行四边形是矩形,有一个角是90°的平行四边形是矩形.【版权所有:21教育】
3.答案: B
解析:如图,设AC与BD的交点为O,
∵点P是BC边上的一动点,
∴AP⊥BC时,AP有最小值,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO= AC=3,BO=DO= BD=4,
∴BC= ,
∵S菱形ABCD= ×AC×BD=BC×AP,
∴AP= =4.8,
故答案为:B.
分析:设AC与B_D?????¤??????O_,利用垂线段最短,可知当AP⊥BC时,AP的值最小,再利用菱形的性质可求出BO,CO的长,利用勾股定理求出BC的长;然后利用菱形的两个面积公式求出AP的长.
4.答案: A
解析:解:∵四边形ABCD为菱形,∴AD=AB,
∴∠ADB=∠ABD=(180°-∠A)÷2=(180°-50°)÷2=65°,
故答案为:A.
分析:由菱形的性质可得AD=AB,于是根据等边对等角可得∠ADB=∠ABD,然后由三角形内角和定理可求解.21cnjy.com
5.答案: B
解析:解:在菱形ABCD中,AB∥CD,
∵∠BCD=120°,
∴∠B=60°,
∵BA=BC,
∴△ABC是等边三角形,
故可得△ABC的周长=3AB=15.
故答案为:B.
分析:根据题意可得出∠B=60°,结合菱形的性质可得BA=BC,判断出△ABC是等边三角形即可得出△ABC的周长.www.21-cn-jy.com
6.答案: C
解析:如图,由题意得:菱形ABCD的周长为8, ,
,
是等边三角形,
,
,
该菱形较短的对角线长为 ,
故答案为:C.
分析:先画出图形,再根据菱形的性质、等边三角形的判定与性质即可得.
二、填空题
7.答案:
解析:
???????
四边形 是平行四边形,
邻边相等的平行四边形是菱形,
添加的条件是 (答案不唯一),
故答案为:
分析:根据菱形的判定方法求解即可。
8.答案: 2
解析:解:连接BP,
∵ 四边形ABCD是菱形,且周长是12cm,面积是6cm2
∴AB=BC= ×12=3(cm),
∵AC是菱形ABCD的对角线,
∴ S△ABC=S△ABP+S△BPC= =3(cm2),
∴S△ABP+S△BPC= AB?PE+ BC?PE=3(cm2),
∴ ×3×PE+ ×3×PF=3,
∴PE+PF=3× =2(cm),
故答案为:2.
分析:连接BP,根据菱形性质和三角形的面积公式得S△ABC=S△ABP+S△BPC= ,S△ABP+S△BPC= AB?PE+ BC?PE把相应的值代入即可.21教育网
9.答案:
解析:解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC= AC= ×4=2,∠BAC= ∠BAD= ×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB= ,
∴BD=2OB= ,
∴该菱形的面积是: AC?BD= ×4× = ,
故答案为: .
分析:首先由四边形ABCD是菱形,求得AC⊥BD,OA= AC,∠BAC= ∠BAD,然后在直角三角形AOB中,利用30°角所对的直角边等于斜边的一半与勾股定理即可求得OB的长,然后由菱形的面积等于其对角线积的一半,即可求得该菱形的面积.21·cn·jy·com
10.答案: 10
解析:解:连接BD交AC与点O,
在菱形ABCD中
∵ ,
在 中
,
∴ ,
∵点E、F分别是边CD、BC的中点,
∴ ,
∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ .
故答案为:10.
分析:连接BD交AC与点O,证明四边形BDEG是平行四边形,得EG=BD,利用勾股定理求出OD的长,BD=2OD,即可求出EG。www-2-1-cnjy-com
三、综合题
11.答案: (1)解:∵四边形 是平行四边形,
∴ , ,
又∵ ,
∴ , ,
∴四边形 是平行四边形.
(2)解:如图,连接 ,交 于点O,
∵ , ,
∴ ,由(1)得四边形 是平行四边形,
∴ 是菱形,
∴ ,
∵ ,
∴ ,
在 中, ,
∴ ,
∴ .
分析:(1)利用平行四_è??????????§è?¨???_证得AB=CD,AB∥CD,再由已知可推出BE=CD;然后利用有一组对边平行且相等的四边形是平行四边形,可证得结论.
(2)连接DE交BC于点O,利用已知条件易证BD=BE,利用有一组邻边相等的平行四边形是菱形,可推出四边形BECD是菱形,利用菱形的对角线互相垂直,可得到DE⊥BC,同时可求出OE的长;在Rt△BOE中,利用勾股定理求出BO的长,从而可得到BC的长;然后利用菱形的面积等于两对角线之积的一半,可求出菱形BECD的面积.2·1·c·n·j·y
12.答案: (1)证明:∵四边形ABCD是矩形,
∴ AD∥BC,AD=BC,
∴∠EDO=∠OBF,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=90°,
∴△DEO≌△BFO(ASA)
∴OE=OF,
∴四边形EBFD是平行四边形,
又EF⊥BD,
∴四边形EBFD是菱形;
(2)解: ∵四边形EBFD是菱形,
∴BF=EB
又 AE=OF,∠A=∠BOF
∴△ABE≌△OBF
∴∠ABE=∠OBF,
∵∠FBO=∠OBE,
∴∠ABE =∠FBO=∠OBE,
∴ ∠OBF=30°
∴∠BDC=60°.
分析:(1)_é???????¤??????è??_形EBFD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形进行判定即可;
(2)由四边形BFDE是菱形得BE=BF,可证△ABE≌△OBF,∠ABE=∠OBF,∠FBO=∠OBF,∠OBF=30°,即可求解.21·世纪*教育网
13.答案: (1)解:∵菱形周长为40cm,
∴AB=BC=CD=AD=10cm,AD//BC
∵DB=10cm,
∴△ABD为等边三角形,
∴∠BAD=60°,
∴∠ABC=180°-60°=120°
(2)解:在菱形ABCD中,AC⊥BD
在Rt△ABO中,AB=10cm,BO= ×10cm=5cm,
∴
∴AC=2AO=
∴菱形面积S= ×AC×BD= ×10× =
分析:(1)根据菱形的_??§è?¨??????_A_B=BC=CD=AD=10cm,AD//BC,再根据DB=10cm,得出△ABD为等边三角形,得出∠BAD=60°,即可得出∠ABC=120°;
(2)根据勾股定理求出AO的长,从而求出AC的长,再根据菱形的面积公式进行计算,即可求出菱形的面积.
?
_21?????????è?????(www.21cnjy.com)_
初中数学人教版八年级下学期专题复习 :05 菱形
一、单选题
1.矩形具有而菱形不具有的性质是(?? )
A.?对角相等???????????????????????B.?对角线互相垂直???????????????????????C.?对角线相等???????????????????????D.?对边平行
2.已知四边形ABCD是平行四边形,则下列结论中正确的是(?? )
A.?当AB⊥BD时,它是菱形?????????????????????????????????????B.?当AC=BD时,它是正方形
C.?当∠ABC=90°时,它是矩形????????????????????????????????D.?当AB=BC时,它是矩形21*cnjy*com
3.如图,菱形ABCD的两条对角线长分别为AC=6,BD=8,点P是BC边上的一动点,则AP的最小值为(? ) 【来源:21cnj*y.co*m】
A.?4??????????????????????????????????????????B.?4.8??????????????????????????????????????????C.?5??????????????????????????????????????????D.?5.5
4.如图,菱形 中, ,则 的度数为(?? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
5.如图,在菱形ABCD中, , ,则 的周长等于(?? )
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?12
6.已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为(??? )
A.?4??????????????????????????????????????????B.???????????????????????????????????????????C.?2??????????????????????????????????????????D.?1
二、填空题
7.如图,在四边形 中,对角线 交于点 ,且 ,若要使四边形 是菱形,则可以添加的条件是________. 【来源:21·世纪·教育·网】
8.如图,AC是菱形ABC_D??????è§???????_P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2 , 则PE+PF的值是________cm.
9.如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是________.
10.如图,菱形ABCD的边长_???13??????è§?_线AC=24,点E、F分别是边CD、BC的中点,连接EF 并延长与AB的延长线相交于点G,则EG = ________. 21世纪教育网版权所有
三、综合题
11.如图,已知四边形 是平行四边形,E是 延长线上一点且 ,连接 , .
(1)求证:四边形 是平行四边形
(2)连接 ,若 , ,求 的面积.
12.如图,矩形ABCD中,EF垂直平分对角线BD,垂足为O,点E和F分别在边AD,BC上,连接BE,DF. 【出处:21教育名师】
(1)求证:四边形BFDE是菱形;
(2)若AE=OF,求∠BDC的度数.
13.如图,菱形ABCD的周长为40cm,它的一条对角线BD长10cm.
(1)求∠ABC的度数.
(2)求菱形另一条对角线AC的长和菱形的面积.
答案解析部分
一、单选题
1.答案: C
解析:解:矩形的对角线相等,对边平行且相等,对角也相等,
菱形的对角相等,对角线互相垂直平分,对边平行且相等,
于是可得矩形具有菱形不具有的性质是对角线相等,
故答案为:C.
分析:根据矩形、菱形的性质逐项判定即可。
2.答案: C
解析:解_???A????????A_C⊥BD时,四边形ABCD是菱形,故A错误;
B、当AC=BD时,四边形ABCD是矩形,故B错误;
C、当∠ABC=90°时,四边形ABCD是矩形,故C正确;
D、 当AB=BC时,四边形ABCD是菱形,故D错误.
故答案为:C.
分析:对角线互相垂直的平行四边形是菱形,邻边相等的平行四边形是菱形,对角线相等的平行四边形是矩形,有一个角是90°的平行四边形是矩形.【版权所有:21教育】
3.答案: B
解析:如图,设AC与BD的交点为O,
∵点P是BC边上的一动点,
∴AP⊥BC时,AP有最小值,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO= AC=3,BO=DO= BD=4,
∴BC= ,
∵S菱形ABCD= ×AC×BD=BC×AP,
∴AP= =4.8,
故答案为:B.
分析:设AC与B_D?????¤??????O_,利用垂线段最短,可知当AP⊥BC时,AP的值最小,再利用菱形的性质可求出BO,CO的长,利用勾股定理求出BC的长;然后利用菱形的两个面积公式求出AP的长.
4.答案: A
解析:解:∵四边形ABCD为菱形,∴AD=AB,
∴∠ADB=∠ABD=(180°-∠A)÷2=(180°-50°)÷2=65°,
故答案为:A.
分析:由菱形的性质可得AD=AB,于是根据等边对等角可得∠ADB=∠ABD,然后由三角形内角和定理可求解.21cnjy.com
5.答案: B
解析:解:在菱形ABCD中,AB∥CD,
∵∠BCD=120°,
∴∠B=60°,
∵BA=BC,
∴△ABC是等边三角形,
故可得△ABC的周长=3AB=15.
故答案为:B.
分析:根据题意可得出∠B=60°,结合菱形的性质可得BA=BC,判断出△ABC是等边三角形即可得出△ABC的周长.www.21-cn-jy.com
6.答案: C
解析:如图,由题意得:菱形ABCD的周长为8, ,
,
是等边三角形,
,
,
该菱形较短的对角线长为 ,
故答案为:C.
分析:先画出图形,再根据菱形的性质、等边三角形的判定与性质即可得.
二、填空题
7.答案:
解析:
???????
四边形 是平行四边形,
邻边相等的平行四边形是菱形,
添加的条件是 (答案不唯一),
故答案为:
分析:根据菱形的判定方法求解即可。
8.答案: 2
解析:解:连接BP,
∵ 四边形ABCD是菱形,且周长是12cm,面积是6cm2
∴AB=BC= ×12=3(cm),
∵AC是菱形ABCD的对角线,
∴ S△ABC=S△ABP+S△BPC= =3(cm2),
∴S△ABP+S△BPC= AB?PE+ BC?PE=3(cm2),
∴ ×3×PE+ ×3×PF=3,
∴PE+PF=3× =2(cm),
故答案为:2.
分析:连接BP,根据菱形性质和三角形的面积公式得S△ABC=S△ABP+S△BPC= ,S△ABP+S△BPC= AB?PE+ BC?PE把相应的值代入即可.21教育网
9.答案:
解析:解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC= AC= ×4=2,∠BAC= ∠BAD= ×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB= ,
∴BD=2OB= ,
∴该菱形的面积是: AC?BD= ×4× = ,
故答案为: .
分析:首先由四边形ABCD是菱形,求得AC⊥BD,OA= AC,∠BAC= ∠BAD,然后在直角三角形AOB中,利用30°角所对的直角边等于斜边的一半与勾股定理即可求得OB的长,然后由菱形的面积等于其对角线积的一半,即可求得该菱形的面积.21·cn·jy·com
10.答案: 10
解析:解:连接BD交AC与点O,
在菱形ABCD中
∵ ,
在 中
,
∴ ,
∵点E、F分别是边CD、BC的中点,
∴ ,
∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ .
故答案为:10.
分析:连接BD交AC与点O,证明四边形BDEG是平行四边形,得EG=BD,利用勾股定理求出OD的长,BD=2OD,即可求出EG。www-2-1-cnjy-com
三、综合题
11.答案: (1)解:∵四边形 是平行四边形,
∴ , ,
又∵ ,
∴ , ,
∴四边形 是平行四边形.
(2)解:如图,连接 ,交 于点O,
∵ , ,
∴ ,由(1)得四边形 是平行四边形,
∴ 是菱形,
∴ ,
∵ ,
∴ ,
在 中, ,
∴ ,
∴ .
分析:(1)利用平行四_è??????????§è?¨???_证得AB=CD,AB∥CD,再由已知可推出BE=CD;然后利用有一组对边平行且相等的四边形是平行四边形,可证得结论.
(2)连接DE交BC于点O,利用已知条件易证BD=BE,利用有一组邻边相等的平行四边形是菱形,可推出四边形BECD是菱形,利用菱形的对角线互相垂直,可得到DE⊥BC,同时可求出OE的长;在Rt△BOE中,利用勾股定理求出BO的长,从而可得到BC的长;然后利用菱形的面积等于两对角线之积的一半,可求出菱形BECD的面积.2·1·c·n·j·y
12.答案: (1)证明:∵四边形ABCD是矩形,
∴ AD∥BC,AD=BC,
∴∠EDO=∠OBF,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=90°,
∴△DEO≌△BFO(ASA)
∴OE=OF,
∴四边形EBFD是平行四边形,
又EF⊥BD,
∴四边形EBFD是菱形;
(2)解: ∵四边形EBFD是菱形,
∴BF=EB
又 AE=OF,∠A=∠BOF
∴△ABE≌△OBF
∴∠ABE=∠OBF,
∵∠FBO=∠OBE,
∴∠ABE =∠FBO=∠OBE,
∴ ∠OBF=30°
∴∠BDC=60°.
分析:(1)_é???????¤??????è??_形EBFD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形进行判定即可;
(2)由四边形BFDE是菱形得BE=BF,可证△ABE≌△OBF,∠ABE=∠OBF,∠FBO=∠OBF,∠OBF=30°,即可求解.21·世纪*教育网
13.答案: (1)解:∵菱形周长为40cm,
∴AB=BC=CD=AD=10cm,AD//BC
∵DB=10cm,
∴△ABD为等边三角形,
∴∠BAD=60°,
∴∠ABC=180°-60°=120°
(2)解:在菱形ABCD中,AC⊥BD
在Rt△ABO中,AB=10cm,BO= ×10cm=5cm,
∴
∴AC=2AO=
∴菱形面积S= ×AC×BD= ×10× =
分析:(1)根据菱形的_??§è?¨??????_A_B=BC=CD=AD=10cm,AD//BC,再根据DB=10cm,得出△ABD为等边三角形,得出∠BAD=60°,即可得出∠ABC=120°;
(2)根据勾股定理求出AO的长,从而求出AC的长,再根据菱形的面积公式进行计算,即可求出菱形的面积.
?
_21?????????è?????(www.21cnjy.com)_
