第四章 三角形单元检测题1(含答案)
文档属性
| 名称 | 第四章 三角形单元检测题1(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 432.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 12:47:19 | ||
图片预览


文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2020?2021学年度下学期七年级数学(下册)
第四章三角形检测题1
(有答案)
(时间:120分钟
满分:120分)
一、选择题
(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1、下列各组数中,不可能成为一个三角形三边长的是( )
A.3,4,5
B.1,1,1
C.5,7,12
D.5,12,15
2、如图,AC⊥BC,CD⊥AB,DE⊥AC,垂足分别为C,D,E,则下列说法不正确的是( )
A.CD是△ABC的高
B.DE是△ACD的高
C.CE是△CDE的高
D.BD是△CDE的高
3、下列说法不正确的是( )
A.全等三角形的大小、形状相同
B.全等三角形的面积相等
C.全等三角形的周长相等
D.周长相等的三角形是全等三角形
4、如图在△ABC中,已知点D、E、F分别为边BC,AB,AC的中点,且△ABC的面积是12,则阴影部分的面积是(
)
A.2
B.4
C.6
D.8
5、已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序依次为( )
①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.
A.③①②
B.①②③
C.②③①
D.③②①
6、如图,点A,D在线段BC的同一侧,AC与BD相交于点E,连接AB,CD,已知∠1=∠2,现添加以下哪个条件仍不能判定△ABC≌△DCB的是
(????
)
A.∠A=∠D?
???
???
B.AC=DB
C.∠ABC=∠DCB?
???????
D.AB=DC
7、如图,如果AD∥BC,AD=BC,AC与BD相交于O点,则图中的全等三角形一共有( )
A.2对
B.3对
C.4对
D.5对
8、如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=38°,∠C=50°,
则∠EAD
=(
)
A.20°
B.15°
C.12°
D.6°
9、如图,三角形纸片ABC中,将∠C沿DE折叠,使点A落在△ABC外部点处,若∠1=20°,则∠1,∠2,∠A的等量关系为(
)
A.∠1+∠2=∠A
B.∠1?∠2=2∠A
C.∠1+∠2=2∠A
D.∠2?∠1=∠A
10、如图,在△ABC中,AD为BC边上的中线,若AB=4,AC=2,则AD的取值范围是(
)
A.1????
B.2C.2??????
??
D.2二、填空题
(每题3分,共30分)
11、在△ABC中,∠A=∠B=∠C,则此三角形是
三角形(填“直角”或“锐角”或“钝角”).
12、如图所示,要测量池塘两岸相对的两点A,B之间的距离,可先在平地上取一个可以直接到达点A和B的点O,连接AO并延长到点D,使DO=OA,连接BO并延长到C,使CO=BO,连接CD,出CD=akm,则AB两点间的距离为
.
13、如图在四边形ABCD中,若沿着直线EF剪去一个50°的解得到一个五边形,则∠1+∠2=
.
14、已知在△ABC中,第二条边的长是第一条边的3倍多3cm,第三条边的长是第二条边的2倍少17cm,若这个三角形的周长为59cm,则此三角形的三边分别为
cm,
cm,
cm.
15、如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是
.
16、如图,若△ABC是等腰三角形,a,b是其两边,且满足,则△ABC周长为
.
17、在直角三角形中,一个锐角∠A是另一个锐角∠B的3倍,则∠B度数是
.
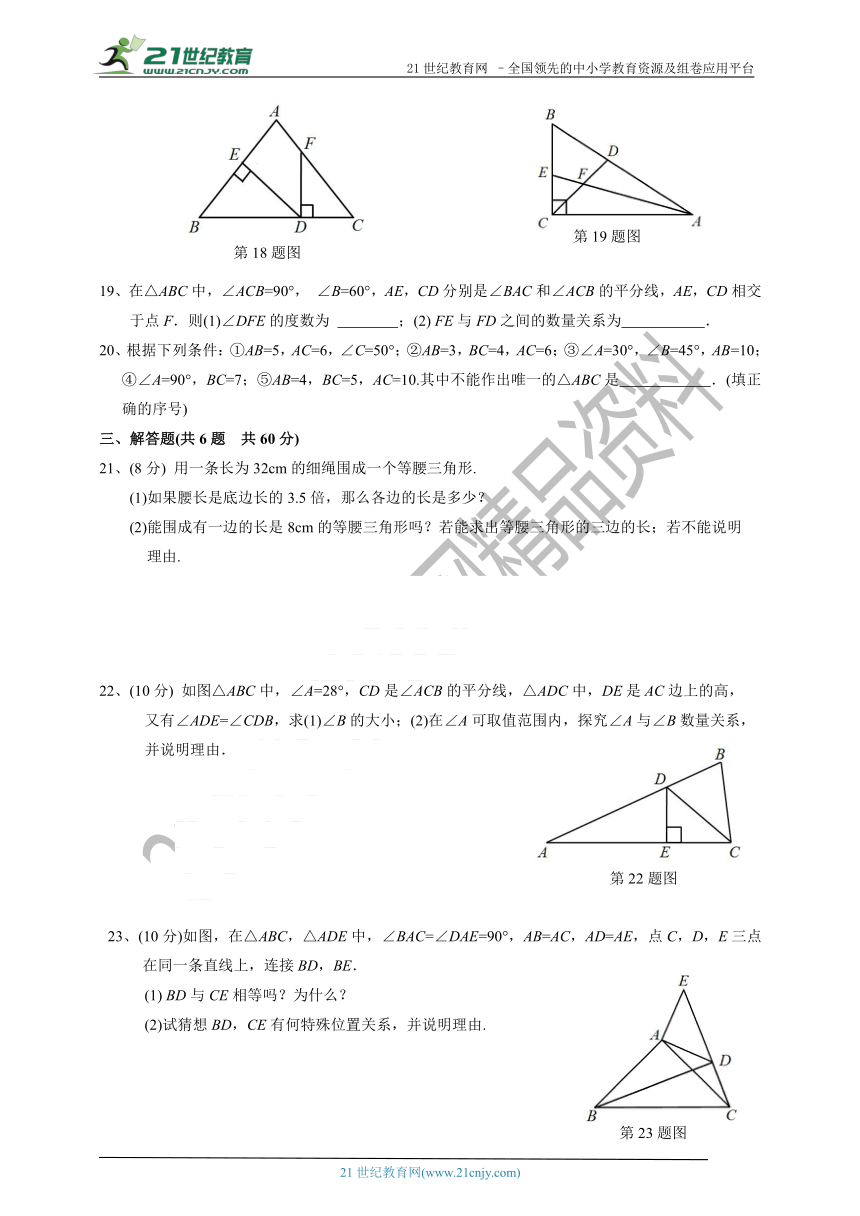
18、如图,在△ABC中,∠B=∠C,点D在BC上DE⊥AB于点E,FD⊥BC交AC与点F.若∠AFD=142°,则∠EDF=
.
19、在△ABC中,∠ACB=90°,
∠B=60°,AE,CD分别是∠BAC和∠ACB的平分线,AE,CD相交于点F.则(1)∠DFE的度数为
;(2)
FE与FD之间的数量关系为
.
20、根据下列条件:①AB=5,AC=6,∠C=50°;②AB=3,BC=4,AC=6;③∠A=30°,∠B=45°,AB=10;④∠A=90°,BC=7;⑤AB=4,BC=5,AC=10.其中不能作出唯一的△ABC是
.(填正确的序号)
三、解答题(共6题
共60分)
21、(8分)
用一条长为32cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3.5倍,那么各边的长是多少?
(2)能围成有一边的长是8cm的等腰三角形吗?若能求出等腰三角形的三边的长;若不能说明
理由.
22、(10分)
如图△ABC中,∠A=28°,CD是∠ACB的平分线,△ADC中,DE是AC边上的高,
又有∠ADE=∠CDB,求(1)∠B的大小;(2)在∠A可取值范围内,探究∠A与∠B数量关系,
并说明理由.
23、(10分)如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.
(1)
BD与CE相等吗?为什么?
(2)试猜想BD,CE有何特殊位置关系,并说明理由.
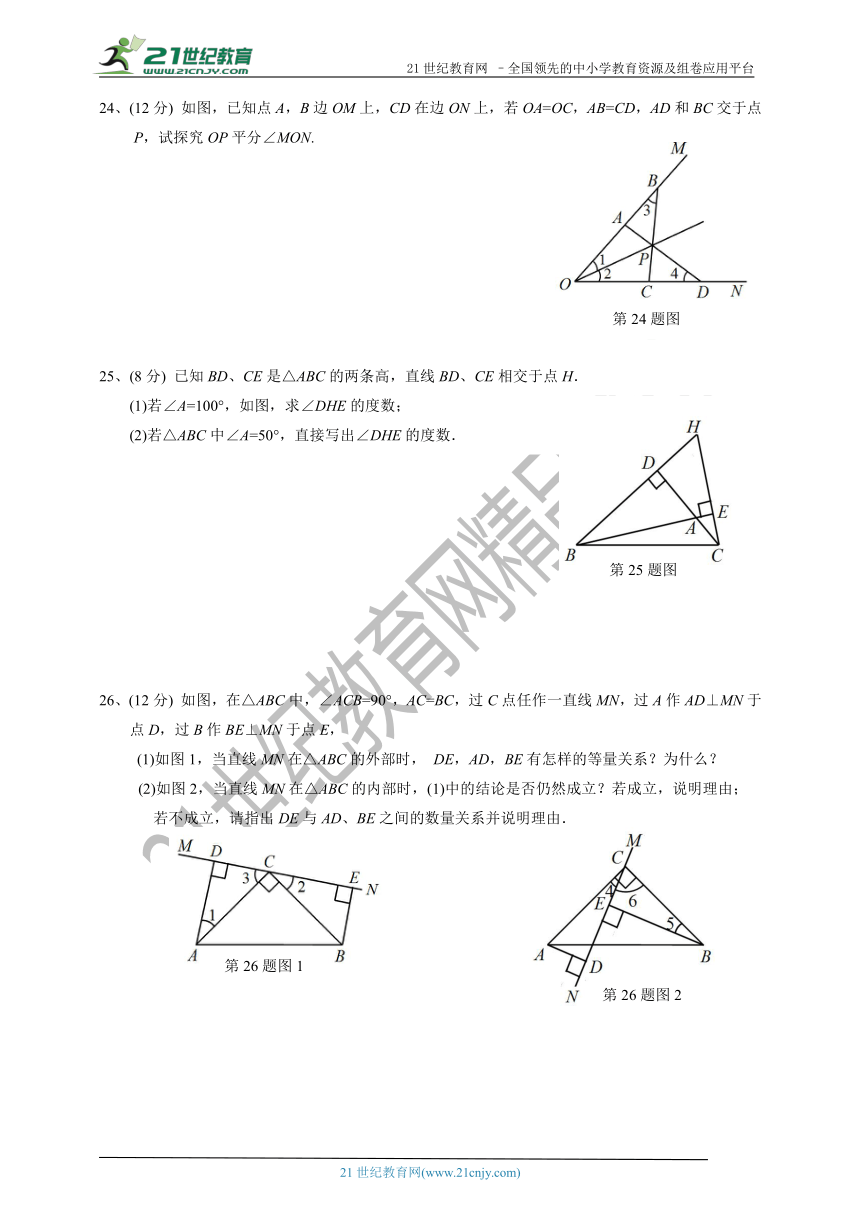
24、(12分)
如图,已知点A,B边OM上,CD在边ON上,若OA=OC,AB=CD,AD和BC交于点P,试探究OP平分∠MON.
25、(8分)
已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)若∠A=100°,如图,求∠DHE的度数;
(2)若△ABC中∠A=50°,直接写出∠DHE的度数.
26、(12分)
如图,在△ABC中,∠ACB=90°,AC=BC,过C点任作一直线MN,过A作AD⊥MN于点D,过B作BE⊥MN于点E,
(1)如图1,当直线MN在△ABC的外部时,
DE,AD,BE有怎样的等量关系?为什么?
(2)如图2,当直线MN在△ABC的内部时,(1)中的结论是否仍然成立?若成立,说明理由;
若不成立,请指出DE与AD、BE之间的数量关系并说明理由.
参考答案
一、选择题(共10小题
每3分
共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
D
B
A
D
C
D
B
A
二、填空题(共10小题
每题3分
共30分)
11、直角三角形
12、akm
13、230°
14、7,23,29
15、108
16、20
17、
22.5°
18、52°
19、120°,FE=FD
20、①②④
三、解答题(共6题
共60分)
21、(8分)
用一条长为32cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3.5倍,那么各边的长是多少?
(2)能围成有一边的长是8cm的等腰三角形吗?若能求出等腰三角形的三边的长;若不能说明
理由.
解:(1)设底边长为xcm,则腰长为3.5xcm,则
3.5x+3.5x+x=32
解得,x=4,
∴3.5x=14,
∴各边长为:14cm,14cm,4cm.
(2)①当8cm为底时,腰长=12cm;
②当8cm为腰时,底边=16cm,因为8+8=16,故不能构成三角形,
所以能构成底边为8cm,腰长为12cm的等腰三角形.
22、(10分)
如图△ABC中,∠A=28°,CD是∠ACB的平分线,△ADC中,DE是AC边上的高,
又有∠ADE=∠CDB,求(1)∠B的大小;(2)在∠A可取值范围内,探究∠A与∠B数量关系,
并说明理由.
解:(1)∵DE是AC边上的高,
∴∠AED=∠DEC=90°,
∵∠A=28°,
∴∠ADE=90°?28°=62°,
∵∠ADE=∠CDB,
∴∠CDE=180°?62°×2=56°,
在Rt△CDE中,∠DCE=90°?56°=34°,
∵CD是∠ACB的平分线,
∴∠ACB=2∠DCE=2×34°=68°,
在△ABC中,∠B=180°?∠ACB?∠A=180°?68°?28°=84°.
(2)∠B=3∠A,理由如下:
根据(1)可得,∠ADE=90°?∠A,
∠CDB
=∠ADE
=90°?∠A,
∴∠CDE=180°?∠CDB
?∠ADE=180°?
2×(90°?∠A)=
2∠A,
在Rt△CDE中,∠DCE=90°?
2∠A,
∵CD是∠ACB的平分线,
∴∠ACB=2∠DCE=2×(90°?
2∠A)
=180°?4∠A,
在△ABC中,∠B=180°?∠ACB?∠A=180°?(180°?4∠A)
?∠A
=3∠A.
23、(10分)如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.
(1)
BD与CE相等吗?为什么?
(2)试猜想BD,CE有何特殊位置关系,并说明理由.
解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,
∵,
∴△BAD≌△CAE(SAS),
∴BD=CE;
②∵△BAD≌△CAE,
∴∠1=∠2,
∵∠AGB=∠CGD,∠BAC
=90°,
∴∠CDG=90°,
∴BD⊥CE.
24、(12分)
如图,已知点A,B边OM上,CD在边ON上,若OA=OC,AB=CD,AD和BC交于点P,试探究OP平分∠MON.
解:∵OA=OC,AB=CD,
∴OA+AB=OC+CD
即OB=OD,
在△OAD和△OCB中,
∵,
∴△OAD≌△OCB(SAS),
∴∠3=∠4,
∵∠BAP=∠AOC+∠4,∠DCP=∠COA+∠3
∴∠BAP=∠DCP
,
在△ABP和△CDP中,
∵,
∴△ABP≌△CDP(ASA),
∴PB=PD,
在△OBP和△ODP中,
∵,
∴△OBP≌△ODP(SSS),
∴∠1=∠2.
∴OP平分∠MON.
25、(8分)
已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)若∠A=100°,如图,求∠DHE的度数;
(2)若△ABC中∠A=50°,直接写出∠DHE的度数.
解:(1)∵BD、CE是△ABC的两条高,
∴∠HDA=∠HEA=90°,
∴∠DHE=180°?∠A=80°;
(2)当∠A=50°时,
①△ABC是锐角三角形时,∠DHE=180°?50°=130°;
②△ABC是钝角三角形时,∠DHE=∠A=50°;
故答案为:50°或130°.
26、(12分)
如图,在△ABC中,∠ACB=90°,AC=BC,过C点任作一直线MN,过A作AD⊥MN于点D,过B作BE⊥MN于点E,
(1)如图1,当直线MN在△ABC的外部时,
DE,AD,BE有怎样的等量关系?为什么?
(2)如图2,当直线MN在△ABC的内部时,(1)中的结论是否仍然成立?若成立,说明理由;若不成立,请指出DE与AD、BE之间的数量关系并说明理由.
(1)解:DE=AD+BE.理由如下:
∵AD⊥MN于D,
BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠1+∠3=90°,
∵∠ACB=90°,
∴∠2+∠3=90°,
∴∠1=∠2,
在△ACD和△CBE中,
∵,
∴△ACD≌△CBE(AAS),
∴AD=CE,DC=EB,
∴DE=DC+CE=AD+BE;
(2)(1)中的结论不成立,DE与AD、BE之间的数量关系为DE=BE?AD.理由如下:
∵AD⊥MN于D,
BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠5+∠6=90°,
∵∠ACB=90°,
∴∠4+∠6=90°,
∴∠4=∠5,
在△ACD和△CBE中,
∵,
∴△ACD≌△CBE(AAS),
∴AD=CE,DC=EB,
∴DE=DC?CE=BE?AD.
第8题图
第23题图
第24题图
第6题图
第26题图2
第25题图
第12题图
第26题图2
第22题图
第18题图
第23题图
第22题图
第7题图
第4题图
第26题图1
第10题图
第25题图
第19题图
第9题图
第15题图
第2题图
第24题图
第23题图
第26题图1
第13题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2020?2021学年度下学期七年级数学(下册)
第四章三角形检测题1
(有答案)
(时间:120分钟
满分:120分)
一、选择题
(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1、下列各组数中,不可能成为一个三角形三边长的是( )
A.3,4,5
B.1,1,1
C.5,7,12
D.5,12,15
2、如图,AC⊥BC,CD⊥AB,DE⊥AC,垂足分别为C,D,E,则下列说法不正确的是( )
A.CD是△ABC的高
B.DE是△ACD的高
C.CE是△CDE的高
D.BD是△CDE的高
3、下列说法不正确的是( )
A.全等三角形的大小、形状相同
B.全等三角形的面积相等
C.全等三角形的周长相等
D.周长相等的三角形是全等三角形
4、如图在△ABC中,已知点D、E、F分别为边BC,AB,AC的中点,且△ABC的面积是12,则阴影部分的面积是(
)
A.2
B.4
C.6
D.8
5、已知线段a,b和m,求作△ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序依次为( )
①延长CD到B,使BD=CD;②连接AB;③作△ADC,使DC=a,AC=b,AD=m.
A.③①②
B.①②③
C.②③①
D.③②①
6、如图,点A,D在线段BC的同一侧,AC与BD相交于点E,连接AB,CD,已知∠1=∠2,现添加以下哪个条件仍不能判定△ABC≌△DCB的是
(????
)
A.∠A=∠D?
???
???
B.AC=DB
C.∠ABC=∠DCB?
???????
D.AB=DC
7、如图,如果AD∥BC,AD=BC,AC与BD相交于O点,则图中的全等三角形一共有( )
A.2对
B.3对
C.4对
D.5对
8、如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=38°,∠C=50°,
则∠EAD
=(
)
A.20°
B.15°
C.12°
D.6°
9、如图,三角形纸片ABC中,将∠C沿DE折叠,使点A落在△ABC外部点处,若∠1=20°,则∠1,∠2,∠A的等量关系为(
)
A.∠1+∠2=∠A
B.∠1?∠2=2∠A
C.∠1+∠2=2∠A
D.∠2?∠1=∠A
10、如图,在△ABC中,AD为BC边上的中线,若AB=4,AC=2,则AD的取值范围是(
)
A.1
B.2
??
D.2
(每题3分,共30分)
11、在△ABC中,∠A=∠B=∠C,则此三角形是
三角形(填“直角”或“锐角”或“钝角”).
12、如图所示,要测量池塘两岸相对的两点A,B之间的距离,可先在平地上取一个可以直接到达点A和B的点O,连接AO并延长到点D,使DO=OA,连接BO并延长到C,使CO=BO,连接CD,出CD=akm,则AB两点间的距离为
.
13、如图在四边形ABCD中,若沿着直线EF剪去一个50°的解得到一个五边形,则∠1+∠2=
.
14、已知在△ABC中,第二条边的长是第一条边的3倍多3cm,第三条边的长是第二条边的2倍少17cm,若这个三角形的周长为59cm,则此三角形的三边分别为
cm,
cm,
cm.
15、如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是
.
16、如图,若△ABC是等腰三角形,a,b是其两边,且满足,则△ABC周长为
.
17、在直角三角形中,一个锐角∠A是另一个锐角∠B的3倍,则∠B度数是
.
18、如图,在△ABC中,∠B=∠C,点D在BC上DE⊥AB于点E,FD⊥BC交AC与点F.若∠AFD=142°,则∠EDF=
.
19、在△ABC中,∠ACB=90°,
∠B=60°,AE,CD分别是∠BAC和∠ACB的平分线,AE,CD相交于点F.则(1)∠DFE的度数为
;(2)
FE与FD之间的数量关系为
.
20、根据下列条件:①AB=5,AC=6,∠C=50°;②AB=3,BC=4,AC=6;③∠A=30°,∠B=45°,AB=10;④∠A=90°,BC=7;⑤AB=4,BC=5,AC=10.其中不能作出唯一的△ABC是
.(填正确的序号)
三、解答题(共6题
共60分)
21、(8分)
用一条长为32cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3.5倍,那么各边的长是多少?
(2)能围成有一边的长是8cm的等腰三角形吗?若能求出等腰三角形的三边的长;若不能说明
理由.
22、(10分)
如图△ABC中,∠A=28°,CD是∠ACB的平分线,△ADC中,DE是AC边上的高,
又有∠ADE=∠CDB,求(1)∠B的大小;(2)在∠A可取值范围内,探究∠A与∠B数量关系,
并说明理由.
23、(10分)如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.
(1)
BD与CE相等吗?为什么?
(2)试猜想BD,CE有何特殊位置关系,并说明理由.
24、(12分)
如图,已知点A,B边OM上,CD在边ON上,若OA=OC,AB=CD,AD和BC交于点P,试探究OP平分∠MON.
25、(8分)
已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)若∠A=100°,如图,求∠DHE的度数;
(2)若△ABC中∠A=50°,直接写出∠DHE的度数.
26、(12分)
如图,在△ABC中,∠ACB=90°,AC=BC,过C点任作一直线MN,过A作AD⊥MN于点D,过B作BE⊥MN于点E,
(1)如图1,当直线MN在△ABC的外部时,
DE,AD,BE有怎样的等量关系?为什么?
(2)如图2,当直线MN在△ABC的内部时,(1)中的结论是否仍然成立?若成立,说明理由;
若不成立,请指出DE与AD、BE之间的数量关系并说明理由.
参考答案
一、选择题(共10小题
每3分
共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
D
B
A
D
C
D
B
A
二、填空题(共10小题
每题3分
共30分)
11、直角三角形
12、akm
13、230°
14、7,23,29
15、108
16、20
17、
22.5°
18、52°
19、120°,FE=FD
20、①②④
三、解答题(共6题
共60分)
21、(8分)
用一条长为32cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3.5倍,那么各边的长是多少?
(2)能围成有一边的长是8cm的等腰三角形吗?若能求出等腰三角形的三边的长;若不能说明
理由.
解:(1)设底边长为xcm,则腰长为3.5xcm,则
3.5x+3.5x+x=32
解得,x=4,
∴3.5x=14,
∴各边长为:14cm,14cm,4cm.
(2)①当8cm为底时,腰长=12cm;
②当8cm为腰时,底边=16cm,因为8+8=16,故不能构成三角形,
所以能构成底边为8cm,腰长为12cm的等腰三角形.
22、(10分)
如图△ABC中,∠A=28°,CD是∠ACB的平分线,△ADC中,DE是AC边上的高,
又有∠ADE=∠CDB,求(1)∠B的大小;(2)在∠A可取值范围内,探究∠A与∠B数量关系,
并说明理由.
解:(1)∵DE是AC边上的高,
∴∠AED=∠DEC=90°,
∵∠A=28°,
∴∠ADE=90°?28°=62°,
∵∠ADE=∠CDB,
∴∠CDE=180°?62°×2=56°,
在Rt△CDE中,∠DCE=90°?56°=34°,
∵CD是∠ACB的平分线,
∴∠ACB=2∠DCE=2×34°=68°,
在△ABC中,∠B=180°?∠ACB?∠A=180°?68°?28°=84°.
(2)∠B=3∠A,理由如下:
根据(1)可得,∠ADE=90°?∠A,
∠CDB
=∠ADE
=90°?∠A,
∴∠CDE=180°?∠CDB
?∠ADE=180°?
2×(90°?∠A)=
2∠A,
在Rt△CDE中,∠DCE=90°?
2∠A,
∵CD是∠ACB的平分线,
∴∠ACB=2∠DCE=2×(90°?
2∠A)
=180°?4∠A,
在△ABC中,∠B=180°?∠ACB?∠A=180°?(180°?4∠A)
?∠A
=3∠A.
23、(10分)如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.
(1)
BD与CE相等吗?为什么?
(2)试猜想BD,CE有何特殊位置关系,并说明理由.
解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,
∵,
∴△BAD≌△CAE(SAS),
∴BD=CE;
②∵△BAD≌△CAE,
∴∠1=∠2,
∵∠AGB=∠CGD,∠BAC
=90°,
∴∠CDG=90°,
∴BD⊥CE.
24、(12分)
如图,已知点A,B边OM上,CD在边ON上,若OA=OC,AB=CD,AD和BC交于点P,试探究OP平分∠MON.
解:∵OA=OC,AB=CD,
∴OA+AB=OC+CD
即OB=OD,
在△OAD和△OCB中,
∵,
∴△OAD≌△OCB(SAS),
∴∠3=∠4,
∵∠BAP=∠AOC+∠4,∠DCP=∠COA+∠3
∴∠BAP=∠DCP
,
在△ABP和△CDP中,
∵,
∴△ABP≌△CDP(ASA),
∴PB=PD,
在△OBP和△ODP中,
∵,
∴△OBP≌△ODP(SSS),
∴∠1=∠2.
∴OP平分∠MON.
25、(8分)
已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)若∠A=100°,如图,求∠DHE的度数;
(2)若△ABC中∠A=50°,直接写出∠DHE的度数.
解:(1)∵BD、CE是△ABC的两条高,
∴∠HDA=∠HEA=90°,
∴∠DHE=180°?∠A=80°;
(2)当∠A=50°时,
①△ABC是锐角三角形时,∠DHE=180°?50°=130°;
②△ABC是钝角三角形时,∠DHE=∠A=50°;
故答案为:50°或130°.
26、(12分)
如图,在△ABC中,∠ACB=90°,AC=BC,过C点任作一直线MN,过A作AD⊥MN于点D,过B作BE⊥MN于点E,
(1)如图1,当直线MN在△ABC的外部时,
DE,AD,BE有怎样的等量关系?为什么?
(2)如图2,当直线MN在△ABC的内部时,(1)中的结论是否仍然成立?若成立,说明理由;若不成立,请指出DE与AD、BE之间的数量关系并说明理由.
(1)解:DE=AD+BE.理由如下:
∵AD⊥MN于D,
BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠1+∠3=90°,
∵∠ACB=90°,
∴∠2+∠3=90°,
∴∠1=∠2,
在△ACD和△CBE中,
∵,
∴△ACD≌△CBE(AAS),
∴AD=CE,DC=EB,
∴DE=DC+CE=AD+BE;
(2)(1)中的结论不成立,DE与AD、BE之间的数量关系为DE=BE?AD.理由如下:
∵AD⊥MN于D,
BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠5+∠6=90°,
∵∠ACB=90°,
∴∠4+∠6=90°,
∴∠4=∠5,
在△ACD和△CBE中,
∵,
∴△ACD≌△CBE(AAS),
∴AD=CE,DC=EB,
∴DE=DC?CE=BE?AD.
第8题图
第23题图
第24题图
第6题图
第26题图2
第25题图
第12题图
第26题图2
第22题图
第18题图
第23题图
第22题图
第7题图
第4题图
第26题图1
第10题图
第25题图
第19题图
第9题图
第15题图
第2题图
第24题图
第23题图
第26题图1
第13题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
