北师大版七年级下册数学课件 第三章 变量之间的关系 复习与回顾(共27张)
文档属性
| 名称 | 北师大版七年级下册数学课件 第三章 变量之间的关系 复习与回顾(共27张) |  | |
| 格式 | pptx | ||
| 文件大小 | 319.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 19:23:07 | ||
图片预览





文档简介
第三章 复习与回顾
1.知识目标:回顾总结表示变量之间的方法,学会用变量之间关系的各种形式分析变量之间的关系,并作出预测。
2.能力目标:从常量的世界走入变量的世界,开始接触一种新的思维方式——用运动变化的观点去认识数学对象,发展符号感和抽象思维。发展有条理的思考和进行表达的能力。
3.情感目标:能从运动变化的角度解释生活中的数学现象,体验成就感,获得学习的快乐,发展对数学更高层次的认识。
教学目标
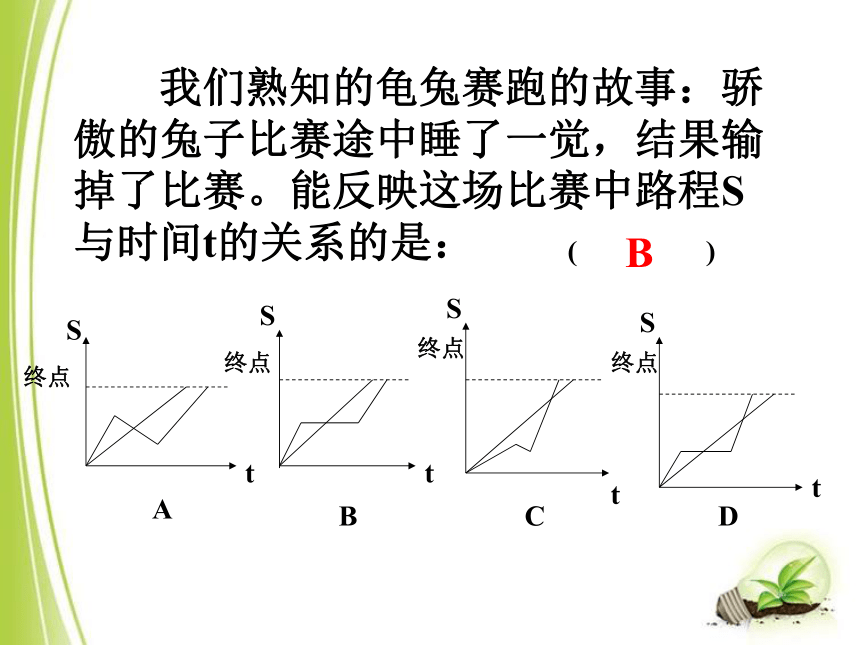
我们熟知的龟兔赛跑的故事:骄傲的兔子比赛途中睡了一觉,结果输掉了比赛。能反映这场比赛中路程S与时间t的关系的是:
t
S
终点
A
终点
t
S
B
t
终点
S
C
S
终点
t
D
( )
B
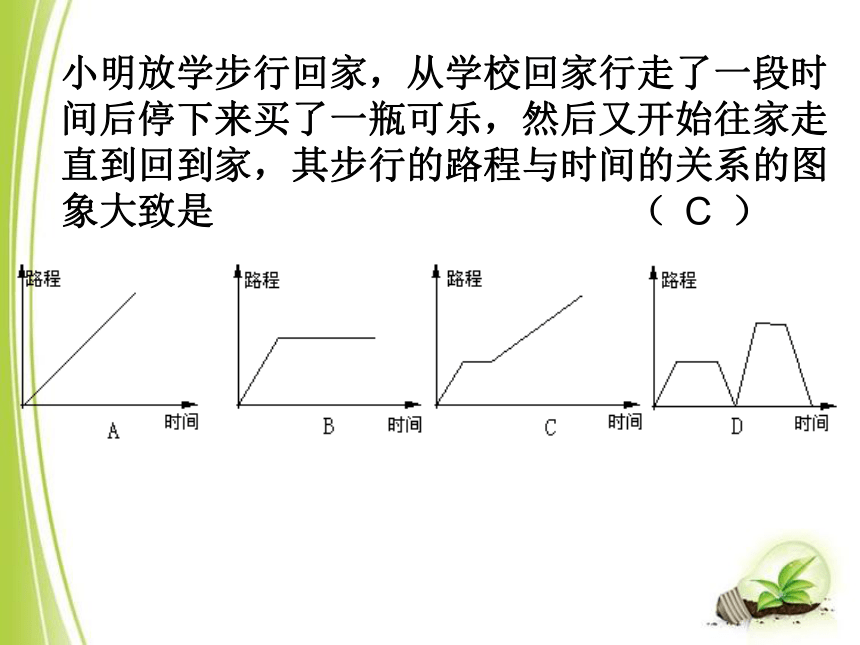
小明放学步行回家,从学校回家行走了一段时间后停下来买了一瓶可乐,然后又开始往家走直到回到家,其步行的路程与时间的关系的图象大致是 ( )
C
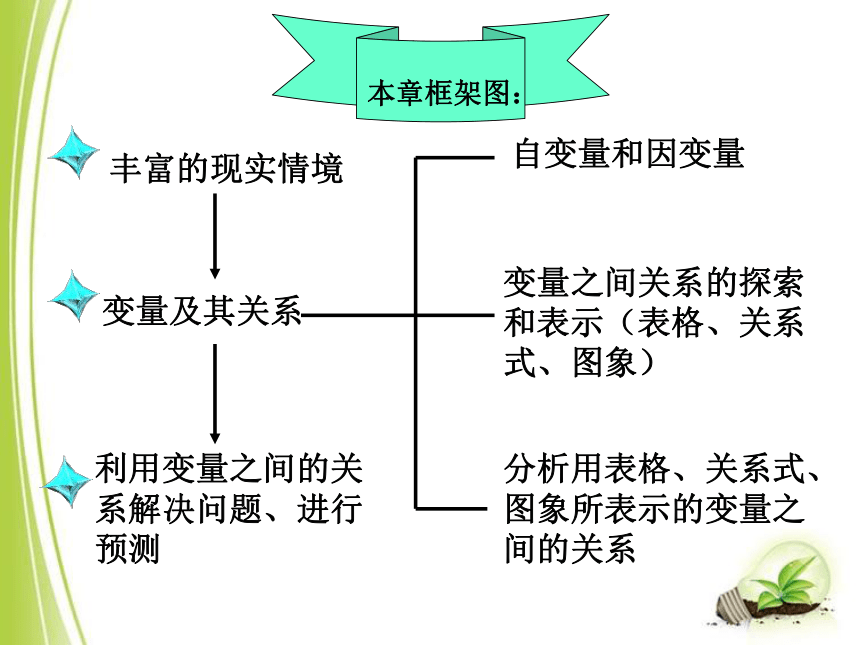
丰富的现实情境
变量及其关系
利用变量之间的关系解决问题、进行预测
自变量和因变量
变量之间关系的探索和表示(表格、关系式、图象)
分析用表格、关系式、图象所表示的变量之间的关系
本章框架图:
1、沪宁高速公路是江苏省第一条高速公路。全长267千米该路东起上海,西止于南京,连接上海、苏州、无锡、常州、镇江、南京六个大中城市。近几年,随着长江三角洲经济的飞速发展,车流量与日俱增,沪宁高速公路已不堪重负,常出现路堵现象,目前政府正在整修路面,将它扩建为双向10车道。
今年 “五一” 黄金周的一天,小强参加了“上海一日游”活动。他们的行程大概是早上由南京出发,通过沪宁高速公路直达上海,游玩结束之后原路返回南京。
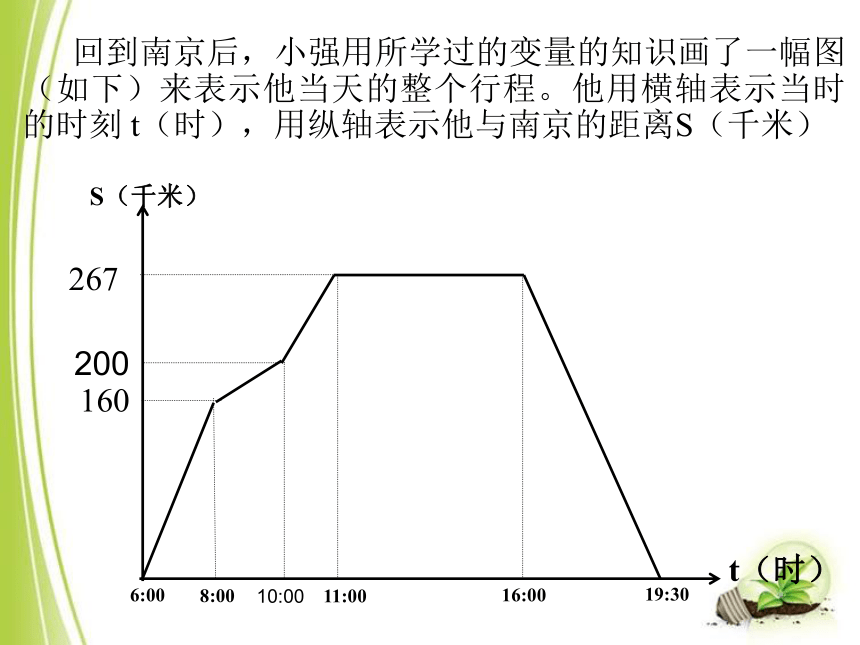
回到南京后,小强用所学过的变量的知识画了一幅图(如下)来表示他当天的整个行程。他用横轴表示当时的时刻 t(时),用纵轴表示他与南京的距离S(千米)
6:00
8:00
11:00
16:00
19:30
160
267
S(千米)
t(时)
200
10:00
看图你能回答这些问题吗?
(1)小强到达上海是什么时候?他们用了多少时间?
(2)去上海的途中,可能由于前方路堵,汽车减速慢行。你知道汽车何时开始减速吗?
(3)小强什么时候回到南京?用了多长时间?返回时的平均车速时多少?
上午11︰00左右,用了5个小时
大约上午8︰00
19︰30回到南京,用了3.5小时。
返程时平均车速为76.3千米/时。
2: 某蓄水池开始蓄水,每时进水20米3,设蓄水量为V(米3),蓄水时间为t(时)
(1)V与t之间的关系式是什么?
V=20t
2: 某蓄水池开始蓄水,每时进水20米3,设蓄水量为V(米3),蓄水时间为t(时)
(1)V与t之间的关系式是什么?
(2)用表格表示当t从2变化到8时(每次增加1),相应的V值?
V=20t
时间t(时)
2
3
4
5
6
7
8
水量V(米3)
40
60
80
100
120
140
160
2: 某蓄水池开始蓄水,每时进水20米3,设蓄水量为V(米3),蓄水时间为t(时)
(1)V与t之间的关系式是什么?
(2)用表格表示当t从2变化到8时(每次增加1),相应的V值?
(3)若蓄水池最大蓄水量为1000米3,则需要多长时间能蓄满水?
时间t(时)
2
3
4
5
6
7
8
水量V(米3)
40
60
80
100
120
140
160
V=20t
把V=1000米3代入关系式,得1000=20t,解 得 t=50(时)。
当t逐渐增加时,V也在逐渐增加
(4)V怎样随t的变化而变化?
3:甲、乙两人(甲骑自行车,乙骑摩托车)从A城出发到B城旅行。如图表示甲、乙两人离开A城的路程与时间之间关系的图象。根据图象,你能得到关于甲、乙两人旅行的那些信息?
答题要求:
(1)请至少提供四条信息。如,由图象可知:甲比乙早出发4小时(或乙比甲迟出发4小时);甲从A城到B城的平均速度是12.5千米/时
(2)请不要再提供(1)中已列举的信息。
路程(千米)
摩托车
自行车
时间(小时)
参考答案:
(1)本次旅行甲用了8小时
(2)甲比乙晚到2小时
(3)甲出发3小时后走了全程的一半
(4)乙一共用了2个小时
4.一壶正在烧的水,水的温度与时间的关系的图象大致是 ( )
B
5.小颖向平静的湖面扔了一粒石子,水面上出现了一圈一圈的水波,如图:
(1)观察这些水波随着时间的变化如何变化?
(2)在这个变化过程中,找出因变量和自变量;
(3)设圆的面积为s ,半径为r ,当半径从1厘米变化到5厘米时,面积如何变化?
汽车行驶时间 t(小时)
0
1
2
4
6
油箱的油量 Q (升)
60
6、某种油箱容量为60升的汽车,加满汽油后汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的 关系式 如下:Q=60-6t
(1) 请完成下表 :
(2) 汽车行驶5小时后,油箱中油量是____升
48
54
30
36
24
(3)若汽车行驶中油箱油量为12升,
则汽车行驶了___小时
(4)贮满60升汽油的汽车,
最多行驶_____小时
(5)下面哪个图象能够反映此变化过程中Q与 t 的关系: ( )
Q
t
(A)
Q
t
(B)
Q
t
(C)
A
某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的关系式如下:Q=60-6t
8
10
汽车行驶的时间 t(小时)
0
1
2
4
6
油箱的油量 Q (升)
60
54
48
36
24
7、某机动车出发前油箱内有42L油,途中在加油站加油若干L,油箱中剩余油量Q(L)与t(h)之间的关系如图所示,根据图象回答问题:
(1)机动车行驶几小时后加油?
(2)中途加油____L;
(3)如果加油站
距目的地还有240
km,车速为40km/h
要到达目的地,
油箱中的油是否
够用?说明原因.
5h
24
油箱中的油够用;理由:因为机动车每小时耗油(42-12)÷5=6L,所以240÷40×6=36L,正好够用
8.某电影院共有30排座位,第1排有20个座位,后面每排比前一排多1个座位.
(1)第9排有多少个座位?第22排呢?
(2)把每排的座位数y用这排的排数x表示出来;
(3)某一排的座位可能是50吗?为什么?
(1) 28 , 41;
(2) y=20+(x-1)=x+19;
(3) 不可能,当y=50时,x+19=50,解得x=31,∵31>30,∴不可能有50个座位。
9.某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路,如果汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(km)
与时间x(h)之间的关系
如图所示,那么汽车在
乡村公路上的行驶速度
为_____km/h.
记者从出发到目的地
共用____h。
60
5
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(1)上表反映了弹簧长度L与物体质量x之间的关系;自变量:物体质量x;因变量:弹簧长度L;
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体质量为3kg时,弹簧的长度为多少?
(2) 13.5cm
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体质量为3kg时,弹簧的长度为多少?
(3)当x增加时,L怎样变化?
(3) 当x增加时,L也随之增加;
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体质量为3kg时,弹簧的长度为多少?
(3)当x增加时,L怎样变化?
(4)写出L与x的关系式;
(4) L=12+0.5x;
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体质量为3kg时,弹簧的长度为多少?
(3)当x增加时,L怎样变化?
(4)写出L与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度。
(5) 当x=2.5时,L=12+0.5×2.5=13.25cm
小结:
通过对变量的相关知识的复习和整理,今后我们要用变化的观念考虑问题,多多用变量的思想去分析问题。先找出问题中存在的变量,确定自变量与因变量,然后结合实际通过恰当的变量表示法表示变量之间的关系,并进行分析。
1.知识目标:回顾总结表示变量之间的方法,学会用变量之间关系的各种形式分析变量之间的关系,并作出预测。
2.能力目标:从常量的世界走入变量的世界,开始接触一种新的思维方式——用运动变化的观点去认识数学对象,发展符号感和抽象思维。发展有条理的思考和进行表达的能力。
3.情感目标:能从运动变化的角度解释生活中的数学现象,体验成就感,获得学习的快乐,发展对数学更高层次的认识。
教学目标
我们熟知的龟兔赛跑的故事:骄傲的兔子比赛途中睡了一觉,结果输掉了比赛。能反映这场比赛中路程S与时间t的关系的是:
t
S
终点
A
终点
t
S
B
t
终点
S
C
S
终点
t
D
( )
B
小明放学步行回家,从学校回家行走了一段时间后停下来买了一瓶可乐,然后又开始往家走直到回到家,其步行的路程与时间的关系的图象大致是 ( )
C
丰富的现实情境
变量及其关系
利用变量之间的关系解决问题、进行预测
自变量和因变量
变量之间关系的探索和表示(表格、关系式、图象)
分析用表格、关系式、图象所表示的变量之间的关系
本章框架图:
1、沪宁高速公路是江苏省第一条高速公路。全长267千米该路东起上海,西止于南京,连接上海、苏州、无锡、常州、镇江、南京六个大中城市。近几年,随着长江三角洲经济的飞速发展,车流量与日俱增,沪宁高速公路已不堪重负,常出现路堵现象,目前政府正在整修路面,将它扩建为双向10车道。
今年 “五一” 黄金周的一天,小强参加了“上海一日游”活动。他们的行程大概是早上由南京出发,通过沪宁高速公路直达上海,游玩结束之后原路返回南京。
回到南京后,小强用所学过的变量的知识画了一幅图(如下)来表示他当天的整个行程。他用横轴表示当时的时刻 t(时),用纵轴表示他与南京的距离S(千米)
6:00
8:00
11:00
16:00
19:30
160
267
S(千米)
t(时)
200
10:00
看图你能回答这些问题吗?
(1)小强到达上海是什么时候?他们用了多少时间?
(2)去上海的途中,可能由于前方路堵,汽车减速慢行。你知道汽车何时开始减速吗?
(3)小强什么时候回到南京?用了多长时间?返回时的平均车速时多少?
上午11︰00左右,用了5个小时
大约上午8︰00
19︰30回到南京,用了3.5小时。
返程时平均车速为76.3千米/时。
2: 某蓄水池开始蓄水,每时进水20米3,设蓄水量为V(米3),蓄水时间为t(时)
(1)V与t之间的关系式是什么?
V=20t
2: 某蓄水池开始蓄水,每时进水20米3,设蓄水量为V(米3),蓄水时间为t(时)
(1)V与t之间的关系式是什么?
(2)用表格表示当t从2变化到8时(每次增加1),相应的V值?
V=20t
时间t(时)
2
3
4
5
6
7
8
水量V(米3)
40
60
80
100
120
140
160
2: 某蓄水池开始蓄水,每时进水20米3,设蓄水量为V(米3),蓄水时间为t(时)
(1)V与t之间的关系式是什么?
(2)用表格表示当t从2变化到8时(每次增加1),相应的V值?
(3)若蓄水池最大蓄水量为1000米3,则需要多长时间能蓄满水?
时间t(时)
2
3
4
5
6
7
8
水量V(米3)
40
60
80
100
120
140
160
V=20t
把V=1000米3代入关系式,得1000=20t,解 得 t=50(时)。
当t逐渐增加时,V也在逐渐增加
(4)V怎样随t的变化而变化?
3:甲、乙两人(甲骑自行车,乙骑摩托车)从A城出发到B城旅行。如图表示甲、乙两人离开A城的路程与时间之间关系的图象。根据图象,你能得到关于甲、乙两人旅行的那些信息?
答题要求:
(1)请至少提供四条信息。如,由图象可知:甲比乙早出发4小时(或乙比甲迟出发4小时);甲从A城到B城的平均速度是12.5千米/时
(2)请不要再提供(1)中已列举的信息。
路程(千米)
摩托车
自行车
时间(小时)
参考答案:
(1)本次旅行甲用了8小时
(2)甲比乙晚到2小时
(3)甲出发3小时后走了全程的一半
(4)乙一共用了2个小时
4.一壶正在烧的水,水的温度与时间的关系的图象大致是 ( )
B
5.小颖向平静的湖面扔了一粒石子,水面上出现了一圈一圈的水波,如图:
(1)观察这些水波随着时间的变化如何变化?
(2)在这个变化过程中,找出因变量和自变量;
(3)设圆的面积为s ,半径为r ,当半径从1厘米变化到5厘米时,面积如何变化?
汽车行驶时间 t(小时)
0
1
2
4
6
油箱的油量 Q (升)
60
6、某种油箱容量为60升的汽车,加满汽油后汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的 关系式 如下:Q=60-6t
(1) 请完成下表 :
(2) 汽车行驶5小时后,油箱中油量是____升
48
54
30
36
24
(3)若汽车行驶中油箱油量为12升,
则汽车行驶了___小时
(4)贮满60升汽油的汽车,
最多行驶_____小时
(5)下面哪个图象能够反映此变化过程中Q与 t 的关系: ( )
Q
t
(A)
Q
t
(B)
Q
t
(C)
A
某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(时)变化的关系式如下:Q=60-6t
8
10
汽车行驶的时间 t(小时)
0
1
2
4
6
油箱的油量 Q (升)
60
54
48
36
24
7、某机动车出发前油箱内有42L油,途中在加油站加油若干L,油箱中剩余油量Q(L)与t(h)之间的关系如图所示,根据图象回答问题:
(1)机动车行驶几小时后加油?
(2)中途加油____L;
(3)如果加油站
距目的地还有240
km,车速为40km/h
要到达目的地,
油箱中的油是否
够用?说明原因.
5h
24
油箱中的油够用;理由:因为机动车每小时耗油(42-12)÷5=6L,所以240÷40×6=36L,正好够用
8.某电影院共有30排座位,第1排有20个座位,后面每排比前一排多1个座位.
(1)第9排有多少个座位?第22排呢?
(2)把每排的座位数y用这排的排数x表示出来;
(3)某一排的座位可能是50吗?为什么?
(1) 28 , 41;
(2) y=20+(x-1)=x+19;
(3) 不可能,当y=50时,x+19=50,解得x=31,∵31>30,∴不可能有50个座位。
9.某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路,如果汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(km)
与时间x(h)之间的关系
如图所示,那么汽车在
乡村公路上的行驶速度
为_____km/h.
记者从出发到目的地
共用____h。
60
5
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(1)上表反映了弹簧长度L与物体质量x之间的关系;自变量:物体质量x;因变量:弹簧长度L;
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体质量为3kg时,弹簧的长度为多少?
(2) 13.5cm
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体质量为3kg时,弹簧的长度为多少?
(3)当x增加时,L怎样变化?
(3) 当x增加时,L也随之增加;
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体质量为3kg时,弹簧的长度为多少?
(3)当x增加时,L怎样变化?
(4)写出L与x的关系式;
(4) L=12+0.5x;
10.已知一弹簧的长度L(cm)与所挂重物的质量x(kg)之间的关系如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
1
2
3
4
5
L
12
12.5
13
13.5
14
14.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体质量为3kg时,弹簧的长度为多少?
(3)当x增加时,L怎样变化?
(4)写出L与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度。
(5) 当x=2.5时,L=12+0.5×2.5=13.25cm
小结:
通过对变量的相关知识的复习和整理,今后我们要用变化的观念考虑问题,多多用变量的思想去分析问题。先找出问题中存在的变量,确定自变量与因变量,然后结合实际通过恰当的变量表示法表示变量之间的关系,并进行分析。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
