六年级数学下册试题 一课一练1.1《面的旋转》习题1-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练1.1《面的旋转》习题1-北师大版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 16:03:15 | ||
图片预览



文档简介
1.1《面的旋转》习题1
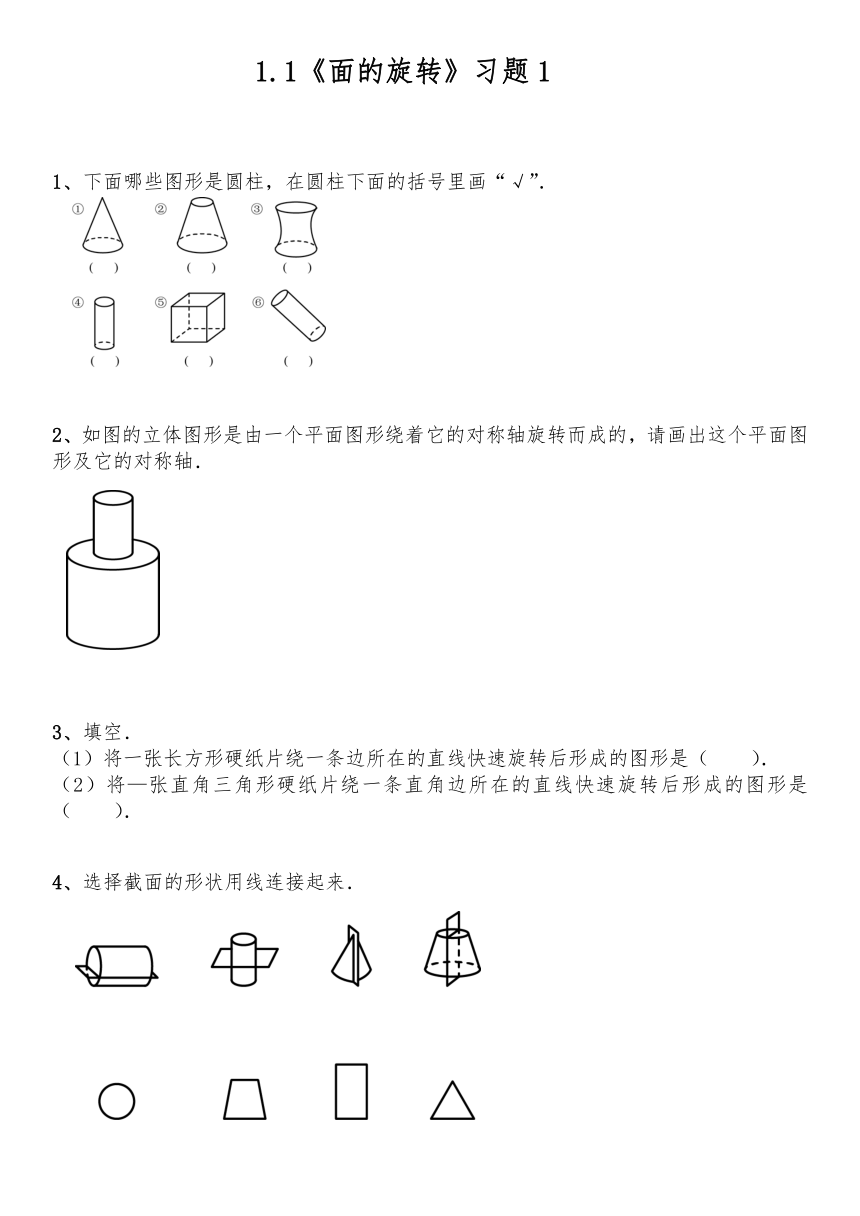
1、下面哪些图形是圆柱,在圆柱下面的括号里画“√”.
2、如图的立体图形是由一个平面图形绕着它的对称轴旋转而成的,请画出这个平面图形及它的对称轴.
3、填空.
(1)将一张长方形硬纸片绕一条边所在的直线快速旋转后形成的图形是(
).
(2)将—张直角三角形硬纸片绕一条直角边所在的直线快速旋转后形成的图形是(
).
4、选择截面的形状用线连接起来.
5、请你在圆柱的下面画“√”,不是圆柱的画“×”.
6、如图,切完后的截面分别是什么形状?连一连.
7、上面一排图形旋转后会得到下面的哪个图形?想一想,连一连.
8、填空.
(1)圆柱是由(
)个面围成的,圆柱的上、下两个面叫做(
),圆柱周围的面(上、下底面除外)叫做(
),圆柱的两个底面之间的距离叫做(
).
(2)如下图所示,将长方形ABCD以边AB所在的直线为轴旋转一周,形成一个(
),它的底面半径是(
)cm,高是(
)cm,每个底面的面积是(
)cm2.
9、填一填.
(1)圆柱的侧面展开后是一个(
)形.当圆柱的侧面展开后是一个正方形时,这个圆柱的(
)与高相等.
(2)一个长方体,最多有(
)个面是长方形(不含正方形),最少有(
)个面是长方形.
(3)从一个方向观察物体,一次最多只能看到(
)个面.
10、对照图①,在图②中填上合适的名称.
11、一个圆柱的底面半径是4.5cm它的侧面展开图是正方形,这个圆柱的高是多少厘米?
12、一张正方形纸卷成一个圆柱,求这个圆柱的高与底面直径的比.
13、填一填.
(1)圆柱的两个底面之间的距离叫做圆柱的(
).
(2)把图1“底面”“底面的周长”“高”分别填入图2的圆柱侧面展开图中的合适位置.
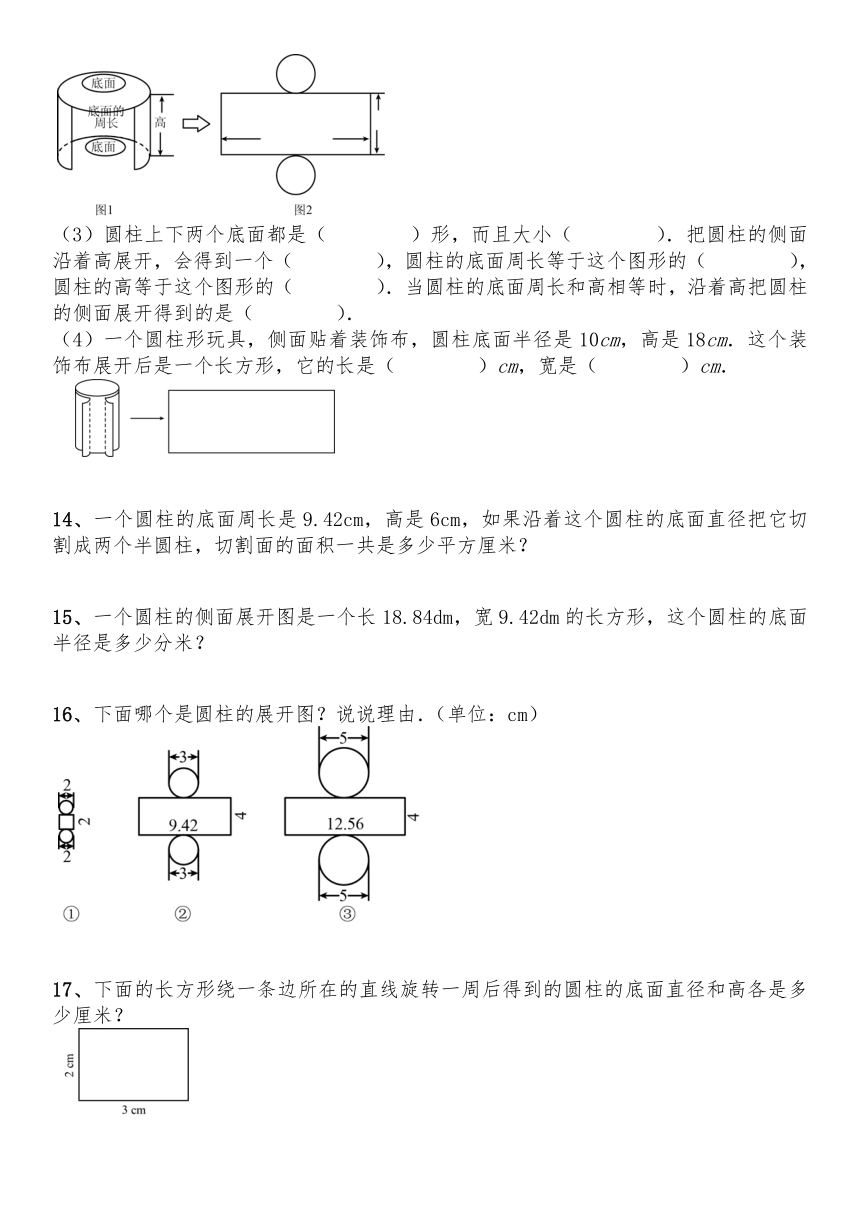
(3)圆柱上下两个底面都是(
)形,而且大小(
).把圆柱的侧面沿着高展开,会得到一个(
),圆柱的底面周长等于这个图形的(
),圆柱的高等于这个图形的(
).当圆柱的底面周长和高相等时,沿着高把圆柱的侧面展开得到的是(
).
(4)一个圆柱形玩具,侧面贴着装饰布,圆柱底面半径是10cm,高是18cm.这个装饰布展开后是一个长方形,它的长是(
)cm,宽是(
)cm.
14、一个圆柱的底面周长是9.42cm,高是6cm,如果沿着这个圆柱的底面直径把它切割成两个半圆柱,切割面的面积一共是多少平方厘米?
15、一个圆柱的侧面展开图是一个长18.84dm,宽9.42dm的长方形,这个圆柱的底面半径是多少分米?
16、下面哪个是圆柱的展开图?说说理由.(单位:cm)
17、下面的长方形绕一条边所在的直线旋转一周后得到的圆柱的底面直径和高各是多少厘米?
18、用一块长28.26cm,宽15.7cm的长方形铁皮,配上圆形铁皮的直径为(
)时,可以做成容积最大的圆柱.
A.4.5cm
B.9cm
C.5cm
D.2.5cm
19、小法官,巧判断.(下列图形中是圆锥的画“√”,不是圆锥的画“×”)
20、(创新能力题)转一转,想一想会产生哪种立体图形,用线连一连.
21、折一折,想一想,能得到什么图形,把下面所对应图形的编号写在括号里.
22、连一连.(上面一排图形旋转后是下面的哪个立体图形)
答案
1、④(√)
⑥(√)
2、
3、(1)一个圆柱;
(2)一个圆锥;
4、略;
5、略
6、略
7、略
8、(1)3
底面
侧面
高
(2)圆柱
6
3
113.04
9、(1)长方;底面周长(2)6;4(3)3
10、
11、2×3.14×4.5=28.26(cm)
12、
13、(1)高
(2)略
(3)圆相等长方形长宽正方形
(4)62.8
18
14、9.42÷3.14×6×2=36(cm2)
15、18.84÷3.14÷2=3(dm)或9.42÷3.14÷2=1.5(dm)
16、②是圆柱的展开图,因为底面周长3×3.14=9.42(cm)正好是长方形的长.
①和③都不是.
17、以一条宽边所在的直线为轴旋转:
底面直径为3×2=6(cm),高为2cm;
以一条长边所在的直线为轴旋转:
底面直径为2×2=4(cm),高为3cm;
18、B
19、×,√,√
20、
21、①②⑤④③⑥
22、略
1、下面哪些图形是圆柱,在圆柱下面的括号里画“√”.
2、如图的立体图形是由一个平面图形绕着它的对称轴旋转而成的,请画出这个平面图形及它的对称轴.
3、填空.
(1)将一张长方形硬纸片绕一条边所在的直线快速旋转后形成的图形是(
).
(2)将—张直角三角形硬纸片绕一条直角边所在的直线快速旋转后形成的图形是(
).
4、选择截面的形状用线连接起来.
5、请你在圆柱的下面画“√”,不是圆柱的画“×”.
6、如图,切完后的截面分别是什么形状?连一连.
7、上面一排图形旋转后会得到下面的哪个图形?想一想,连一连.
8、填空.
(1)圆柱是由(
)个面围成的,圆柱的上、下两个面叫做(
),圆柱周围的面(上、下底面除外)叫做(
),圆柱的两个底面之间的距离叫做(
).
(2)如下图所示,将长方形ABCD以边AB所在的直线为轴旋转一周,形成一个(
),它的底面半径是(
)cm,高是(
)cm,每个底面的面积是(
)cm2.
9、填一填.
(1)圆柱的侧面展开后是一个(
)形.当圆柱的侧面展开后是一个正方形时,这个圆柱的(
)与高相等.
(2)一个长方体,最多有(
)个面是长方形(不含正方形),最少有(
)个面是长方形.
(3)从一个方向观察物体,一次最多只能看到(
)个面.
10、对照图①,在图②中填上合适的名称.
11、一个圆柱的底面半径是4.5cm它的侧面展开图是正方形,这个圆柱的高是多少厘米?
12、一张正方形纸卷成一个圆柱,求这个圆柱的高与底面直径的比.
13、填一填.
(1)圆柱的两个底面之间的距离叫做圆柱的(
).
(2)把图1“底面”“底面的周长”“高”分别填入图2的圆柱侧面展开图中的合适位置.
(3)圆柱上下两个底面都是(
)形,而且大小(
).把圆柱的侧面沿着高展开,会得到一个(
),圆柱的底面周长等于这个图形的(
),圆柱的高等于这个图形的(
).当圆柱的底面周长和高相等时,沿着高把圆柱的侧面展开得到的是(
).
(4)一个圆柱形玩具,侧面贴着装饰布,圆柱底面半径是10cm,高是18cm.这个装饰布展开后是一个长方形,它的长是(
)cm,宽是(
)cm.
14、一个圆柱的底面周长是9.42cm,高是6cm,如果沿着这个圆柱的底面直径把它切割成两个半圆柱,切割面的面积一共是多少平方厘米?
15、一个圆柱的侧面展开图是一个长18.84dm,宽9.42dm的长方形,这个圆柱的底面半径是多少分米?
16、下面哪个是圆柱的展开图?说说理由.(单位:cm)
17、下面的长方形绕一条边所在的直线旋转一周后得到的圆柱的底面直径和高各是多少厘米?
18、用一块长28.26cm,宽15.7cm的长方形铁皮,配上圆形铁皮的直径为(
)时,可以做成容积最大的圆柱.
A.4.5cm
B.9cm
C.5cm
D.2.5cm
19、小法官,巧判断.(下列图形中是圆锥的画“√”,不是圆锥的画“×”)
20、(创新能力题)转一转,想一想会产生哪种立体图形,用线连一连.
21、折一折,想一想,能得到什么图形,把下面所对应图形的编号写在括号里.
22、连一连.(上面一排图形旋转后是下面的哪个立体图形)
答案
1、④(√)
⑥(√)
2、
3、(1)一个圆柱;
(2)一个圆锥;
4、略;
5、略
6、略
7、略
8、(1)3
底面
侧面
高
(2)圆柱
6
3
113.04
9、(1)长方;底面周长(2)6;4(3)3
10、
11、2×3.14×4.5=28.26(cm)
12、
13、(1)高
(2)略
(3)圆相等长方形长宽正方形
(4)62.8
18
14、9.42÷3.14×6×2=36(cm2)
15、18.84÷3.14÷2=3(dm)或9.42÷3.14÷2=1.5(dm)
16、②是圆柱的展开图,因为底面周长3×3.14=9.42(cm)正好是长方形的长.
①和③都不是.
17、以一条宽边所在的直线为轴旋转:
底面直径为3×2=6(cm),高为2cm;
以一条长边所在的直线为轴旋转:
底面直径为2×2=4(cm),高为3cm;
18、B
19、×,√,√
20、
21、①②⑤④③⑥
22、略
