六年级数学下册试题 一课一练2.1《比例的认识》-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练2.1《比例的认识》-北师大版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 258.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 00:00:00 | ||
图片预览


文档简介
2.1《比例的认识》
1、选择
(1)下面的数中,能与6、9、10组成比例的是(
).
A.7
B.5.4
C.1.5
D.2.4
(2)、在一个比例里,两个内项分别扩大到原来的3倍,如果仍然组成比例,那么两个外项的积(
).
A.扩大为原来的3倍
B.不变
C.扩大为原来的9倍
D.不能确定
(3)下列各式中(
)是比例.
①8︰2=4
②2×10=4×5
③0.6︰3=1︰5
(4)能与组成比例的是(
).
①
②4︰3
③3︰4
(5)75、50和30这三个数可以与(
)组成一个比例.
①20
②25
③35
(6)下面每组中的四个数,可以组成比例的是(
).
①0.3,4.5,0.5和
②0.3,4.5,和
③1.2,1.6,和
(7)、下列四组比中,不能与组成比例的是(
).
A.
B.
C.
D.
2、所铺正方形地面的面积一定时,每块方砖的边长和需要的块数成比例关系吗?为什么?
3、填空.
(1)表示(
)的式子叫做比例.
(2)18︰24的比值是(
),6︰8的比值是(
),它们的比值(
),组成的比例可以写成(
),也可以写成.
(3)写出比值是2的两个比(
)和(
),组成的比例是(
).
4、判断.(对的画“√”,错的画“×”)
(1)6︰10和可以组成比例.(
)
(2)8︰2=4是比例.(
)
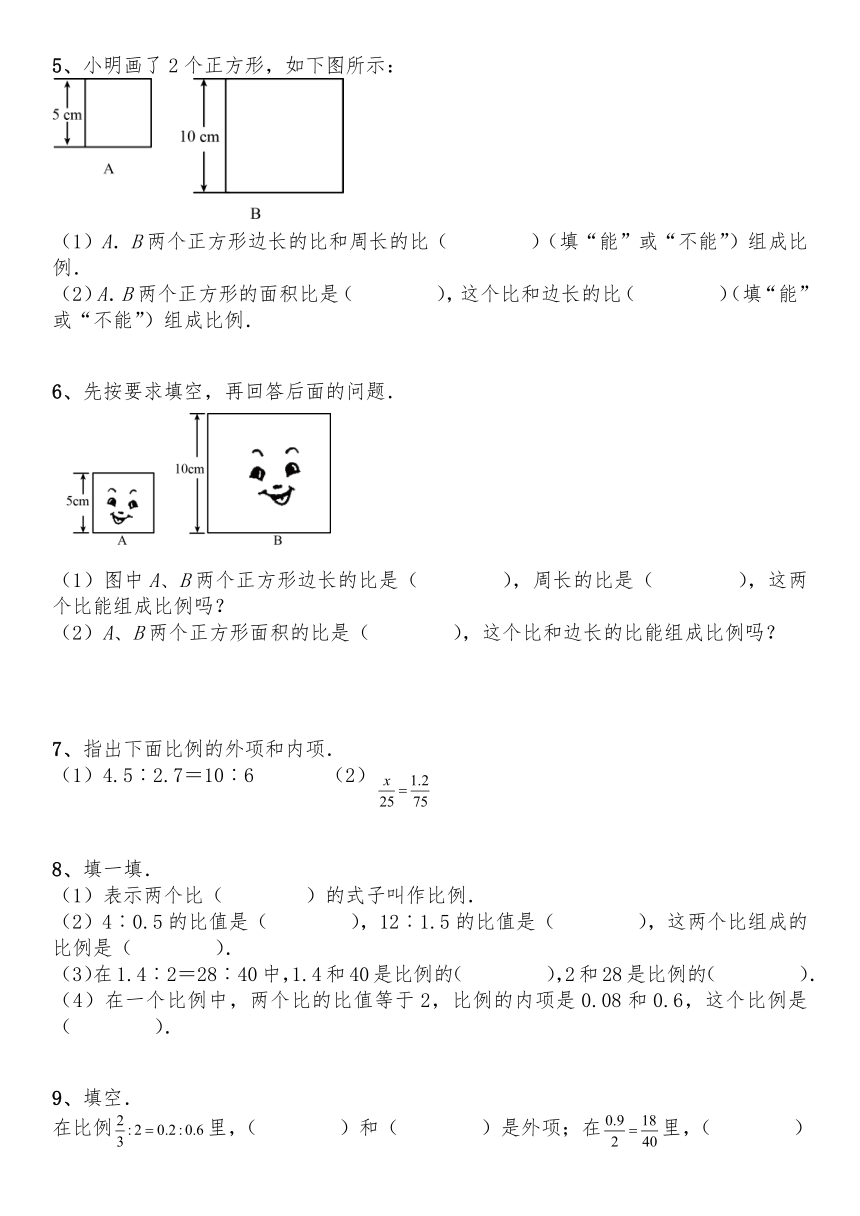
5、小明画了2个正方形,如下图所示:
(1)A.B两个正方形边长的比和周长的比(
)(填“能”或“不能”)组成比例.
(2)A.B两个正方形的面积比是(
),这个比和边长的比(
)(填“能”或“不能”)组成比例.
6、先按要求填空,再回答后面的问题.
(1)图中A、B两个正方形边长的比是(
),周长的比是(
),这两个比能组成比例吗?
(2)A、B两个正方形面积的比是(
),这个比和边长的比能组成比例吗?
7、指出下面比例的外项和内项.
(1)4.5︰2.7=10︰6
(2)
8、填一填.
(1)表示两个比(
)的式子叫作比例.
(2)4︰0.5的比值是(
),12︰1.5的比值是(
),这两个比组成的比例是(
).
(3)在1.4︰2=28︰40中,1.4和40是比例的(
),2和28是比例的(
).
(4)在一个比例中,两个比的比值等于2,比例的内项是0.08和0.6,这个比例是(
).
9、填空.
在比例里,(
)和(
)是外项;在里,(
)和(
)是内项.
10、如果4m=5n,那么m︰n=(
)
11、在一个比例里,两个内项互为倒数,其中一个外项是10以内既是奇数又是合数的数,则另一个外项是________.
12、一个长方形的周长是260cm,如果它的长减少,宽增加,就得到一个周长相等的长方形.原来长方形的面积是多少平方厘米?
13、把a×b=c×d(a,b,c,d均不为0)改写成比例式,你可以写出几个?
14、两个比的比值都是,它们组成的比例的外项分别是和,写出这个比例.
15、在12、8、16中添上一个数组成比例,这样的数你能写出几个?把可以组成的比例写出来(每个数写一个比例).
16、根据比例的基本性质,把下面的等积式改成比例式.
(1)3.6×5=2×9
(2)
17、应用比例的基本性质,判断下面各组中的两个比能否组成比例.
(1)5︰7和8︰13
(2)和
(3)和
(4)2.4︰5和4.8︰10
18、应用比例内项的积与外项的积的关系,判断下面哪几组的两个比可以组成比例,并写出组成的比例.
(1)2.8︰4和7︰10
_____________________________________________________
(2)2.7︰8和
_________________________________________
(3)3︰0.5和21︰3.5
________________________________________
19、奇思5分跑了1500m,妙想8分跑了2400m.
(1)奇思跑步的路程和时间的比是(
)︰(
).
(2)妙想跑步的路程和时间的比是(
)︰(
).
(3)这两个比能组成比例吗?为什么?如果能组成比例,请在下面写出比例.
20、把能组成比例的两个比连起来.
0.8︰3.2
5︰8
2.5︰4
10︰4
4.5︰18
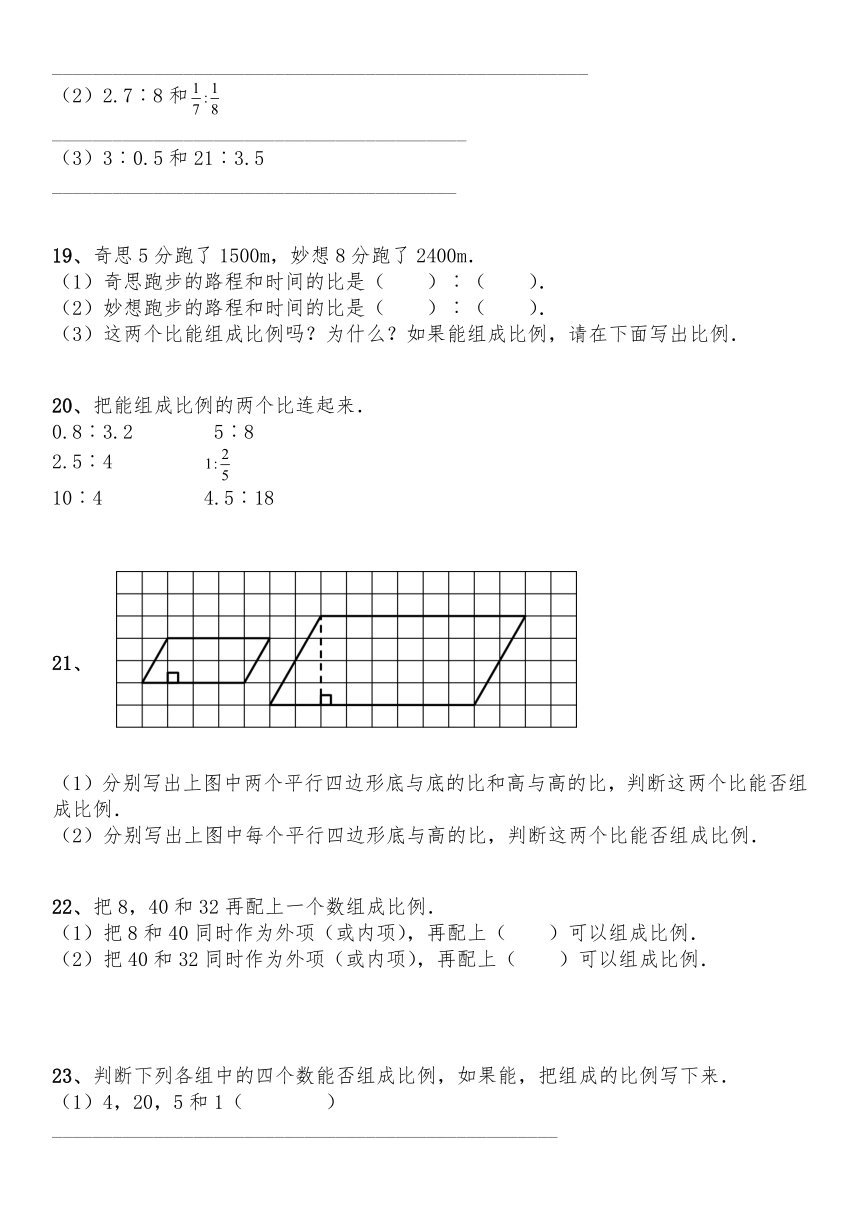
21、
(1)分别写出上图中两个平行四边形底与底的比和高与高的比,判断这两个比能否组成比例.
(2)分别写出上图中每个平行四边形底与高的比,判断这两个比能否组成比例.
22、把8,40和32再配上一个数组成比例.
(1)把8和40同时作为外项(或内项),再配上(
)可以组成比例.
(2)把40和32同时作为外项(或内项),再配上(
)可以组成比例.
23、判断下列各组中的四个数能否组成比例,如果能,把组成的比例写下来.
(1)4,20,5和1(
)
__________________________________________________
(2)3,8,40和15(
)
___________________________________________
(3)2,0.6,5和2.5(
)
_________________________________________
(4),,30和24(
)
24、判断下面各组中的两个比能否组成比例,如果能,请写出来.
(1)4︰5和
(2)4.5︰1.5和
25、填空.
在比例中,(
)和(
)是外项;
在中,(
)和(
)是内项.
26、一根绳子,先用去40m,又用去余下长度的,这时余下的绳子正好是原来总长度的.求绳子原来长多少米.
27、学校体育室有排球、足球共48只,当排球借出,足球借出时,余下的排球与足球一样多.原来排球、足球各有多少只?
28、在括号里填上合适的数,便比例成立.
(1)8︰6=4.6︰(
)
(2)3.5︰(
)=1.4︰2
(3)
(4)
(5)
(6)
29、根据比例的基本性质,判断下面各表中相对应的两个量的比能否组成比例,如果能,把组成的比例写出来.
30、下面哪几组的两个比可以组成比例?把组成的比例写出来.
(1)6︰10和9︰15
(2)0.6︰0.2和
(3)1.5︰2和
(4)和
答案
1、(1)B(2)C(3)③(4)②(5)①(6)①(7)B
2、不成比例关系.因为边长×边长×块数=所铺正方形地面的面积.
3、(1)两个比相等
(2)0.75
0.75
相等
18:24=6:8
(3)略
4、(1)×
(2)×
5、(1)能
(2)1:4
不能
6、(1)5:10
20:40
5:10=20:40(2)25:100
不能
7、(1)4.5和6是外项,2.7和10是内项
(2)x和75是外项,1.2和25是内项
8、(1)相等(2)8,8,(3)外项,内项(4)0.16:0.08=0.6:0.3
9、
0.6
2
18
10、4︰5.
11、
12、长×=宽×
长:宽=:=8:5
面积:(×)×(×)=4000(cm)
13、8个,分别是a:c=d:b
b:c=d:a
c:a=b:d
d:a=b:c
a:d=c:b
b:d=c:a
c:b=a:d
d:b=a:c
14、=
15、3个,分别是6,24,.12:16=6:8
12:8=24:16
8:=12:16(所写比例不唯一)
16、(1)(答案不唯一)
(2)4:5=(答案不唯一)
17、(1)不能(2)能(3)能(4)能
18、(1)能组成比例,2.8︰4=7︰10,7︰10=2.8︰4
(2)不能组成比例
(3)能组成比例,3︰0.5=21︰3.5,21︰3.5=3︰0.5
19、(1)1500,5
(2)2400,8
(3)能组成比例,因为它们的比值相等.1500︰5=2400︰8,2400︰8=1500︰5
20、把能组成比例的两个比连起来.
0.8︰3.2
5︰8
2.5︰4
10︰4
4.5︰18
21、(1)底的比:4:8,高的比:2:4;两个平行四边形底的比值,高的比值都是,这两个比能组成比例,即4:8=2:4;
(2)左图中底:高=4:2,右图中底:高=8:4,每个平行四边形底与高的比值都是2,这两个比能组成比例,即4:2=8:4
22、(1)10
(2)160
23、(1)
能
20:4=5:1(所写比例不唯一)
(2)
能
40:8=15:3(所写比例不唯一)
(3)不能
(4)能
=24:30(所写比例不唯一)
24、(1)能
4:5=
(2)能
4.5:1.5=
25、,0.6,2,18
26、因为第一次余下长度×(1-)=原来总长度×,
所以第一次余下长度:原来总长度=:(1-)=5:9
绳子原来长:40÷(1-)=90(m)
27、因为排球×(1-)=足球×(1-),
所以排球:足球=:=3:5
排球:48×=18(只)
足球:48-18=30(只)
28、(1)3.45(2)5(3)(4)2.4
(5)(6)
29、能
210:3=560:8
能
11:27.5=16:40
不能
30、(1)能,6:10=9:15(2)能,(3)不能(4)能
1、选择
(1)下面的数中,能与6、9、10组成比例的是(
).
A.7
B.5.4
C.1.5
D.2.4
(2)、在一个比例里,两个内项分别扩大到原来的3倍,如果仍然组成比例,那么两个外项的积(
).
A.扩大为原来的3倍
B.不变
C.扩大为原来的9倍
D.不能确定
(3)下列各式中(
)是比例.
①8︰2=4
②2×10=4×5
③0.6︰3=1︰5
(4)能与组成比例的是(
).
①
②4︰3
③3︰4
(5)75、50和30这三个数可以与(
)组成一个比例.
①20
②25
③35
(6)下面每组中的四个数,可以组成比例的是(
).
①0.3,4.5,0.5和
②0.3,4.5,和
③1.2,1.6,和
(7)、下列四组比中,不能与组成比例的是(
).
A.
B.
C.
D.
2、所铺正方形地面的面积一定时,每块方砖的边长和需要的块数成比例关系吗?为什么?
3、填空.
(1)表示(
)的式子叫做比例.
(2)18︰24的比值是(
),6︰8的比值是(
),它们的比值(
),组成的比例可以写成(
),也可以写成.
(3)写出比值是2的两个比(
)和(
),组成的比例是(
).
4、判断.(对的画“√”,错的画“×”)
(1)6︰10和可以组成比例.(
)
(2)8︰2=4是比例.(
)
5、小明画了2个正方形,如下图所示:
(1)A.B两个正方形边长的比和周长的比(
)(填“能”或“不能”)组成比例.
(2)A.B两个正方形的面积比是(
),这个比和边长的比(
)(填“能”或“不能”)组成比例.
6、先按要求填空,再回答后面的问题.
(1)图中A、B两个正方形边长的比是(
),周长的比是(
),这两个比能组成比例吗?
(2)A、B两个正方形面积的比是(
),这个比和边长的比能组成比例吗?
7、指出下面比例的外项和内项.
(1)4.5︰2.7=10︰6
(2)
8、填一填.
(1)表示两个比(
)的式子叫作比例.
(2)4︰0.5的比值是(
),12︰1.5的比值是(
),这两个比组成的比例是(
).
(3)在1.4︰2=28︰40中,1.4和40是比例的(
),2和28是比例的(
).
(4)在一个比例中,两个比的比值等于2,比例的内项是0.08和0.6,这个比例是(
).
9、填空.
在比例里,(
)和(
)是外项;在里,(
)和(
)是内项.
10、如果4m=5n,那么m︰n=(
)
11、在一个比例里,两个内项互为倒数,其中一个外项是10以内既是奇数又是合数的数,则另一个外项是________.
12、一个长方形的周长是260cm,如果它的长减少,宽增加,就得到一个周长相等的长方形.原来长方形的面积是多少平方厘米?
13、把a×b=c×d(a,b,c,d均不为0)改写成比例式,你可以写出几个?
14、两个比的比值都是,它们组成的比例的外项分别是和,写出这个比例.
15、在12、8、16中添上一个数组成比例,这样的数你能写出几个?把可以组成的比例写出来(每个数写一个比例).
16、根据比例的基本性质,把下面的等积式改成比例式.
(1)3.6×5=2×9
(2)
17、应用比例的基本性质,判断下面各组中的两个比能否组成比例.
(1)5︰7和8︰13
(2)和
(3)和
(4)2.4︰5和4.8︰10
18、应用比例内项的积与外项的积的关系,判断下面哪几组的两个比可以组成比例,并写出组成的比例.
(1)2.8︰4和7︰10
_____________________________________________________
(2)2.7︰8和
_________________________________________
(3)3︰0.5和21︰3.5
________________________________________
19、奇思5分跑了1500m,妙想8分跑了2400m.
(1)奇思跑步的路程和时间的比是(
)︰(
).
(2)妙想跑步的路程和时间的比是(
)︰(
).
(3)这两个比能组成比例吗?为什么?如果能组成比例,请在下面写出比例.
20、把能组成比例的两个比连起来.
0.8︰3.2
5︰8
2.5︰4
10︰4
4.5︰18
21、
(1)分别写出上图中两个平行四边形底与底的比和高与高的比,判断这两个比能否组成比例.
(2)分别写出上图中每个平行四边形底与高的比,判断这两个比能否组成比例.
22、把8,40和32再配上一个数组成比例.
(1)把8和40同时作为外项(或内项),再配上(
)可以组成比例.
(2)把40和32同时作为外项(或内项),再配上(
)可以组成比例.
23、判断下列各组中的四个数能否组成比例,如果能,把组成的比例写下来.
(1)4,20,5和1(
)
__________________________________________________
(2)3,8,40和15(
)
___________________________________________
(3)2,0.6,5和2.5(
)
_________________________________________
(4),,30和24(
)
24、判断下面各组中的两个比能否组成比例,如果能,请写出来.
(1)4︰5和
(2)4.5︰1.5和
25、填空.
在比例中,(
)和(
)是外项;
在中,(
)和(
)是内项.
26、一根绳子,先用去40m,又用去余下长度的,这时余下的绳子正好是原来总长度的.求绳子原来长多少米.
27、学校体育室有排球、足球共48只,当排球借出,足球借出时,余下的排球与足球一样多.原来排球、足球各有多少只?
28、在括号里填上合适的数,便比例成立.
(1)8︰6=4.6︰(
)
(2)3.5︰(
)=1.4︰2
(3)
(4)
(5)
(6)
29、根据比例的基本性质,判断下面各表中相对应的两个量的比能否组成比例,如果能,把组成的比例写出来.
30、下面哪几组的两个比可以组成比例?把组成的比例写出来.
(1)6︰10和9︰15
(2)0.6︰0.2和
(3)1.5︰2和
(4)和
答案
1、(1)B(2)C(3)③(4)②(5)①(6)①(7)B
2、不成比例关系.因为边长×边长×块数=所铺正方形地面的面积.
3、(1)两个比相等
(2)0.75
0.75
相等
18:24=6:8
(3)略
4、(1)×
(2)×
5、(1)能
(2)1:4
不能
6、(1)5:10
20:40
5:10=20:40(2)25:100
不能
7、(1)4.5和6是外项,2.7和10是内项
(2)x和75是外项,1.2和25是内项
8、(1)相等(2)8,8,(3)外项,内项(4)0.16:0.08=0.6:0.3
9、
0.6
2
18
10、4︰5.
11、
12、长×=宽×
长:宽=:=8:5
面积:(×)×(×)=4000(cm)
13、8个,分别是a:c=d:b
b:c=d:a
c:a=b:d
d:a=b:c
a:d=c:b
b:d=c:a
c:b=a:d
d:b=a:c
14、=
15、3个,分别是6,24,.12:16=6:8
12:8=24:16
8:=12:16(所写比例不唯一)
16、(1)(答案不唯一)
(2)4:5=(答案不唯一)
17、(1)不能(2)能(3)能(4)能
18、(1)能组成比例,2.8︰4=7︰10,7︰10=2.8︰4
(2)不能组成比例
(3)能组成比例,3︰0.5=21︰3.5,21︰3.5=3︰0.5
19、(1)1500,5
(2)2400,8
(3)能组成比例,因为它们的比值相等.1500︰5=2400︰8,2400︰8=1500︰5
20、把能组成比例的两个比连起来.
0.8︰3.2
5︰8
2.5︰4
10︰4
4.5︰18
21、(1)底的比:4:8,高的比:2:4;两个平行四边形底的比值,高的比值都是,这两个比能组成比例,即4:8=2:4;
(2)左图中底:高=4:2,右图中底:高=8:4,每个平行四边形底与高的比值都是2,这两个比能组成比例,即4:2=8:4
22、(1)10
(2)160
23、(1)
能
20:4=5:1(所写比例不唯一)
(2)
能
40:8=15:3(所写比例不唯一)
(3)不能
(4)能
=24:30(所写比例不唯一)
24、(1)能
4:5=
(2)能
4.5:1.5=
25、,0.6,2,18
26、因为第一次余下长度×(1-)=原来总长度×,
所以第一次余下长度:原来总长度=:(1-)=5:9
绳子原来长:40÷(1-)=90(m)
27、因为排球×(1-)=足球×(1-),
所以排球:足球=:=3:5
排球:48×=18(只)
足球:48-18=30(只)
28、(1)3.45(2)5(3)(4)2.4
(5)(6)
29、能
210:3=560:8
能
11:27.5=16:40
不能
30、(1)能,6:10=9:15(2)能,(3)不能(4)能
