六年级数学下册试题 一课一练4.2《正比例》习题1-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练4.2《正比例》习题1-北师大版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 361.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 16:15:07 | ||
图片预览





文档简介
4.2《正比例》习题1
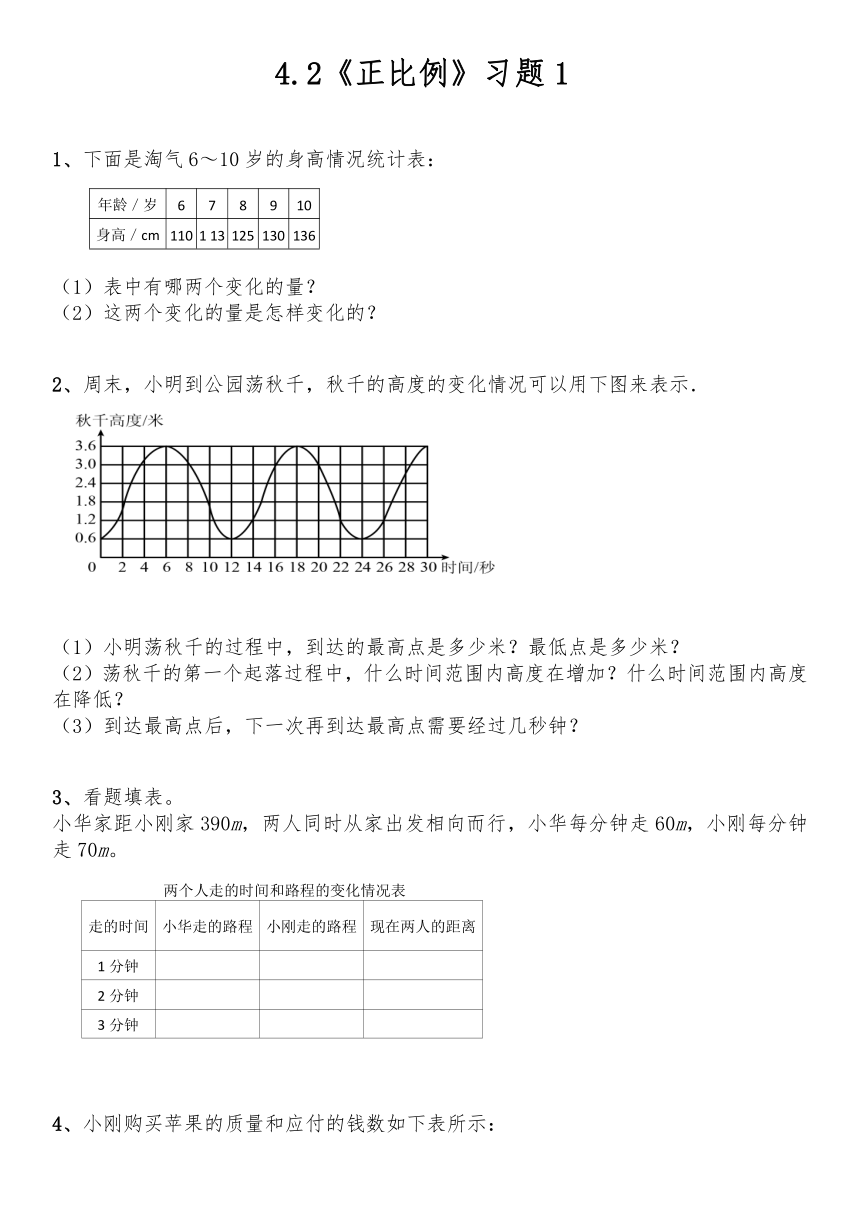
1、下面是淘气6~10岁的身高情况统计表:
(1)表中有哪两个变化的量?
(2)这两个变化的量是怎样变化的?
2、周末,小明到公园荡秋千,秋千的高度的变化情况可以用下图来表示.
(1)小明荡秋千的过程中,到达的最高点是多少米?最低点是多少米?
(2)荡秋千的第一个起落过程中,什么时间范围内高度在增加?什么时间范围内高度在降低?
(3)到达最高点后,下一次再到达最高点需要经过几秒钟?
3、看题填表。
小华家距小刚家390m,两人同时从家出发相向而行,小华每分钟走60m,小刚每分钟走70m。
4、小刚购买苹果的质量和应付的钱数如下表所示:
(1)表中购买苹果的质量和应付的钱数是如何变化的?
(2)用a(a>0)表示购买苹果的质量,用b表示应付的钱数,用式子表示出购买苹果的质量a与应付的钱数b之间的关系.
5、小红看《水浒传》的时间和页数如下表:
表中(
)和(
)在发生变化,(
)随着(
)的变化而变化.时间越多,所看的页数就越(
);反之,时间越少,所看的页数就越(
).
6、科学课后,笑笑观察了学校旗杆影子长度与时间的关系,制成下表:
笑笑由此总结:影子会越来越短,也就是从日出到日落,旗杆影子由长变短.她的总结对吗?为什么?
7、小明今年8岁,妈妈36岁,根据这个信息把下表填写完整.
(1)表中(
)与(
)在发生变化,(
)不变.
(2)如果用x表示妈妈的年龄,用y表示小明的年龄,那么小明的年龄和妈妈的年龄的关系表示为(
).
8、如果x=6y(y≠0),那么x和y成(
)比例关系.
9、填空.
(1)为提高自身的阅读能力,学生们积极订阅书刊,认真阅读.某书店销售《小学生天地》的份数和总价如下表:
①表中(
)和(
)是相关联的量,(
)增加,(
)也随着增加.
②总价与份数这两个相关联的量中相对应的两个数的比值都是(
),这个比值实际上是(
).
③因为总价与份数的比值一定,所以表中的两种量叫做成(
)的量.
(2)路程与时间的比值是(
),当这个比值一定时,(
)和(
)成(
)比例关系.
10、下面是王奶奶家去年下半年每月用水的水费情况.
(1)分别写出各月水费与用水量的比,比较比值的大小.
(2)这个比值表示的意义是什么?
(3)水费与相对应的用水量成正比例关系吗?为什么?
11、看表填一填.
(
)和(
)是两个变化的量,变化的规律是(
),路程和时间成(
)比例.
12、填空.
已知x和y是正比例关系,根据表中条件,填写下表.
13、填一填.
(1)乘船的人数与所付船费如下表.
①表格中的(
)和(
)是两种相关联的量,船费随着(
)的变化而变化.
②船费与人数两种量中相对应的两个数的比值是(
),这个比值实际上是(
).
③因为每人的(
)一定,所以(
)和(
)成(
)比例关系.
(2)两种相关联的量,一种量变化,另一种量也随着(
),如果这两种量中(
)的两个数的(
)一定,这两种量就叫做成正比例关系的量.
(3)如果用x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为(
).
(4)因为(一定),所以总价和数量成(
)比例关系.
(5)因为(一定),所以(
)和(
)成(
)比例关系.
14、选择.(将正确答案的字母填在括号里)
(1)下列各组中两种量不成正比例关系的是(
).
A.人的身高与年龄
B.y=5x,y和x
C.工作效率一定,工作总量和工作时间
D.圆的周长与直径
(2)甲数的与乙数的相等(甲、乙均不为0),甲数与乙数(
).
A.成正比例关系
B.不成正比例关系
C.无法判断
15、下表中关于正方体的一些数量,哪两种量成正比例关系?说明理由.
16、下面是6位同学家4月份的用电情况.
(1)根据表中的数据找规律,把上表填写完整.
(2)表中变化的量有几种?它们的变化规律是什么?
(3)写出表中给出的已知的相关联两种量的比值,并说说比值表示什么?
(4)表中的两种相关联的量成正比例关系吗?为什么?
17、在下面成正比例关系的两个量的后面画“√”.
(1)平行四边形的底一定,它的面积与高.(
)
(2)汽车行驶的速度一定,行驶的路程与时间.(
)
(3)正方形的面积和边长.(
)
(4)订阅《英语报》的份数和总钱数.(
)
(5)圆的周长和它的半径.(
)
(6)4A=12B(A、B均不为0),A和B.(
)
(7)圆的半径和它的面积.(
)
(8)李玲的体重与她的身高.(
)
18、判断下面各题中的两个量是否成正比例,并说明理由.
(1)汽车行驶的速度一定,行驶的路程与时间.
(2)一本书的页数一定,看了的页数与剩下的页数.
(3)小明的年龄和体重.
19、购买甲、乙两种练习本的数量和总价的变化情况如下图所示.
(1)两种练习本各买5本,分别需要多少元?
(2)从图上看,哪种练习本便宜些?
20、甲、乙两车行驶的路程和时间的关系如下图.
(1)从图中可以看出,甲车行驶的路程与行驶的时间成什么比例关系?乙车呢?
(2)如果甲、乙两车从A.B两地同时出发,相向而行,经过5小时相遇,A.B两地相距多少千米?
21、购买《典中点》的本数与总价的情况如下表.
(1)把上面的表格填写完整.
(2)根据表中数据,在下图中描出购买《典中点》的总价和数量所对应的点,再把这些点依次连起来.
(3)购买《典中点》的总价和数量成正比例关系吗?为什么?
22、张大伯从厂家进了一批不同的商品,现在全部按进价的200%出售.
(1)填表.
(2)完成下图.
(3)如果用戈x示进价,用y表示售价,那么y=________.
(4)售价与进价是否成正比例?为什么?
答案
1、(1)表中有年龄和身高这两个变化的量.
(2)身高随着年龄的增长而增长.
2、(1)最高点:3.6米;最低点:0.6米(2)0~6秒;6~12秒(3)12秒
3、60m,70m,260m,120m,140m,130m,180m,210m,0m
4、(1)应付的钱数随购买苹果的质量的增加而增加.
(2)=4
5、时间,页数,页数,时间,多,少
6、不对,因为从早晨到中午,旗杆影子逐渐变短;从中午到傍晚,旗杆影子逐渐变长.
7、29;31;33;40;48;53(1)小明的年龄;妈妈的年龄;年龄差(2)y=x-28
8、正
9、(1)①份数
总价
份数
总价
②
30
《小学生天地》的单价
③正比例
(2)速度
路程
时间
正
10、(1)
(2)比值2.8表示每吨水的价钱
(3)成正比例关系.因为水费相对应的用水量的比值一定.
11、时间,路程,路程和时间的比值一定,正
12、
13、(1)①人数船费人数②5
每人付的船费③船费船费人数正
(2)变化相对应比值
(3)(一定)
(4)单价正
(5)工作总量工作时间工作总量
14、(1)A(2)A
15、正方体的表面积和底面积成正比例关系.
因为:表面积÷底面积=6.
正方体的质量与体积成正比例关系.
因为:质量÷体积=每立方厘米的质量(一定).
16、(1)冉庄家:15.95
小红家:16.5
小立家:17.6
(2)表中变化的量有:用电量(单位:千瓦时)和电费(单位:元)两种相关联的量,它们的变化规律是:电费随着用电量的增加而增加.
(3)=0.55
=0.55
=0.55,它们的比值表示每千瓦时电的价格
(4)表中两种相关联的量成正比例关系.
因为=每千瓦时电的价格(一定),
所以电费和用电量成正比例关系
17、(1)√(2)√(3)(4)√(5)√(6)√(7)(8)
18、(1)成正比例;(一定)(2)不成正比例;看了的页数+剩下的页数=一本的页数(一定),但比值不一定(3)不成正比例;年龄和体重是两种不相关联的量
19、(1)从题图中可以看出,甲种练习本的单价是2元,乙种练习本的单价是1元,
甲种练习本:2×5=10(元)
乙种练习本:1×5=5(元)
两种练习本各买5本,分别需要10元和5元.
(2)从题图中来看,数量相同的情况下,乙种练习本的总价少一些,所以乙种练习本便宜些.
20、(1)因为=速度(一定),
所以甲车行驶的路程与行驶的时间成正比例关系.
同理,乙车行驶的路程与行驶的时间成正比例关系.
点拨:甲车1小时行90km,2小时行180km……,==…=60.
(2)甲车速度:=90(千米/时)
乙车速度:=60(千米/时)
(90+60)×5=750(km)
21、(1)
数量/本
1
2
3
5
7
总价/元
17.9
35.8
53.7
89.5
125.3
(2)
(3)成正比例关系.因为=单价(一定),
所以购买《典中点》的总价和数量成正比例关系.
22、(1)
(2)
(3)200%x
(4)售价与进价成正比例,因为=200%(一定)
1、下面是淘气6~10岁的身高情况统计表:
(1)表中有哪两个变化的量?
(2)这两个变化的量是怎样变化的?
2、周末,小明到公园荡秋千,秋千的高度的变化情况可以用下图来表示.
(1)小明荡秋千的过程中,到达的最高点是多少米?最低点是多少米?
(2)荡秋千的第一个起落过程中,什么时间范围内高度在增加?什么时间范围内高度在降低?
(3)到达最高点后,下一次再到达最高点需要经过几秒钟?
3、看题填表。
小华家距小刚家390m,两人同时从家出发相向而行,小华每分钟走60m,小刚每分钟走70m。
4、小刚购买苹果的质量和应付的钱数如下表所示:
(1)表中购买苹果的质量和应付的钱数是如何变化的?
(2)用a(a>0)表示购买苹果的质量,用b表示应付的钱数,用式子表示出购买苹果的质量a与应付的钱数b之间的关系.
5、小红看《水浒传》的时间和页数如下表:
表中(
)和(
)在发生变化,(
)随着(
)的变化而变化.时间越多,所看的页数就越(
);反之,时间越少,所看的页数就越(
).
6、科学课后,笑笑观察了学校旗杆影子长度与时间的关系,制成下表:
笑笑由此总结:影子会越来越短,也就是从日出到日落,旗杆影子由长变短.她的总结对吗?为什么?
7、小明今年8岁,妈妈36岁,根据这个信息把下表填写完整.
(1)表中(
)与(
)在发生变化,(
)不变.
(2)如果用x表示妈妈的年龄,用y表示小明的年龄,那么小明的年龄和妈妈的年龄的关系表示为(
).
8、如果x=6y(y≠0),那么x和y成(
)比例关系.
9、填空.
(1)为提高自身的阅读能力,学生们积极订阅书刊,认真阅读.某书店销售《小学生天地》的份数和总价如下表:
①表中(
)和(
)是相关联的量,(
)增加,(
)也随着增加.
②总价与份数这两个相关联的量中相对应的两个数的比值都是(
),这个比值实际上是(
).
③因为总价与份数的比值一定,所以表中的两种量叫做成(
)的量.
(2)路程与时间的比值是(
),当这个比值一定时,(
)和(
)成(
)比例关系.
10、下面是王奶奶家去年下半年每月用水的水费情况.
(1)分别写出各月水费与用水量的比,比较比值的大小.
(2)这个比值表示的意义是什么?
(3)水费与相对应的用水量成正比例关系吗?为什么?
11、看表填一填.
(
)和(
)是两个变化的量,变化的规律是(
),路程和时间成(
)比例.
12、填空.
已知x和y是正比例关系,根据表中条件,填写下表.
13、填一填.
(1)乘船的人数与所付船费如下表.
①表格中的(
)和(
)是两种相关联的量,船费随着(
)的变化而变化.
②船费与人数两种量中相对应的两个数的比值是(
),这个比值实际上是(
).
③因为每人的(
)一定,所以(
)和(
)成(
)比例关系.
(2)两种相关联的量,一种量变化,另一种量也随着(
),如果这两种量中(
)的两个数的(
)一定,这两种量就叫做成正比例关系的量.
(3)如果用x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为(
).
(4)因为(一定),所以总价和数量成(
)比例关系.
(5)因为(一定),所以(
)和(
)成(
)比例关系.
14、选择.(将正确答案的字母填在括号里)
(1)下列各组中两种量不成正比例关系的是(
).
A.人的身高与年龄
B.y=5x,y和x
C.工作效率一定,工作总量和工作时间
D.圆的周长与直径
(2)甲数的与乙数的相等(甲、乙均不为0),甲数与乙数(
).
A.成正比例关系
B.不成正比例关系
C.无法判断
15、下表中关于正方体的一些数量,哪两种量成正比例关系?说明理由.
16、下面是6位同学家4月份的用电情况.
(1)根据表中的数据找规律,把上表填写完整.
(2)表中变化的量有几种?它们的变化规律是什么?
(3)写出表中给出的已知的相关联两种量的比值,并说说比值表示什么?
(4)表中的两种相关联的量成正比例关系吗?为什么?
17、在下面成正比例关系的两个量的后面画“√”.
(1)平行四边形的底一定,它的面积与高.(
)
(2)汽车行驶的速度一定,行驶的路程与时间.(
)
(3)正方形的面积和边长.(
)
(4)订阅《英语报》的份数和总钱数.(
)
(5)圆的周长和它的半径.(
)
(6)4A=12B(A、B均不为0),A和B.(
)
(7)圆的半径和它的面积.(
)
(8)李玲的体重与她的身高.(
)
18、判断下面各题中的两个量是否成正比例,并说明理由.
(1)汽车行驶的速度一定,行驶的路程与时间.
(2)一本书的页数一定,看了的页数与剩下的页数.
(3)小明的年龄和体重.
19、购买甲、乙两种练习本的数量和总价的变化情况如下图所示.
(1)两种练习本各买5本,分别需要多少元?
(2)从图上看,哪种练习本便宜些?
20、甲、乙两车行驶的路程和时间的关系如下图.
(1)从图中可以看出,甲车行驶的路程与行驶的时间成什么比例关系?乙车呢?
(2)如果甲、乙两车从A.B两地同时出发,相向而行,经过5小时相遇,A.B两地相距多少千米?
21、购买《典中点》的本数与总价的情况如下表.
(1)把上面的表格填写完整.
(2)根据表中数据,在下图中描出购买《典中点》的总价和数量所对应的点,再把这些点依次连起来.
(3)购买《典中点》的总价和数量成正比例关系吗?为什么?
22、张大伯从厂家进了一批不同的商品,现在全部按进价的200%出售.
(1)填表.
(2)完成下图.
(3)如果用戈x示进价,用y表示售价,那么y=________.
(4)售价与进价是否成正比例?为什么?
答案
1、(1)表中有年龄和身高这两个变化的量.
(2)身高随着年龄的增长而增长.
2、(1)最高点:3.6米;最低点:0.6米(2)0~6秒;6~12秒(3)12秒
3、60m,70m,260m,120m,140m,130m,180m,210m,0m
4、(1)应付的钱数随购买苹果的质量的增加而增加.
(2)=4
5、时间,页数,页数,时间,多,少
6、不对,因为从早晨到中午,旗杆影子逐渐变短;从中午到傍晚,旗杆影子逐渐变长.
7、29;31;33;40;48;53(1)小明的年龄;妈妈的年龄;年龄差(2)y=x-28
8、正
9、(1)①份数
总价
份数
总价
②
30
《小学生天地》的单价
③正比例
(2)速度
路程
时间
正
10、(1)
(2)比值2.8表示每吨水的价钱
(3)成正比例关系.因为水费相对应的用水量的比值一定.
11、时间,路程,路程和时间的比值一定,正
12、
13、(1)①人数船费人数②5
每人付的船费③船费船费人数正
(2)变化相对应比值
(3)(一定)
(4)单价正
(5)工作总量工作时间工作总量
14、(1)A(2)A
15、正方体的表面积和底面积成正比例关系.
因为:表面积÷底面积=6.
正方体的质量与体积成正比例关系.
因为:质量÷体积=每立方厘米的质量(一定).
16、(1)冉庄家:15.95
小红家:16.5
小立家:17.6
(2)表中变化的量有:用电量(单位:千瓦时)和电费(单位:元)两种相关联的量,它们的变化规律是:电费随着用电量的增加而增加.
(3)=0.55
=0.55
=0.55,它们的比值表示每千瓦时电的价格
(4)表中两种相关联的量成正比例关系.
因为=每千瓦时电的价格(一定),
所以电费和用电量成正比例关系
17、(1)√(2)√(3)(4)√(5)√(6)√(7)(8)
18、(1)成正比例;(一定)(2)不成正比例;看了的页数+剩下的页数=一本的页数(一定),但比值不一定(3)不成正比例;年龄和体重是两种不相关联的量
19、(1)从题图中可以看出,甲种练习本的单价是2元,乙种练习本的单价是1元,
甲种练习本:2×5=10(元)
乙种练习本:1×5=5(元)
两种练习本各买5本,分别需要10元和5元.
(2)从题图中来看,数量相同的情况下,乙种练习本的总价少一些,所以乙种练习本便宜些.
20、(1)因为=速度(一定),
所以甲车行驶的路程与行驶的时间成正比例关系.
同理,乙车行驶的路程与行驶的时间成正比例关系.
点拨:甲车1小时行90km,2小时行180km……,==…=60.
(2)甲车速度:=90(千米/时)
乙车速度:=60(千米/时)
(90+60)×5=750(km)
21、(1)
数量/本
1
2
3
5
7
总价/元
17.9
35.8
53.7
89.5
125.3
(2)
(3)成正比例关系.因为=单价(一定),
所以购买《典中点》的总价和数量成正比例关系.
22、(1)
(2)
(3)200%x
(4)售价与进价成正比例,因为=200%(一定)
