2020-2021学年苏科版七年级数学下册《9.4乘法公式》课后优生辅导提升训练(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册《9.4乘法公式》课后优生辅导提升训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 101.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 19:37:36 | ||
图片预览



文档简介
2021年度苏科版七年级数学下册《9.4乘法公式》课后优生辅导提升训练(附答案)
1.如图,将图①中大小相同的四个小正方形按图②所示的方式放置变为一个大正方形,根据两个图形中阴影部分的面积关系,可以验证(
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab D.(a+b)(a﹣b)=a2﹣b2
2.若a2﹣b2=16,(a+b)2=8,则ab的值为( )
A.﹣ B. C.﹣6 D.6
3.已知x﹣y=3,xy=3,则(x+y)2的值为( )
A.24 B.18 C.21 D.12
4.已知4a2+12ab+m是一个完全平方式,那么m为( )
A.3b2 B.b2 C.9b2 D.36b2
5.设x,y是实数,定义“※”的一种运算如下:x※y=(x﹣y)2,则下列结论:①若x※y=0,则x=0或y=0;②x※y=y※x;③(x﹣y)※(y﹣z)=x※(﹣z);④x※(y+z)=x※y+y※z+x※(﹣z);其中正确的有( )个.
A.1 B.2 C.3 D.4
6.如果(a+b)2=16,(a﹣b)2=4,且a、b是长方形的长和宽,则这个长方形的面积是( )
A.3 B.4 C.5 D.6
7.若s﹣t=7,则s2﹣t2﹣14t的值是( )
A.42 B.50 C.56 D.49
8.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x) B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y) D.(x﹣y)(﹣x+y)
9.已知m2+n2=15,(m﹣n)2=1,则(m+n)2= .
10.若a+b=9,ab=14,则a﹣b= .
11.已知x﹣y=2,x+y=﹣4,则x2﹣y2= .
12.计算(x+2y﹣z)(x﹣2y+z)= .
13.化简(2x﹣3)2﹣(x+y)(x﹣y)﹣y2= .
14.已知a+b=﹣6,ab=10,则a2﹣ab+b2= .
15.若x2+2(m﹣3)x+9是完全平方式,则m的值等于 .
16.计算:(a﹣1)2?(a+1)2= .
17.计算:(3﹣2t)(﹣3﹣2t)= .
18.如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是 .
19.二次三项式4x2﹣(k﹣5)x+9是完全平方式,则k的值是 .
20.设(2a+3b)2=(2a﹣3b)2+A,则A= .
21.计算:2019×2021﹣20202= .
22.观察下列各式:
1﹣=1﹣==×;
1﹣=1﹣==×;
1﹣=1﹣==×;
1﹣=1﹣==×;
…
(1)用你发现的规律填空:1﹣= × ,1﹣= × ;
(2)用你发现的规律进行计算:
(1﹣)×(1﹣)×(1﹣)×…×(1﹣)×(1﹣).
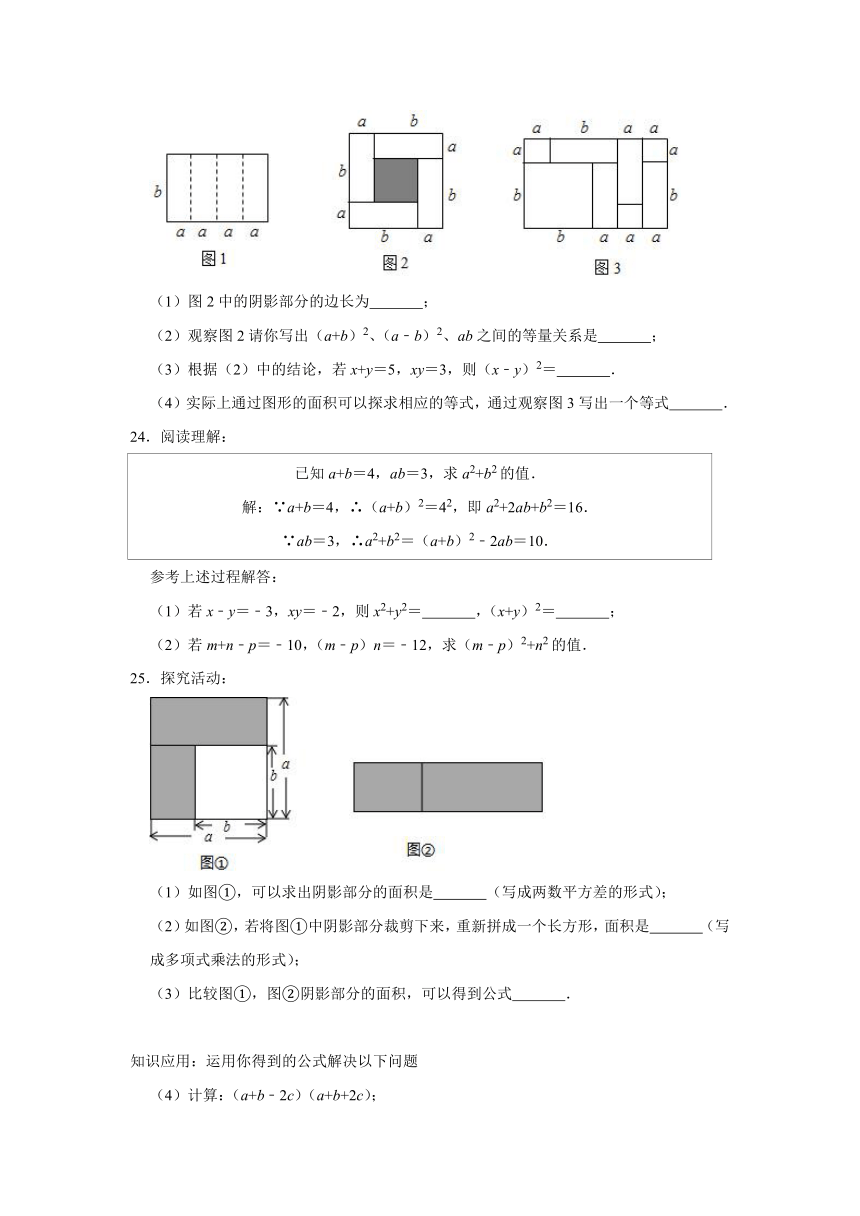
23.如图1,是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中的阴影部分的边长为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=5,xy=3,则(x﹣y)2= .
(4)实际上通过图形的面积可以探求相应的等式,通过观察图3写出一个等式 .
24.阅读理解:
已知a+b=4,ab=3,求a2+b2的值. 解:∵a+b=4,∴(a+b)2=42,即a2+2ab+b2=16.
∵ab=3,∴a2+b2=(a+b)2﹣2ab=10.
参考上述过程解答:
(1)若x﹣y=﹣3,xy=﹣2,则x2+y2= ,(x+y)2= ;
(2)若m+n﹣p=﹣10,(m﹣p)n=﹣12,求(m﹣p)2+n2的值.
25.探究活动:
(1)如图①,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图②,若将图①中阴影部分裁剪下来,重新拼成一个长方形,面积是 (写成多项式乘法的形式);
(3)比较图①,图②阴影部分的面积,可以得到公式 .
知识应用:运用你得到的公式解决以下问题
(4)计算:(a+b﹣2c)(a+b+2c);
(5)若4x2﹣9y2=10,4x+6y=4,求2x﹣3y的值.
26.先化简,再求值:(2x﹣y)2﹣(x﹣3y)(x+3y)+4(xy﹣y2),其中x=﹣2,y=1.
27.已知(a+b)2=25,(a﹣b)2=9.求a2﹣6ab+b2.
参考答案
1.解:阴影部分的面积是四个阴影小正方形的面积和,由拼图可得四个阴影小正方形可以拼成边长为(a﹣b)的正方形,因此面积为(a﹣b)2,
由图2可知,阴影部分的面积等于边长为a的正方形的面积减去之间十字架的面积,即:a2﹣2ab+b2,
因此有(a﹣b)2=a2﹣2ab+b2,故选:A.
2.解:∵a2﹣b2=16,
∴(a+b)(a﹣b)=16,
∴(a+b)2(a﹣b)2=256,
∵(a+b)2=8,
∴(a﹣b)2=32,
∴ab===﹣6,故选:C.
3.解:∵x﹣y=3,xy=3,
∴(x+y)2=(x﹣y)2+4xy=32+4×3=21,故选:C.
4.解:∵4a2+12ab+m是一个完全平方式,∴m=9b2.故选:C.
5.解:①若x※y=(x﹣y)2=0,则x=y,原来的说法错误;
②∵x※y=(x﹣y)2,y※x=(y﹣x)2=(x﹣y)2,∴x※y=y※x是正确的;
③(x﹣y)※(y﹣z)=[(x﹣y)﹣(y﹣z)]2=(x﹣2y+z)2,x※(﹣z)=(x+z)2,则(x﹣y)※(y﹣z)≠x※(﹣z),原来的说法错误;
④∵x※(y+z)=(x﹣y﹣z)2,x※y+y※z+x※(﹣z)=(x﹣y)2+(y﹣z)2+(x+z)2,则x※(y+z)≠x※y+y※z+x※(﹣z),原来的说法错误.
故其中正确的有1个.故选:A.
6.解:∵(a+b)2=16,(a﹣b)2=4,
∴(a+b)2﹣(a﹣b)2=4ab=12,
∴ab=3,
∴长方形的面积为3,故选:A.
7.解:∵s﹣t=7,
∴s2﹣t2﹣14t=(s+t)(s﹣t)﹣14t=7(s+t)﹣14t=7s+7t﹣14t
=7s﹣7t=7(s﹣t)=7×7=49.故选:D.
8.解:A、(2x+y)(2y﹣x),不能用平方差公式进行计算,故本选项不符合题意;
B、(x+1)(﹣x﹣1),不能用平方差公式进行计算,故本选项不符合题意;
C、(3x﹣y)(3x+y),能用平方差公式进行计算,故本选项符合题意;
D、(x﹣y)(﹣x+y)不能用平方差公式进行计算,故本选项不符合题意;
故选:C.
9.解:因为m2+n2=15,(m﹣n)2=1,
所以m2+n2﹣(m﹣n)2=2mn=15﹣1=14,
所以(m+n)2=m2+n2+2mn=15+14=29.
故答案为:29.
10.解:∵a+b=9,ab=14,
∴(a﹣b)2=(a+b)2﹣4ab=92﹣4×14=81﹣56=25,
∴a﹣b=±5.
故答案为:±5.
11.解:∵x﹣y=2,x+y=﹣4,
∴x2﹣y2=(x﹣y)(x+y)=2×(﹣4)=﹣8.
故答案为:﹣8.
12.解:(x+2y﹣z)(x﹣2y+z)=x2﹣(2y﹣z)2=x2﹣4y2+4yz﹣z2.
故答案是:x2﹣4y2+4yz﹣z2.
13.解:原式=(4x2﹣12x+9)﹣(x2﹣y2)﹣y2=4x2﹣12x+9﹣x2+y2﹣y2=3x2﹣12x+9.
故答案为:3x2﹣12x+9.
14.解:∵a+b=﹣6,ab=10,
∴a2﹣ab+b2=(a+b)2﹣3ab=(﹣6)2﹣3×10=36﹣30=6.
故答案为:6.
15.解:∵x2+2(m﹣3)x+9是完全平方式,
∴m﹣3=±3,
解得:m=6或0.
故答案为:6或0.
16.解:(a﹣1)2?(a+1)2=[(a﹣1)(a+1)]2=(a2﹣1)2=a4﹣2a2+1.
故答案为:a4﹣2a2+1.
17.解:原式=(﹣2t+3)(﹣2t﹣3)=(﹣2t)2﹣32=4t2﹣9,故答案为:4t2﹣9.
18.解:设大正方形的边长为a,小正方形的边长为b,
故阴影部分的面积是:AE?BC+AE?BD=AE(BC+BD)
=(AB﹣BE)(BC+BD)=(a﹣b)(a+b)=(a2﹣b2)=×60=30.
故答案为:30.
19.解:∵二次三项式4x2﹣(k﹣5)x+9是完全平方式,
∴k﹣5=±12,
解得:k=17或k=﹣7.
故答案为:17或﹣7.
20.解:∵(2a+3b)2=4a2+12ab+9b2,
(2a﹣3b)2=4a2﹣12ab+9b2,
∴(2a+3b)2=(2a﹣3b)2+24ab,
∴A=24ab,
故答案为:24ab.
21.解:2019×2021﹣20202
=(2000﹣1)×(2000+1)﹣20202=20202﹣1﹣20202=﹣1.
故答案为:﹣1.
22.解:(1)1﹣=(1﹣)×(1+)=,
1﹣=(1﹣)×(1+)=,
故答案为:,,,;
(2)原式=××××××…××××=×
=.
23.解:(1)由图象可知:阴影部分的边长为b﹣a,
故答案为:b﹣a;
(2)由图可知,图1的面积为4ab,图2中白色部分的面积为(a+b)2﹣(b﹣a)2=(a+b)2﹣(a﹣b)2,
∵图1的面积和图2中白色部分的面积相等,
∴(a+b)2﹣(a﹣b)2=4ab,
故答案为:(a+b)2﹣(a﹣b)2=4ab;
(3)根据(1)中的结论,可知(x+y)2﹣(x﹣y)2=4xy,
∵x+y=5,x?y=3,
∴52﹣(x﹣y)2=4×3,
∴(x﹣y)2=13,
故答案为:13;
(4)由图可得,长方形的面积=(a+b)(3a+b),
长方形的面积=3a2+4ab+b2,
∴(a+b)(3a+b)=3a2+4ab+b2.
故答案为:(a+b)(3a+b)=3a2+4ab+b2.
24.解:(1)∵x﹣y=﹣3,xy=﹣2,
∴x2+y2=(x﹣y)2+2xy=9﹣4=5,
∴(x+y)2=x2+2xy+y2=5﹣4=1,
故答案为:5,1;
(2)∵m+n﹣p=﹣10,(m﹣p)n=﹣12,
∴(m﹣p)2+n2=(m﹣p+n)2﹣2(m﹣p)n=100+24=124.
25.解:(1)S阴影部分=S大正方形﹣S小正方形=a2﹣b2,
故答案为:a2﹣b2;
(2)拼成的长方形的长为(a+b),宽为(a﹣b),
所以S阴影部分=S长方形=(a+b)(a﹣b),
故答案为:(a+b)(a﹣b);
(3)由(1)、(2)可得,a2﹣b2=(a+b)(a﹣b);
故答案为:a2﹣b2=(a+b)(a﹣b);
(4)原式=[(a+b)﹣2c][(a+b)+2c]=(a+b)2﹣(2c)2,
=a2+2ab+b2﹣4c2;
(5)∵4x2﹣9y2=(2x+3y)(2x﹣3y)=10,
4x+6y=4,
∴2x+3y=2,
∴2x﹣3y=10÷2=5,
故2x﹣3y的值为5.
26.解:原式=4x2+y2﹣4xy﹣(x2﹣9y2)+4xy﹣4y2
=4x2+y2﹣4xy﹣x2+9y2+4xy﹣4y2=3x2+6y2,
当x=﹣2,y=1时,
原式=3×(﹣2)2+6×12=12+6
=18.
27.解:因为(a+b)2=25,(a﹣b)2=9,
所以(a+b)2﹣(a﹣b)2=4ab=16,
所以a2﹣6ab+b2=(a﹣b)2﹣4ab=9﹣16=﹣7
1.如图,将图①中大小相同的四个小正方形按图②所示的方式放置变为一个大正方形,根据两个图形中阴影部分的面积关系,可以验证(
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab D.(a+b)(a﹣b)=a2﹣b2
2.若a2﹣b2=16,(a+b)2=8,则ab的值为( )
A.﹣ B. C.﹣6 D.6
3.已知x﹣y=3,xy=3,则(x+y)2的值为( )
A.24 B.18 C.21 D.12
4.已知4a2+12ab+m是一个完全平方式,那么m为( )
A.3b2 B.b2 C.9b2 D.36b2
5.设x,y是实数,定义“※”的一种运算如下:x※y=(x﹣y)2,则下列结论:①若x※y=0,则x=0或y=0;②x※y=y※x;③(x﹣y)※(y﹣z)=x※(﹣z);④x※(y+z)=x※y+y※z+x※(﹣z);其中正确的有( )个.
A.1 B.2 C.3 D.4
6.如果(a+b)2=16,(a﹣b)2=4,且a、b是长方形的长和宽,则这个长方形的面积是( )
A.3 B.4 C.5 D.6
7.若s﹣t=7,则s2﹣t2﹣14t的值是( )
A.42 B.50 C.56 D.49
8.在下列多项式的乘法中,可以用平方差公式计算的是( )
A.(2x+y)(2y﹣x) B.(x+1)(﹣x﹣1)
C.(3x﹣y)(3x+y) D.(x﹣y)(﹣x+y)
9.已知m2+n2=15,(m﹣n)2=1,则(m+n)2= .
10.若a+b=9,ab=14,则a﹣b= .
11.已知x﹣y=2,x+y=﹣4,则x2﹣y2= .
12.计算(x+2y﹣z)(x﹣2y+z)= .
13.化简(2x﹣3)2﹣(x+y)(x﹣y)﹣y2= .
14.已知a+b=﹣6,ab=10,则a2﹣ab+b2= .
15.若x2+2(m﹣3)x+9是完全平方式,则m的值等于 .
16.计算:(a﹣1)2?(a+1)2= .
17.计算:(3﹣2t)(﹣3﹣2t)= .
18.如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是 .
19.二次三项式4x2﹣(k﹣5)x+9是完全平方式,则k的值是 .
20.设(2a+3b)2=(2a﹣3b)2+A,则A= .
21.计算:2019×2021﹣20202= .
22.观察下列各式:
1﹣=1﹣==×;
1﹣=1﹣==×;
1﹣=1﹣==×;
1﹣=1﹣==×;
…
(1)用你发现的规律填空:1﹣= × ,1﹣= × ;
(2)用你发现的规律进行计算:
(1﹣)×(1﹣)×(1﹣)×…×(1﹣)×(1﹣).
23.如图1,是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中的阴影部分的边长为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=5,xy=3,则(x﹣y)2= .
(4)实际上通过图形的面积可以探求相应的等式,通过观察图3写出一个等式 .
24.阅读理解:
已知a+b=4,ab=3,求a2+b2的值. 解:∵a+b=4,∴(a+b)2=42,即a2+2ab+b2=16.
∵ab=3,∴a2+b2=(a+b)2﹣2ab=10.
参考上述过程解答:
(1)若x﹣y=﹣3,xy=﹣2,则x2+y2= ,(x+y)2= ;
(2)若m+n﹣p=﹣10,(m﹣p)n=﹣12,求(m﹣p)2+n2的值.
25.探究活动:
(1)如图①,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图②,若将图①中阴影部分裁剪下来,重新拼成一个长方形,面积是 (写成多项式乘法的形式);
(3)比较图①,图②阴影部分的面积,可以得到公式 .
知识应用:运用你得到的公式解决以下问题
(4)计算:(a+b﹣2c)(a+b+2c);
(5)若4x2﹣9y2=10,4x+6y=4,求2x﹣3y的值.
26.先化简,再求值:(2x﹣y)2﹣(x﹣3y)(x+3y)+4(xy﹣y2),其中x=﹣2,y=1.
27.已知(a+b)2=25,(a﹣b)2=9.求a2﹣6ab+b2.
参考答案
1.解:阴影部分的面积是四个阴影小正方形的面积和,由拼图可得四个阴影小正方形可以拼成边长为(a﹣b)的正方形,因此面积为(a﹣b)2,
由图2可知,阴影部分的面积等于边长为a的正方形的面积减去之间十字架的面积,即:a2﹣2ab+b2,
因此有(a﹣b)2=a2﹣2ab+b2,故选:A.
2.解:∵a2﹣b2=16,
∴(a+b)(a﹣b)=16,
∴(a+b)2(a﹣b)2=256,
∵(a+b)2=8,
∴(a﹣b)2=32,
∴ab===﹣6,故选:C.
3.解:∵x﹣y=3,xy=3,
∴(x+y)2=(x﹣y)2+4xy=32+4×3=21,故选:C.
4.解:∵4a2+12ab+m是一个完全平方式,∴m=9b2.故选:C.
5.解:①若x※y=(x﹣y)2=0,则x=y,原来的说法错误;
②∵x※y=(x﹣y)2,y※x=(y﹣x)2=(x﹣y)2,∴x※y=y※x是正确的;
③(x﹣y)※(y﹣z)=[(x﹣y)﹣(y﹣z)]2=(x﹣2y+z)2,x※(﹣z)=(x+z)2,则(x﹣y)※(y﹣z)≠x※(﹣z),原来的说法错误;
④∵x※(y+z)=(x﹣y﹣z)2,x※y+y※z+x※(﹣z)=(x﹣y)2+(y﹣z)2+(x+z)2,则x※(y+z)≠x※y+y※z+x※(﹣z),原来的说法错误.
故其中正确的有1个.故选:A.
6.解:∵(a+b)2=16,(a﹣b)2=4,
∴(a+b)2﹣(a﹣b)2=4ab=12,
∴ab=3,
∴长方形的面积为3,故选:A.
7.解:∵s﹣t=7,
∴s2﹣t2﹣14t=(s+t)(s﹣t)﹣14t=7(s+t)﹣14t=7s+7t﹣14t
=7s﹣7t=7(s﹣t)=7×7=49.故选:D.
8.解:A、(2x+y)(2y﹣x),不能用平方差公式进行计算,故本选项不符合题意;
B、(x+1)(﹣x﹣1),不能用平方差公式进行计算,故本选项不符合题意;
C、(3x﹣y)(3x+y),能用平方差公式进行计算,故本选项符合题意;
D、(x﹣y)(﹣x+y)不能用平方差公式进行计算,故本选项不符合题意;
故选:C.
9.解:因为m2+n2=15,(m﹣n)2=1,
所以m2+n2﹣(m﹣n)2=2mn=15﹣1=14,
所以(m+n)2=m2+n2+2mn=15+14=29.
故答案为:29.
10.解:∵a+b=9,ab=14,
∴(a﹣b)2=(a+b)2﹣4ab=92﹣4×14=81﹣56=25,
∴a﹣b=±5.
故答案为:±5.
11.解:∵x﹣y=2,x+y=﹣4,
∴x2﹣y2=(x﹣y)(x+y)=2×(﹣4)=﹣8.
故答案为:﹣8.
12.解:(x+2y﹣z)(x﹣2y+z)=x2﹣(2y﹣z)2=x2﹣4y2+4yz﹣z2.
故答案是:x2﹣4y2+4yz﹣z2.
13.解:原式=(4x2﹣12x+9)﹣(x2﹣y2)﹣y2=4x2﹣12x+9﹣x2+y2﹣y2=3x2﹣12x+9.
故答案为:3x2﹣12x+9.
14.解:∵a+b=﹣6,ab=10,
∴a2﹣ab+b2=(a+b)2﹣3ab=(﹣6)2﹣3×10=36﹣30=6.
故答案为:6.
15.解:∵x2+2(m﹣3)x+9是完全平方式,
∴m﹣3=±3,
解得:m=6或0.
故答案为:6或0.
16.解:(a﹣1)2?(a+1)2=[(a﹣1)(a+1)]2=(a2﹣1)2=a4﹣2a2+1.
故答案为:a4﹣2a2+1.
17.解:原式=(﹣2t+3)(﹣2t﹣3)=(﹣2t)2﹣32=4t2﹣9,故答案为:4t2﹣9.
18.解:设大正方形的边长为a,小正方形的边长为b,
故阴影部分的面积是:AE?BC+AE?BD=AE(BC+BD)
=(AB﹣BE)(BC+BD)=(a﹣b)(a+b)=(a2﹣b2)=×60=30.
故答案为:30.
19.解:∵二次三项式4x2﹣(k﹣5)x+9是完全平方式,
∴k﹣5=±12,
解得:k=17或k=﹣7.
故答案为:17或﹣7.
20.解:∵(2a+3b)2=4a2+12ab+9b2,
(2a﹣3b)2=4a2﹣12ab+9b2,
∴(2a+3b)2=(2a﹣3b)2+24ab,
∴A=24ab,
故答案为:24ab.
21.解:2019×2021﹣20202
=(2000﹣1)×(2000+1)﹣20202=20202﹣1﹣20202=﹣1.
故答案为:﹣1.
22.解:(1)1﹣=(1﹣)×(1+)=,
1﹣=(1﹣)×(1+)=,
故答案为:,,,;
(2)原式=××××××…××××=×
=.
23.解:(1)由图象可知:阴影部分的边长为b﹣a,
故答案为:b﹣a;
(2)由图可知,图1的面积为4ab,图2中白色部分的面积为(a+b)2﹣(b﹣a)2=(a+b)2﹣(a﹣b)2,
∵图1的面积和图2中白色部分的面积相等,
∴(a+b)2﹣(a﹣b)2=4ab,
故答案为:(a+b)2﹣(a﹣b)2=4ab;
(3)根据(1)中的结论,可知(x+y)2﹣(x﹣y)2=4xy,
∵x+y=5,x?y=3,
∴52﹣(x﹣y)2=4×3,
∴(x﹣y)2=13,
故答案为:13;
(4)由图可得,长方形的面积=(a+b)(3a+b),
长方形的面积=3a2+4ab+b2,
∴(a+b)(3a+b)=3a2+4ab+b2.
故答案为:(a+b)(3a+b)=3a2+4ab+b2.
24.解:(1)∵x﹣y=﹣3,xy=﹣2,
∴x2+y2=(x﹣y)2+2xy=9﹣4=5,
∴(x+y)2=x2+2xy+y2=5﹣4=1,
故答案为:5,1;
(2)∵m+n﹣p=﹣10,(m﹣p)n=﹣12,
∴(m﹣p)2+n2=(m﹣p+n)2﹣2(m﹣p)n=100+24=124.
25.解:(1)S阴影部分=S大正方形﹣S小正方形=a2﹣b2,
故答案为:a2﹣b2;
(2)拼成的长方形的长为(a+b),宽为(a﹣b),
所以S阴影部分=S长方形=(a+b)(a﹣b),
故答案为:(a+b)(a﹣b);
(3)由(1)、(2)可得,a2﹣b2=(a+b)(a﹣b);
故答案为:a2﹣b2=(a+b)(a﹣b);
(4)原式=[(a+b)﹣2c][(a+b)+2c]=(a+b)2﹣(2c)2,
=a2+2ab+b2﹣4c2;
(5)∵4x2﹣9y2=(2x+3y)(2x﹣3y)=10,
4x+6y=4,
∴2x+3y=2,
∴2x﹣3y=10÷2=5,
故2x﹣3y的值为5.
26.解:原式=4x2+y2﹣4xy﹣(x2﹣9y2)+4xy﹣4y2
=4x2+y2﹣4xy﹣x2+9y2+4xy﹣4y2=3x2+6y2,
当x=﹣2,y=1时,
原式=3×(﹣2)2+6×12=12+6
=18.
27.解:因为(a+b)2=25,(a﹣b)2=9,
所以(a+b)2﹣(a﹣b)2=4ab=16,
所以a2﹣6ab+b2=(a﹣b)2﹣4ab=9﹣16=﹣7
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
