山东省济南市2012届高三下学期二月 数学(文)
文档属性
| 名称 | 山东省济南市2012届高三下学期二月 数学(文) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-14 00:00:00 | ||
图片预览



文档简介
2011届 高 三 定 时 练 习
数学(文史类)
本练习分第Ⅰ卷和第Ⅱ卷两部分,共8页. 第Ⅰ卷1至2页,第Ⅱ卷3至8页.满分150分,考试时间120分钟.
注意事项:
1. 答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上.
2. 第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上.
参考公式:
如果事件A、B互斥,那么P(AB)=P(A)+P(B); 如果事件A、B独立,那么P(AB)=P(A)·P(B).
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集U={0,1,2,3,4},M ={2,4},N ={0,4},则Cu( MN)=
A .{1,4} B .{3} C.{1,3} D.{0,1,3,4}
2.设复数,则=
A. B. C. D.
3. “”是“不等式”的
A.充分非必要条件 B.充分必要条件
C.必要非充分条件 D.非充分必要条件
4.等差数列中,,则=
A . B . C. D.
5.过点(1,0)且与直线平行的直线方程是
A. B. C. D.
6.函数是
A. 最小正周期为的偶函数 B. 最小正周期为的奇函数
C. 最小正周期为的偶函数 D. 最小正周期为的奇函数
高三数学(文史类)第1页(共8页)
7.已知实数满足,则的最小值是
A.7 B.-3 C. D.3
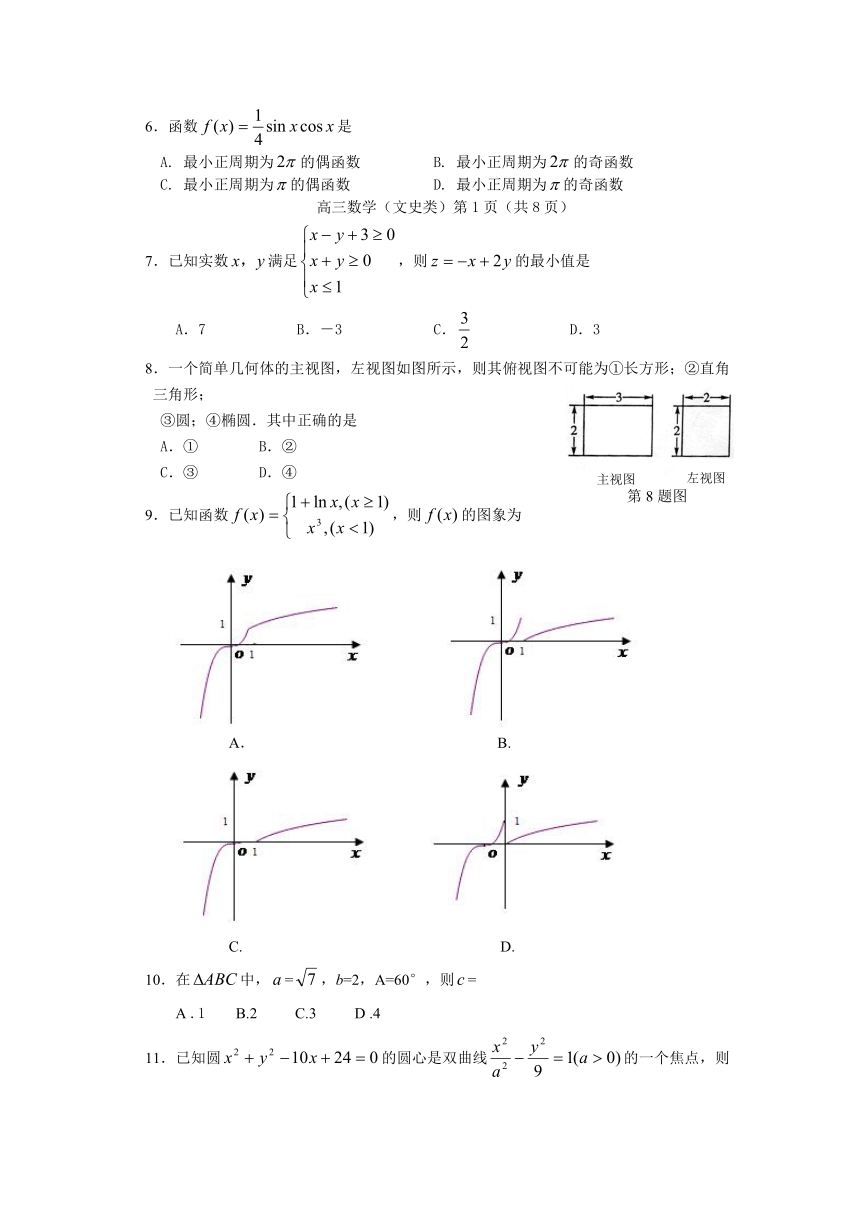
8.一个简单几何体的主视图,左视图如图所示,则其俯视图不可能为①长方形;②直角三角形;
③圆;④椭圆.其中正确的是
A.① B.②
C.③ D.④
9.已知函数,则的图象为
A. B.
C. D.
10.在中,=,b=2,A=60°,则=
A .1 B.2 C.3 D .4
11.已知圆的圆心是双曲线的一个焦点,则此双曲线
的渐近线方程为
A. B. C. D.
12.函数,任取一点,使的概率是
A. B. C. D.
高三数学(文史类)第2页(共8页)
2011届 高 三 定 时 练 习
数学(文史类)
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第Ⅱ卷共6页,所有题目的答案考生须用黑色签字笔、钢笔或蓝圆珠笔在试题卷上答题,考试结束后将答题卡和第Ⅱ卷一并上交.
2.答卷前务必将密封线内的项目填写清楚,密封线内答题无效.
登分栏
题号 二 17 18 19 20 21 22 合计
分数
阅卷人
得分 评卷人
二、填空题:本大题共4个小题,每小题4分,共16分.将答案填在题中横线上.
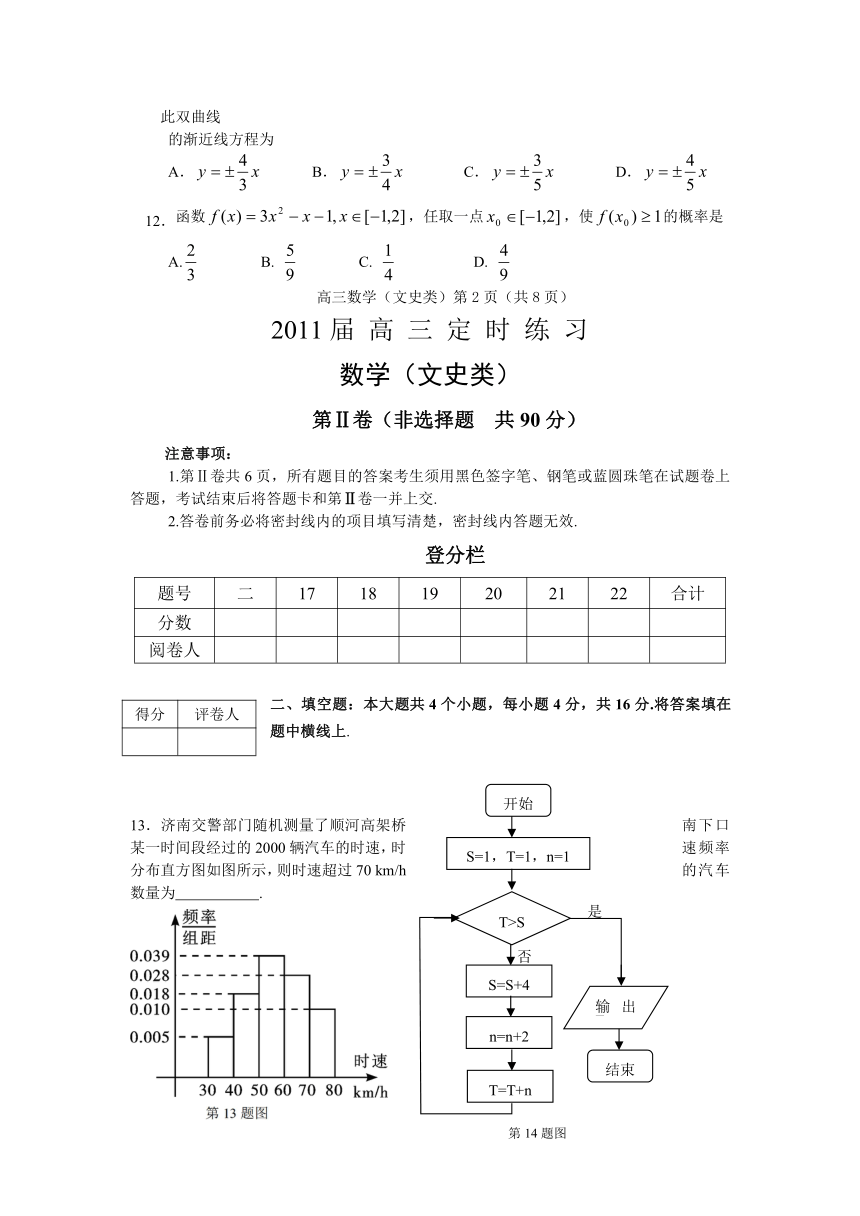
13.济南交警部门随机测量了顺河高架桥南下口某一时间段经过的2000辆汽车的时速,时速频率分布直方图如图所示,则时速超过70 km/h的汽车数量为 .
14.执行如图所示的程序框图,输出的 .
15.用、表示两条不同的直线,、表示两个不同的平面,给出下列命题:
①若∥,∥,则∥; ②若⊥,⊥,则∥;
③若∥,⊥,则⊥; ④若⊥,∥,则⊥.
其中正确的是 .
16.函数零点的个数为 .
高三数学(文史类)第3页(共8页)
三、解答题:本大题共6个小题.共74分.解答应写出文字说明,证明过程或演算步骤.
得分 评卷人
17.(本小题满分12分)
已知函数.
(Ⅰ)求的最小正周期和最大值;
(Ⅱ)求的单调增区间;
(Ⅲ)求在上的最小值.
得分 评卷人
18.(本小题满分12分)
如图,四棱锥中,是的中点,,,面,
且.
(Ⅰ)证明:;
(Ⅱ)证明:面.
高三数学(文史类)第4页(共8页)
得分 评卷人
19.(本小题满分12分)
设平面向量= ( m , 1), = ( 2 , n ),其中 m, n {-2,-1,1,2}.
(I)记“使得⊥成立的( m,n )”为事件A,求事件A发生的概率;
(II)记“使得//(-2)成立的( m,n )”为事件B,求事件B发生的概率.
高三数学(文史类)第5页(共8页)
得分 评卷人
20.(本小题满分12分)
已知数列为等差数列,且,;设数列的前项和为,且.
(Ⅰ)求数列的通项公式;
(Ⅱ)若为数列的前项和,求
高三数学(文史类)第6页(共8页)
得分 评卷人
21.(本小题满分12分)
已知A(,0),B(,0)为平面内两定点,动点P满足|PA|+|PB|=2.
(I)求动点P的轨迹方程;
(II)设直线与(I)中点P的轨迹交于M、N两点.求△BMN的最大面积及此时直线l的方程.
高三数学(文史类)第7页(共8页)
得分 评卷人
22(本小题满分14分)
已知函数,其中.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,求的单调区间;
(Ⅲ)证明:对任意的在区间内均存在零点.
高三数学(文史类)第8页(共8页)
2011届 高 三 定 时 练 习
数学(文史类)参考答案
一、选择题
1.C 2.A 3.A 4.D 5.B 6.D 7.B 8.C 9.A 10.C 11.B 12.D
二、填空题
13. 200 14. 16 15. ②③④ 16. 4
三、解答题
17.解:
(Ⅰ) …………………………………………2分
所以最小正周期为,最大值为2 …………………………………………4分
(Ⅱ) 由 …………………………………………5分
整理,得的单调增区间为: ………………………8分
(Ⅲ)当, ………………………10分
故当x=0时,在上的最小值为-1 ……………………………………………12分
18.证明:
(Ⅰ)由面,,所以. ……………………………3分
又 ,所以. ………………………………………………………………6分
(Ⅱ)取中点,连结,则,且,……………………8分
又 所以是平行四边形, …………9分
,且
所以面. ………………………………12分
19.解:(I)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),
(-1,-2),(-1,-1),(-1,1),(-1,2),(1,-2),(1,-1),(1,1),(1,2),(2,-2),
(2,-1),(2,1),(2,2)共有16种. ……………………………………………………3分
使得⊥成立的( m,n ),满足:2m+n=0, n=-2m
事件A有(-1,2), (1,-2)有2种. ……………………………………………5分
故所求的概率为: ………………………………………………7分
(II)使得//(-2)成立的( m,n )满足:
高三数学(文史类)参考答案第1页(共4页)
m(1-2n)-(m-4)=0即: mn=-2 …………………………………………………9分
事件B有: (-2,1),(-1,2),(1,-2),(2,-1)4种 ……………………………11分
故所求的概率为: ……………………………………………12分
20.解:(Ⅰ)由…………………………1分
………………………………3分
, ……………………………………………………………4分
. ……………………………6分
(Ⅱ)数列为等差数列,公差,可得 …………………………………………8分
从而, …………………………………………………9分
∴
∴
=. …………………………………………………………11分
从而.. …………………………………………………………12分
21.解:(1)∵|PA|+|PB|=2>=|AB|,
∴点P的轨迹是以A,B为焦点,长轴长2a=2的椭圆.…………………………………………2分
∴a=1, …………………………………………4分
设P(x,y),∴点P的轨迹方程为. ………………………………………6分
(2)将代入,
消去x,整理为 …………………………………………7分
设,
高三数学(文史类)参考答案第2页(共4页)
则 …………………………………………8分
= …………………………10分
当且仅当,即时,△BMN的最大面积为
此时直线l的方程是. …………………………………………………………12分
22.解:(Ⅰ)当时,
, …………………………………2分
,
所以曲线在点处的切线方程为. …………………………4分
(Ⅱ),令,解得 …………………………6分
因为,以下分两种情况讨论:
(1)若变化时,的变化情况如下表:
+ +
所以,的单调递增区间是的单调递减区间是.………8分
(2)若,当变化时,的变化情况如下表:
+ +
高三数学(文史类)参考答案第3页(共4页)
所以,的单调递增区间是的单调递减区间是
………………………………………………………………………………………10分
(Ⅲ)由(Ⅱ)可知,当时,在内的单调递减,在内单调递增,
以下分两种情况讨论:
(1)当时,在(0,1)内单调递减,
.
所以对任意在区间(0,1)内均存在零点. …………………………12分
(2)当时,在内单调递减,在内单调递增,
若,
. 所以内存在零点.
若.
, 所以内存在零点. ……………………………………13分
所以,对任意在区间(0,1)内均存在零点.
综上,对任意在区间(0,1)内均存在零点. ………………………………14分
高三数学(文史类)参考答案第4页(共4页)
主视图
左视图
第8题图
开始
S=1,T=1,n=1
T>S
S=S+4
n=n+2
T=T+n
输出T
结束
是
否
第14题图
S
A
B
C
D
M
第18题图
N
数学(文史类)
本练习分第Ⅰ卷和第Ⅱ卷两部分,共8页. 第Ⅰ卷1至2页,第Ⅱ卷3至8页.满分150分,考试时间120分钟.
注意事项:
1. 答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上.
2. 第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上.
参考公式:
如果事件A、B互斥,那么P(AB)=P(A)+P(B); 如果事件A、B独立,那么P(AB)=P(A)·P(B).
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集U={0,1,2,3,4},M ={2,4},N ={0,4},则Cu( MN)=
A .{1,4} B .{3} C.{1,3} D.{0,1,3,4}
2.设复数,则=
A. B. C. D.
3. “”是“不等式”的
A.充分非必要条件 B.充分必要条件
C.必要非充分条件 D.非充分必要条件
4.等差数列中,,则=
A . B . C. D.
5.过点(1,0)且与直线平行的直线方程是
A. B. C. D.
6.函数是
A. 最小正周期为的偶函数 B. 最小正周期为的奇函数
C. 最小正周期为的偶函数 D. 最小正周期为的奇函数
高三数学(文史类)第1页(共8页)
7.已知实数满足,则的最小值是
A.7 B.-3 C. D.3
8.一个简单几何体的主视图,左视图如图所示,则其俯视图不可能为①长方形;②直角三角形;
③圆;④椭圆.其中正确的是
A.① B.②
C.③ D.④
9.已知函数,则的图象为
A. B.
C. D.
10.在中,=,b=2,A=60°,则=
A .1 B.2 C.3 D .4
11.已知圆的圆心是双曲线的一个焦点,则此双曲线
的渐近线方程为
A. B. C. D.
12.函数,任取一点,使的概率是
A. B. C. D.
高三数学(文史类)第2页(共8页)
2011届 高 三 定 时 练 习
数学(文史类)
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第Ⅱ卷共6页,所有题目的答案考生须用黑色签字笔、钢笔或蓝圆珠笔在试题卷上答题,考试结束后将答题卡和第Ⅱ卷一并上交.
2.答卷前务必将密封线内的项目填写清楚,密封线内答题无效.
登分栏
题号 二 17 18 19 20 21 22 合计
分数
阅卷人
得分 评卷人
二、填空题:本大题共4个小题,每小题4分,共16分.将答案填在题中横线上.
13.济南交警部门随机测量了顺河高架桥南下口某一时间段经过的2000辆汽车的时速,时速频率分布直方图如图所示,则时速超过70 km/h的汽车数量为 .
14.执行如图所示的程序框图,输出的 .
15.用、表示两条不同的直线,、表示两个不同的平面,给出下列命题:
①若∥,∥,则∥; ②若⊥,⊥,则∥;
③若∥,⊥,则⊥; ④若⊥,∥,则⊥.
其中正确的是 .
16.函数零点的个数为 .
高三数学(文史类)第3页(共8页)
三、解答题:本大题共6个小题.共74分.解答应写出文字说明,证明过程或演算步骤.
得分 评卷人
17.(本小题满分12分)
已知函数.
(Ⅰ)求的最小正周期和最大值;
(Ⅱ)求的单调增区间;
(Ⅲ)求在上的最小值.
得分 评卷人
18.(本小题满分12分)
如图,四棱锥中,是的中点,,,面,
且.
(Ⅰ)证明:;
(Ⅱ)证明:面.
高三数学(文史类)第4页(共8页)
得分 评卷人
19.(本小题满分12分)
设平面向量= ( m , 1), = ( 2 , n ),其中 m, n {-2,-1,1,2}.
(I)记“使得⊥成立的( m,n )”为事件A,求事件A发生的概率;
(II)记“使得//(-2)成立的( m,n )”为事件B,求事件B发生的概率.
高三数学(文史类)第5页(共8页)
得分 评卷人
20.(本小题满分12分)
已知数列为等差数列,且,;设数列的前项和为,且.
(Ⅰ)求数列的通项公式;
(Ⅱ)若为数列的前项和,求
高三数学(文史类)第6页(共8页)
得分 评卷人
21.(本小题满分12分)
已知A(,0),B(,0)为平面内两定点,动点P满足|PA|+|PB|=2.
(I)求动点P的轨迹方程;
(II)设直线与(I)中点P的轨迹交于M、N两点.求△BMN的最大面积及此时直线l的方程.
高三数学(文史类)第7页(共8页)
得分 评卷人
22(本小题满分14分)
已知函数,其中.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,求的单调区间;
(Ⅲ)证明:对任意的在区间内均存在零点.
高三数学(文史类)第8页(共8页)
2011届 高 三 定 时 练 习
数学(文史类)参考答案
一、选择题
1.C 2.A 3.A 4.D 5.B 6.D 7.B 8.C 9.A 10.C 11.B 12.D
二、填空题
13. 200 14. 16 15. ②③④ 16. 4
三、解答题
17.解:
(Ⅰ) …………………………………………2分
所以最小正周期为,最大值为2 …………………………………………4分
(Ⅱ) 由 …………………………………………5分
整理,得的单调增区间为: ………………………8分
(Ⅲ)当, ………………………10分
故当x=0时,在上的最小值为-1 ……………………………………………12分
18.证明:
(Ⅰ)由面,,所以. ……………………………3分
又 ,所以. ………………………………………………………………6分
(Ⅱ)取中点,连结,则,且,……………………8分
又 所以是平行四边形, …………9分
,且
所以面. ………………………………12分
19.解:(I)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),
(-1,-2),(-1,-1),(-1,1),(-1,2),(1,-2),(1,-1),(1,1),(1,2),(2,-2),
(2,-1),(2,1),(2,2)共有16种. ……………………………………………………3分
使得⊥成立的( m,n ),满足:2m+n=0, n=-2m
事件A有(-1,2), (1,-2)有2种. ……………………………………………5分
故所求的概率为: ………………………………………………7分
(II)使得//(-2)成立的( m,n )满足:
高三数学(文史类)参考答案第1页(共4页)
m(1-2n)-(m-4)=0即: mn=-2 …………………………………………………9分
事件B有: (-2,1),(-1,2),(1,-2),(2,-1)4种 ……………………………11分
故所求的概率为: ……………………………………………12分
20.解:(Ⅰ)由…………………………1分
………………………………3分
, ……………………………………………………………4分
. ……………………………6分
(Ⅱ)数列为等差数列,公差,可得 …………………………………………8分
从而, …………………………………………………9分
∴
∴
=. …………………………………………………………11分
从而.. …………………………………………………………12分
21.解:(1)∵|PA|+|PB|=2>=|AB|,
∴点P的轨迹是以A,B为焦点,长轴长2a=2的椭圆.…………………………………………2分
∴a=1, …………………………………………4分
设P(x,y),∴点P的轨迹方程为. ………………………………………6分
(2)将代入,
消去x,整理为 …………………………………………7分
设,
高三数学(文史类)参考答案第2页(共4页)
则 …………………………………………8分
= …………………………10分
当且仅当,即时,△BMN的最大面积为
此时直线l的方程是. …………………………………………………………12分
22.解:(Ⅰ)当时,
, …………………………………2分
,
所以曲线在点处的切线方程为. …………………………4分
(Ⅱ),令,解得 …………………………6分
因为,以下分两种情况讨论:
(1)若变化时,的变化情况如下表:
+ +
所以,的单调递增区间是的单调递减区间是.………8分
(2)若,当变化时,的变化情况如下表:
+ +
高三数学(文史类)参考答案第3页(共4页)
所以,的单调递增区间是的单调递减区间是
………………………………………………………………………………………10分
(Ⅲ)由(Ⅱ)可知,当时,在内的单调递减,在内单调递增,
以下分两种情况讨论:
(1)当时,在(0,1)内单调递减,
.
所以对任意在区间(0,1)内均存在零点. …………………………12分
(2)当时,在内单调递减,在内单调递增,
若,
. 所以内存在零点.
若.
, 所以内存在零点. ……………………………………13分
所以,对任意在区间(0,1)内均存在零点.
综上,对任意在区间(0,1)内均存在零点. ………………………………14分
高三数学(文史类)参考答案第4页(共4页)
主视图
左视图
第8题图
开始
S=1,T=1,n=1
T>S
S=S+4
n=n+2
T=T+n
输出T
结束
是
否
第14题图
S
A
B
C
D
M
第18题图
N
同课章节目录
