四川省成都南开为明学校2020-2021学年高一3月月考数学试题word含答案
文档属性
| 名称 | 四川省成都南开为明学校2020-2021学年高一3月月考数学试题word含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 130.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 20:59:52 | ||
图片预览

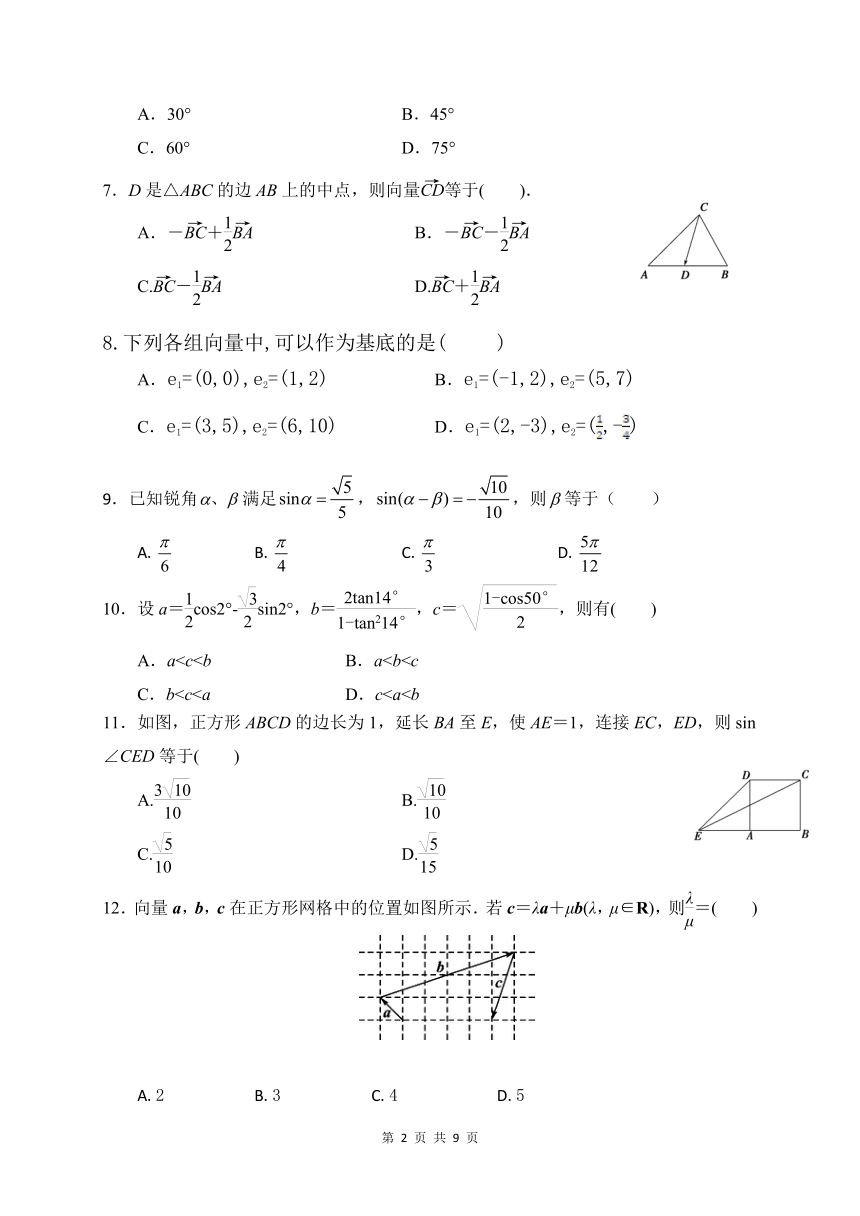


文档简介
成都为明学校20-21学年度下学期3月月考
高一年级 数 学
第Ⅰ卷
一、选择题(本大题共12小题 ,每小题5分 ,共60分.在每小题给出的四个选项中只有
一项是符合题目要求的,请将正确答案的序号涂在答题卡中.)
1.(必修4P78A6改编)给出下列命题:①零向量的长度为零,方向是任意的;②若a,b都是单位向量,则a=b;③向量与相等.则所有正确命题的序号是( )
A.① B.③ C.①③ D.①②
2.(必修4P127T2改编)若cos α=-,α是第三象限的角,则sin等于( )
A.- B. C.- D.
3.cos 45°cos 15°+sin 15°sin 45°的值为( )
A.- B.
C. D.-
4.已知向量=(3,-2),=(-5,-1),则向量的坐标是( )
A. B.
C.(-8,1) D.(8,1)
5.已知tanfalse=3,则tan α的值为( )
A. B.- C. D.-
6.已知向量a=(1-sin θ,1),b=,且a∥b,则锐角θ等于( )
A.30° B.45°
C.60° D.75°
47040802781307.D是△ABC的边AB上的中点,则向量等于( ).
A.-+ B.--
C.- D.+
8.下列各组向量中,可以作为基底的是( )
A.e1=(0,0),e2=(1,2) B.e1=(-1,2),e2=(5,7)
C.e1=(3,5),e2=(6,10) D.e1=(2,-3),e2=(,-)
9.已知锐角false满足false,false,则false等于( )
A.false B.false C.false D.false
10.设a=cos2°-sin2°,b=,c=,则有( )
A.aC.b 518985550292011.如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC,ED,则sin∠CED等于( )
A. B.
C. D.
12.向量a,b,c在正方形网格中的位置如图所示.若c=λa+μb(λ,μ∈R),则=( )
A.2 B.3 C.4 D.5
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分,答案写在答题卡上.)
13. sin15°=__________.
505650546418514.如图,在?ABCD中,=a,=b,用a,b表示向量,,则=________,=________.
15.函数f(x)=sin x-cos的值域为 .
50469803048016.如图,在△ABC中,AD=2BD,AE=3EC,CD与BE交于F,设=a,=b,=xa+yb,则(x,y)为________.
三、解答题(本大题共6小题,17题10分,18-22题每题12分,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.已知a=(-1,2),b=(2,1),p=(9,4)。
(1)计算2a+3b,a-3b; (6分)
(2)若p=ma+nb,求m+n。(4分)
18.已知α∈,sinα=.
(1)求sin的值;
(2)求cos的值.
19.已知两个非零向量a,b不共线,=a+b,=a+2b,=a+3b.
(1)证明:A,B,C三点共线;
(2)试确定实数k,使ka+b与a+kb共线.
20.已知函数f(x)=2sinωxcosωx+ cos2ωx(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的单调递增区间.
21.如图,已知A(4,5),B(1,2),C(12,1),D(11,6),=λ
(1)求λ;
(2)求AC与BD的交点P的坐标.
22.已知函数f(x)=sin(x+π)+cos, x∈R.
(1)求f(x)的最小正周期和最小值;
4392295708025(2)已知cos(β-α)=,cos(β+α)=-,0<α<β≤,求证:[f(β)]2-2=0.
成都为明学校20-21学年度下学期3月考试
高一 数 学
第Ⅰ卷
一、选择题(本大题共12小题 ,每小题5分 ,共60分.在每小题给出的四个选项中只有
一项是符合题目要求的,请将正确答案的序号涂在答题卡中.)
1.解析 根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量与互为相反向量,故③错误.答案 A
2.解析 ∵α是第三象限的角,∴sin α=-=-,∴sin=-×+×=-.答案 C
3.答案 B解析 cos 45°cos 15°+sin 15°sin 45°=cos(45°-15°)=cos 30°=.
4.答案:A [=-=(-5,-1)-(3,-2)=(-8,1),=.]
5.答案:A
6.答案:B [由a∥b,可得(1-sin θ)(1+sin θ)-=0,即cos θ=±,而θ是锐角,故θ=45°.]
7.解析 如图,=+=+=-+.答案 A
8.解析:对于A,e1∥e2,e1,e2是两个共线向量,故不可作为基底;对于B, e1,e2是两个不共线向量,故可作为基底;对于C,e1∥e2,e1,e2是两个共线向量,故不可作为基底;对于D,e1∥e2,e1,e2是两个共线向量,故不可作为基底.故选B.
9.答案:B
10.解:利用三角公式化简得a=cos2°-sin2°=cos(60°+2°)=cos62°=sin28°,
b=tan28°,c==sin25°.
因为sin25° 11.答案:B [由题意知sin∠BEC=,cos∠BEC=,又∠CED=-∠BEC,
所以sin∠CED=sincos∠BEC-cossin∠BEC=×-×=.]
12.解:设i,j分别为水平向右和竖直向上的单位向量,则a=-i+j,b=6i+2j,c=-i-3j,所以-i-3j=λ(-i+j)+μ(6i+2j),即-i-3j=(-λ+6μ)i+(λ+2μ)j,根据平面向量基本定理得 解得 所以=4.故选C.
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分,答案写在答题卡上.)
13.
14.a+b,b-a [由向量加法的平行四边形法则,及向量减法的运算法则可知=a+b,=b-a.]
15.[f(x)=sin x-cos=sin x-cos x+sin x=sin x-cos x=sin,
所以函数f(x)的值域为[-,].
16.解:设=λ,则=+=+λ=+λ=(1-λ)+λ,同理,设=μ,则=+=+μ=μ+(1-μ),根据平面向量基本定理有 解得λ=,所以=+.故填.
三、解答题(本大题共6小题,17题10分,18-22题每题12分,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.[解] (1)2a+3b=2(-1,2)+3(2,1)=(-2,4)+(6,3)=(4,7).
a-3b=(-1,2)-3(2,1)=(-1,2)-(6,3)=(-7,-1).
(2)false [由已知得ma+nb=m(-1,2)+n(2,1)=(-m+2n,2m+n).
又p=(9,4)且p=ma+nb,所以false解得false所以m+n=false.]
18.解:(1)因为α∈,sinα=,所以cosα=-=-.
所以sin=sincosα+cossinα=×+×=-,
(2)由(1)知sin2α=2sinαcosα=2××=-,
cos2α=1-2sin2α=1-2×=,所以cos=coscos2α+sinsin2α
=×+×=-.
19.(1)证明:因为=a+b,=a+2b,=a+3b.所以=-=a+2b-(a+b)=b,
=-=a+3b-(a+b)=2b,所以=2,即与共线.
又因为与有公共点A,所以A,B,C三点共线.
(2)解:因为a,b为非零向量且不共线,所以a+kb≠0.
若ka+b与a+kb共线,则必存在唯一实数λ,
使ka+b=λ(a+kb),整理得(k-λ)a=(λk-1)b.
因此解得或
即存在实数λ=1,使ka+b与a+kb共线,此时k=1;或存在实数λ=-1,使ka+b与a+kb共线,此时k=-1,因此k=±1都满足题意.
20.解:(1)因为f(x)=2sinωxcosωx+cos2ωx=sin2ωx+cos2ωx=sin,
所以f(x)的最小正周期T==.依题意,=π,解得ω=1.
(2)由(1)知f(x)=sin.由2kπ-≤2x+≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z.所以f(x)的单调递增区间为(k∈Ζ).
21.[解] =λ=λ(11-1,6-2)=(10λ,4λ).
易得=(-11,1),
4401820370840∴=+=(10λ-11,4λ+1).
又=(-8,4),而与共线,
∴4×(10λ-11)+8×(4λ+1)=0,
解得λ=.
设点P的坐标为(xP,yP),
∴=(5,2)=(xP-1,yP-2),
∴ 即
故点P的坐标为(6,4).
22.解:(1)f(x)=sinxcos+cosxsin+cosxcos+sinxsin=sinx-cosx=2sin.
所以T=2π,f(x)min=-2.
(2)证明:cos(β-α)=cosαcosβ+sinαsinβ=,①
cos(β+α)=cosαcosβ-sinαsinβ=-,②
①+②得cosαcosβ=0.
因为0<α<β≤,所以cosα∈(0,1),则cosβ=0,β=.
所以f(β)=?[f(β)]2-2=0.
高一年级 数 学
第Ⅰ卷
一、选择题(本大题共12小题 ,每小题5分 ,共60分.在每小题给出的四个选项中只有
一项是符合题目要求的,请将正确答案的序号涂在答题卡中.)
1.(必修4P78A6改编)给出下列命题:①零向量的长度为零,方向是任意的;②若a,b都是单位向量,则a=b;③向量与相等.则所有正确命题的序号是( )
A.① B.③ C.①③ D.①②
2.(必修4P127T2改编)若cos α=-,α是第三象限的角,则sin等于( )
A.- B. C.- D.
3.cos 45°cos 15°+sin 15°sin 45°的值为( )
A.- B.
C. D.-
4.已知向量=(3,-2),=(-5,-1),则向量的坐标是( )
A. B.
C.(-8,1) D.(8,1)
5.已知tanfalse=3,则tan α的值为( )
A. B.- C. D.-
6.已知向量a=(1-sin θ,1),b=,且a∥b,则锐角θ等于( )
A.30° B.45°
C.60° D.75°
47040802781307.D是△ABC的边AB上的中点,则向量等于( ).
A.-+ B.--
C.- D.+
8.下列各组向量中,可以作为基底的是( )
A.e1=(0,0),e2=(1,2) B.e1=(-1,2),e2=(5,7)
C.e1=(3,5),e2=(6,10) D.e1=(2,-3),e2=(,-)
9.已知锐角false满足false,false,则false等于( )
A.false B.false C.false D.false
10.设a=cos2°-sin2°,b=,c=,则有( )
A.a
A. B.
C. D.
12.向量a,b,c在正方形网格中的位置如图所示.若c=λa+μb(λ,μ∈R),则=( )
A.2 B.3 C.4 D.5
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分,答案写在答题卡上.)
13. sin15°=__________.
505650546418514.如图,在?ABCD中,=a,=b,用a,b表示向量,,则=________,=________.
15.函数f(x)=sin x-cos的值域为 .
50469803048016.如图,在△ABC中,AD=2BD,AE=3EC,CD与BE交于F,设=a,=b,=xa+yb,则(x,y)为________.
三、解答题(本大题共6小题,17题10分,18-22题每题12分,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.已知a=(-1,2),b=(2,1),p=(9,4)。
(1)计算2a+3b,a-3b; (6分)
(2)若p=ma+nb,求m+n。(4分)
18.已知α∈,sinα=.
(1)求sin的值;
(2)求cos的值.
19.已知两个非零向量a,b不共线,=a+b,=a+2b,=a+3b.
(1)证明:A,B,C三点共线;
(2)试确定实数k,使ka+b与a+kb共线.
20.已知函数f(x)=2sinωxcosωx+ cos2ωx(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的单调递增区间.
21.如图,已知A(4,5),B(1,2),C(12,1),D(11,6),=λ
(1)求λ;
(2)求AC与BD的交点P的坐标.
22.已知函数f(x)=sin(x+π)+cos, x∈R.
(1)求f(x)的最小正周期和最小值;
4392295708025(2)已知cos(β-α)=,cos(β+α)=-,0<α<β≤,求证:[f(β)]2-2=0.
成都为明学校20-21学年度下学期3月考试
高一 数 学
第Ⅰ卷
一、选择题(本大题共12小题 ,每小题5分 ,共60分.在每小题给出的四个选项中只有
一项是符合题目要求的,请将正确答案的序号涂在答题卡中.)
1.解析 根据零向量的定义可知①正确;根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;向量与互为相反向量,故③错误.答案 A
2.解析 ∵α是第三象限的角,∴sin α=-=-,∴sin=-×+×=-.答案 C
3.答案 B解析 cos 45°cos 15°+sin 15°sin 45°=cos(45°-15°)=cos 30°=.
4.答案:A [=-=(-5,-1)-(3,-2)=(-8,1),=.]
5.答案:A
6.答案:B [由a∥b,可得(1-sin θ)(1+sin θ)-=0,即cos θ=±,而θ是锐角,故θ=45°.]
7.解析 如图,=+=+=-+.答案 A
8.解析:对于A,e1∥e2,e1,e2是两个共线向量,故不可作为基底;对于B, e1,e2是两个不共线向量,故可作为基底;对于C,e1∥e2,e1,e2是两个共线向量,故不可作为基底;对于D,e1∥e2,e1,e2是两个共线向量,故不可作为基底.故选B.
9.答案:B
10.解:利用三角公式化简得a=cos2°-sin2°=cos(60°+2°)=cos62°=sin28°,
b=tan28°,c==sin25°.
因为sin25°
所以sin∠CED=sincos∠BEC-cossin∠BEC=×-×=.]
12.解:设i,j分别为水平向右和竖直向上的单位向量,则a=-i+j,b=6i+2j,c=-i-3j,所以-i-3j=λ(-i+j)+μ(6i+2j),即-i-3j=(-λ+6μ)i+(λ+2μ)j,根据平面向量基本定理得 解得 所以=4.故选C.
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分,答案写在答题卡上.)
13.
14.a+b,b-a [由向量加法的平行四边形法则,及向量减法的运算法则可知=a+b,=b-a.]
15.[f(x)=sin x-cos=sin x-cos x+sin x=sin x-cos x=sin,
所以函数f(x)的值域为[-,].
16.解:设=λ,则=+=+λ=+λ=(1-λ)+λ,同理,设=μ,则=+=+μ=μ+(1-μ),根据平面向量基本定理有 解得λ=,所以=+.故填.
三、解答题(本大题共6小题,17题10分,18-22题每题12分,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.[解] (1)2a+3b=2(-1,2)+3(2,1)=(-2,4)+(6,3)=(4,7).
a-3b=(-1,2)-3(2,1)=(-1,2)-(6,3)=(-7,-1).
(2)false [由已知得ma+nb=m(-1,2)+n(2,1)=(-m+2n,2m+n).
又p=(9,4)且p=ma+nb,所以false解得false所以m+n=false.]
18.解:(1)因为α∈,sinα=,所以cosα=-=-.
所以sin=sincosα+cossinα=×+×=-,
(2)由(1)知sin2α=2sinαcosα=2××=-,
cos2α=1-2sin2α=1-2×=,所以cos=coscos2α+sinsin2α
=×+×=-.
19.(1)证明:因为=a+b,=a+2b,=a+3b.所以=-=a+2b-(a+b)=b,
=-=a+3b-(a+b)=2b,所以=2,即与共线.
又因为与有公共点A,所以A,B,C三点共线.
(2)解:因为a,b为非零向量且不共线,所以a+kb≠0.
若ka+b与a+kb共线,则必存在唯一实数λ,
使ka+b=λ(a+kb),整理得(k-λ)a=(λk-1)b.
因此解得或
即存在实数λ=1,使ka+b与a+kb共线,此时k=1;或存在实数λ=-1,使ka+b与a+kb共线,此时k=-1,因此k=±1都满足题意.
20.解:(1)因为f(x)=2sinωxcosωx+cos2ωx=sin2ωx+cos2ωx=sin,
所以f(x)的最小正周期T==.依题意,=π,解得ω=1.
(2)由(1)知f(x)=sin.由2kπ-≤2x+≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z.所以f(x)的单调递增区间为(k∈Ζ).
21.[解] =λ=λ(11-1,6-2)=(10λ,4λ).
易得=(-11,1),
4401820370840∴=+=(10λ-11,4λ+1).
又=(-8,4),而与共线,
∴4×(10λ-11)+8×(4λ+1)=0,
解得λ=.
设点P的坐标为(xP,yP),
∴=(5,2)=(xP-1,yP-2),
∴ 即
故点P的坐标为(6,4).
22.解:(1)f(x)=sinxcos+cosxsin+cosxcos+sinxsin=sinx-cosx=2sin.
所以T=2π,f(x)min=-2.
(2)证明:cos(β-α)=cosαcosβ+sinαsinβ=,①
cos(β+α)=cosαcosβ-sinαsinβ=-,②
①+②得cosαcosβ=0.
因为0<α<β≤,所以cosα∈(0,1),则cosβ=0,β=.
所以f(β)=?[f(β)]2-2=0.
同课章节目录
