六年级上册数学教案-2.2 圆的周长 西师大版
文档属性
| 名称 | 六年级上册数学教案-2.2 圆的周长 西师大版 |

|
|
| 格式 | doc | ||
| 文件大小 | 42.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览



文档简介
圆的周长教案
教材分析与学情:
本节课是在学生通过前面的学习已获得了圆周率和圆的周长计算公式的初步知识。在教法上,复习上节课的内容,导引到新课内容,在此过程中发挥学生的自主性,积极投入学习中;又在各个环节中设置由浅入深,由易到难的问题,引导学生独立思考、掌握方法、强化练习。在学情上, 课堂上关注两三位学困生,真正做到面上全体学生。学生是学习的主体,是知识建构的主动者。高年级学生能运用已有知识通过里顺知识和应用知识的能力,加强并运用新知解决实际问题。他们在小组合作的学习环境下,利用自主探索的学习方式,学习的积极性较高,他们善于探索,敢于质疑,敢于创新,同时多媒体辅助教学软件的运用,更易给他们直观的体验,反馈也更及时有效。
教学目标:
1、使学生进一步掌握圆的周长公式,会根据圆的直径(或半径)求出圆的周长和根据圆的周长求出圆的直径和半径,并能运用公式解决简单的实际问题。
2、在学习中进一步积累认识图形的学习经验,增强空间观念,发展数学思考。
3、使学生进一步体验图形与生活的联系,感受平面图形的学习价值,提高数学学习的兴趣和学好数学的自信心。
教学重难点:运用圆的周长计算公式,解决简单的实际问题。
教学课时:1课时
教学课型:新授课
教学准备: 多媒体课件、圆形物品及细线。
教学过程:
一、复习引入:
师:上节课我学习了哪些知识?
生:圆周率、圆的周长计算公式:C=πd或C=2πr。
课件展示:圆的周长和直径的商是一个固定的数,圆的周长除以直径的商是 一个固定的数,我们把它叫做圆周率,用字母π表示。C=πd或C=2πr
计算时,通常取π的近似值, π≈3.14
导入新课:
师:根据圆的周长公式,如果我们知道了圆的直径或半径,可以求出圆的周长。如果已知圆的周长,也可以求出圆的直径和半径。下面我们继续学习利用圆的周长公式来进行相关的计算。
(设计意图:通过复习上节课的圆的周长计算公式,使学生懂得已知直径或半径,可以求出圆的周长;已知圆的周长,也可以求圆的直径或半径。)
二、教学新课:
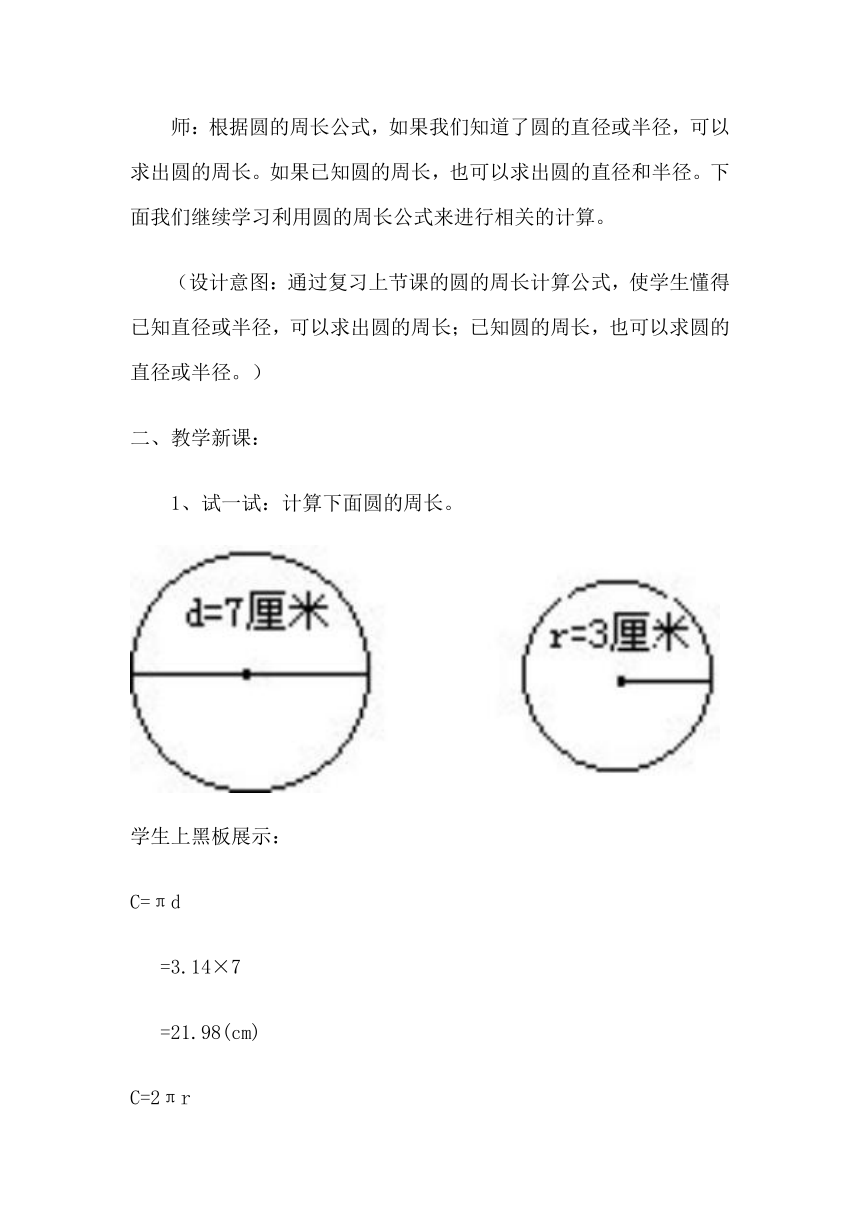
1、试一试:计算下面圆的周长。
学生上黑板展示:
C=πd
=3.14×7
=21.98(cm)
C=2πr
=2×3.14×3
=18.84(cm)
强调和纠正规范书写
2、教学例2,用圆周长公式解决实际问题
(1)出示例2图:(学生读题)
例② 自行车车轮的外直径约是0.71m。车轮转一周,自行车约前进多少米?(保留两位小数)
师:该题是已知什么量,求什么量?
(在小组中说说自己的方法,然后汇报)
(2)学生汇报方法。
解:C= πd
=3.14×0.71
=2.2294
≈2.23(m)
答:自行车约前进2.23米。
3、如果已知一个圆的周长,我们是否可以求出它的直径和半径呢?学习例题3
师:如果让我们直接测量这个水池的直径方便吗?为什么?
生:不方便。太大了。
师:对了,但我们可以用软尺子绕水池一周,测量出它的周长。现在告诉我们水池的周长是31.4米,你能想办法求出它的直径和半径是多少米吗?
师:你觉得这题与例2相比较,有什么不同?
生:这里是已知圆的周长,求直径和半径。例2是已知圆的直径求周长,
师:好了,你是怎样算的?在小组里交流一下。
(在小组中说说自己的方法,然后汇报)
学生汇报方法。
生1:用31.4÷3.14;
生2:可以根据C= πd列方程解。
师:你是怎样想到这个方法的?
生:因为圆周率×直径=圆的周长(C=πd ,d= C÷π)。
师:很好。怎样列式?
生:用31.4÷3.14=10(米);
师:列方程解应该怎样解啊?
(学生展示)
解:根据C=πd得:d= C÷π
=31.4÷3.14
=10(米)
r=d÷2
=10÷2
=5(米)
答:水池的直径是10米,半径是5米。
师:当在计算有关圆的周长知识时,如数据较大的计算,可以用计算器计算。好了,以后像这样的题,我们根据圆的周长求直径可以列方程解,也可以直接用除法计算。
(设计意图:运用对比的手段,让小孩找出不同点,从而采用相应的解决方法,做到熟练运用圆的周长计算公式的能力。又通过交流找到解决问题不同方法的依据。)
三、课堂活动:
1、议一议:哪个图形的周长长一些?是怎样比的?
学生讨论交流,指名汇报说出理由
2、测量一个圆形物品上圆的周长,再算出它的直径和半径。
学生活动:分组发放准备好的圆形物品(指南针)和细线,动手测量其周长,并计算直径和半径
小组汇报:
(设计意图:复习上节课学过的测量圆形物品周长的方法,巩固利用周长求圆直径和半径的计算)
3、练一练:
完成课后2—7题:
四、课内总结:
师:今天我们学习了什么内容?你有哪些收获?觉得自己的课堂表现如何?
板书设计:
圆的周长计算实际运用
C=πd或C=2πr。
解:C= πd
=3.14×0.71
=2.2294
≈2.23(m)
答:自行车约前进2.23米。
教材分析与学情:
本节课是在学生通过前面的学习已获得了圆周率和圆的周长计算公式的初步知识。在教法上,复习上节课的内容,导引到新课内容,在此过程中发挥学生的自主性,积极投入学习中;又在各个环节中设置由浅入深,由易到难的问题,引导学生独立思考、掌握方法、强化练习。在学情上, 课堂上关注两三位学困生,真正做到面上全体学生。学生是学习的主体,是知识建构的主动者。高年级学生能运用已有知识通过里顺知识和应用知识的能力,加强并运用新知解决实际问题。他们在小组合作的学习环境下,利用自主探索的学习方式,学习的积极性较高,他们善于探索,敢于质疑,敢于创新,同时多媒体辅助教学软件的运用,更易给他们直观的体验,反馈也更及时有效。
教学目标:
1、使学生进一步掌握圆的周长公式,会根据圆的直径(或半径)求出圆的周长和根据圆的周长求出圆的直径和半径,并能运用公式解决简单的实际问题。
2、在学习中进一步积累认识图形的学习经验,增强空间观念,发展数学思考。
3、使学生进一步体验图形与生活的联系,感受平面图形的学习价值,提高数学学习的兴趣和学好数学的自信心。
教学重难点:运用圆的周长计算公式,解决简单的实际问题。
教学课时:1课时
教学课型:新授课
教学准备: 多媒体课件、圆形物品及细线。
教学过程:
一、复习引入:
师:上节课我学习了哪些知识?
生:圆周率、圆的周长计算公式:C=πd或C=2πr。
课件展示:圆的周长和直径的商是一个固定的数,圆的周长除以直径的商是 一个固定的数,我们把它叫做圆周率,用字母π表示。C=πd或C=2πr
计算时,通常取π的近似值, π≈3.14
导入新课:
师:根据圆的周长公式,如果我们知道了圆的直径或半径,可以求出圆的周长。如果已知圆的周长,也可以求出圆的直径和半径。下面我们继续学习利用圆的周长公式来进行相关的计算。
(设计意图:通过复习上节课的圆的周长计算公式,使学生懂得已知直径或半径,可以求出圆的周长;已知圆的周长,也可以求圆的直径或半径。)
二、教学新课:
1、试一试:计算下面圆的周长。
学生上黑板展示:
C=πd
=3.14×7
=21.98(cm)
C=2πr
=2×3.14×3
=18.84(cm)
强调和纠正规范书写
2、教学例2,用圆周长公式解决实际问题
(1)出示例2图:(学生读题)
例② 自行车车轮的外直径约是0.71m。车轮转一周,自行车约前进多少米?(保留两位小数)
师:该题是已知什么量,求什么量?
(在小组中说说自己的方法,然后汇报)
(2)学生汇报方法。
解:C= πd
=3.14×0.71
=2.2294
≈2.23(m)
答:自行车约前进2.23米。
3、如果已知一个圆的周长,我们是否可以求出它的直径和半径呢?学习例题3
师:如果让我们直接测量这个水池的直径方便吗?为什么?
生:不方便。太大了。
师:对了,但我们可以用软尺子绕水池一周,测量出它的周长。现在告诉我们水池的周长是31.4米,你能想办法求出它的直径和半径是多少米吗?
师:你觉得这题与例2相比较,有什么不同?
生:这里是已知圆的周长,求直径和半径。例2是已知圆的直径求周长,
师:好了,你是怎样算的?在小组里交流一下。
(在小组中说说自己的方法,然后汇报)
学生汇报方法。
生1:用31.4÷3.14;
生2:可以根据C= πd列方程解。
师:你是怎样想到这个方法的?
生:因为圆周率×直径=圆的周长(C=πd ,d= C÷π)。
师:很好。怎样列式?
生:用31.4÷3.14=10(米);
师:列方程解应该怎样解啊?
(学生展示)
解:根据C=πd得:d= C÷π
=31.4÷3.14
=10(米)
r=d÷2
=10÷2
=5(米)
答:水池的直径是10米,半径是5米。
师:当在计算有关圆的周长知识时,如数据较大的计算,可以用计算器计算。好了,以后像这样的题,我们根据圆的周长求直径可以列方程解,也可以直接用除法计算。
(设计意图:运用对比的手段,让小孩找出不同点,从而采用相应的解决方法,做到熟练运用圆的周长计算公式的能力。又通过交流找到解决问题不同方法的依据。)
三、课堂活动:
1、议一议:哪个图形的周长长一些?是怎样比的?
学生讨论交流,指名汇报说出理由
2、测量一个圆形物品上圆的周长,再算出它的直径和半径。
学生活动:分组发放准备好的圆形物品(指南针)和细线,动手测量其周长,并计算直径和半径
小组汇报:
(设计意图:复习上节课学过的测量圆形物品周长的方法,巩固利用周长求圆直径和半径的计算)
3、练一练:
完成课后2—7题:
四、课内总结:
师:今天我们学习了什么内容?你有哪些收获?觉得自己的课堂表现如何?
板书设计:
圆的周长计算实际运用
C=πd或C=2πr。
解:C= πd
=3.14×0.71
=2.2294
≈2.23(m)
答:自行车约前进2.23米。
