8.3.1棱柱、棱锥、棱台的表面积和体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(19张PPT)
文档属性
| 名称 | 8.3.1棱柱、棱锥、棱台的表面积和体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览


文档简介
8.3.1棱柱、棱锥、棱台的表面积和体积
温故知新
请同学回顾下面公式
矩形面积公式:
三角形面积公式:
梯形面积公式:
长方体体积:
正方体体积:
有记不住的同学请你抄下来!!
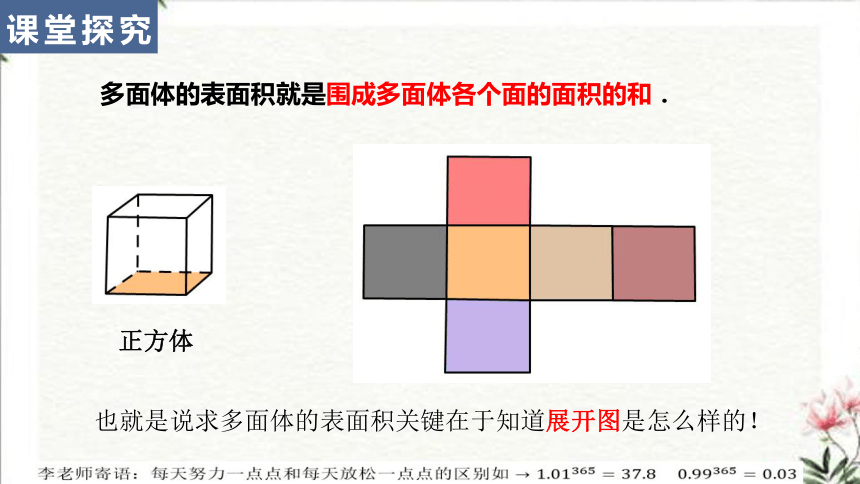
多面体的表面积就是围成多面体各个面的面积的和.
正方体
也就是说求多面体的表面积关键在于知道展开图是怎么样的!
课堂探究
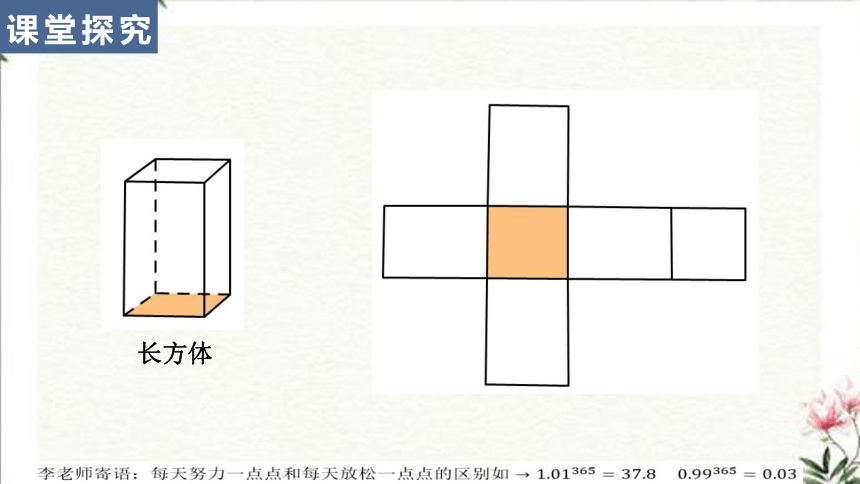
长方体
课堂探究
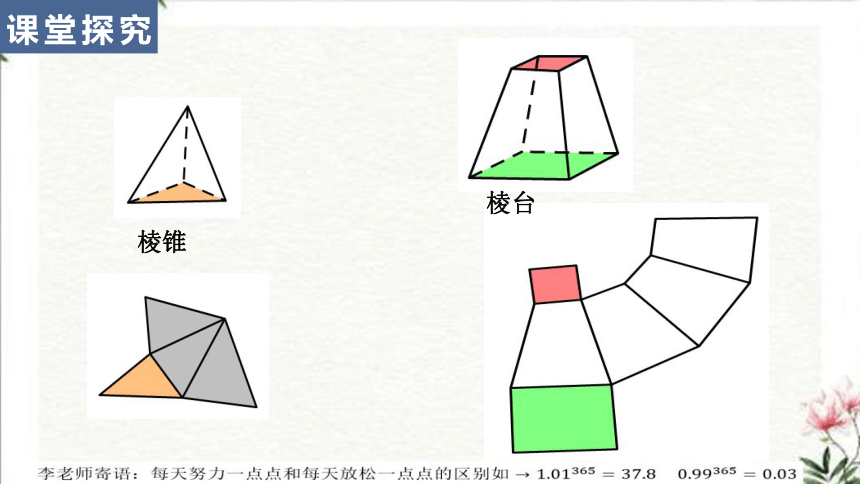
棱锥
棱台
课堂探究
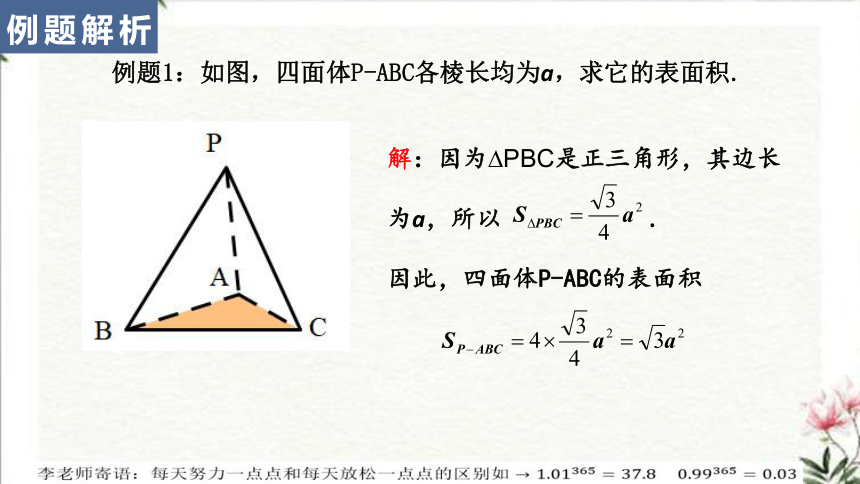
例题1:如图,四面体P-ABC各棱长均为a,求它的表面积.
解:因为?PBC是正三角形,其边长
为a,所以 .
因此,四面体P-ABC的表面积
例题解析
?
?
?
?
?
?
?
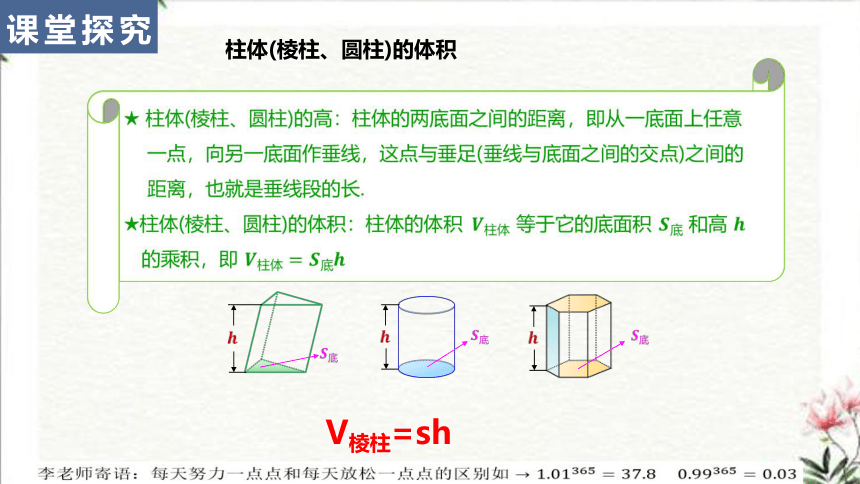
柱体(棱柱、圆柱)的体积
V棱柱=sh
课堂探究
?
?
?
锥体(棱锥、圆锥)的体积
推导过程感兴趣可以查阅祖暅原理
课堂探究
棱柱与棱锥体积之间的关系
一个三棱柱可以分解成三个体积相等的三棱锥,如图所示:
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
课堂探究
棱台的体积又应该是怎样的呢?
课堂探究
课堂探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}几何体
柱体
锥体
台体
直
观
图
体
积
重要
!
课堂探究
例2:如右图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米?
A'
B'
C'
D'
A
B
C
D
P
解:
如右下图,由题意知
V长方体ADCD-A'B'C'D'=1×1×0.5=0.5(m3),
V棱锥P-ABCD=
×1×1×0.5=
(m3)
所以这个漏斗的容积
V=0.5+ =
(m3)
例题解析
1、三棱锥P-ABC中,PA⊥底面ABC,PA=3.底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于_______
解:依题意有,三棱锥P-ABC的体积V=??????????????????????????????????=????????×????????×????????×????=????
?
练习巩固
2、如图,在棱长为4的正方体ABCD-????????????????????????????????中,P 是????????????????上一点,且P????????=????????????????????????,则多面体P-BC????????????????的体积为( )
A ????????????????? B ????????????? C 4 D 2
?
解:所求多面体为四棱锥,且高为PB1=1,底面面积为4×????=16.所以其体积为????????×????????×????=????????????
?
练习巩固
3、某几何体的三视图如图所示,则该几何体的表面积为( )
A.54 B.60 C.66 D.72
B
练习巩固
4、已知一个正四棱锥P-ABCD的侧棱长为5,底面的边长为6,高为7.求它的表面积和体积.
练习巩固
表面积:84 体积:84
你学到了什么?
你认为易错点是哪些?
课堂小结
1、棱柱、棱锥、棱台的表面积
S棱柱表=S棱柱侧+2S底
S棱锥表=S棱锥侧+S底
S棱台表=S棱台侧+S上底+S下底
2、棱柱、棱锥、棱台的体积
V棱柱=Sh(S为底面面积,h为高)
V棱锥= Sh(S为底面面积,h为高)
(S',S分别为棱台的上下底面面积,h为棱台的高
作业1:报纸34期2版8.3.1
作业2:书P116
(请课代表中午2:00检查)
附加:新优化P23--P24
作业布置
温故知新
请同学回顾下面公式
矩形面积公式:
三角形面积公式:
梯形面积公式:
长方体体积:
正方体体积:
有记不住的同学请你抄下来!!
多面体的表面积就是围成多面体各个面的面积的和.
正方体
也就是说求多面体的表面积关键在于知道展开图是怎么样的!
课堂探究
长方体
课堂探究
棱锥
棱台
课堂探究
例题1:如图,四面体P-ABC各棱长均为a,求它的表面积.
解:因为?PBC是正三角形,其边长
为a,所以 .
因此,四面体P-ABC的表面积
例题解析
?
?
?
?
?
?
?
柱体(棱柱、圆柱)的体积
V棱柱=sh
课堂探究
?
?
?
锥体(棱锥、圆锥)的体积
推导过程感兴趣可以查阅祖暅原理
课堂探究
棱柱与棱锥体积之间的关系
一个三棱柱可以分解成三个体积相等的三棱锥,如图所示:
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
课堂探究
棱台的体积又应该是怎样的呢?
课堂探究
课堂探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}几何体
柱体
锥体
台体
直
观
图
体
积
重要
!
课堂探究
例2:如右图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米?
A'
B'
C'
D'
A
B
C
D
P
解:
如右下图,由题意知
V长方体ADCD-A'B'C'D'=1×1×0.5=0.5(m3),
V棱锥P-ABCD=
×1×1×0.5=
(m3)
所以这个漏斗的容积
V=0.5+ =
(m3)
例题解析
1、三棱锥P-ABC中,PA⊥底面ABC,PA=3.底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于_______
解:依题意有,三棱锥P-ABC的体积V=??????????????????????????????????=????????×????????×????????×????=????
?
练习巩固
2、如图,在棱长为4的正方体ABCD-????????????????????????????????中,P 是????????????????上一点,且P????????=????????????????????????,则多面体P-BC????????????????的体积为( )
A ????????????????? B ????????????? C 4 D 2
?
解:所求多面体为四棱锥,且高为PB1=1,底面面积为4×????=16.所以其体积为????????×????????×????=????????????
?
练习巩固
3、某几何体的三视图如图所示,则该几何体的表面积为( )
A.54 B.60 C.66 D.72
B
练习巩固
4、已知一个正四棱锥P-ABCD的侧棱长为5,底面的边长为6,高为7.求它的表面积和体积.
练习巩固
表面积:84 体积:84
你学到了什么?
你认为易错点是哪些?
课堂小结
1、棱柱、棱锥、棱台的表面积
S棱柱表=S棱柱侧+2S底
S棱锥表=S棱锥侧+S底
S棱台表=S棱台侧+S上底+S下底
2、棱柱、棱锥、棱台的体积
V棱柱=Sh(S为底面面积,h为高)
V棱锥= Sh(S为底面面积,h为高)
(S',S分别为棱台的上下底面面积,h为棱台的高
作业1:报纸34期2版8.3.1
作业2:书P116
(请课代表中午2:00检查)
附加:新优化P23--P24
作业布置
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
