2020-2021学年人教版八年级下册数学 18.2.2菱形 同步测试(Word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 18.2.2菱形 同步测试(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 191.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览


文档简介
18.2.2菱形 同步测试
一.选择题
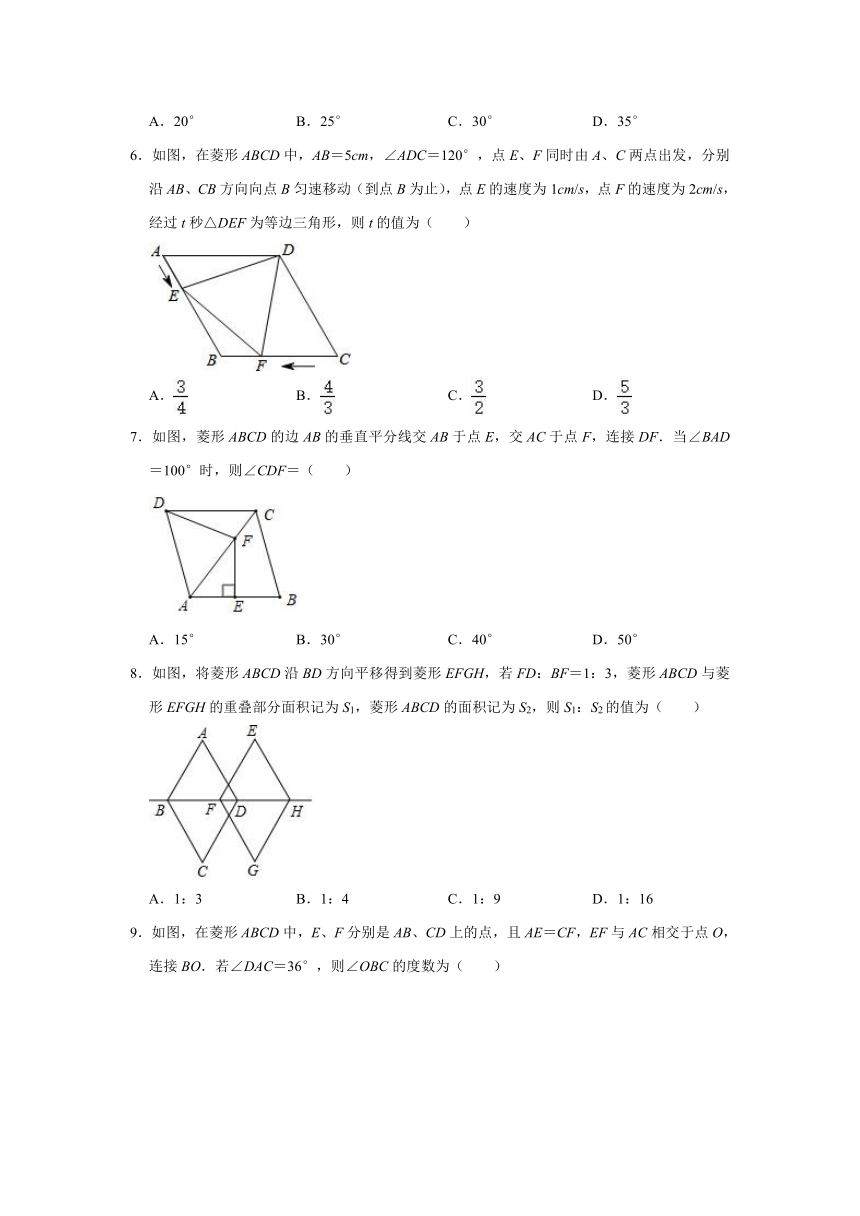
1.如图,菱形ABCD中,∠A=50°,则∠ADB的度数为( )
A.65° B.55° C.45° D.25°
2.下列说法正确的是( )
A.对角线相等的四边形是菱形
B.四条边相等的四边形是菱形
C.一组邻边相等的四边形是菱形
D.对角线互相垂直的四边形是菱形
3.如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( )
A. B. C. D.
4.下列关系中,是菱形的性质但不是平行四边形的性质的是( )
A.对角线垂直 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
5.如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是( )
A.20° B.25° C.30° D.35°
6.如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A. B. C. D.
7.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当∠BAD=100°时,则∠CDF=( )
A.15° B.30° C.40° D.50°
8.如图,将菱形ABCD沿BD方向平移得到菱形EFGH,若FD:BF=1:3,菱形ABCD与菱形EFGH的重叠部分面积记为S1,菱形ABCD的面积记为S2,则S1:S2的值为( )
A.1:3 B.1:4 C.1:9 D.1:16
9.如图,在菱形ABCD中,E、F分别是AB、CD上的点,且AE=CF,EF与AC相交于点O,连接BO.若∠DAC=36°,则∠OBC的度数为( )
A.36° B.54° C.64° D.72°
10.如图,在菱形ABCD中,对角线AC,BD交于点E,延长BC到点F,使CF=BC,连接AF,DF,AF分别交CD,BD于点G,O,则下列结论错误的是( )
A.四边形ACFD是平行四边形
B.BD2+FD2=BF2
C.OE=BD
D.面积关系:S△GEO=S△ADO
二.填空题
11.如图,四边形ABCD的对角线AC与BD交于点O,AC⊥BD,且AC平分BD,若添加一个条件 ,则四边形ABCD为菱形.
12.若一个菱形的周长为200cm,一条对角线长为60cm,则它的面积为 .
13.菱形有一个内角为120°,较长的对角线长为6,则它的面积为 .
14.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF= .
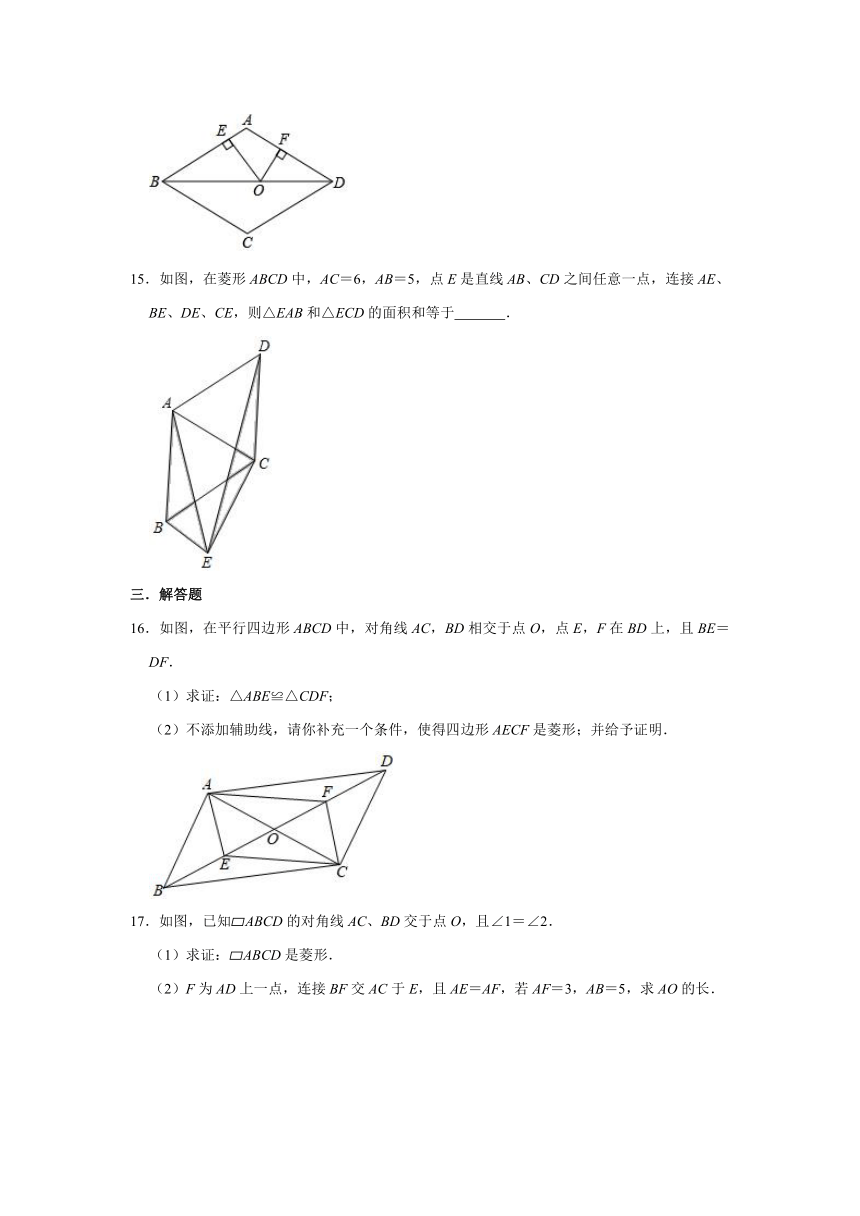
15.如图,在菱形ABCD中,AC=6,AB=5,点E是直线AB、CD之间任意一点,连接AE、BE、DE、CE,则△EAB和△ECD的面积和等于 .
三.解答题
16.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在BD上,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)不添加辅助线,请你补充一个条件,使得四边形AECF是菱形;并给予证明.
17.如图,已知?ABCD的对角线AC、BD交于点O,且∠1=∠2.
(1)求证:?ABCD是菱形.
(2)F为AD上一点,连接BF交AC于E,且AE=AF,若AF=3,AB=5,求AO的长.
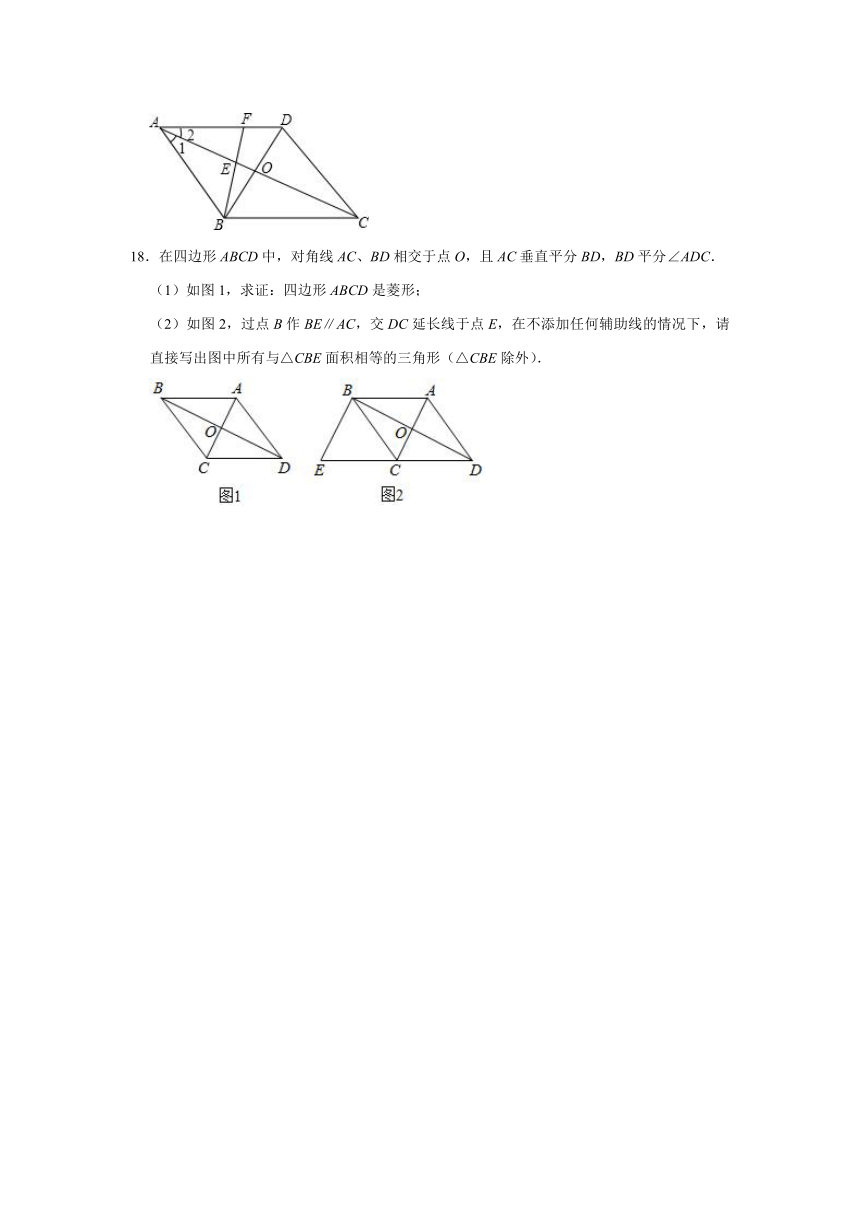
18.在四边形ABCD中,对角线AC、BD相交于点O,且AC垂直平分BD,BD平分∠ADC.
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,过点B作BE∥AC,交DC延长线于点E,在不添加任何辅助线的情况下,请直接写出图中所有与△CBE面积相等的三角形(△CBE除外).
参考答案
一.选择题
1.解:∵四边形ABCD是菱形,
∴AB∥CD,∠ADB=∠CDB,
∴∠A+∠ADC=180°,
∵∠A=50°,
∴∠ADC=130°,
∴∠ADB=×130°=65°,
故选:A.
2.解:A.对角线相等的平行四边形是矩形,故不符合题意;
B.四条边相等的四边形是菱形,故符合题意;
C.一组邻边相等的平行四边形是菱形,故不符合题意;
D.对角线互相垂直的平行四边形是菱形,故不符合题意;
故选:B.
3.解:∵四边形ABCD是菱形,
∴CO=AC=3,BO=BD=4,AO⊥BO,
∴BC===5,
∵S菱形ABCD=AC?BD=BC×AE,
∴AE==.
在Rt△ABE中,BE===,
∴CE=BC﹣BE=5﹣=,
∴的值为,
故选:C.
4.解:A、菱形的对角线互相垂直平分、平行四边形的对角线互相平分,符合题意;
B、菱形、平行四边形的对边平行且相等,不符合题意;
C、菱形、平行四边形的对角线互相平分,不符合题意;
D、菱形、平行四边形的两组对角分别相等,不符合题意;
故选:A.
5.解:如图:
∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠HDO=∠DHO,
∵DH⊥CD,
∴∠GDO+∠ODC=90°,
∵BD⊥AC,
∴∠ODC+∠DCO=90°,
∴∠HDO=∠DCO,
∴∠DHO=∠DCA,
∵四边形ABCD是菱形,
∴DA=DC,
∴∠CAD=∠DCA=25°,
∴∠DHO=25°,
故选:B.
6.解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADB=∠ADC=60°,
∴△ABD是等边三角形,
∴AD=BD,
又∵△DEF是等边三角形,
∴∠EDF=∠DEF=60°,
又∵∠ADB=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,,
∴△ADE≌△BDF(ASA),
∴AE=BF,
∵AE=t,CF=2t,
∴BF=BC﹣CF=5﹣2t,
∴t=5﹣2t
∴t=,
故选:D.
7.解:如图,连接BF,
∵四边形ABCD是菱形,
∴CD=BC,∠DCF=∠BCF,
在△BCF和△DCF中,
∵,
∴△BCF≌△DCF(SAS)
∴∠CBF=∠CDF
∵FE垂直平分AB,∠BAF=×100°=50°
∴∠ABF=∠BAF=50°
∵∠ABC=180°﹣100°=80°,∠CBF=80°﹣50°=30°
∴∠CDF=30°.
故选:B.
8.解:如图设AD交EF于M,CD交FG于N.
由题意,重叠部分四边形MDNF是菱形,
菱形MFND∽菱形ABCD,
∴=()2,
∵DF:BF=1:3,
∴DF:BD=1:4,
∴=()2=,
故选:D.
9.解:∵四边形ABCD是菱形,
∴AB=BC=AD=CD,AB∥CD,AD∥BC,
∴∠EAO=∠FCO,∠DAC=∠ACB=36°,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AO=CO,
又∵AB=BC,
∴BO⊥AC,
∴∠OBC=90°﹣∠ACB=54°,
故选:B.
10.解:∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,AE=EC,BE=DE,AC⊥BD,
∵CF=BC,
∴CF=AD,
∴四边形ACFD是平行四边形,故选项A不合题意;
∴AC∥DF,DG=GC,
∴BD⊥DF,
∴BD2+FD2=BF2,故选项B不合题意;
∵DG=GC,AE=EC,
∴EG∥AD,AD=2EG,
∴△EGO∽△DAO,
∴=()2=4,,
∴S△GEO=S△ADO,OE=DE=BD,故选项C符合题意,选项D不合题意,
故选:C.
二.填空题
11.解:添加一个条件OA=OC,则四边形ABCD为菱形,理由如下:
∵AC平分BD,OA=OC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形,
故答案为:OA=OC(答案不唯一).
12.解:已知AC=60cm,菱形对角线互相垂直平分,
∴AO=30cm,
又∵菱形ABCD周长为200cm,
∴AB=50cm,
∴BO===40cm,
∴AC=2BO=80cm,
∴菱形的面积为×60×80=2400(cm2).
故答案为:2400cm2.
13.解:∵菱形ABCD中,∠BAD=120°,
∴∠BAC=∠BAD=60°,AC⊥BD,
∴∠ABO=30°,
∵BD=6,
∴BO=3,
设AO=x,则AB=2x,
故x2+(3)2=(2x)2,
解得:x=3,
∴AO=3,
∴AC=6,
∴菱形的面积=6×6÷2=18.
故答案为:18.
14.解:如图,连接AC交BD于点G,连接AO,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD=10,BG=BD=8,
根据勾股定理得:AG===6,
∵S△ABD=S△AOB+S△AOD,
即BD?AG=AB?OE+AD?OF,
∴16×6=10OE+10OF,
∴OE+OF=9.6.
故答案为:9.6.
15.解:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=×6=3,
∵AB=5,
由勾股定理得:OB=4,
∴BD=2OB=8,
∵AB∥CD,
∴△EAB和△ECD的高的和等于点C到直线AB的距离,
∴△EAB和△ECD的面积和=×菱形ABCD的面积×==12.
故答案为:12
三.解答题
16.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:补充的条件是:AC⊥BD.
证明:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,
又∵AC⊥BD,
∴四边形AECF是菱形.
17.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB,
∴AB=CB,
∴?ABCD是菱形.
(2)解:由(1)得:?ABCD是菱形,
∴BC=AB=5,AO=CO,
∵AD∥BC,
∴∠AFE=∠CBE,
∵AE=AF=3,
∴∠AFE=∠AEF,
又∵∠AEF=∠CEB,
∴∠CBE=∠CEB,
∴CE=BC=5,
∴AC=AE+CE=3+5=8,
∴AO=AC=4.
18.(1)证明:∵AC垂直平分BD,
∴AB=AD,BC=CD,
∵BD平分∠ADC,
∴∠ADO=∠CDO,
又OD=OD,∠AOD=∠COD,
∴△AOD≌△COD(ASA),
∴AD=CD,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴AB∥CD,
∵BE∥CE,
∴四边形ACEB是平行四边形,
∴DC=AB=CE,
∴图中所有与△CBE面积相等的三角形有△BCD,△ABD,△ACD,△ABC.
一.选择题
1.如图,菱形ABCD中,∠A=50°,则∠ADB的度数为( )
A.65° B.55° C.45° D.25°
2.下列说法正确的是( )
A.对角线相等的四边形是菱形
B.四条边相等的四边形是菱形
C.一组邻边相等的四边形是菱形
D.对角线互相垂直的四边形是菱形
3.如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( )
A. B. C. D.
4.下列关系中,是菱形的性质但不是平行四边形的性质的是( )
A.对角线垂直 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
5.如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是( )
A.20° B.25° C.30° D.35°
6.如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A. B. C. D.
7.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当∠BAD=100°时,则∠CDF=( )
A.15° B.30° C.40° D.50°
8.如图,将菱形ABCD沿BD方向平移得到菱形EFGH,若FD:BF=1:3,菱形ABCD与菱形EFGH的重叠部分面积记为S1,菱形ABCD的面积记为S2,则S1:S2的值为( )
A.1:3 B.1:4 C.1:9 D.1:16
9.如图,在菱形ABCD中,E、F分别是AB、CD上的点,且AE=CF,EF与AC相交于点O,连接BO.若∠DAC=36°,则∠OBC的度数为( )
A.36° B.54° C.64° D.72°
10.如图,在菱形ABCD中,对角线AC,BD交于点E,延长BC到点F,使CF=BC,连接AF,DF,AF分别交CD,BD于点G,O,则下列结论错误的是( )
A.四边形ACFD是平行四边形
B.BD2+FD2=BF2
C.OE=BD
D.面积关系:S△GEO=S△ADO
二.填空题
11.如图,四边形ABCD的对角线AC与BD交于点O,AC⊥BD,且AC平分BD,若添加一个条件 ,则四边形ABCD为菱形.
12.若一个菱形的周长为200cm,一条对角线长为60cm,则它的面积为 .
13.菱形有一个内角为120°,较长的对角线长为6,则它的面积为 .
14.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF= .
15.如图,在菱形ABCD中,AC=6,AB=5,点E是直线AB、CD之间任意一点,连接AE、BE、DE、CE,则△EAB和△ECD的面积和等于 .
三.解答题
16.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F在BD上,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)不添加辅助线,请你补充一个条件,使得四边形AECF是菱形;并给予证明.
17.如图,已知?ABCD的对角线AC、BD交于点O,且∠1=∠2.
(1)求证:?ABCD是菱形.
(2)F为AD上一点,连接BF交AC于E,且AE=AF,若AF=3,AB=5,求AO的长.
18.在四边形ABCD中,对角线AC、BD相交于点O,且AC垂直平分BD,BD平分∠ADC.
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,过点B作BE∥AC,交DC延长线于点E,在不添加任何辅助线的情况下,请直接写出图中所有与△CBE面积相等的三角形(△CBE除外).
参考答案
一.选择题
1.解:∵四边形ABCD是菱形,
∴AB∥CD,∠ADB=∠CDB,
∴∠A+∠ADC=180°,
∵∠A=50°,
∴∠ADC=130°,
∴∠ADB=×130°=65°,
故选:A.
2.解:A.对角线相等的平行四边形是矩形,故不符合题意;
B.四条边相等的四边形是菱形,故符合题意;
C.一组邻边相等的平行四边形是菱形,故不符合题意;
D.对角线互相垂直的平行四边形是菱形,故不符合题意;
故选:B.
3.解:∵四边形ABCD是菱形,
∴CO=AC=3,BO=BD=4,AO⊥BO,
∴BC===5,
∵S菱形ABCD=AC?BD=BC×AE,
∴AE==.
在Rt△ABE中,BE===,
∴CE=BC﹣BE=5﹣=,
∴的值为,
故选:C.
4.解:A、菱形的对角线互相垂直平分、平行四边形的对角线互相平分,符合题意;
B、菱形、平行四边形的对边平行且相等,不符合题意;
C、菱形、平行四边形的对角线互相平分,不符合题意;
D、菱形、平行四边形的两组对角分别相等,不符合题意;
故选:A.
5.解:如图:
∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠HDO=∠DHO,
∵DH⊥CD,
∴∠GDO+∠ODC=90°,
∵BD⊥AC,
∴∠ODC+∠DCO=90°,
∴∠HDO=∠DCO,
∴∠DHO=∠DCA,
∵四边形ABCD是菱形,
∴DA=DC,
∴∠CAD=∠DCA=25°,
∴∠DHO=25°,
故选:B.
6.解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADB=∠ADC=60°,
∴△ABD是等边三角形,
∴AD=BD,
又∵△DEF是等边三角形,
∴∠EDF=∠DEF=60°,
又∵∠ADB=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,,
∴△ADE≌△BDF(ASA),
∴AE=BF,
∵AE=t,CF=2t,
∴BF=BC﹣CF=5﹣2t,
∴t=5﹣2t
∴t=,
故选:D.
7.解:如图,连接BF,
∵四边形ABCD是菱形,
∴CD=BC,∠DCF=∠BCF,
在△BCF和△DCF中,
∵,
∴△BCF≌△DCF(SAS)
∴∠CBF=∠CDF
∵FE垂直平分AB,∠BAF=×100°=50°
∴∠ABF=∠BAF=50°
∵∠ABC=180°﹣100°=80°,∠CBF=80°﹣50°=30°
∴∠CDF=30°.
故选:B.
8.解:如图设AD交EF于M,CD交FG于N.
由题意,重叠部分四边形MDNF是菱形,
菱形MFND∽菱形ABCD,
∴=()2,
∵DF:BF=1:3,
∴DF:BD=1:4,
∴=()2=,
故选:D.
9.解:∵四边形ABCD是菱形,
∴AB=BC=AD=CD,AB∥CD,AD∥BC,
∴∠EAO=∠FCO,∠DAC=∠ACB=36°,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AO=CO,
又∵AB=BC,
∴BO⊥AC,
∴∠OBC=90°﹣∠ACB=54°,
故选:B.
10.解:∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,AE=EC,BE=DE,AC⊥BD,
∵CF=BC,
∴CF=AD,
∴四边形ACFD是平行四边形,故选项A不合题意;
∴AC∥DF,DG=GC,
∴BD⊥DF,
∴BD2+FD2=BF2,故选项B不合题意;
∵DG=GC,AE=EC,
∴EG∥AD,AD=2EG,
∴△EGO∽△DAO,
∴=()2=4,,
∴S△GEO=S△ADO,OE=DE=BD,故选项C符合题意,选项D不合题意,
故选:C.
二.填空题
11.解:添加一个条件OA=OC,则四边形ABCD为菱形,理由如下:
∵AC平分BD,OA=OC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形,
故答案为:OA=OC(答案不唯一).
12.解:已知AC=60cm,菱形对角线互相垂直平分,
∴AO=30cm,
又∵菱形ABCD周长为200cm,
∴AB=50cm,
∴BO===40cm,
∴AC=2BO=80cm,
∴菱形的面积为×60×80=2400(cm2).
故答案为:2400cm2.
13.解:∵菱形ABCD中,∠BAD=120°,
∴∠BAC=∠BAD=60°,AC⊥BD,
∴∠ABO=30°,
∵BD=6,
∴BO=3,
设AO=x,则AB=2x,
故x2+(3)2=(2x)2,
解得:x=3,
∴AO=3,
∴AC=6,
∴菱形的面积=6×6÷2=18.
故答案为:18.
14.解:如图,连接AC交BD于点G,连接AO,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD=10,BG=BD=8,
根据勾股定理得:AG===6,
∵S△ABD=S△AOB+S△AOD,
即BD?AG=AB?OE+AD?OF,
∴16×6=10OE+10OF,
∴OE+OF=9.6.
故答案为:9.6.
15.解:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=×6=3,
∵AB=5,
由勾股定理得:OB=4,
∴BD=2OB=8,
∵AB∥CD,
∴△EAB和△ECD的高的和等于点C到直线AB的距离,
∴△EAB和△ECD的面积和=×菱形ABCD的面积×==12.
故答案为:12
三.解答题
16.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:补充的条件是:AC⊥BD.
证明:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是平行四边形,
又∵AC⊥BD,
∴四边形AECF是菱形.
17.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB,
∴AB=CB,
∴?ABCD是菱形.
(2)解:由(1)得:?ABCD是菱形,
∴BC=AB=5,AO=CO,
∵AD∥BC,
∴∠AFE=∠CBE,
∵AE=AF=3,
∴∠AFE=∠AEF,
又∵∠AEF=∠CEB,
∴∠CBE=∠CEB,
∴CE=BC=5,
∴AC=AE+CE=3+5=8,
∴AO=AC=4.
18.(1)证明:∵AC垂直平分BD,
∴AB=AD,BC=CD,
∵BD平分∠ADC,
∴∠ADO=∠CDO,
又OD=OD,∠AOD=∠COD,
∴△AOD≌△COD(ASA),
∴AD=CD,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴AB∥CD,
∵BE∥CE,
∴四边形ACEB是平行四边形,
∴DC=AB=CE,
∴图中所有与△CBE面积相等的三角形有△BCD,△ABD,△ACD,△ABC.
