2020-2021学年 苏科版七年级数学下册 7.4认识三角形提优训练试卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年 苏科版七年级数学下册 7.4认识三角形提优训练试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 815.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览



文档简介
7.4 认识三角形 提优训练
一、单选题
1.(2021·安徽安庆市·八年级期末)下列命题中,属于真命题的是( )
A.一个三角形至少有两个内角是锐角 B.一个角的补角大于这个角
C.内错角相等 D.相等的角是对顶角
2.(2021·湖北孝感市·八年级期末)下列各组线段,能构成三角形的是( )
A. B. C. D.
3.(2021·云南红河哈尼族彝族自治州·八年级期末)如图,直线,则等于( )
A. B. C. D.
4.(2020·河北邯郸市·育华中学七年级月考)如图,∠ABC=90°,BD⊥AC,下列关系式中不一定成立的是( )
A.AB>AD B.AC>BC C.BD+CD>BC D.CD>BD
5.(2021·西安市曲江第一中学八年级期末)如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为( )
A.32° B.30° C.28° D.26°
6.(2020·涿州市实验中学八年级期中)下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B﹣∠C,则△ABC为直角三角形
C.在△ABC中,若∠A=∠B=∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
7.(2020·浙江杭州市·八年级期末)如图,在△ABC中,已知点D,E,F分别为边AC,BD,CE的中点,且阴影部分图形面积等于4平方厘米,则△ABC的面积为( )平方厘米
A.8 B.12 C.16 D.18
8.(2020·浙江八年级开学考试)如图,在中,,与的角平分线交于,与的角平分线交于点,依此类推,与的角平分线交于点,则的度数是( )
A. B. C. D.
9.(2020·三台县潼川初级中学校八年级月考)若a,b,c是△ABC的三边,则化简的结果是( )
A. B.
C. D.0
10.(2020·北京八中乌兰察布分校八年级月考)如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )
A.180° B.360° C.540° D.720°
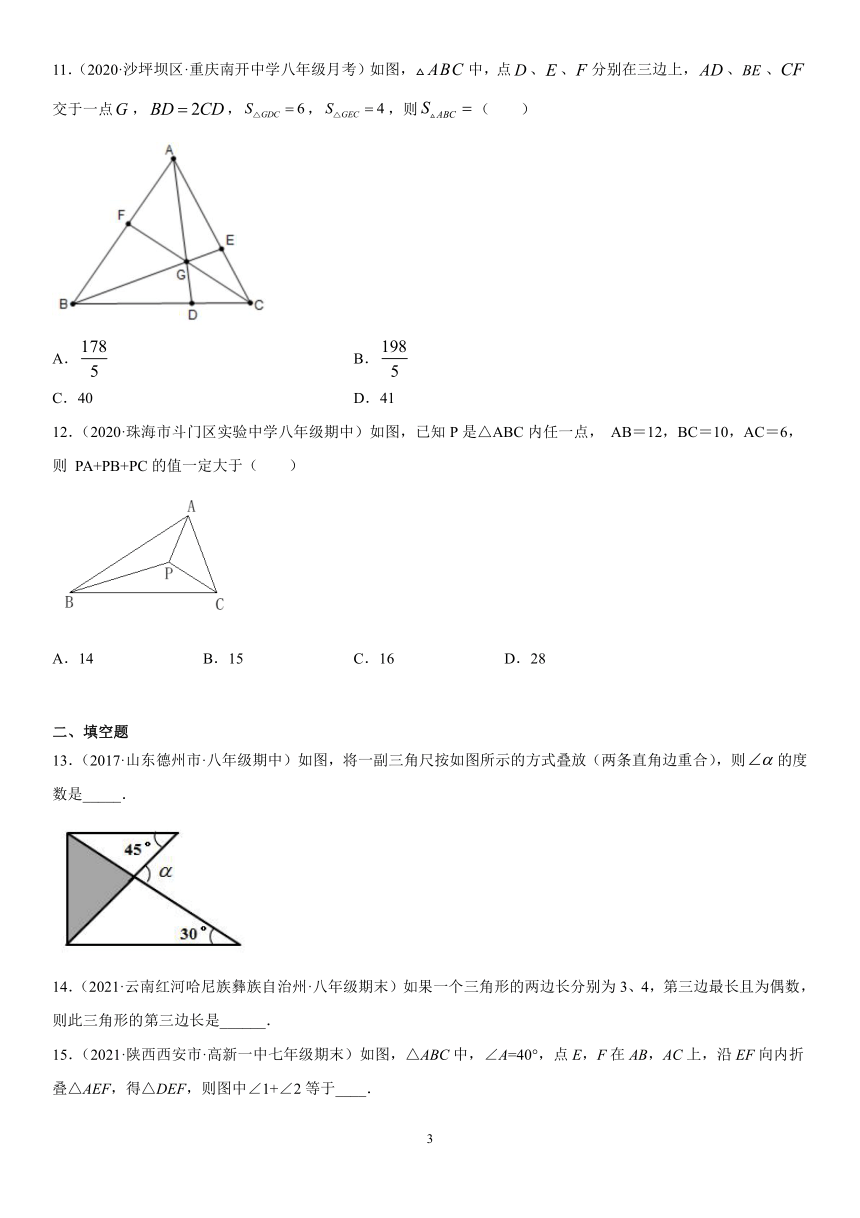
11.(2020·沙坪坝区·重庆南开中学八年级月考)如图,中,点、、分别在三边上,、、交于一点,,,,则( )
A. B.
C.40 D.41
12.(2020·珠海市斗门区实验中学八年级期中)如图,已知P是△ABC内任一点, AB=12,BC=10,AC=6,则 PA+PB+PC的值一定大于( )
A.14 B.15 C.16 D.28
二、填空题
13.(2017·山东德州市·八年级期中)如图,将一副三角尺按如图所示的方式叠放(两条直角边重合),则的度数是_____.
14.(2021·云南红河哈尼族彝族自治州·八年级期末)如果一个三角形的两边长分别为3、4,第三边最长且为偶数,则此三角形的第三边长是______.
15.(2021·陕西西安市·高新一中七年级期末)如图,△ABC中,∠A=40°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于____.
16.(2021·辽宁鞍山市·八年级期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=_____.
17.(2021·福州三牧中学七年级期末)如图,已知AB∥CD,AE、CE分别甲分∠FAB,∠FCD,∠F=a,则∠E=_________,(用含a的式子表示)
18.(2020·四川成都市·西川中学南区七年级期中)如图,,,,为上一点,且,在直线上取一点,使,则的值为__________.
19.(2021·辽宁鞍山市·八年级期中)如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为_____.
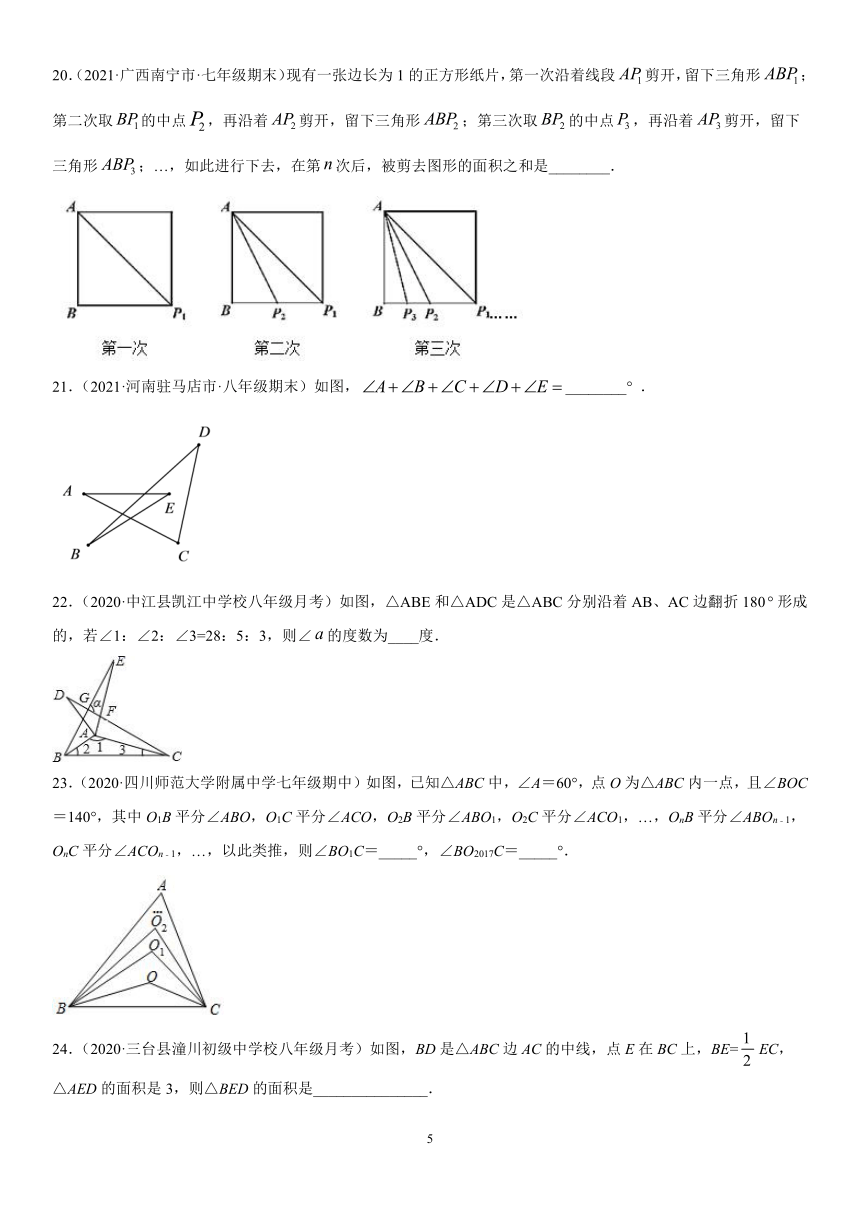
20.(2021·广西南宁市·七年级期末)现有一张边长为1的正方形纸片,第一次沿着线段剪开,留下三角形;第二次取的中点,再沿着剪开,留下三角形;第三次取的中点,再沿着剪开,留下三角形;…,如此进行下去,在第次后,被剪去图形的面积之和是________.
21.(2021·河南驻马店市·八年级期末)如图,________° .
22.(2020·中江县凯江中学校八年级月考)如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180形成的,若∠1:∠2:∠3=28:5:3,则∠的度数为____度.
23.(2020·四川师范大学附属中学七年级期中)如图,已知△ABC中,∠A=60°,点O为△ABC内一点,且∠BOC=140°,其中O1B平分∠ABO,O1C平分∠ACO,O2B平分∠ABO1,O2C平分∠ACO1,…,OnB平分∠ABOn﹣1,OnC平分∠ACOn﹣1,…,以此类推,则∠BO1C=_____°,∠BO2017C=_____°.
24.(2020·三台县潼川初级中学校八年级月考)如图,BD是△ABC边AC的中线,点E在BC上,BE=EC,△AED的面积是3,则△BED的面积是_______________.
三、解答题
25.(2020·河北张家口市·八年级期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=72°,∠C=30°,
①求∠BAE的度数;
②求∠DAE的度数.
26.(2020·太原市·山西实验中学八年级月考)证明:三角形内角和.(画出图形,写出已知、求证,并证明)
27.(2020·浙江杭州市·八年级期末)如图,在中,是边上的高线,的垂直平分线分别交,于点,.
(1)若,求的度数;
(2)试判断与的数量关系,并说明理由.
28.(2020·浙江省义乌市望道中学七年级月考)已知,下列各图中的、、三个角之间各有什么关系?填入下列括号内,并选择一个你自己喜欢的图加以说明理由.
解:(1)图结论:____________________________;
(2)图结论:____________________________;
(3)图结论:____________________________;
(4)图结论:____________________________;
29.(2021·铜川市第一中学八年级期末)如图,在中,于点, 交于点,于点,交 于点.
(1)求证:;
(2)若,,求 的度数.
30.(2021·山东枣庄市·八年级期末)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为_____°,△AOB_______.(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC_______(填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
31.(2020·武汉市江夏区大方学校七年级月考)如图1,AB∥CD,E,F分别是直线AB和CD上的两点,点P在直线AB,CD之间.
(1)求证:∠AEP+∠CFP=∠EPF;
(2)如图2,反向延长EP至G点,∠GEB和∠PFD的平分线交于Q点,若∠P+∠Q=130°,求∠Q的度数;
(3)如图3,M是射线EG上一动点,MK平分∠PMF,FN平分∠MFD,过F作FJ∥MK,请直接写出∠JFN和∠BEP的数量关系.
32.(2020·哈尔滨市虹桥初级中学校七年级月考)已知:在ABC中,∠ABC=∠ACB,BD是ABC的高.
(1)如图1,当∠BAC=50°时,求∠DBC的度数.
(2)如图2,当∠BAC>90°时,请你判断∠DBC与∠BAC的关系,并证明你的结论.
(3)如图3,在(2)的条件下,作BE平分∠DBA交CD于点E,CF平分∠ACB,连接EF,若∠FEB=90°﹣∠BEC,求∠F度数.
参考答案
1.A 2.C 3.B 4.D 5.C 6.D 7.C 8.B 9.B 10.C
11.B 12.A
13. 14.6 15.80° 16.50°. 17. 18.或 19.70°.
20.1- 21.180 22.80° 23.100 [60+()2017×80]. 24.
25.①∠BAE=39°;②∠DAE=21°.
【详解】
解:①∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣72°﹣30°=78°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=39°;
②∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=18°,
∴∠DAE=∠BAE﹣∠BAD=39°﹣18°=21°.
26.见解析.
【详解】
已知:如图,
求证:
证明:过点作,如图,
三角形内角和.
27.(1);(2),证明见解析
【详解】
(1)如图,
∵,为的垂直平分线,
∴,,
∴,
又∵是边上的高线,
∴,
∴;
(2)∵,,
∴,
∴,
又∵为的垂直平分线,
∴,
∵,
∴.
28.(1)∠ABE+∠CDE+∠BED=360°;(2)∠ABE+∠CDE=∠BED;(3)∠ABE=∠CDE+∠E;(4)∠CDE=∠ABE+∠E
【详解】
解:若选图(1),过点E作EF∥CD,
∵AB∥CD,∴AB∥EF,
∴∠CDE+∠DEF=180°,∠ABE+∠BEF=180°,
∴∠ABE+∠CDE+∠BED=360°;
若选图(2),过点E作EF∥CD,
∵AB∥CD,∴AB∥EF,
∴∠CDE=∠DEF,∠ABE=∠BEF,
∴∠ABE+∠CDE=∠DEF+∠BEF=∠BED;
若选图(3),∵AB∥CD,
∴∠ABE=∠CFE=∠E+∠CDE;
若选图(4),∵AB∥CD,
∴∠ABE=∠CFE,
∴∠CDE=∠ABE+∠E.
29.(1)证明见详解;(2).
【详解】
(1)证明:,
,
,,
,
,
;
(2)解:,,
,
,
,
.
30.(1)30;是;(2)是;(3)30°或52.5°或80°.
【详解】
解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①当∠ACB=3∠ABC时,∵∠ABO=30°,
∴∠ACB=90°,
∴∠CAB=60°,
∴∠OAC=30°;
②当∠ABC=3∠CAB时,
∵∠ABO=30°,
∴∠CAB=10°,
∵∠OAB=90°,
∴∠OAC=80°.
③当∠ACB=3∠CAB时,
∵∠ABO=30°,
∴4∠CAB=150°,
∴∠CAB=37.5°,
∴∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
31.(1)证明见详解;(2)∠Q=50°;(3)结论:2∠JFN+∠BEP=180°.证明见详解.
【详解】
解:(1)过点P作PG∥AB,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠EPG,∠CFP=∠GPF,
∴∠EPF=∠EPG+∠FPG=∠AEP+∠CFP;
,
(2)设∠AEP=,∠CFP=,FQ交AB于H,
∵∠QHB=∠Q+∠QEB,
∴∠Q=∠QHB-∠QEB,
∵∠AEP=∠GEB=,∠PFD=180°-,
∵AB∥CD,
∴∠QHB=∠QFD,
∵∠GEB和∠PFD的平分线交于Q点,
∴∠QEB=,∠QFD=,
∴∠Q=∠QHB-∠QEB=-=90°-=90°-,
即∠Q+=90°,
而∠Q+=130°,
∴,
解得,
∴∠Q=50°;
(3)结论:2∠JFN+∠BEP=180°.
设FM与AB交H,
∵MK平分∠PMF,FN平分∠MFD,
∴∠KMH=,∠HFN=,
∵FJ∥MK,
∴∠KMH=∠HFJ,
∵∠PEB=∠EMH+∠EHM=∠EMH+∠FHB=∠EMH+180°-∠HFD,
∴∠PEB=∠EMH+180°-∠HFD=+180°-2∠HFN=+180°-2 =180°-2(∠HFN-),
∴∠PEB=180°-2(∠HFN-)=180°-2∠JFN,
∴2∠JFN+∠BEP=180°.
32.(1)25°;(2)2∠DBC=∠BAC,见解析;(3)22.5°
【详解】
(1)∵∠ABC=∠ACB,∠BAC=50°,
∴∠ABC=(180°-50°)=65°,
∵BD是△ABC的高,
∴∠ABD=90°﹣50°=40°,
∴∠DBC=65°﹣40°=25°;
(2)2∠DBC=∠BAC,理由如下:
∵∠ABC=∠ACB,
∴∠DAB=2∠ABC=180°﹣∠BAC,
∵BD是△ABC的高,
∴∠DBA=90°﹣∠DAB=90°﹣2∠ABC,
∴∠DBC=∠DBA+∠ABC=90°﹣2∠ABC+∠ABC=90°﹣∠ABC,
∴∠DBC=90°-(180°-∠BAC)=;
即2∠DBC=∠BAC;
(3)设∠DBC=α,则∠BAC=2α,
∵BE平分∠DBA,设∠DBE=∠EBA=β,
在△ABD中,∠BAC=∠DBA+90°=2β+90°=2α,
则β=α﹣45°=∠EBA,
在△BDC中,∠BCD=90°﹣∠DBC=90°﹣α,
∴∠FCE=∠FCB=(90°﹣α)=45°﹣,
在△EFC中,∵∠FEB=90°﹣∠BEC,则∠FEC=90°+∠BEC,
在△ABE中,∠BAC=∠BEC+∠EBA=∠BEC+α﹣45°=2α,
则∠BEC=45°+α,
则∠FEC=90°+∠BEC=90°+(45°+α)=112.5°+α,
而∠FCE=45°﹣α,
则∠F=180°﹣(∠FEC+∠FCE)=180°﹣(112.5°+α+45°﹣α)=22.5°.
一、单选题
1.(2021·安徽安庆市·八年级期末)下列命题中,属于真命题的是( )
A.一个三角形至少有两个内角是锐角 B.一个角的补角大于这个角
C.内错角相等 D.相等的角是对顶角
2.(2021·湖北孝感市·八年级期末)下列各组线段,能构成三角形的是( )
A. B. C. D.
3.(2021·云南红河哈尼族彝族自治州·八年级期末)如图,直线,则等于( )
A. B. C. D.
4.(2020·河北邯郸市·育华中学七年级月考)如图,∠ABC=90°,BD⊥AC,下列关系式中不一定成立的是( )
A.AB>AD B.AC>BC C.BD+CD>BC D.CD>BD
5.(2021·西安市曲江第一中学八年级期末)如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为( )
A.32° B.30° C.28° D.26°
6.(2020·涿州市实验中学八年级期中)下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B﹣∠C,则△ABC为直角三角形
C.在△ABC中,若∠A=∠B=∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
7.(2020·浙江杭州市·八年级期末)如图,在△ABC中,已知点D,E,F分别为边AC,BD,CE的中点,且阴影部分图形面积等于4平方厘米,则△ABC的面积为( )平方厘米
A.8 B.12 C.16 D.18
8.(2020·浙江八年级开学考试)如图,在中,,与的角平分线交于,与的角平分线交于点,依此类推,与的角平分线交于点,则的度数是( )
A. B. C. D.
9.(2020·三台县潼川初级中学校八年级月考)若a,b,c是△ABC的三边,则化简的结果是( )
A. B.
C. D.0
10.(2020·北京八中乌兰察布分校八年级月考)如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )
A.180° B.360° C.540° D.720°
11.(2020·沙坪坝区·重庆南开中学八年级月考)如图,中,点、、分别在三边上,、、交于一点,,,,则( )
A. B.
C.40 D.41
12.(2020·珠海市斗门区实验中学八年级期中)如图,已知P是△ABC内任一点, AB=12,BC=10,AC=6,则 PA+PB+PC的值一定大于( )
A.14 B.15 C.16 D.28
二、填空题
13.(2017·山东德州市·八年级期中)如图,将一副三角尺按如图所示的方式叠放(两条直角边重合),则的度数是_____.
14.(2021·云南红河哈尼族彝族自治州·八年级期末)如果一个三角形的两边长分别为3、4,第三边最长且为偶数,则此三角形的第三边长是______.
15.(2021·陕西西安市·高新一中七年级期末)如图,△ABC中,∠A=40°,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于____.
16.(2021·辽宁鞍山市·八年级期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=_____.
17.(2021·福州三牧中学七年级期末)如图,已知AB∥CD,AE、CE分别甲分∠FAB,∠FCD,∠F=a,则∠E=_________,(用含a的式子表示)
18.(2020·四川成都市·西川中学南区七年级期中)如图,,,,为上一点,且,在直线上取一点,使,则的值为__________.
19.(2021·辽宁鞍山市·八年级期中)如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为_____.
20.(2021·广西南宁市·七年级期末)现有一张边长为1的正方形纸片,第一次沿着线段剪开,留下三角形;第二次取的中点,再沿着剪开,留下三角形;第三次取的中点,再沿着剪开,留下三角形;…,如此进行下去,在第次后,被剪去图形的面积之和是________.
21.(2021·河南驻马店市·八年级期末)如图,________° .
22.(2020·中江县凯江中学校八年级月考)如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180形成的,若∠1:∠2:∠3=28:5:3,则∠的度数为____度.
23.(2020·四川师范大学附属中学七年级期中)如图,已知△ABC中,∠A=60°,点O为△ABC内一点,且∠BOC=140°,其中O1B平分∠ABO,O1C平分∠ACO,O2B平分∠ABO1,O2C平分∠ACO1,…,OnB平分∠ABOn﹣1,OnC平分∠ACOn﹣1,…,以此类推,则∠BO1C=_____°,∠BO2017C=_____°.
24.(2020·三台县潼川初级中学校八年级月考)如图,BD是△ABC边AC的中线,点E在BC上,BE=EC,△AED的面积是3,则△BED的面积是_______________.
三、解答题
25.(2020·河北张家口市·八年级期中)如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=72°,∠C=30°,
①求∠BAE的度数;
②求∠DAE的度数.
26.(2020·太原市·山西实验中学八年级月考)证明:三角形内角和.(画出图形,写出已知、求证,并证明)
27.(2020·浙江杭州市·八年级期末)如图,在中,是边上的高线,的垂直平分线分别交,于点,.
(1)若,求的度数;
(2)试判断与的数量关系,并说明理由.
28.(2020·浙江省义乌市望道中学七年级月考)已知,下列各图中的、、三个角之间各有什么关系?填入下列括号内,并选择一个你自己喜欢的图加以说明理由.
解:(1)图结论:____________________________;
(2)图结论:____________________________;
(3)图结论:____________________________;
(4)图结论:____________________________;
29.(2021·铜川市第一中学八年级期末)如图,在中,于点, 交于点,于点,交 于点.
(1)求证:;
(2)若,,求 的度数.
30.(2021·山东枣庄市·八年级期末)在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为_____°,△AOB_______.(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC_______(填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
31.(2020·武汉市江夏区大方学校七年级月考)如图1,AB∥CD,E,F分别是直线AB和CD上的两点,点P在直线AB,CD之间.
(1)求证:∠AEP+∠CFP=∠EPF;
(2)如图2,反向延长EP至G点,∠GEB和∠PFD的平分线交于Q点,若∠P+∠Q=130°,求∠Q的度数;
(3)如图3,M是射线EG上一动点,MK平分∠PMF,FN平分∠MFD,过F作FJ∥MK,请直接写出∠JFN和∠BEP的数量关系.
32.(2020·哈尔滨市虹桥初级中学校七年级月考)已知:在ABC中,∠ABC=∠ACB,BD是ABC的高.
(1)如图1,当∠BAC=50°时,求∠DBC的度数.
(2)如图2,当∠BAC>90°时,请你判断∠DBC与∠BAC的关系,并证明你的结论.
(3)如图3,在(2)的条件下,作BE平分∠DBA交CD于点E,CF平分∠ACB,连接EF,若∠FEB=90°﹣∠BEC,求∠F度数.
参考答案
1.A 2.C 3.B 4.D 5.C 6.D 7.C 8.B 9.B 10.C
11.B 12.A
13. 14.6 15.80° 16.50°. 17. 18.或 19.70°.
20.1- 21.180 22.80° 23.100 [60+()2017×80]. 24.
25.①∠BAE=39°;②∠DAE=21°.
【详解】
解:①∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣72°﹣30°=78°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=39°;
②∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=18°,
∴∠DAE=∠BAE﹣∠BAD=39°﹣18°=21°.
26.见解析.
【详解】
已知:如图,
求证:
证明:过点作,如图,
三角形内角和.
27.(1);(2),证明见解析
【详解】
(1)如图,
∵,为的垂直平分线,
∴,,
∴,
又∵是边上的高线,
∴,
∴;
(2)∵,,
∴,
∴,
又∵为的垂直平分线,
∴,
∵,
∴.
28.(1)∠ABE+∠CDE+∠BED=360°;(2)∠ABE+∠CDE=∠BED;(3)∠ABE=∠CDE+∠E;(4)∠CDE=∠ABE+∠E
【详解】
解:若选图(1),过点E作EF∥CD,
∵AB∥CD,∴AB∥EF,
∴∠CDE+∠DEF=180°,∠ABE+∠BEF=180°,
∴∠ABE+∠CDE+∠BED=360°;
若选图(2),过点E作EF∥CD,
∵AB∥CD,∴AB∥EF,
∴∠CDE=∠DEF,∠ABE=∠BEF,
∴∠ABE+∠CDE=∠DEF+∠BEF=∠BED;
若选图(3),∵AB∥CD,
∴∠ABE=∠CFE=∠E+∠CDE;
若选图(4),∵AB∥CD,
∴∠ABE=∠CFE,
∴∠CDE=∠ABE+∠E.
29.(1)证明见详解;(2).
【详解】
(1)证明:,
,
,,
,
,
;
(2)解:,,
,
,
,
.
30.(1)30;是;(2)是;(3)30°或52.5°或80°.
【详解】
解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①当∠ACB=3∠ABC时,∵∠ABO=30°,
∴∠ACB=90°,
∴∠CAB=60°,
∴∠OAC=30°;
②当∠ABC=3∠CAB时,
∵∠ABO=30°,
∴∠CAB=10°,
∵∠OAB=90°,
∴∠OAC=80°.
③当∠ACB=3∠CAB时,
∵∠ABO=30°,
∴4∠CAB=150°,
∴∠CAB=37.5°,
∴∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
31.(1)证明见详解;(2)∠Q=50°;(3)结论:2∠JFN+∠BEP=180°.证明见详解.
【详解】
解:(1)过点P作PG∥AB,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠EPG,∠CFP=∠GPF,
∴∠EPF=∠EPG+∠FPG=∠AEP+∠CFP;
,
(2)设∠AEP=,∠CFP=,FQ交AB于H,
∵∠QHB=∠Q+∠QEB,
∴∠Q=∠QHB-∠QEB,
∵∠AEP=∠GEB=,∠PFD=180°-,
∵AB∥CD,
∴∠QHB=∠QFD,
∵∠GEB和∠PFD的平分线交于Q点,
∴∠QEB=,∠QFD=,
∴∠Q=∠QHB-∠QEB=-=90°-=90°-,
即∠Q+=90°,
而∠Q+=130°,
∴,
解得,
∴∠Q=50°;
(3)结论:2∠JFN+∠BEP=180°.
设FM与AB交H,
∵MK平分∠PMF,FN平分∠MFD,
∴∠KMH=,∠HFN=,
∵FJ∥MK,
∴∠KMH=∠HFJ,
∵∠PEB=∠EMH+∠EHM=∠EMH+∠FHB=∠EMH+180°-∠HFD,
∴∠PEB=∠EMH+180°-∠HFD=+180°-2∠HFN=+180°-2 =180°-2(∠HFN-),
∴∠PEB=180°-2(∠HFN-)=180°-2∠JFN,
∴2∠JFN+∠BEP=180°.
32.(1)25°;(2)2∠DBC=∠BAC,见解析;(3)22.5°
【详解】
(1)∵∠ABC=∠ACB,∠BAC=50°,
∴∠ABC=(180°-50°)=65°,
∵BD是△ABC的高,
∴∠ABD=90°﹣50°=40°,
∴∠DBC=65°﹣40°=25°;
(2)2∠DBC=∠BAC,理由如下:
∵∠ABC=∠ACB,
∴∠DAB=2∠ABC=180°﹣∠BAC,
∵BD是△ABC的高,
∴∠DBA=90°﹣∠DAB=90°﹣2∠ABC,
∴∠DBC=∠DBA+∠ABC=90°﹣2∠ABC+∠ABC=90°﹣∠ABC,
∴∠DBC=90°-(180°-∠BAC)=;
即2∠DBC=∠BAC;
(3)设∠DBC=α,则∠BAC=2α,
∵BE平分∠DBA,设∠DBE=∠EBA=β,
在△ABD中,∠BAC=∠DBA+90°=2β+90°=2α,
则β=α﹣45°=∠EBA,
在△BDC中,∠BCD=90°﹣∠DBC=90°﹣α,
∴∠FCE=∠FCB=(90°﹣α)=45°﹣,
在△EFC中,∵∠FEB=90°﹣∠BEC,则∠FEC=90°+∠BEC,
在△ABE中,∠BAC=∠BEC+∠EBA=∠BEC+α﹣45°=2α,
则∠BEC=45°+α,
则∠FEC=90°+∠BEC=90°+(45°+α)=112.5°+α,
而∠FCE=45°﹣α,
则∠F=180°﹣(∠FEC+∠FCE)=180°﹣(112.5°+α+45°﹣α)=22.5°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
