2020-2021学年 苏科版七年级数学下册 7.5多边形的内角和与外角和提优训练(word版含答案)
文档属性
| 名称 | 2020-2021学年 苏科版七年级数学下册 7.5多边形的内角和与外角和提优训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览



文档简介
7.5 多边形的内角和与外角和 提优训练
一、单选题
1.(2021·江苏苏州市·九年级零模)一个n边形的每个外角都是45°,则这个n边形的内角和是( )
A.1080° B.540° C.2700° D.2160°
2.(2021·广西河池市·八年级期末)已知一个边形的每一个外角都相等,一个内角与其相邻的一个外角的度数之比是,则的值是( )
A.8 B.9 C.10 D.12
3.(2021·河北廊坊市·八年级期末)如图,等于( )
A.360° B.335° C.385° D.405°
4.(2020·四川省自贡市贡井区成佳中学校八年级月考)将一个五边形纸片的一个角剪去,所得多边形的内角和不可能是( )
A.180° B.360° C.540° D.720°
5.(2021·安徽阜阳市·八年级期末)如果一个多边形的内角和为,那么从这个多边形的一个顶点可以作( )条对角线.
A. B. C. D.
6.(2020·武汉市六中位育中学八年级)如图,在四边形中,,分别是两组对边延长线的交点,,分别是,的角平分线.若,,则( )
A. B. C. D.
7.(2021·山东东营市·八年级期末)如图,用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE,其中∠BAE的度数是( )
A.90° B.108° C.120° D.135°
8.(2021·河北唐山市·八年级期末)一个多边形截去一个角后,形成的另一个多边形的内角和是,则原来多边形的边数是( )
A. B. C.或 D.或或
9.(2019·莆田第十五中学八年级月考)如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请你试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=∠1+∠2 D.3∠A=2(∠1+∠2)
10.(2020·江苏无锡市·七年级期中)图1是二环三角形,S=∠A1+∠A2+…+∠A6=360,图2是二环四边形,S=∠A1+∠A2+…+∠A=720,图3是二环五边形,S=∠A1+∠A2+…+∠A=1080…聪明的同学,请你直接写出二环十边形,S=_____________度( )
A.1440 B.1800 C.2880 D.3600
二、填空题
11.(2020·浙江杭州市·八年级期末)若十二边形的每一个内角都相等,那么它每个内角的度数是____________.
12.(2021·广东汕尾市·九年级期末)如图,的度数为__________.
13.(2018·四川成都市·成都实外八年级开学考试)的两边分别垂直于的两边,且的度数比的度数的2倍少24°,则、的度数分别是____________.
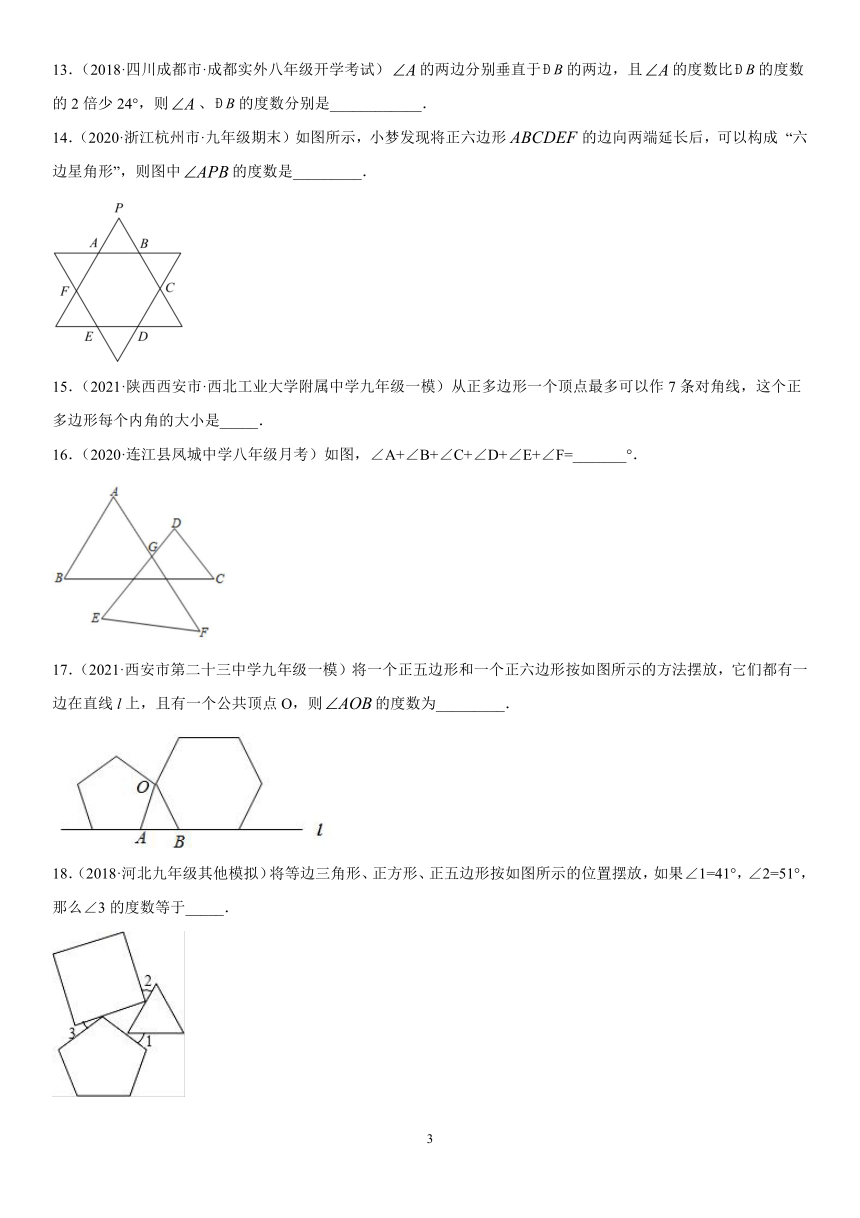
14.(2020·浙江杭州市·九年级期末)如图所示,小梦发现将正六边形的边向两端延长后,可以构成 “六边星角形”,则图中的度数是_________.
15.(2021·陕西西安市·西北工业大学附属中学九年级一模)从正多边形一个顶点最多可以作7条对角线,这个正多边形每个内角的大小是_____.
16.(2020·连江县凤城中学八年级月考)如图,∠A+∠B+∠C+∠D+∠E+∠F=_______°.
17.(2021·西安市第二十三中学九年级一模)将一个正五边形和一个正六边形按如图所示的方法摆放,它们都有一边在直线l上,且有一个公共顶点O,则的度数为_________.
18.(2018·河北九年级其他模拟)将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=41°,∠2=51°,那么∠3的度数等于_____.
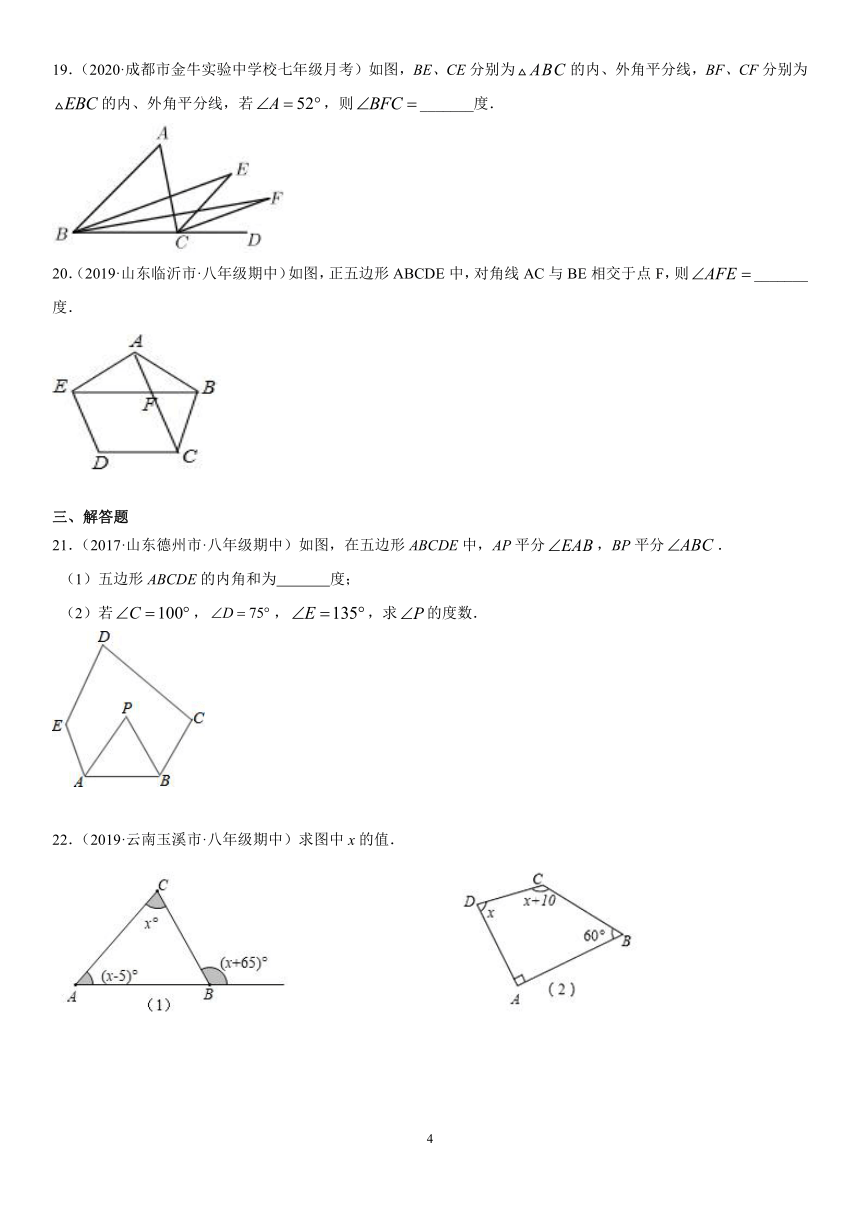
19.(2020·成都市金牛实验中学校七年级月考)如图,BE、CE分别为的内、外角平分线,BF、CF分别为的内、外角平分线,若,则_______度.
20.(2019·山东临沂市·八年级期中)如图,正五边形ABCDE中,对角线AC与BE相交于点F,则_______度.
三、解答题
21.(2017·山东德州市·八年级期中)如图,在五边形ABCDE中,AP平分,BP平分.
(1)五边形ABCDE的内角和为 度;
(2)若,,,求的度数.
22.(2019·云南玉溪市·八年级期中)求图中x的值.
23.(2020·海南省直辖县级行政单位·八年级期中)一个多边形的每一个外角都等于.
(1)求这个多边形的边数;
(2)求这个多边形对角线的条数.
24.(2021·全国八年级)若边形的内角和等于它外角和的倍,求边数.
已知,,为三角形三边的长,化简:.
25.(2020·内蒙古赤峰市·八年级期中)阅读材料
在平面中,我们把大于且小于的角称为优角.如果两个角相加等于,那么称这两个角互为组角,简称互组.
(1)若,互为组角,且,则______.
习惯上,我们把有一个内角大于的四边形俗称为镖形.
(2)如图,在镖形ABCD中,优角与钝角互为组角,试探索内角,,与钝角之间的数量关系,并至少用两种以上的方法说明理由.
26.(2021·黑龙江哈尔滨市·八年级期末)已知在四边形ABCD中,.
(1)如图1,若BE平分,DF平分的邻补角,请写出BE与DF的位置关系并证明;
(2)如图2,若BF、DE分别平分、的邻补角,判断DE与BF位置关系并证明;
(3)如图3,若BE、DE分别五等分、的邻补角(即),求度数.
27.(2020·安徽阜阳市·八年级期中)在中,,点D、E分别是边AC、BC(不与A、B、C重合)上的点,(P与D、E不在同一条战线上),令,,.
(1)若点P在边AB上,如图(1)且,则________°;
(2)若点P在的外部如图(2)则,,之间有何关系?
(3)若点P在边BA的延长线上运动(),直接写出,,之间的关系.
28.(2020·玉山县南山乡中学八年级月考)我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图中,的内角与的内角互为对顶角,则与为对顶三角形,根据三角形内角和定理知“对顶三角形”有如下性质:.
性质理解:如图,在“对顶三角形”与中,,,求证:;
性质应用:
①如图,则的度数为________;
②如图,在中,点,分别在,上,若比大,求的度数;
拓展提高:
如图,已知,是的角平分线,且和的平分线和相交于点,设,求的度数(用表示).
参考答案
1.A 2.B 3.C 4.A 5.C 6.D 7.B 8.D 9.B 10.C
11.150° 12. 13.,或 14.60°
15.144° 16.360 17.84° 18.10° 19.13 20.72.
21.(1)540;(2)65°
【详解】
解:(1)五边形ABCDE的内角和为,
(2)∵在五边形ABCDE中,,
,,
∴,
∵AP平分,BP平分,
∴,,
∴,
∴.
22.(1)70°;(2)100°
【详解】
解:(1)由三角形外角等于与它不相邻的两个内角的和,得x+65=x+x-5,
解得:x=70°,
(2)由四边形内角和等于360°,得x+x+10°+60°+90°=360°
解得:x=100°.
23.(1)12;(2)54
【详解】
解:(1),
答:这个多边形的边数为;
(2)(条).
答:这个多边形的对角线的条数是条.
24.8;.
【详解】
解:由题意得:,
解得:.
∵,,为三角形三边的长,
∴,,
∴.
25.(1)225°;(2)钝角∠BCD=∠A+∠B+∠D,理由见解析.
【详解】
解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°-∠1=225°,
故答案为:225°;
(2)钝角∠BCD=∠A+∠B+∠D.
理由如下:
理由①:∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360°?,
∴钝角∠BCD=∠A+∠B+∠D;
理由②:如下图,连接AC并延长,
∵∠BAC+∠B=∠BCE,∠DAC+∠D=∠DCE(三角形外角的性质),
∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D.
26.(1),证明见解析;(2),证明见解析;(3)54°
【详解】
(1).
证明:延长BE、FD交于G.在四边形ABCD中,
,,
.
,.
平分,DF平分,
,,
,
∵∠ABE+∠AEB=90°,∠AEB=∠DEG,∠FDN=∠EDG,
∴∠DEG+∠EDG=90°,
∴∠EGD=90°,即BE⊥DF.
(2).
证明:连接DB.
,.
又,.
、DF平分、的邻补角,
,,
.
在中,
,
,
,.
(3)延长DC交BE于H.由(1)得:
.
、DE分别五等分、的邻补角,
,
由三角形的外角性质得,
,,
,
.
27.(1)120;(2)∠2-∠1=∠α-80°;(3)∠2-∠1=∠α+80°或∠2-∠1=80°-∠α
【详解】
解:(1)∵∠CEP=180°-∠2,∠CDP=180°-∠1,
∴180°-∠2+180°-∠1+∠α+80°=360°,
即∠1+∠2=80°+∠α,
∵α=40°,
∴∠1+∠2=120°.
故答案为:120.
(2)根据三角形外角的性质可知,
∠2-∠α=∠1-80°,
则∠2-∠1=∠α-80°.
(3)①如图3,
∠2=80°+∠1+∠α,
则∠2-∠1=∠α+80°;
②如图4,
∠1=∠α+∠DFP=∠α+∠CFE,
∠2=80°+∠CFE,
∴∠1=∠α+∠2-80°,
即∠2-∠1=80°-∠α.
28.(1)见解析;(2)①180°;②100°;(3)
【详解】
(1)证明:据题意,得,
∴,
∵,,
∴;
(2)解:①
;
故答案为:;
②由题意得,
由(1)得,
∴,
∵,
∴,
故,
∵,
∴,
∴,
∵,
∴;
(3)解:,
理由如下:
∵和的平分线和相交于点,
∴,,
由(1)得①,
②,
由①②得,
∴,
即,
∴.
一、单选题
1.(2021·江苏苏州市·九年级零模)一个n边形的每个外角都是45°,则这个n边形的内角和是( )
A.1080° B.540° C.2700° D.2160°
2.(2021·广西河池市·八年级期末)已知一个边形的每一个外角都相等,一个内角与其相邻的一个外角的度数之比是,则的值是( )
A.8 B.9 C.10 D.12
3.(2021·河北廊坊市·八年级期末)如图,等于( )
A.360° B.335° C.385° D.405°
4.(2020·四川省自贡市贡井区成佳中学校八年级月考)将一个五边形纸片的一个角剪去,所得多边形的内角和不可能是( )
A.180° B.360° C.540° D.720°
5.(2021·安徽阜阳市·八年级期末)如果一个多边形的内角和为,那么从这个多边形的一个顶点可以作( )条对角线.
A. B. C. D.
6.(2020·武汉市六中位育中学八年级)如图,在四边形中,,分别是两组对边延长线的交点,,分别是,的角平分线.若,,则( )
A. B. C. D.
7.(2021·山东东营市·八年级期末)如图,用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE,其中∠BAE的度数是( )
A.90° B.108° C.120° D.135°
8.(2021·河北唐山市·八年级期末)一个多边形截去一个角后,形成的另一个多边形的内角和是,则原来多边形的边数是( )
A. B. C.或 D.或或
9.(2019·莆田第十五中学八年级月考)如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请你试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=∠1+∠2 D.3∠A=2(∠1+∠2)
10.(2020·江苏无锡市·七年级期中)图1是二环三角形,S=∠A1+∠A2+…+∠A6=360,图2是二环四边形,S=∠A1+∠A2+…+∠A=720,图3是二环五边形,S=∠A1+∠A2+…+∠A=1080…聪明的同学,请你直接写出二环十边形,S=_____________度( )
A.1440 B.1800 C.2880 D.3600
二、填空题
11.(2020·浙江杭州市·八年级期末)若十二边形的每一个内角都相等,那么它每个内角的度数是____________.
12.(2021·广东汕尾市·九年级期末)如图,的度数为__________.
13.(2018·四川成都市·成都实外八年级开学考试)的两边分别垂直于的两边,且的度数比的度数的2倍少24°,则、的度数分别是____________.
14.(2020·浙江杭州市·九年级期末)如图所示,小梦发现将正六边形的边向两端延长后,可以构成 “六边星角形”,则图中的度数是_________.
15.(2021·陕西西安市·西北工业大学附属中学九年级一模)从正多边形一个顶点最多可以作7条对角线,这个正多边形每个内角的大小是_____.
16.(2020·连江县凤城中学八年级月考)如图,∠A+∠B+∠C+∠D+∠E+∠F=_______°.
17.(2021·西安市第二十三中学九年级一模)将一个正五边形和一个正六边形按如图所示的方法摆放,它们都有一边在直线l上,且有一个公共顶点O,则的度数为_________.
18.(2018·河北九年级其他模拟)将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=41°,∠2=51°,那么∠3的度数等于_____.
19.(2020·成都市金牛实验中学校七年级月考)如图,BE、CE分别为的内、外角平分线,BF、CF分别为的内、外角平分线,若,则_______度.
20.(2019·山东临沂市·八年级期中)如图,正五边形ABCDE中,对角线AC与BE相交于点F,则_______度.
三、解答题
21.(2017·山东德州市·八年级期中)如图,在五边形ABCDE中,AP平分,BP平分.
(1)五边形ABCDE的内角和为 度;
(2)若,,,求的度数.
22.(2019·云南玉溪市·八年级期中)求图中x的值.
23.(2020·海南省直辖县级行政单位·八年级期中)一个多边形的每一个外角都等于.
(1)求这个多边形的边数;
(2)求这个多边形对角线的条数.
24.(2021·全国八年级)若边形的内角和等于它外角和的倍,求边数.
已知,,为三角形三边的长,化简:.
25.(2020·内蒙古赤峰市·八年级期中)阅读材料
在平面中,我们把大于且小于的角称为优角.如果两个角相加等于,那么称这两个角互为组角,简称互组.
(1)若,互为组角,且,则______.
习惯上,我们把有一个内角大于的四边形俗称为镖形.
(2)如图,在镖形ABCD中,优角与钝角互为组角,试探索内角,,与钝角之间的数量关系,并至少用两种以上的方法说明理由.
26.(2021·黑龙江哈尔滨市·八年级期末)已知在四边形ABCD中,.
(1)如图1,若BE平分,DF平分的邻补角,请写出BE与DF的位置关系并证明;
(2)如图2,若BF、DE分别平分、的邻补角,判断DE与BF位置关系并证明;
(3)如图3,若BE、DE分别五等分、的邻补角(即),求度数.
27.(2020·安徽阜阳市·八年级期中)在中,,点D、E分别是边AC、BC(不与A、B、C重合)上的点,(P与D、E不在同一条战线上),令,,.
(1)若点P在边AB上,如图(1)且,则________°;
(2)若点P在的外部如图(2)则,,之间有何关系?
(3)若点P在边BA的延长线上运动(),直接写出,,之间的关系.
28.(2020·玉山县南山乡中学八年级月考)我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图中,的内角与的内角互为对顶角,则与为对顶三角形,根据三角形内角和定理知“对顶三角形”有如下性质:.
性质理解:如图,在“对顶三角形”与中,,,求证:;
性质应用:
①如图,则的度数为________;
②如图,在中,点,分别在,上,若比大,求的度数;
拓展提高:
如图,已知,是的角平分线,且和的平分线和相交于点,设,求的度数(用表示).
参考答案
1.A 2.B 3.C 4.A 5.C 6.D 7.B 8.D 9.B 10.C
11.150° 12. 13.,或 14.60°
15.144° 16.360 17.84° 18.10° 19.13 20.72.
21.(1)540;(2)65°
【详解】
解:(1)五边形ABCDE的内角和为,
(2)∵在五边形ABCDE中,,
,,
∴,
∵AP平分,BP平分,
∴,,
∴,
∴.
22.(1)70°;(2)100°
【详解】
解:(1)由三角形外角等于与它不相邻的两个内角的和,得x+65=x+x-5,
解得:x=70°,
(2)由四边形内角和等于360°,得x+x+10°+60°+90°=360°
解得:x=100°.
23.(1)12;(2)54
【详解】
解:(1),
答:这个多边形的边数为;
(2)(条).
答:这个多边形的对角线的条数是条.
24.8;.
【详解】
解:由题意得:,
解得:.
∵,,为三角形三边的长,
∴,,
∴.
25.(1)225°;(2)钝角∠BCD=∠A+∠B+∠D,理由见解析.
【详解】
解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°-∠1=225°,
故答案为:225°;
(2)钝角∠BCD=∠A+∠B+∠D.
理由如下:
理由①:∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360°?,
∴钝角∠BCD=∠A+∠B+∠D;
理由②:如下图,连接AC并延长,
∵∠BAC+∠B=∠BCE,∠DAC+∠D=∠DCE(三角形外角的性质),
∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D.
26.(1),证明见解析;(2),证明见解析;(3)54°
【详解】
(1).
证明:延长BE、FD交于G.在四边形ABCD中,
,,
.
,.
平分,DF平分,
,,
,
∵∠ABE+∠AEB=90°,∠AEB=∠DEG,∠FDN=∠EDG,
∴∠DEG+∠EDG=90°,
∴∠EGD=90°,即BE⊥DF.
(2).
证明:连接DB.
,.
又,.
、DF平分、的邻补角,
,,
.
在中,
,
,
,.
(3)延长DC交BE于H.由(1)得:
.
、DE分别五等分、的邻补角,
,
由三角形的外角性质得,
,,
,
.
27.(1)120;(2)∠2-∠1=∠α-80°;(3)∠2-∠1=∠α+80°或∠2-∠1=80°-∠α
【详解】
解:(1)∵∠CEP=180°-∠2,∠CDP=180°-∠1,
∴180°-∠2+180°-∠1+∠α+80°=360°,
即∠1+∠2=80°+∠α,
∵α=40°,
∴∠1+∠2=120°.
故答案为:120.
(2)根据三角形外角的性质可知,
∠2-∠α=∠1-80°,
则∠2-∠1=∠α-80°.
(3)①如图3,
∠2=80°+∠1+∠α,
则∠2-∠1=∠α+80°;
②如图4,
∠1=∠α+∠DFP=∠α+∠CFE,
∠2=80°+∠CFE,
∴∠1=∠α+∠2-80°,
即∠2-∠1=80°-∠α.
28.(1)见解析;(2)①180°;②100°;(3)
【详解】
(1)证明:据题意,得,
∴,
∵,,
∴;
(2)解:①
;
故答案为:;
②由题意得,
由(1)得,
∴,
∵,
∴,
故,
∵,
∴,
∴,
∵,
∴;
(3)解:,
理由如下:
∵和的平分线和相交于点,
∴,,
由(1)得①,
②,
由①②得,
∴,
即,
∴.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
