重庆市黔江新华高中2021届高三下学期3月第二次联合考试数学试题 Word版含答案
文档属性
| 名称 | 重庆市黔江新华高中2021届高三下学期3月第二次联合考试数学试题 Word版含答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览
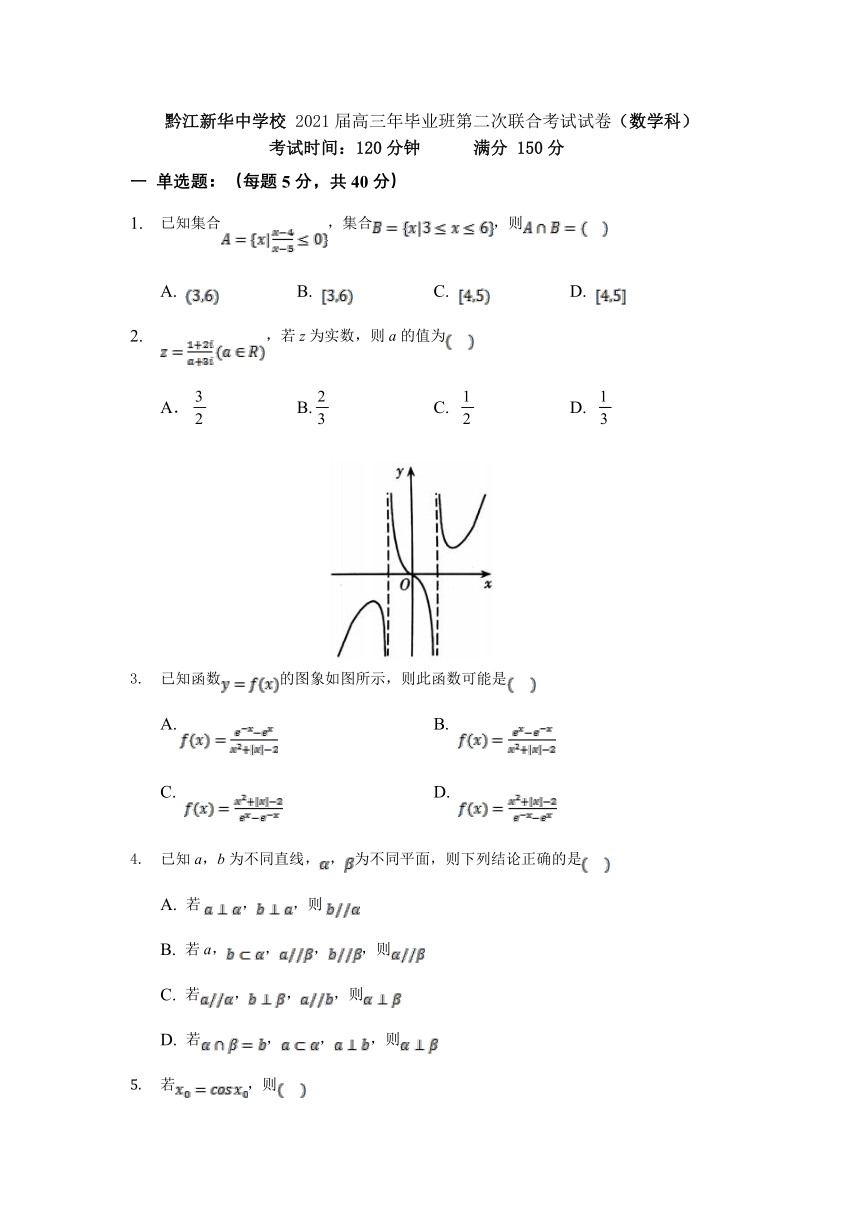




文档简介
黔江新华中学校 2021届高三年毕业班第二次联合考试试卷(数学科)
考试时间:120分钟 满分 150分
一 单选题:(每题5分,共40分)
已知集合,集合,则
A. B. C. D.
,若z为实数,则a的值为
A. B. C. D.
已知函数的图象如图所示,则此函数可能是
A. B.
C. D.
已知a,b为不同直线,,为不同平面,则下列结论正确的是
A. 若?,,则?
B. 若a,,,,则
C. 若,,,则
D. 若,,,则
若,则
A. B. C. D.
从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中恰有1名男同学和1名女同学的概率为
A. B. C. D.
已知球O表面上的四点A,B,C,P满足,若四面体PABC体积的最大值为,则球O的表面积为?
A. B. C. D.
设,为双曲线的左右焦点,点为双曲线上的一点,若的重心和内心的连线与x轴垂直,则双曲线的离心率为
A. B. C. D.
二 多选题(每题5分,漏选得2分,选错0分。共20分)
给出下列四个关于圆锥曲线的命题,真命题的有
A. 设A,B为两个定点,k为非零常数,,则动点P的轨迹为双曲线
B. 过定圆C上一定点A作圆的动弦AB,则弦AB的中点P的轨迹为椭圆
C. 方程的两根可分别作为椭圆和双曲线的离心率
D. 双曲线与椭圆有相同的焦点
在长方体中,,,,以D为原点,以,,分别为x轴,y轴,z轴正方向建立空间直角坐标系,则下列说法正确的是
A. B. 异面直线与所成角的余弦值为
C. 平面的一个法向量为 D. 二面角的余弦值为
已知a>0,b>0,则下列结论正确的是
A.若 B.若
C.若则 D.若,则
已知函数,则下列结论正确的是
A. 函数f??x??在?0,?上单调递减
B. 函数f??x??在上有极小值
C. 方程f??x?在上只有一个实根
D. 方程在上有两个实根
三 填空题(每题5分,共20分)
在的展开式中,的系数是______.
如果圆上总存在两个点到原点的距离为1,则实数a的取值范围是______ .
若数列满足:,则称数列为斐波那契数列.斐波那契螺旋线是根据斐波那契数列画出来的螺旋曲线,如图1中的实线部分(正方形内的数字与为所在正方形的边长,每个正方形中的曲线与正方形的两边构成圆心角为90°的扇形).自然界中存在许多这样的图案,比如向日葵种子的排列、芦荟叶子的排列等(如图2).若一母线长为16的圆锥的底面周长恰好等于图1的螺旋曲线的长度,则该圆锥的侧面积为___________.
函数在上不单调,则实数a的取值范围是______.
四 解答题(共70分)
(10分)已知是递增的等比数列,,,,成等差数列.
求数列的通项公式;
设数列满足,,求数列的前n项和.
(12分)某校在圆心角为直角,半径为1km的扇形区域内进行野外生存训练,在相距1km的A,B在弧上两个位置分别有300,100名学生,在道路OB上设置集合点D,要求所有学生沿最短路径到D点集合,记所有学生行进的总路程为.
设,写出S关于的函数表达式;
当S最小时,集合地点D离点A多远?
(12分)如图,三棱柱的底面是边长为2的正三角形,侧面底面ABC,且侧面为菱形,,E是的中点,F是与的交点.
求证:底面ABC;
求BC与平面所成角的正弦值.
(12分)已知椭圆焦点在x轴上过点,且离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)为椭圆的左、右顶点,直线与轴交于点,点是椭圆上异于的动点,直线分别交直线于两点.证明:恒为定值.
(12分)有一大批产品,其验收方案如下,先做第一次检验:从中任取8件,经检验都为优质品时接受这批产品,若优质品数小于6件则拒收;否则做第二次检验,其做法是从产品中再另任取3件,逐一检验,若检测过程中检测出非优质品就要终止检验且拒收这批产品,否则继续产品检测,且仅当这3件产品都为优质品时接受这批产品,若产品的优质品率为且各件产品是否为优质品相互独立.
记X为第一次检验的8件产品中优质品的件数,求X的期望与方差;
求这批产品被接受的概率;
若第一次检測费用固定为1000元,第二次检测费用为每件产品100元,记Y为整个产品检验过程中的总费用,求Y的分布列
附:,,,,
(12分)设函数,.
若,求曲线在处的切线方程;
当时,求函数的最小值;
已知,且对任意的,都有,求实数a的取值范围.
2021届高三年毕业班第二次联合考试试卷(数学科)答案
考试时间:120分钟 满分 150分
题目 1 2 3 4 5 6 7 8 9 10 11 12
答案 C A B C C C A A CD ACD ACD ABD
13.80 14. 15. 16.
17.【答案】解:设等比数列的公比为,
因为,,成等差数列,所以,
即,即,解得或舍去.
又因为,所以,所以.(4分)
由条件及可得.
因为,所以,
所以,(6分)
所以
.(8分)
又因为满足上式,所以
所以.(10分)
18. 【答案】解:中,,,
由正弦定理得,
解得,,且;
,其中;(6分)
令,
则,
当时,,y单调递减;
当时,,y单调递增;
当且仅当时,y取得最小值为;
此时,
即时,S取得最小值为;
答:当D、A的距离为时,S取得最小值为.(12分)
19. 【答案】解:证法一:取的中点M,连接EM,FM,
是与的交点,且侧面是菱形,
是的中点,,
底面ABC,底面ABC,底面ABC,
,,E为中点,,,
四边形BCME为平行四边形,,
底面ABC,底面ABC,
底面ABC,
,平面EFM,平面EFM,
平面底面ABC,
平面EFM,底面ABC.
证法二:取AC中点O,连接OB,OF,
是与的交点,且侧面为菱形,是的中点,
,,
是的中点,,,
是的中点,,,
,,
四边形OBEF是平行四边形,,
又底面ABC,底面ABC,
底面ABC.(5分)
连接,侧面为菱形,,
是正三角形,,
侧面底面ABC,侧面底面,侧面,
底面ABC,
底面ABC为正三角形,O为AC的中点,,(7分)
以O为坐标原点,分别以OB,OC,OA所在直线为x,y,z轴,建立空间直角坐标系,
底面ABC是边长为2的正三角形,
,0,,1,,0,,
1,,1,,1,,
设平面的一个法向量为y,,
由,取,得,(10分)
与平面所成角的正弦值为:
.(12分)
20【答案】(Ⅰ)解:由题意可知,,,
解得. …………3分
所以椭圆的方程为. …………4分
(Ⅱ)证明:由(Ⅰ)可知,,.设,依题意,
于是直线的方程为,令,则.
即. …………6分
又直线的方程为,令,则,
即. …………8分
所以 ,………10分
又在上,所以,即,代入上式,
得,所以为定值. ……12分
21【答案】解:产品的优质品率为,从中任取8件,X为第一次检验的8件产品中优质品的件数,
依题意有,
的期望为:,
X的方差为:.(4分)
产品被接受的概率:
.(7分)
的取值为:1000元、1100元、1200元、1300元.
,
,
,
,
的分布列为:
Y 1000 1100 1200 1300
P
(12分)
22.【答案】解:当时,,则当时,,
所以,,
则在处的切线方程为:,即;(3分)
当时,,则,
所以在上单调递增,所以;
当时,,则,
所以在上单调递增,所以;
当时,,
由可知,函数在上单调递减,在单调递增,
所以,
综上:当时,;当时,,当时,;(7分)
当时,且对任意的,都有,
即对任意有,
设,则,,
设,因为,,所以,
所以在上单调递增,
所以,即,
当即时,恒成立,所以在上单调递增,此时满足题意;
当即时,因为,且在上单调递增,所以存在唯一的,使得,
因此当时,,当时,,
所以在单调递减,上单调递增,
所以,不满足题意,
综上,.(12分)
考试时间:120分钟 满分 150分
一 单选题:(每题5分,共40分)
已知集合,集合,则
A. B. C. D.
,若z为实数,则a的值为
A. B. C. D.
已知函数的图象如图所示,则此函数可能是
A. B.
C. D.
已知a,b为不同直线,,为不同平面,则下列结论正确的是
A. 若?,,则?
B. 若a,,,,则
C. 若,,,则
D. 若,,,则
若,则
A. B. C. D.
从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中恰有1名男同学和1名女同学的概率为
A. B. C. D.
已知球O表面上的四点A,B,C,P满足,若四面体PABC体积的最大值为,则球O的表面积为?
A. B. C. D.
设,为双曲线的左右焦点,点为双曲线上的一点,若的重心和内心的连线与x轴垂直,则双曲线的离心率为
A. B. C. D.
二 多选题(每题5分,漏选得2分,选错0分。共20分)
给出下列四个关于圆锥曲线的命题,真命题的有
A. 设A,B为两个定点,k为非零常数,,则动点P的轨迹为双曲线
B. 过定圆C上一定点A作圆的动弦AB,则弦AB的中点P的轨迹为椭圆
C. 方程的两根可分别作为椭圆和双曲线的离心率
D. 双曲线与椭圆有相同的焦点
在长方体中,,,,以D为原点,以,,分别为x轴,y轴,z轴正方向建立空间直角坐标系,则下列说法正确的是
A. B. 异面直线与所成角的余弦值为
C. 平面的一个法向量为 D. 二面角的余弦值为
已知a>0,b>0,则下列结论正确的是
A.若 B.若
C.若则 D.若,则
已知函数,则下列结论正确的是
A. 函数f??x??在?0,?上单调递减
B. 函数f??x??在上有极小值
C. 方程f??x?在上只有一个实根
D. 方程在上有两个实根
三 填空题(每题5分,共20分)
在的展开式中,的系数是______.
如果圆上总存在两个点到原点的距离为1,则实数a的取值范围是______ .
若数列满足:,则称数列为斐波那契数列.斐波那契螺旋线是根据斐波那契数列画出来的螺旋曲线,如图1中的实线部分(正方形内的数字与为所在正方形的边长,每个正方形中的曲线与正方形的两边构成圆心角为90°的扇形).自然界中存在许多这样的图案,比如向日葵种子的排列、芦荟叶子的排列等(如图2).若一母线长为16的圆锥的底面周长恰好等于图1的螺旋曲线的长度,则该圆锥的侧面积为___________.
函数在上不单调,则实数a的取值范围是______.
四 解答题(共70分)
(10分)已知是递增的等比数列,,,,成等差数列.
求数列的通项公式;
设数列满足,,求数列的前n项和.
(12分)某校在圆心角为直角,半径为1km的扇形区域内进行野外生存训练,在相距1km的A,B在弧上两个位置分别有300,100名学生,在道路OB上设置集合点D,要求所有学生沿最短路径到D点集合,记所有学生行进的总路程为.
设,写出S关于的函数表达式;
当S最小时,集合地点D离点A多远?
(12分)如图,三棱柱的底面是边长为2的正三角形,侧面底面ABC,且侧面为菱形,,E是的中点,F是与的交点.
求证:底面ABC;
求BC与平面所成角的正弦值.
(12分)已知椭圆焦点在x轴上过点,且离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)为椭圆的左、右顶点,直线与轴交于点,点是椭圆上异于的动点,直线分别交直线于两点.证明:恒为定值.
(12分)有一大批产品,其验收方案如下,先做第一次检验:从中任取8件,经检验都为优质品时接受这批产品,若优质品数小于6件则拒收;否则做第二次检验,其做法是从产品中再另任取3件,逐一检验,若检测过程中检测出非优质品就要终止检验且拒收这批产品,否则继续产品检测,且仅当这3件产品都为优质品时接受这批产品,若产品的优质品率为且各件产品是否为优质品相互独立.
记X为第一次检验的8件产品中优质品的件数,求X的期望与方差;
求这批产品被接受的概率;
若第一次检測费用固定为1000元,第二次检测费用为每件产品100元,记Y为整个产品检验过程中的总费用,求Y的分布列
附:,,,,
(12分)设函数,.
若,求曲线在处的切线方程;
当时,求函数的最小值;
已知,且对任意的,都有,求实数a的取值范围.
2021届高三年毕业班第二次联合考试试卷(数学科)答案
考试时间:120分钟 满分 150分
题目 1 2 3 4 5 6 7 8 9 10 11 12
答案 C A B C C C A A CD ACD ACD ABD
13.80 14. 15. 16.
17.【答案】解:设等比数列的公比为,
因为,,成等差数列,所以,
即,即,解得或舍去.
又因为,所以,所以.(4分)
由条件及可得.
因为,所以,
所以,(6分)
所以
.(8分)
又因为满足上式,所以
所以.(10分)
18. 【答案】解:中,,,
由正弦定理得,
解得,,且;
,其中;(6分)
令,
则,
当时,,y单调递减;
当时,,y单调递增;
当且仅当时,y取得最小值为;
此时,
即时,S取得最小值为;
答:当D、A的距离为时,S取得最小值为.(12分)
19. 【答案】解:证法一:取的中点M,连接EM,FM,
是与的交点,且侧面是菱形,
是的中点,,
底面ABC,底面ABC,底面ABC,
,,E为中点,,,
四边形BCME为平行四边形,,
底面ABC,底面ABC,
底面ABC,
,平面EFM,平面EFM,
平面底面ABC,
平面EFM,底面ABC.
证法二:取AC中点O,连接OB,OF,
是与的交点,且侧面为菱形,是的中点,
,,
是的中点,,,
是的中点,,,
,,
四边形OBEF是平行四边形,,
又底面ABC,底面ABC,
底面ABC.(5分)
连接,侧面为菱形,,
是正三角形,,
侧面底面ABC,侧面底面,侧面,
底面ABC,
底面ABC为正三角形,O为AC的中点,,(7分)
以O为坐标原点,分别以OB,OC,OA所在直线为x,y,z轴,建立空间直角坐标系,
底面ABC是边长为2的正三角形,
,0,,1,,0,,
1,,1,,1,,
设平面的一个法向量为y,,
由,取,得,(10分)
与平面所成角的正弦值为:
.(12分)
20【答案】(Ⅰ)解:由题意可知,,,
解得. …………3分
所以椭圆的方程为. …………4分
(Ⅱ)证明:由(Ⅰ)可知,,.设,依题意,
于是直线的方程为,令,则.
即. …………6分
又直线的方程为,令,则,
即. …………8分
所以 ,………10分
又在上,所以,即,代入上式,
得,所以为定值. ……12分
21【答案】解:产品的优质品率为,从中任取8件,X为第一次检验的8件产品中优质品的件数,
依题意有,
的期望为:,
X的方差为:.(4分)
产品被接受的概率:
.(7分)
的取值为:1000元、1100元、1200元、1300元.
,
,
,
,
的分布列为:
Y 1000 1100 1200 1300
P
(12分)
22.【答案】解:当时,,则当时,,
所以,,
则在处的切线方程为:,即;(3分)
当时,,则,
所以在上单调递增,所以;
当时,,则,
所以在上单调递增,所以;
当时,,
由可知,函数在上单调递减,在单调递增,
所以,
综上:当时,;当时,,当时,;(7分)
当时,且对任意的,都有,
即对任意有,
设,则,,
设,因为,,所以,
所以在上单调递增,
所以,即,
当即时,恒成立,所以在上单调递增,此时满足题意;
当即时,因为,且在上单调递增,所以存在唯一的,使得,
因此当时,,当时,,
所以在单调递减,上单调递增,
所以,不满足题意,
综上,.(12分)
同课章节目录
