六年级数学下册课件-3.2.2 圆锥体的 体积 人教版(共82张PPT)
文档属性
| 名称 | 六年级数学下册课件-3.2.2 圆锥体的 体积 人教版(共82张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 703.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-07 00:00:00 | ||
图片预览

文档简介
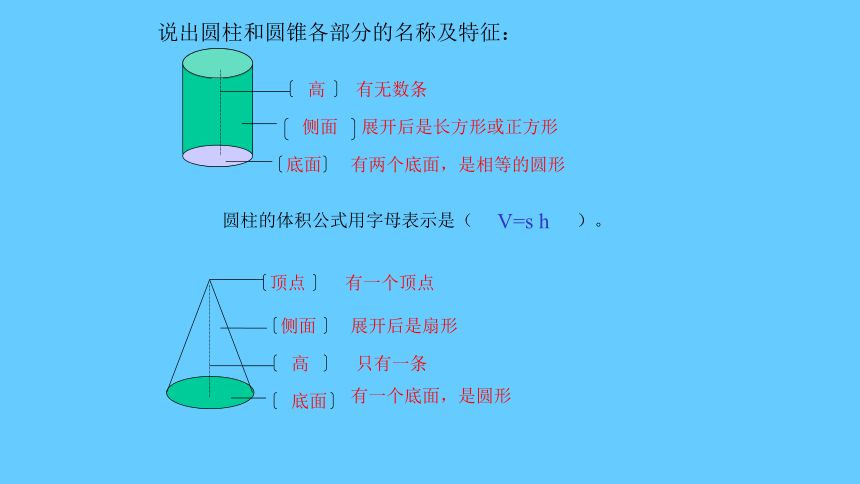
说出圆柱和圆锥各部分的名称及特征:
高
有无数条
侧面
展开后是长方形或正方形
底面
有两个底面,是相等的圆形
顶点
有一个顶点
侧面
展开后是扇形
高
只有一条
有一个底面,是圆形
圆柱的体积公式用字母表示是( )。
V=s h
底面
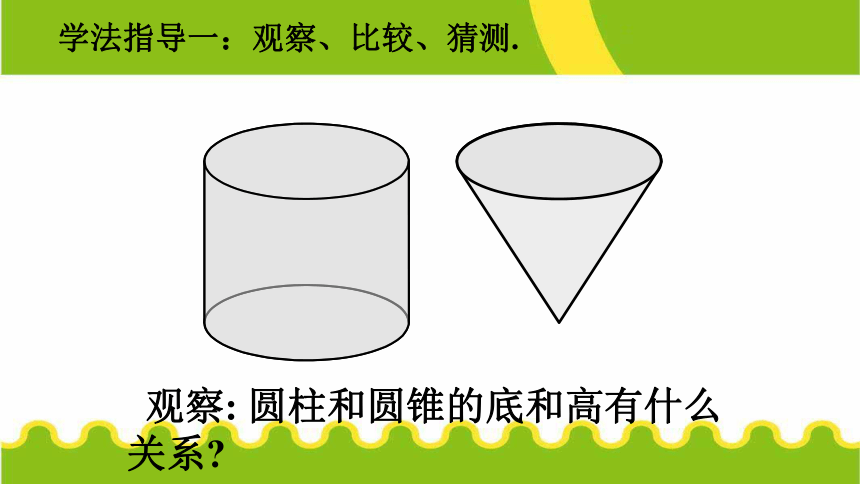
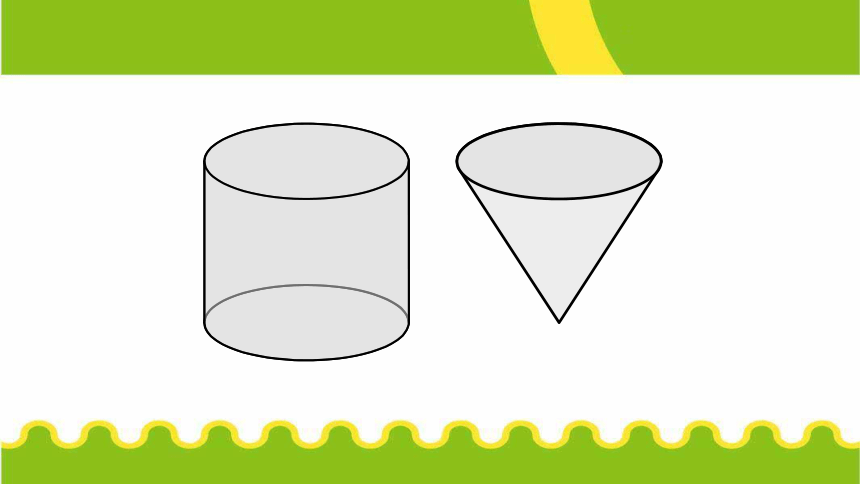
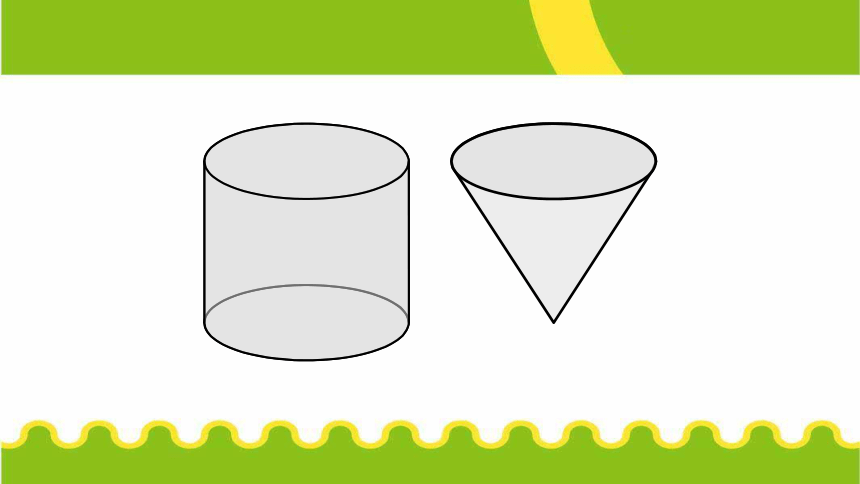
观察: 圆柱和圆锥的底和高有什么关系?
学法指导一:观察、比较、猜测.
结论:
圆柱和圆锥等底等高
圆柱和圆锥等底等高
学法指导二:实验探究圆锥与圆柱体积之间的关系.(验证)
1. 等底等高圆柱和圆锥的体积之间存在着怎样的关系?请你用自己准备的学具进行实验?
2.说说你是怎样实验的?比比谁的发现现最多?
3. 你会求圆锥的体积吗?能用一个公式表示出来吗?
同学们再看老师带给大家的实验操作,进一步证明圆柱与圆锥体积的关系,从而得出圆锥体积的计算公式。
1次
2次
3次
你发现了什么?
圆柱的体积是它等底等高圆锥体积的3倍.
圆锥的体积是它等底等高圆柱体积的
圆柱体积
1
3
圆锥体积
圆锥体积=
圆柱体积=
底面积×高
底面积 高
1
3
V圆锥=
s×h
1
3
V圆锥=
S h
=
×
学法指导三:
应用圆锥的体积公式解决实际问题及巩固练习。
例1:一个圆锥的零件,底面积是19平方厘米,高是12厘米。这个零件的体积是多少?
运用所学知识解决实际问题:
答:这个零件体积是76立方厘米。
×19 ×12=76(立方厘米)
运用所学知识解决实际问题:
例2、在打谷场上,有一个近似于圆锥的小麦堆,测得底面直径是4米,高是1.2米。每立方米小麦约重735千克,这堆小麦约有多少千克?(得数保留整千克)
1.2米
4米
想一想、议一议、说一说:
1、已知圆锥的底面半径r和高h,如 何求体积V?
2、已知圆锥的底面直径d和高h,如何求体积V?
3、已知圆锥的底面周长C和高h,如何求体积V?
r= d÷2
S=∏
V= S h
S=∏
V= S h
r =C÷∏÷2
S=∏
V= S h
三、填表:
已 知 条 件
体积
圆锥底面半径2厘米,高9厘米
圆锥底面直径6厘米,高3厘米
圆锥底面周长6.28分米,高6分米
37.68立方厘米
28.26立方厘米
6.28立方分米
看谁最细心
二、判断:
1、圆柱体的体积一定比圆锥体的体积大( )
2、圆锥的体积等于和它等底等高的圆柱体的 。 ( )
3、正方体、长方体、圆锥体的体积都等于底面积×高。 ( )
4、等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那么圆锥的体积是9立方米( )
√
×
√
×
考考你:
有一根底面直径是6厘米,长是15厘米的圆柱形钢材,要把它削成与它等底等高的圆锥形零件。要削去钢材多少立方厘米?
15厘米
6厘米
谢谢大家!
高
有无数条
侧面
展开后是长方形或正方形
底面
有两个底面,是相等的圆形
顶点
有一个顶点
侧面
展开后是扇形
高
只有一条
有一个底面,是圆形
圆柱的体积公式用字母表示是( )。
V=s h
底面
观察: 圆柱和圆锥的底和高有什么关系?
学法指导一:观察、比较、猜测.
结论:
圆柱和圆锥等底等高
圆柱和圆锥等底等高
学法指导二:实验探究圆锥与圆柱体积之间的关系.(验证)
1. 等底等高圆柱和圆锥的体积之间存在着怎样的关系?请你用自己准备的学具进行实验?
2.说说你是怎样实验的?比比谁的发现现最多?
3. 你会求圆锥的体积吗?能用一个公式表示出来吗?
同学们再看老师带给大家的实验操作,进一步证明圆柱与圆锥体积的关系,从而得出圆锥体积的计算公式。
1次
2次
3次
你发现了什么?
圆柱的体积是它等底等高圆锥体积的3倍.
圆锥的体积是它等底等高圆柱体积的
圆柱体积
1
3
圆锥体积
圆锥体积=
圆柱体积=
底面积×高
底面积 高
1
3
V圆锥=
s×h
1
3
V圆锥=
S h
=
×
学法指导三:
应用圆锥的体积公式解决实际问题及巩固练习。
例1:一个圆锥的零件,底面积是19平方厘米,高是12厘米。这个零件的体积是多少?
运用所学知识解决实际问题:
答:这个零件体积是76立方厘米。
×19 ×12=76(立方厘米)
运用所学知识解决实际问题:
例2、在打谷场上,有一个近似于圆锥的小麦堆,测得底面直径是4米,高是1.2米。每立方米小麦约重735千克,这堆小麦约有多少千克?(得数保留整千克)
1.2米
4米
想一想、议一议、说一说:
1、已知圆锥的底面半径r和高h,如 何求体积V?
2、已知圆锥的底面直径d和高h,如何求体积V?
3、已知圆锥的底面周长C和高h,如何求体积V?
r= d÷2
S=∏
V= S h
S=∏
V= S h
r =C÷∏÷2
S=∏
V= S h
三、填表:
已 知 条 件
体积
圆锥底面半径2厘米,高9厘米
圆锥底面直径6厘米,高3厘米
圆锥底面周长6.28分米,高6分米
37.68立方厘米
28.26立方厘米
6.28立方分米
看谁最细心
二、判断:
1、圆柱体的体积一定比圆锥体的体积大( )
2、圆锥的体积等于和它等底等高的圆柱体的 。 ( )
3、正方体、长方体、圆锥体的体积都等于底面积×高。 ( )
4、等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那么圆锥的体积是9立方米( )
√
×
√
×
考考你:
有一根底面直径是6厘米,长是15厘米的圆柱形钢材,要把它削成与它等底等高的圆锥形零件。要削去钢材多少立方厘米?
15厘米
6厘米
谢谢大家!
